感应式WPT系统双T型桥补偿结构的模型分析
2018-10-22王涛鸣韩如成
王涛鸣,韩如成
(太原科技大学 电子信息工程学院,太原 030024)
目前,电力系统采用输电线路传输电能,不可避免的存在导线损耗,电晕损耗,降低供电系统的可靠性和安全性等弊端。另一方面在矿井,化工厂等特殊环境使用有线电缆容易产生电火花,进而引发致命灾害。因此,无线电能传输(Wireless Power Transfer,WPT)技术应运而生。
无线电能传输技术包括磁耦合谐振式和磁耦合感应式。在磁耦合感应式无线电能传输(MCI-WPT)系统中,有四种传统的补偿结构,分别是SS型、SP型、PS型、PP型,这四种补偿方式能达到减少功率损耗的目的[1-5]。但实现功能单一,在复杂的条件下难以达到应用目的。
目前已改进的补偿结构有LCL、LCC[6-8]、单侧T型桥等,相比于传统补偿结构,改进后可实现电压增益及效率的提升。但在应用环境中负载大小、线圈之间的距离等因素皆存在不确定性,容易造成传输线圈与接收线圈之间耦合系数随时间变化,从而产生频率偏移、输出电流电压不稳定等现象。
本文在文献[3]的基础上进行改进,采用新型T型桥补偿结构,通过建立新型补偿结构的互感耦合模型,分析系统的电压及传输功率特性,对参数配置方法进行阐述,在原边电流恒流的基础上创新性地实现副边电压增益可控。并通过仿真验证了理论的正确性。
1 新型T型桥补偿结构


图1 双T型桥MCI-WPT系统电路结构
Fig.1 Topology of double-sided T-bridge MCI-WPT system
在应用环境中两线圈之间的气隙往往很大,造成互感较小,耦合系数k值较低,这就要求电源经过整流逆变输出高频交流电,实现原副边补偿元件谐振。电源频率可达到kHz乃至MHz等级。
由于原副边皆为T型补偿结构,则该系统可以实现双向无线电能传输,即负载能接收电能,也能作为电源将电能回馈电网,起到削峰填谷的作用。
1.1 参数配置分析
副边的等效电路如图2所示,UOC为副边线圈感应电压。IS为副边线圈感应产生的高频交流电,根据法拉第电磁感应定律可知,副边电流频率与原边电流频率相同。I2为负载电流。

图2 副边等效电路
Fig.2 Equivalent circuit of secondary side
分析等效电路,副边总阻抗Z1为:

(1)
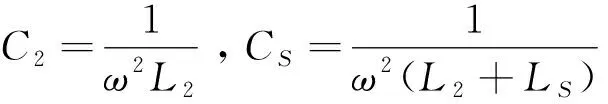
化简式(1)得:
(2)
令L2=nLs,则副边品质因数为:
(3)
当0 按以上条件配置副边补偿电容值,电容与电感相抵消,副边总阻抗等效为阻性负载,补偿元件发生谐振,电流与电压相位差为零,负载两端的阻值最大。 发生谐振时,电感电容相互抵消,电源电压完全施加于等效电阻两端,即URL=UOC. 为满足副边谐振状态,取LS为7.96 μH,CS为3.98 μF,L2为7.96 μH,C2为7.96 μF,RL为5 Ω,谐振频率f为20 kHz,负载两端的阻值与频率的变化关系如图3.电压电流相位差如图4所示。可以看到,阻值在谐振频率20 kHz附近激增,当阻值处于最高点时,相位差为零,副边总阻抗呈阻性。 图3 负载两端阻值与频率的变化关系 图4 电压电流相位差与频率的变化关系 原边等效电路如图5,Req为副边反映阻抗 (4) 图5 原边等效电路 (5) 若负载变化,传输电流不恒定容易使频率偏移,控制器失衡,所以要求图5中流经原边线圈的电流IP和图2中负载电流I2恒定,维持系统稳定。 当采用以上参数配置时,负载电流I2为: (6) (7) 由(7)式可以看出,负载电流I2与副边感应电压、补偿电容L2有关,与负载大小无关。 采用此参数配置方式可以实现负载电流的恒定,如图6所示。同理,原边传输电流IP也可实现恒定,如图7所示。图中横轴代表时间,纵轴代表电流幅值。 图6 负载电流恒流特性 图7 传输电流恒流特性 各元件参数如2.1节所述,负载变化方式设置为:0 s时负载为5 Ω,1.5/600 s时负载变为2.5 Ω,5/600 s时负载为5 Ω. 由图6图7可以看出,采用此参数配置方式可以完全实现负载电流恒流,系统稳定,有利于降低损耗。 采用此参数配置方式也可实现电压增益的控制。如图2,副边电路的输出电压增益G为: (9) 因此副边输出电压倍数与补偿电感L2LS相关,通过调节补偿电感比值n控制电压增益。因采用多组实验数据对比验证,仿真验证过程在后文第四章‘电压增益仿真验证’中阐述。 由式(7)可得,双T型桥补偿结构的输出功率为: (10) 为了验证双T型桥补偿结构的优越性,在同频率下与SS型补偿结构的传输功率作比较。传统的SS型补偿结构如图8,参数配置方式参考文献[4-6],如表1: 表1 SS型系统参数 US频率fCPLP互感/M100 V20 kHz7.96 μF7.96 μH15.98 μHCSLS负载RL电源内阻/R7.96 μF7.96 μH5 Ω0.1 Ω 图9、图10分别是双T型桥和SS型系统的输出功率,横轴代表运行时间,纵轴代表负载有功功率。可以看到改进后的补偿结构系统输出有功功率达到4 kW,而SS型系统输出有功功率为3.5 kW,表明改进后的系统可以输出更多的有功功率。有利于无线电能传输在大功率器件上的应用。 图8 Simulink中的SS型系统模型 图9 双T型桥系统输出功率 图10 SS型系统输出功率 为了验证本文所给出的电压增益和恒流特性,以及所提出的参数配置方式的正确性,根据图1在Matlab/Simulink中搭建系统仿真模型如图11. 图11 基于Simulink搭建的双T型桥MCI-WPT模型 以下给出三组仿真数据如表2,依照本文所提出的参数配置方式配置原副边补偿元件,用以验证电压增益倍数与副边补偿电感比值的关系。其中逆变桥与直流电源由100 V,20 kHz的交流电源代替。因在应用中耦合系数较小,故取k=0.2.负载恒为5 Ω.原边补偿元件参数如第2节中所述不变。 表2 三组元件参数配置 第一组第二组第三组CS3.98 μF5.3 μF2.65 μFLS7.96 μH7.96 μH7.96 μHC27.96 μF15.92 μF3.98 μFL27.96 μH3.98 μH15.92 μHn11/22 图12 三种元件参数配置输出电压波形图 如图12所示分别为三种参数配置时的输出电压波形图,第三组参数描绘的正弦曲线幅值为200 V,电压增益为2;第一组参数描绘的正弦曲线幅值为100 V,电压增益为1;第二组参数描绘的正弦曲线幅值为50 V,电压增益为0.5. 因此根据以上仿真结果,电压增益倍数完全与理论分析相符。 提出了一种新型的双T型桥补偿拓扑结构,并分别论述了其参数配置方式、负载电流恒流特性,电压增益控制方式以及相比较于SS型传输功率的优越性,并通过仿真软件验证了本文所述内容的正确性,为弱耦合应用条件下的无线电能传输装置提供了新的补偿结构应用。
Fig.3 The relationship between resistance and frequency Phase
Fig.4 The relationship between p voltage and current phase angle with frequency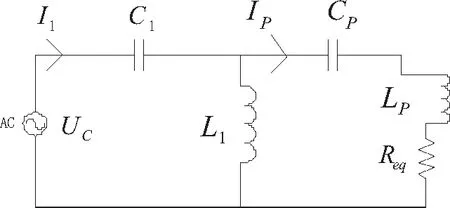
Fig.5 Equivalent circuit of primary side
2 电路模型分析
2.1 负载电流恒流特性


Fig.6 Constant current of load
Fig.7 Constant current of primary coils2.2 电压增益
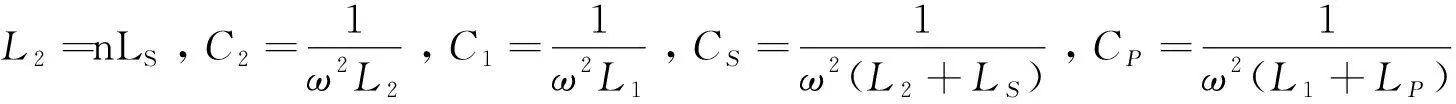
2.3 传输功率
Tab.1 Parameter of SS type system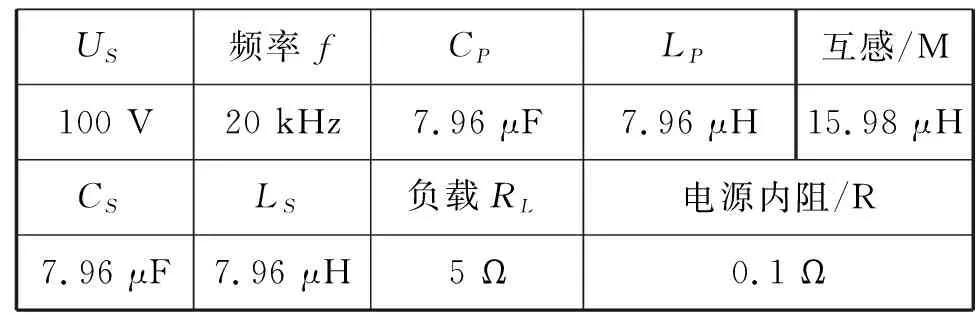

Fig.8 The Simulink model of SS type system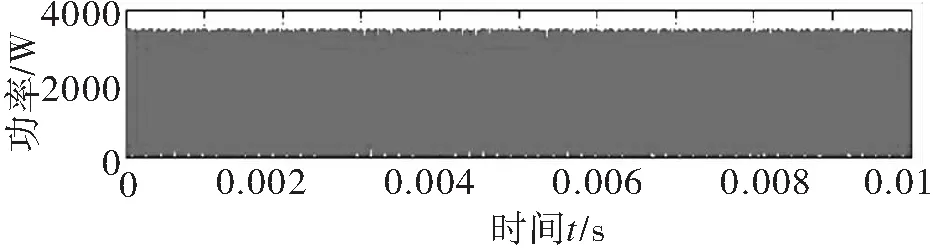
Fig.9 Output power of double-sided T-bridge system
Fig.10 Output power of SS type system3 电压增益仿真验证

Fig.11 The Simulink model of double-sided T-bridge system
Tab.2 Three groups of parameter for double-sided T-bridge system

Fig.12 Output voltage in three groups of parameters4 结论
