应用摄动有限体积法求解Navier-Stokes方程组
2018-10-22范昌胜
范昌胜,郭 强
(1,陕西广播电视大学工程管理系,西安 710119;2.西北工业大学理学院应用数学系, 西安 710072)
有限体积法(Finite Volume Method,FVM)是在上世纪八十年代末发展起来的一种新数值方法。它吸收了有限差分法(Finite Difference Method,FDM)和有限元法(Finite Element Method,FEM)的优点,是一种具有对区域剖分单元特征,能适应复杂边界,简单灵活的离散方法,同时具有间断解的适应性等优点的数值方法。但是,FVM相对FDM和FEM的弱点是精度不高[1]。国内外学者经过多年的研究,虽然发展了一些实用的有限体积格式[2-3],但这些格式的精度都不超过2阶。当求解复杂的或者局部变化比较剧烈的流动时,不超过2阶精度的格式并不能满足工程计算的需要。这就需要构造一些高精度的有限体积格式。在构造高精度有限体积格式时,关键是构造控制界面上的数值通量。数值通量构造的好坏,直接关系到格式的精度、分辨率和计算效率。目前,大多数高精度有限体积格式都是基于多基点利用高精度插值多项式来构造控制界面上的数值通量[4-5]。高智等人为克服上述缺点,提出了摄动有限体积法(Perturbational Finite Volume Method,PFVM)[6-7]。PFVM在FVM的基础上,利用对流项、扩散项之间的相互关系来提高格式精度。具体做法是,对界面质量通量的数值进行摄动,即将质量通量表示成幂级数的形式。其中,幂级数系数是由方程本身的相互关系获得的。王利业等人分别用同位和交错网格有限体积法,模拟了4:1平板收缩流动过程,并将两种方法所得模拟结果进行了吻合分析。这说明同位网格有限体积法不仅算法简洁、实现方便,结果可靠,而且容易扩展应用于非结构网格及高维问题的模拟[8]。
PFVM与FVM都是包括积分近似和插值(重构)近似的二级近似方法。与FVM 相比,PFVM由于对质量通量进行摄动而提高了插值近似的精度。在计算中,一般需要对幂级数采取截断处理。假设取幂级数的前N项作为近似,那么,以迎风有限体积方法(Upwind Finite Volume Method ,UFVM)为基础的迎风摄动有限体积方法(Upwind Perturbational Finite Volume Method ,UPFVM)就是N+ 1 阶插值近似、二阶积分近似的混合格式;以中心有限体积方法(Center Finite Volume Method ,CFVM)为基础的中心摄动有限体积法(Center Perturbational Finite Volume Method ,CPFVM)则是具有2N+2阶插值近似、二阶积分近似的混合格式。刘百仓介绍了一种基于非结构网格的二阶迎风有限体积离散格式,计算结果表明该二阶迎风有限体积算法有很好的收敛性和稳定性,且松弛因子对计算结果影响很小[9]。近年来发展起来一类新的无网格数值方法,该类方法基于点近似,不需要将节点连成单元,克服了网格类方法遇到的一些困难。由于无网格近似函数不是多项式,积分不能精确计算,一般需要用到较高阶的Gauss积分,从而增加了计算量。这样就需要包括更多的控制单元,导致求解的代数方程非常复杂,边界条件的处理也更加困难[10]。
采用PFVM和FVM计算方腔顶盖驱动流。数值结果表明,PFVM比一阶迎风、二阶中心FVM的精度和分辨率高、稳定性好。与此同时,应用PFVM计算了4:1平板收缩流,给出了不同雷诺数下的流线图、对称轴的速度图以及收缩区下游管道的速度截面图,详细分析了雷诺数对流场的影响,以及收缩区下游管道长度对流场充分发展的影响。
1 Navier-Stokes方程组的摄动有限体积格式
假设流体为二维定常不可压缩流的,则控制方程的积分形式如下:
采用基于同位网格上的PFVM离散格式求解上述方程,用动量插值解决速度和压力的失耦问题。具体计算采用SIMPLEC算法。其中UPFVM离散格式如下式(CPFVM离散格式与之类似)。
(2a)
(2b)
(2c)
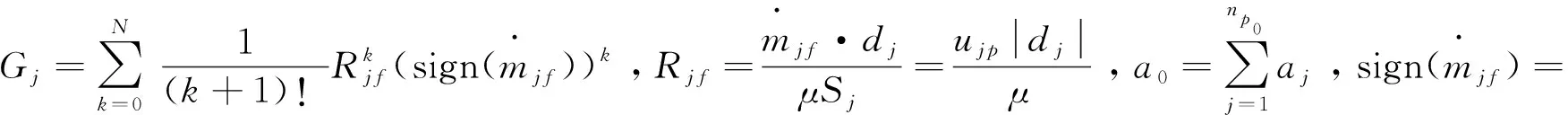

2 数值结果和讨论
2.1 方腔顶盖驱动流
为了应用PFVM求解复杂的4:1平板收缩流动,本文首先用该方法求解具有明确提法和公认基准解的方腔顶盖驱动流,以检验算法的有效性和程序的正确性。其中方腔长宽各1个单位,方腔上边界以恒定速度u=1向右运动,其它边界上的速度值为零,整个腔内流体在粘性作用下随之流动。
图1给出雷诺数Re=1 000和5 000时,用PFVM计算二维方腔顶盖驱动流的流线图。图2为Re=1 000和5 000时FVM和PFVM计算的方腔垂直中心线上u速度线和水平中心线上v速度线。在计算时,UPFVM和CPFVM的重构近似精度都取为8阶。
从图1中发现,当雷诺数较小时,左下角和右下角出现明显的一级涡。随着雷诺数的增大,右下角出现明显的二级涡,左上角出现规则的旋涡。并且原始涡的涡心位置越来越接近方腔的几何中心。在不同雷诺数下方腔中各级涡的涡心位置以及涡心处的流函数值见表1.这与文献[11]中的结果相吻合。

图1 流线图
Fig.1 Streamline diagram表1 8阶UPFVM计算的涡心位置和流函数
Tab.1 8-order UPFVM calculation of the vortex center position and stream function

Re=100Re=1000Re=5000原 始 涡流 函 数涡心位置㠹0.103420(0.6172,0.7305)㠹0.115408(0.5302,0.5603)㠹0.116057(0.5188, 0.5313)左下一级涡流 函 数涡心位置1.735×10㠹6(0.0313,0.0351)2.172×10㠹4(0.0829,0.0729)1.37×10㠹3(0.0737,0.1364)左下二级涡流 函 数涡心位置——————㠹6.0×10㠹8(0.0117,0.0078)右下一级涡流 函 数涡心位置1.248×10㠹5(0.9453,0.0664)1.786×10㠹3(0.8669,0.1131)3.0214×10㠹3(0.8229,0.0737)右下二级涡流 函 数涡心位置———㠹9.317×10㠹8(0.9922,0.0117)㠹1.98×10㠹6(0.9828,0.0204)
从图2中可以发现,在低雷诺数(Re=1 000)时,一阶UFVM的计算结果和基准解[11]的差距较大,而UPFVM和CPFVM的计算结果和基准解完全吻合。随着雷诺数增大,流场的变化越来越剧烈,控制方程的非线性也越来越强。在较高雷诺数(Re=5 000)时,一阶UFVM计算结果与基准解的差距仍是最大的。但此时UPFVM以及CPFVM的计算结果与基准解相吻合。同时,与CPFVM的结果相比,UPFVM的计算结果更好。这与文献[6]中的结论一致,它充分说明了PFVM具有高精度高分辨率的特性。
3.2 4:1平板收缩流
4:1平板收缩流能够反映流体经复杂剪切和拉伸变形后的各种特性,并且在聚合物加工过程中的挤出、注塑成型、石油的输送以及流体机械等领域有广泛的应用[12-15]。所以本文选用具有高精度高分辨率特性的PFVM来数值模拟4:1平板收缩流的流动过程以及各种物理现象。4:1平板收缩流的模拟区域如图3所示。网格划分[16]在计算中取L1=5H2,L2=12H2,H1/H2=4,其中边界条件设定如下:
(1)入口处的流速为:
(2)平板固壁采用无滑移条件,
即u=0,v=0.

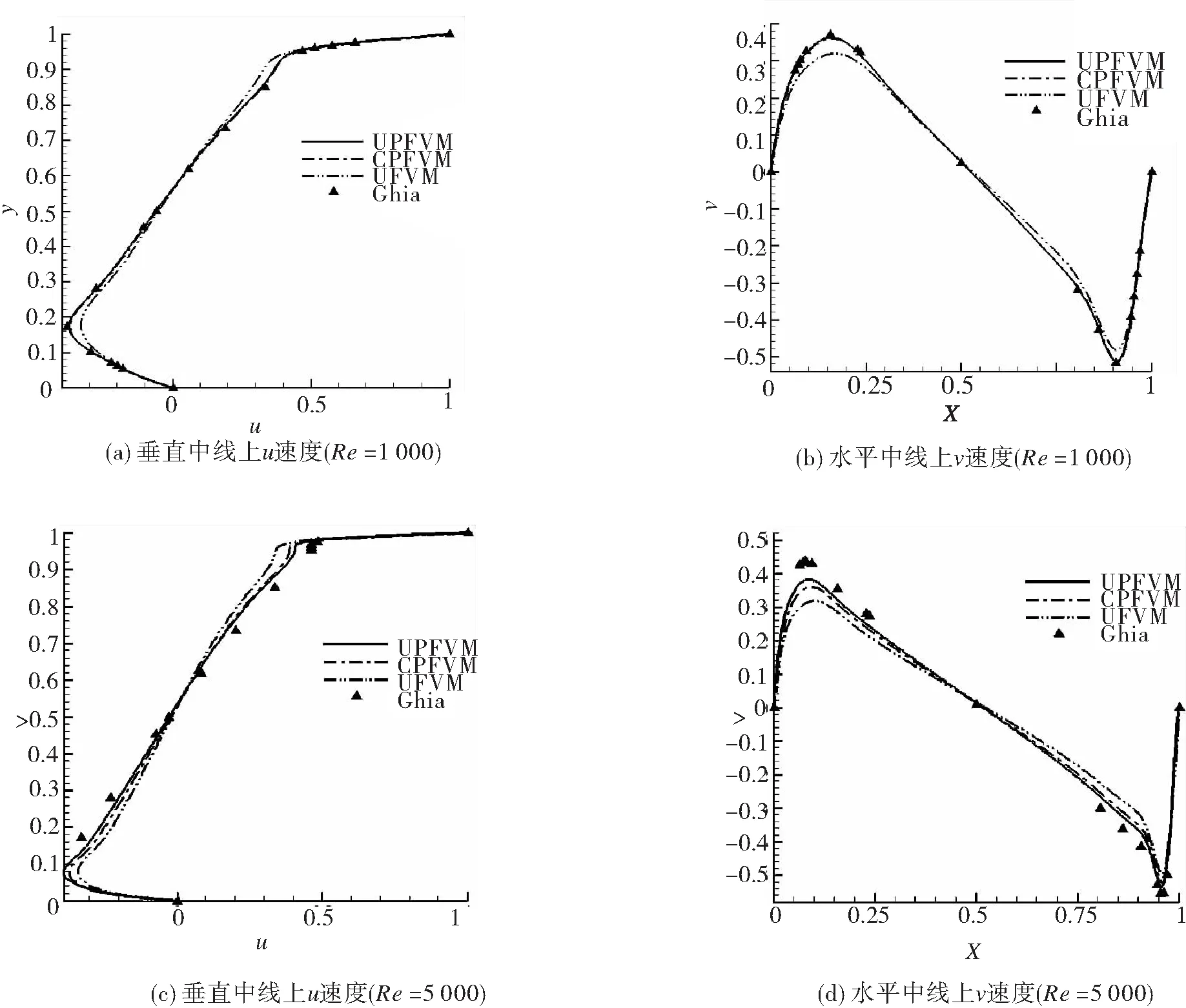
图2 中轴速度
Fig.2 Shaft speed

图3 4:1平板收缩流模拟区域示意图
Fig.3 Diagram of 4: 1 flat contraction flow simulation area
图4是不同雷诺数下,由PFVM计算的流线图。就流场流动而言,在靠近壁面且远离拐角的区域,流动以剪切为主;在接近中轴线的位置,主要是拉伸流动;而在上游拐角区域,流动更为复杂,以旋转为主;在收缩入口处,流场突然收缩,导致下游的流速增大。由图中发现,随着雷诺数的增大,回流区的主涡逐渐由竖直向水平旋转。即:在雷诺数较小时,主涡在y方向的再附着长度大于在x方向的再附着长度,但随着雷诺数的增大,主涡在y方向的再附着长度小于x方向的再附着长度。另外,主涡整体大小随着雷诺数增大而呈先减小后增大的趋势,并且当雷诺数增大到一定值时,在收缩区的下游出现一个扁长的次级涡,此涡在x、y方向的再附着长度随着雷诺数增大而增大,且在x方向增长速度比在y方向增长速度快的多。
图5是不同雷诺数下中轴线上u速度随轴向距离变化的对比图。从图5(a)中可以看出,当L2=12H2时,雷诺数Re<100时的流场已充分发展。但当雷诺数Re≥100时,流场还没有完全充分发展,这就需要将下游收缩管道长度延长。从图5(b)中发现,虽然将下游管道延长到50H2,也只有雷诺数Re=100时流场充分发展。雷诺数Re=400时流场依旧没有充分发展,直到将下游管道延长到75H2时,流场才得到充分发展。总的来说,随着雷诺数的增大,从收缩处到流场充分发展处的距离变大,并且这一变化相当剧烈。
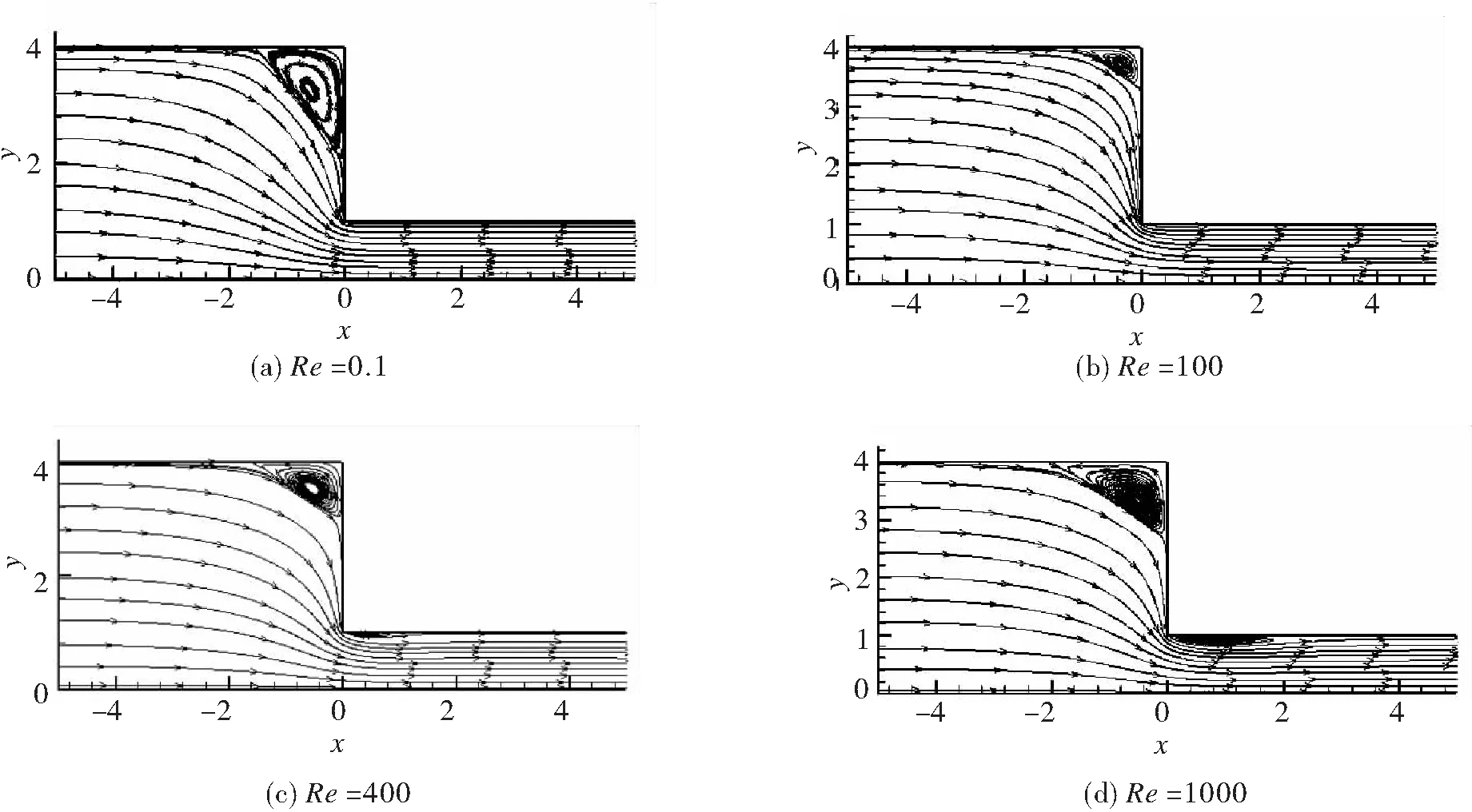
图4 流线图
Fig.4 flow chart
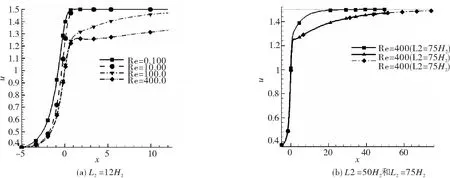
图5 中轴速度图
Fig.5 diagram of axis speed
图6是下游收缩管道不同x处截面的速度分布图。从图可以看出,当雷诺数较小时,收缩处u速度和出口处u速度相差不大,也就是说,流场在收缩处经复杂的剪切和拉伸变形后,能够在收缩管道下游很短的距离内就达到充分发展;当雷诺数较大时,收缩处u速度随y的变化非常小,只是在上板壁处有很大的梯度,并且和出口处的u速度相差也很大。同时,在收缩管道下游达到充分发展的距离也越来越大。也就是说,雷诺数较大时收缩处对流动的剪切和拉伸变形使流场发生剧烈变化,且这一变化的影响区域很大,以至于在收缩区域下游的很长距离内流场都没有达到充分发展。
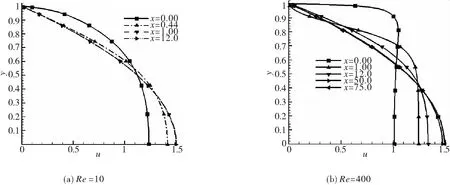
图6下游收缩管道不同横截面u速度分布
Fig.6 The velocity distribution of different cross-sections of the downstream contraction pipelines
3 结论
采用PFVM和FVM计算方腔顶盖驱动流,并且将PFVM推广到4:1平板收缩流,数值结果表明:
(1)PFVM既保留了一阶迎风、二阶中心格式基点少的优点,又具有高精度和高分辨率的特性。
(2)在4:1平板收缩流中,随着雷诺数的增大,收缩区域上游拐角的主涡呈先减小后增大的趋势。并且涡逐渐由竖直方向向水平方向旋转。
(3)在4:1平板收缩流中,当雷诺数达到一定值后,收缩区下游会出现一个扁长的涡。此涡随着雷诺数的增大而增大,并且会变的越来越“扁”。
(4)流动达到充分发展所需的收缩管道长度,随着雷诺数的增大而逐渐变长,并且变化非常剧烈。
