对异十六烷详细机理的简化研究

朱 程，方骁远，乔信起

（上海交通大学 动力机械及工程教育部重点实验室，上海 200240）

一直以来，碳氢燃料尤其是重烃燃料的化学反应动力学都是汽车发动机燃烧方向领域的一个研究重点。异十六烷是多种化石或生物衍生燃料中的异构烷烃代表性组分，是一种高度支链化的烷烃，其十六烷值仅为15，常用作构建模型燃料的十六烷值调节组分。由于异十六烷的详细反应机理规模较大，在实际的燃料化学反应系统求解中，“刚性”问题相对突出，使其在燃烧过程的数值模拟中难以直接使用。因此，对其详细化学反应机理进行简化的意义显得十分重要[1]。

目前人们对详细机理的简化方法通常是在该详细机理中提取出不重要的物质和反应，包括敏感性分析法（Sensitivity Analysis，SA）[2]、主成分分析法（Principal Component Analysis，PCA）[3]、生成速率分析法（Rate of Production Analysis，ROP）[4]、直接关系图法（Directed Relation Graph，DRG）[3]、反应路径通量分析法[5]等。还有一类方法就是在时间尺度上的简化，即基于准稳态QSS和部分平衡PE假设确认时间尺度非常小的组分和反应，以代数方程替换微分方程，降低计算的代价，包括固有低维流形法（Intrinsic Low Dimensional Manifolds，ILDM）[6]、非结构化自适应列表法[7]和计算奇异扰动法（Computational Singular Perturbation，CSP）[8]等。

很多研究表明，单一的简化方法往往不能够实现对化学反应机理的有效简化。PISTCH等[9]提出的基于误差传播的直接关系图法（DRGEP）能够快速高效地识别冗余反应机组份并删除，所以本文通过采用DRGEP法对异十六烷的详细机理进行初步简化。 ROP法可以仅从反应物或生成物反应速率的数量级上识别出机理中的次要反应，易于理解及代码化，所以在对异十六烷机理简化过程中采用ROP法删除机理中的次要组分。SA法能够对各个基元反应计算目标的重要性提供直观信息，其对机理的简化性能可靠，所以将SA法作为最后的简化方法，对主要的计算目标进行敏感性分析来剔除次要反应，保证简化达到预期规模。

简化机理一方面虽然精简了机理的规模并提高了计算效率，另一方面却在计算结果精度上造成一定损失。为了克服这一问题，人们一般以计算详细机理的结果或者试验中得到的相关试验值作为标准值，以与该标准值的最小偏差为目标，对得到的简化机理反应参数进行优化。近年来，随着计算机与智能技术的发展，智能优化算法在各领域受到很大的关注。1975年美国教授HOLLAND提出遗传算法；美国电气工程师EBERHART博士[10]和心理学家KENNEDY博士共同提出粒子群优化（PSO）算法；近几年，PERINI等[5]和董清丽等[11]利用遗传算法分别对煤油、乙醇和甲烷/空气燃烧的简化机理进行了优化。而粒子群优化作为一种基于启发式进化智能计算的优化算法，其概念简明、实现方便、收敛速度快，是一种高效的随机搜索方法。近年来，虽然该方法已经成为新的研究热点，但在化学反应动力学的应用相对比较少。本文通过合理设置PSO优化算法的自变量及目标函数对简化机理中的反应参数进行优化，使简化机理相应的计算精度大大提高。

1 异十六烷氧化简化机理构建

本文以RANZI等[12]构建的包含183组分和5 744步反应的化石及生物衍生燃料综合机理为基础，采用DRGEP识别并删除与异十六烷反应不相关的冗余反应和组分；采用ROP法删除次要组分及其对应的反应；针对ROP法对滞燃期计算带来的误差，采用PSO算法对敏感反应参数进行优化；最后对多种反应器的不同目标参数进行敏感性分析，实现对异十六烷机理的最终简化。简化过程中选取的目标参数包括激波管（Shock Tube，ST）中的滞燃期，射流搅拌反应器（Jet Stirred Reactor，JSR）中重要组分的浓度以及层流预混火焰（PREMIX）的火焰传播速度。

1.1 DRGEP法简化

在传统的DRG中，采用组分A对组分B生成率的正规化贡献rAB来表示组分A和B之间的耦合关系。2008年，PISTCH等[9]提出基于误差传播的直接关系图法重新定义了组分之间的耦合关系式：

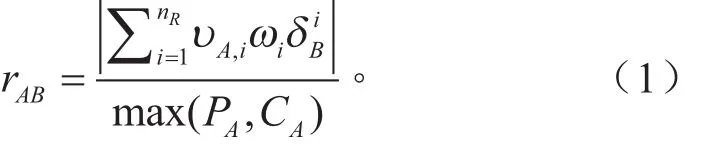
式中：

式（1）和（2）中，−υA,iω表示第i个反应下关于组分A的净化学反应计量系数，而ωi表示第i个反应的净化学反应速率。简化时，以详细机理计算的滞燃期为目标参数，采用二分法找出最佳的简化阈值，最终其被定义为7%，将iC16H34、CO2、CO、H2O、N2、O2等反应物和最终生成物设置为保留组分，得到了包含125组分2 421步的异构十六烷简化机理。图1为选取φ=1.0，p=2 026.5 kPa下覆盖750 K到2 000 K温度范围的5个工况点详细机理与简化机理计算结果的对比。

可以看出，初步简化后的机理引起滞燃期相对于目标机理的误差在自定义阈值内，5个工况下的目标参数与目标机理基本吻合，其中在750 K时的相对误差略大，表明了简化机理在低温工况下滞燃期的敏感性相对较高，更容易引起计算偏差。

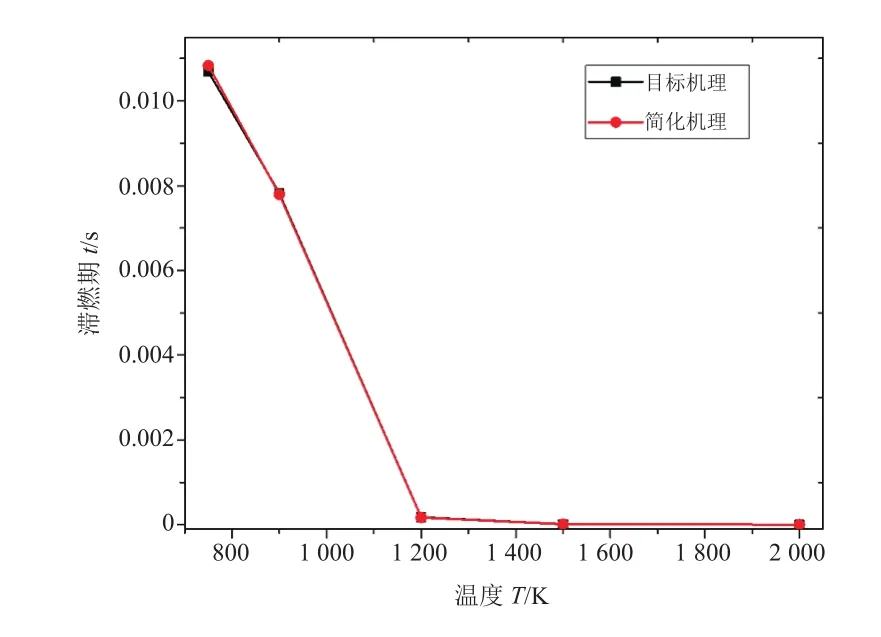
图1 DRGEP简化机理与目标机理滞燃期比较

1.2 ROP法简化

ROP法可以用来分析得到不同基元反应对反应物种生成或消耗的重要性指数，能快速找出反应系统中主要的基元反应。组分a的生成（消耗）速率pa（数值上等于净反应速率ωa），以及不同基元反应对组分a生成（消耗）速率的重要性指数E可以表示为：

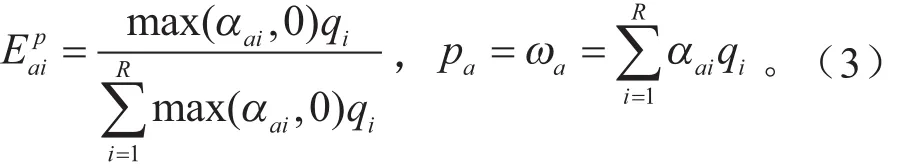
式中：αai和qi分别为第i个基元反应中的化学当量系数和反应速率；αaiqi为第i个基元反应对物种a生成（或消耗）的影响；R为反应机理系统中涉及到物种a的反应个数。ROP系数反映了当前基元反应对该物种生成的影响程度，当ROP系数为正时，表示当前基元反应促进了该物种的生成，反之则表示会促进该物种的消耗分解。

本文将组分a（a为任意分析组分）参与的所有消耗反应中最小的重要性指数设为参考值。设定阈值为ε进行简化，即当组分a参与的其它消耗反应计算的重要性指数时（其中都为负数），对应的消耗反应被视为“次要反应”，需要被删除，否则被保留在简化机理中。经过多次尝试后发现ROP阈值被设定为1%时，简化机理关于滞燃期的计算误差较小，简化结果整体较理想，仅低温区的计算误差较大。ROP阈值1%简化后的机理规模为86种组分和759步反应。

1.3 PSO算法优化反应参数

针对ROP法简化后机理在低温区存在较大误差的问题，采用粒子群优化算法对敏感反应的速率常数进行优化。本文通过对滞燃期敏感性分析选取的敏感反应为燃料高温裂解反应R1、烷基加氧生成过氧烷基的反应R15和过氧化氢酮裂解反应R19。

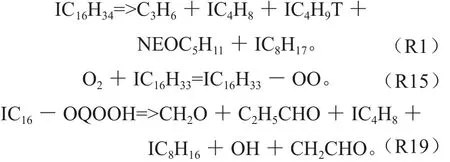
PSO是通过初始化产生多个随机粒子，经过不断迭代找到最佳粒子的过程。图2是本文采用粒子群算法的流程图，其中速度和位置信息更新公式为：

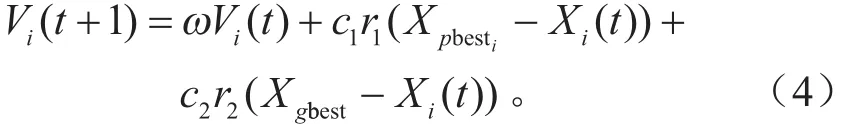
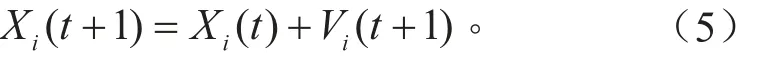
式中：Vi( t)为粒子i在第t代中的速度；Xpbesti和Xgbest分别表示粒子自身经历的历史最好位置和群体所经历的全局最好位置；设置学习因子c1= c2=2. 0，惯性权重ω=0. 4；r1和r2为服从均匀分布U[0,1]的随机数；X和V维数为N×n，N为粒子群规模大小，n为自变量粒子维度。

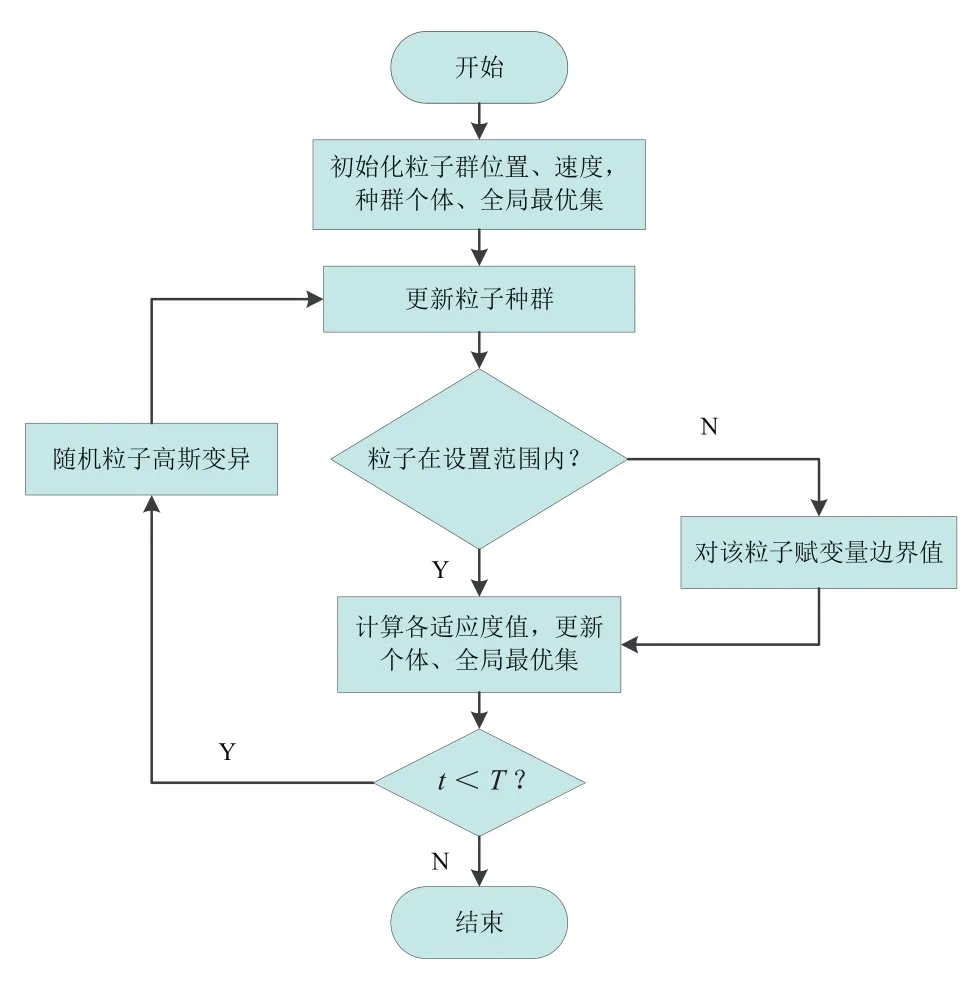
图2 粒子群优化算法流程图

本文对粒子种群的定义为X =(X1, X2,… ,XN)，对每个粒子向量Xi=(xi1, xi2,… ,xin)，粒子变量xij=K KK，其中反应速率常数K = A Tnexp ( − E / R T )，

ijIJKIJ为第i组初始变量对应的第j步反应的初始反应速率常数，Kij为优化前第i组变量对应的第j步反应的反应速率常数。设粒子变量的取值范围为[0.1,10]。

对上述粒子向量中的每个xij都能通过逆推导得出阿累尼乌斯参数Ai，Bi和Ei，从而每个粒子向量Xi=(xi1, xi2,… ,xin)都能组成n步的修改过参数的机理，利用该机理能计算出相应试验工况下的计算值。本文中目标函数定义为包含m个元素的目标向量，表达式为：

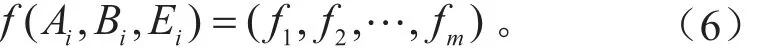
本文中随机生成了N=20组粒子，进化代数T=120，目标函数为m=9个正交工况点下的滞燃期计算结果与ROP法简化机理计算结果的偏差。优化结果见表1。

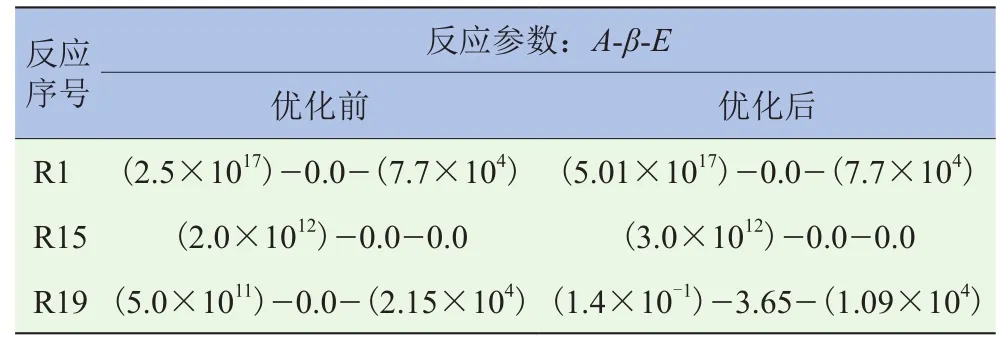
表1 粒子群对敏感反应参数的优化结果

1.4 SA法简化

上述ROP法简化后的机理规模仍然相对较大，为此采用SA分析法进一步简化。首先将机理中特定组分对应的基元反应逐个移除，并计算移除带来的误差变化：

式中：δB,ind为组分B参与的某个反应被移除后机理计算的目标参数相对原始机理的误差；δROP为使用ROP机理计算时相对原始机理的误差。随后针对组分B按照不同的δB值从大到小依次删除对应的基元反应，每移除一个反应后评估总误差，直到最大误差达到定义的误差限值。

将燃料iC16H34和燃料在反应中主路径裂解、异构、氧化和脱氢反应后的重要产物以及氧化剂O2、燃烧产物CO2、CO、H2O等参与的反应保留不作分析以节省计算时间，对其余组分逐个进行敏感性分析。目标工况为覆盖高中低3个水平下当量比、温度和压力的9个滞燃期正交工况点，阈值取该9个点的平均相对误差为11%进行删除简化，得到了187步反应的异十六烷机理。

以滞燃期为目标参数得到的187步简化机理仅对滞燃期具有较高的计算精度，并不能保证机理关于燃料其它燃烧特征的计算可靠性。因此，随后针对上一步被简化操作删除的所有反应逐个分析其对JSR中重要组分浓度及层流预混火焰传播速度的敏感性。JSR的目标工况同样为9个正交的工况点，阈值定义为平均相对误差2.1%。PREMIX由于计算网格较多，计算复杂比较难出结果，所以仅针对ωφ=1.1进行分析，并取阈值为8%。最终在原简化机理的基础上增补了112步反应，得到了83组分299步反应的异十六烷简化机理。

2 简化结果验证

2.1 ST滞燃期的验证

图3～5是基于异十六烷原综合机理和本文构建的简化机理分别在Chemkin-Pro的激波管模型中模拟得到的滞燃期随初始温度的变化，其中选取三个计算当量比ωφ=0.5、1.0、1.5，两个计算压力ωp =1 013.25 kPa、4 053 kPa，计算温度选择在700～2 000 K范围内。

图3 简化机理和详细机理在激波管中滞燃期随温度变化预测值的比较，φ=0.5

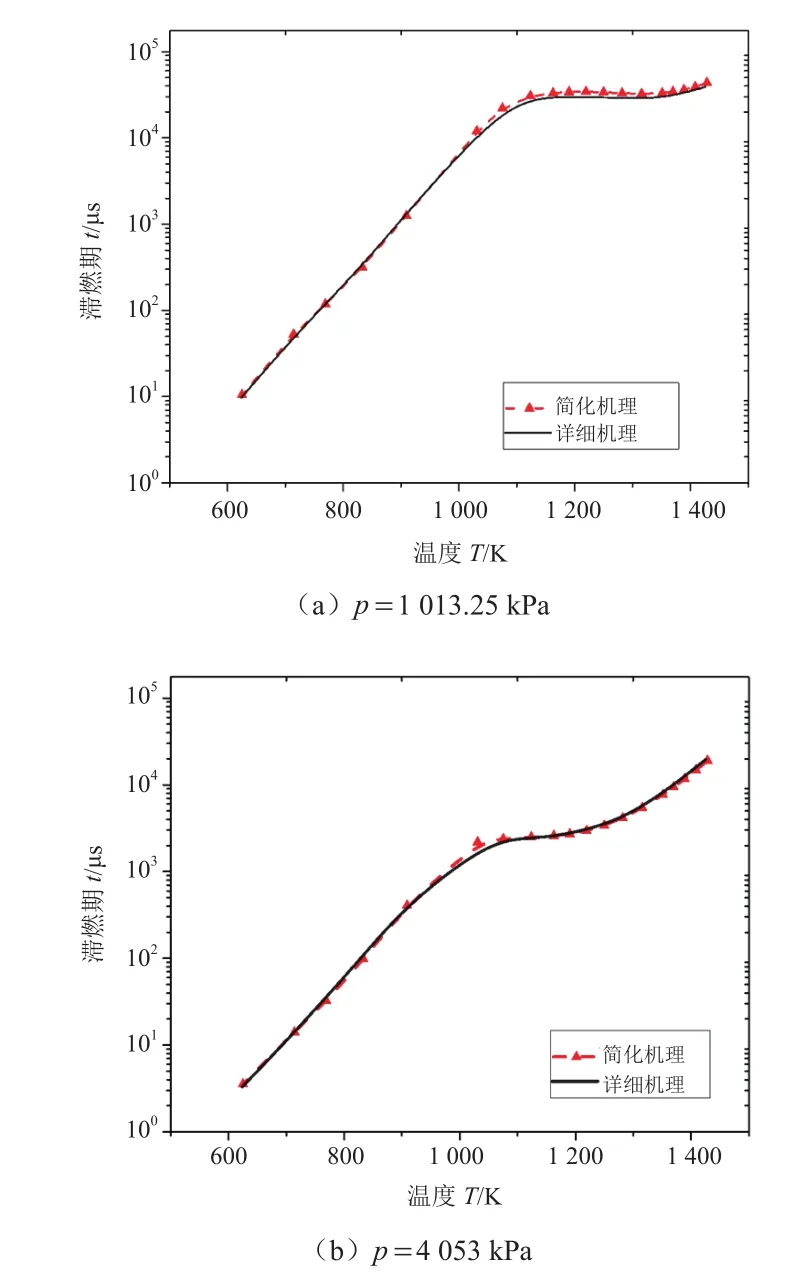
图4 简化机理和详细机理在激波管中滞燃期随温度变化预测值的比较，φ=1.0

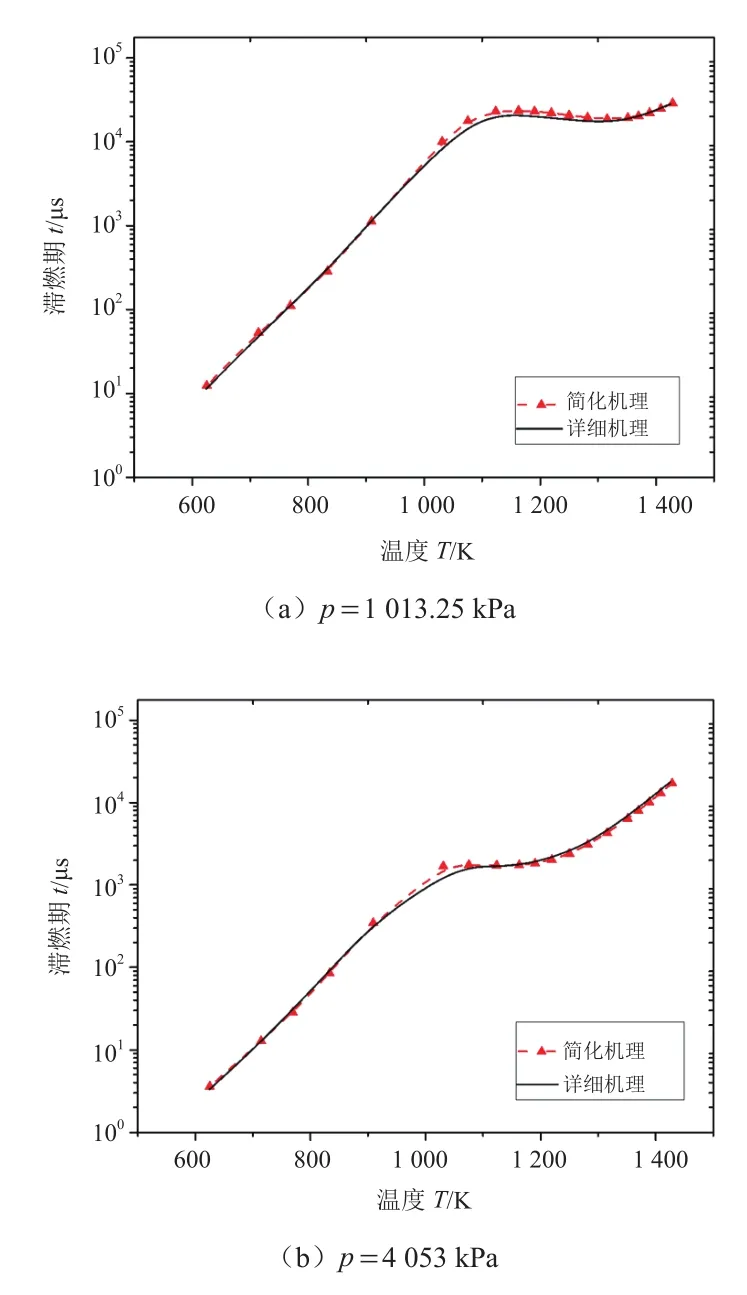
图5 简化机理和详细机理在激波管中滞燃期随温度变化预测值的比较，φ=1.5

由图3～5可知，在700～800 K和1 300～2 000 K范围内两种机理的预测值稍有偏差，其中在低温区比在高温区的误差更大。简化机理在800～1 300 K范围内与详细机理的预测值基本吻合，表明简化机理在该温度区间内的计算精度更高。在三个当量比下4 053 kPa曲线和1 013.25 kPa曲线相比，简化机理与详细机理的吻合程度都要高，表明该简化机理在高压4 053 kPa情况下的计算精度相对于低压1 013.25 kPa情况下的计算精度更高。但从整体看，简化机理与原综合机理关于滞燃期的预测结果基本一致。

2.2 JSR组分浓度的验证

采用Chemkin-Pro中常压、等温的良搅拌器模型对射流搅拌器（JSR）进行模拟，模拟工况根据DAGAUT等[13]的试验选取φ=0.5、1.0、2.0三个当量比，计算温度范围为770～1 030 K，计算压力为1 013.25 kPa。图6～8分别为在φ=0.5、1.0、2.0的情况下，基于299步简化机理和详细机理模拟计算的组分浓度随温度的变化结果，其中重点关注燃料iC16H34、氧化产物CO2/CO和H2O以及其它重要中间产物CH4、CH2O等共6种组分。从图中可以看出，简化机理和详细机理对6种组分的浓度演变过程预测误差都很小，在三种工况下两者的计算结果都很接近。

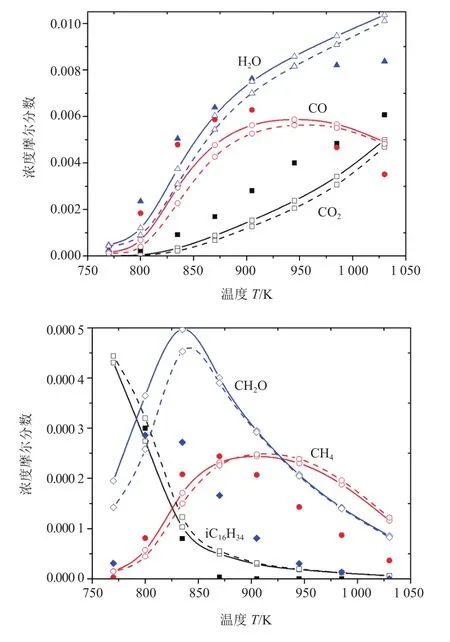
图6 JSR 中主要组分浓度的详细机理预测值（实线）、简化机理预测值（虚线）与试验值（实心符号）[16]的比较，p=1 013.25 kPa，φ=0.5

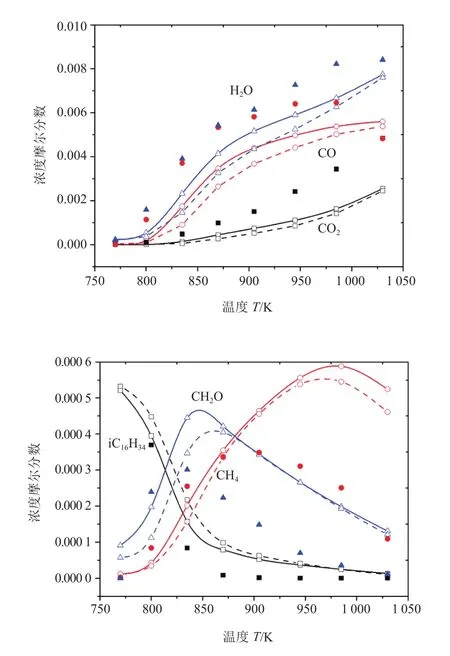
图7 JSR 中主要组分浓度的详细机理预测值（实线）、简化机理预测值（虚线）与试验值（实心符号）[13]的比较，p=1 013.25 kPa，φ=1.0

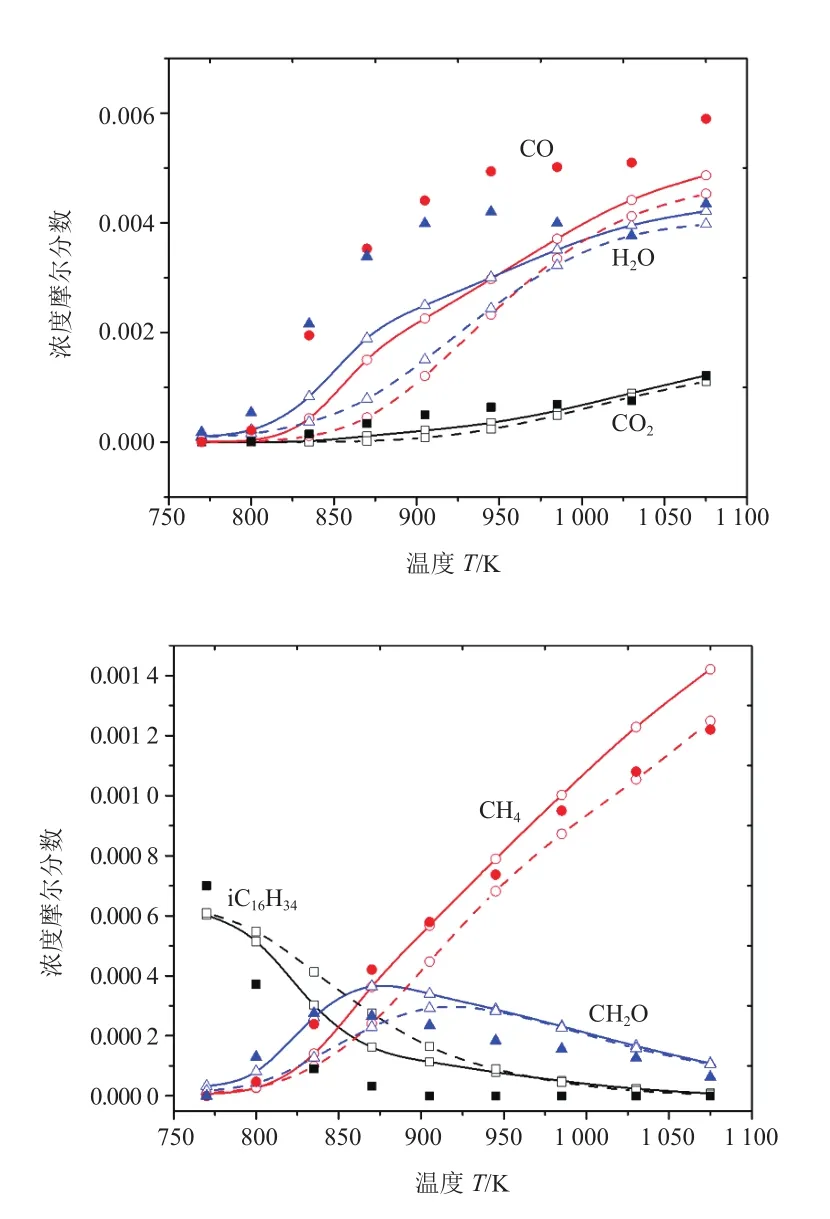
图8 JSR 中主要组分浓度的详细机理预测值（实线）、简化机理预测值（虚线）与试验值（实心符号）[13]的比较，p=1 013.25 kPa，φ=2.0

对比图6～8可知，在富氧情况下详细机理与简化机理的预测值相比其它两种工况下的吻合度要高，证明该简化机理在富氧条件下对详细机理关于重要组分浓度的计算精度损失最小。且在T=850～950 K温度区间随着当量比的增加，CO、H2O浓度的计算精度损失增大；CH2O的浓度在T＜900 K时相对详细机理的浓度计算误差最大，其次是CH4；而在高温区，其浓度随着贫氧程度增大其计算误差也增大。整体上，详细机理和简化机理在关于JSR重要组分浓度计算上较为一致，简化机理的计算相对详细机理有较高的还原度。

而在与DAGAUT等的试验数据对比上，iC16H34的吻合度最高，其次是CO、CO2、H2O等组分，且随着当量比增加，iC16H34、H2O、CO计算浓度和试验值的吻合度变差，而CH4、CO2、CH2O浓度计算值吻合度变高。总体而言，本文的简化机理对射流搅拌器组分浓度的预测是可靠的。

2.3 PREMIX层流火焰速度的验证

采用Chemkin-Pro的层流预混火焰模型，根据试验条件在未燃混合气温度Tu=443 K、压力p=101.325 kPa的情况下验证层流火焰速度随当量比的变化，图9是计算结果和试验数据的对比图，实心点符号是来自清华大学李博[14]的试验数据，虚线是简化机理的模拟曲线。可以看出，在φ=0.9到φ=1.1之间，预测值略小于试验结果，但在φ=0.8到φ=0.9以及φ=1.1到φ=1.4两段区间内，299步简化机理计算值与试验值高度一致，在φ=0.8到φ=1.4之间的平均误差小于2%，可认为简化机理的层流火焰速度预测值较为精确地反映了实际的层流火焰速度。

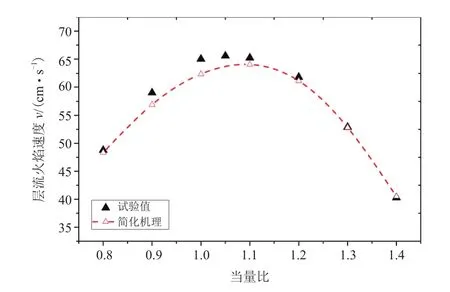
图9 火焰传播速度的预测值（虚线）与试验值[14]的比较，p=101.325 kPa，Tu = 443K

3 结论

（1）本文基于DRGEP、ROP和SA三种方法对183组分5 744步反应的综合机理进行多次简化，简化过程中采用PSO算法对简化机理反应参数进行优化使计算结果偏差达到最小，最终得到83组分299步反应的异十六烷简化机理。关于构建的异十六烷简化机理动力学文件、对机理计算时使用的热力学参数文件、传质参数文件，以及应用到的简化方法、优化算法程序，读者都可以通过访问作者GitHub主页中的iso-cetane-reduction-mechanism仓库下载参考，该仓库地址为：https://github.com/dutzhucheng/iso-cetane-reduction-mechanism。

（2）DRGEP方法对剔除冗余反应和组分的效果明显，而对标记的主要和次要组分中，ROP方法逻辑直观、结果理想，SA方法在移除次要反应过程中占主导地位，PSO优化算法能够对多反应模型计算结果偏差进行修正优化，优化效果显著。其中三种简化方法按照其简化效率从小到大的顺序进行，有效地减小了单一简化方法的不确定性和目标依赖性，所以该简化流程同样可以有效地对其它燃料尤其是重碳纯燃料组分如正十二烷等的详细机理进行简化，具有较高的普适性。

（3）在对DRGEP、ROP及SA法的阈值进行选择时，反应机理中存在相当一部分的重要反应会被过大的阈值简化，而阈值选择过小时的简化效率不高。采用二分法分别定义各简化方法的可行阈值，一方面可以减小简化过程的计算量，另一方面可以使反应机理在尽可能简洁的同时保持相关的计算精度。

（4）最终得到的异十六烷简化机理模拟的激波管滞燃期、射流搅拌反应器组分浓度和层流预混火焰速度与原机理或试验值吻合度较高，表明本文采用的简化方法及简化流程是合理可靠的。