基于小波变换与子结构法的多层剪切结构时变参数识别
2018-10-20朱宏平
王 超,朱宏平
(1.湖北工业大学 土木建筑与环境学院,武汉 430068;2.华中科技大学 土木工程与力学学院,武汉 430074)
土木工程结构模态参数和物理参数辨识是一个重要的研究课题,可以广泛应用于结构的健康监测与性能评估,损伤诊断与维修管养。当前大多数参数辨识技术针对的是线性时不变系统,然而土木工程结构在长期的运营过程中,由于结构损伤或退化,刚度与阻尼特性将随时间而发生变化,结构是时变系统。杨武等[1]提出一种前后向泛函向量时变自回归滑动平均(FS-VTARMA) 时间序列模型联合估计的模态参数辨识方法。周思达等[2]提出了基于矩阵分式多项式模型的时频域线性时变结构模态参数最小二乘辨识方法。于开平等[3]提出了一种改进的扩展卡尔曼滤波(EKF)步骤,然后将改进步骤做为人工神经网络的学习算法用于基于前向神经网络的非线性时变系统辨识。
对于时变物理参数识别问题,李会娜等[4]提出了一种基于随机激励响应信号的子空间法识别时变物理参数,通过对响应信号组成的Hankel矩阵进行奇异值分解,识别出等效状态的系统矩阵,进而识别出结构的刚度、阻尼矩阵。静大海等[5]利用子空间法实时辨识出时变结构系统的特征值与特征向量,然后以子结构法为基础在线辨识出结构系统连接处的物理参数。Xu等[6-7]提出了一种基于状态空间和小波变换的时变参数识别方法,将时变系统二阶振动微分方程转换为一阶状态方程,利用小波变换将状态方程进行解耦,识别出系统不同时刻的转移矩阵,进而识别结构的时变参数。Yang等[8-9]提出了带自适应遗忘因子在线最小二乘法识别结构的物理参数。然而对于参数突变等行为该类方法不能很好追踪其变化。Shi等[10]提出一种基于经验模式分解的方法识别时变物理参数。易伟建等[11]基于希尔伯特-黄变换的方法并采用等效思想来识别结构低阶模态的刚度时变规律。Wang等[12]利用希尔伯特变换的方法在信号时域内提取结构时变模态和物理参数。然而经验模型分解缺乏数学上的精确证明,分解也存在一些不确定性。
近年来,许多学者提出基于小波变换的时变参数识别。Tsatsanis等[13]提出采用小波基函数将时变结构时变系数展开,将时变问题转化为时不变问题进行参数识别。任宜春等[14]利用小波函数多尺度逼近法,分析了剪切型结构在地震作用下时变的阻尼和刚度识别问题。Chang等[15-16]采用小波多分辨率分析方法时变滞回结构物理参数。王超等[17-18]也研究了小波多分辨率技术对不同时变刚度与阻尼的识别,探讨了小波基选择及小波分解层数的优化问题。
然而,实际土木工程结构通常非常复杂,自由度很大,而结构损伤或时变部分通常发生在局部,上述的小波方法需要同时测量所有自由度的位移、速度与加速度,对复杂结构来说如何测试是一个很大的问题,而且自由度多了后会识别方程病态问题严重,计算耗时,抗噪性变差。
针对多层剪切时变结构,本文结合小波变换和子结构技术提出了一种时变物理参数识别方法,将局部时变的结构提取出来作为子结构,对子结构进行小波多分辨率分析识别其时变参数。采用一个多层的剪切框架结构数值模拟分析验证方法的有效性和抗噪性。
1 小波多分辨率分析
小波尺度函数φ(t)和小波函数ψ(t)通过在不同尺度进行伸缩与平移可以构成小波空间的正交基函数
(1)
(2)
式中:j为尺度参数;b为平移参数。
对于有限能量信号x(t),小波多分辨率分析在不同尺度上将信号用正交基函数分解展开为
(3)
式中:J为小波分解展开的层数;aJ,b为第J尺度的尺度系数;dj,b为第j尺度的小波系数。通过多分辨率分析可以得到信号在不同分辨率下的信息。第一项得到信号x(t)在第J尺度上的低频成分信息,第二项是信号x(t)在不同尺度j上的高频成分信息。
实际采集的通常为离散信号,当信号采样频率大于Nyquist频率时,可以将离散信号x(n)近视作为信号在0尺度分解上的尺度系数a0,b,离散形式的小波分辨率分析可以表示为
(4)
2 子结构法时变参数识别
对于图1所示的多层时变剪切型框架结构,假定已知结构在第i+1到i+s的局部s层发生时变。按照Koh等[19]提出的子结构法理论,将发生时变的s层结构当做子结构,结构其他部分对子结构的效应作为外荷载,通过交界面(本模型中交界面为第i+1层和i+s层)施加给子结构。子结构运动方程为
(5)

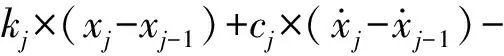
(6)
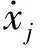
图1 多层剪切框架结构Fig.1 Electromechanical
如果结构的刚度和阻尼为时变,可以将刚度和阻尼作为待识别变量,将回复力表示成
Rs(t)=Θs(t)×γs(t)
(7)

(8)
(9)
γs(t)=[ki+1ki+2…ki+s+1ci+1ci+2…ci+s+1]T
(10)
将式(7)代入式(5)可将子结构运动方程变为
(11)
对结构响应进行离散采样,采样时刻n=1~N,则可将上式连续运动方程转变为相应的离散运动方程(连续时间变量t变为离散变量n)
(12)
由式(12)可知,对于第i+1层和i+s层共s层待识别的时变刚度和阻尼,采用子结构法时需要同时识别第i+1层和i+s+1层共s+1层参数。将待识别的时变参数的离散化结果kj(n)、cj(n)(j=i+1,i+2,…,i+s)进行小波多分辨率分析,根据式(4)进行展开。对土木工程结构,其参数通常缓慢变化,信号能量大部分集中在低频部分,为了减少待识别的参数提高识别精度,对时变参数进行多分辨率展开分析时,可截断第二项高频成分,由展开的第一项低频成分来近似描述时变阻尼和刚度
(13)
(14)
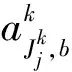
将式(13)、(14)代入式(11)可得
P(n)A≈Z(n)
(15)

(j=i+1,i+2,…,i+s+1)
(j=i+1,i+2,…,i+s+1)
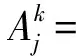
(j=i+1,i+2,…,i+s+1)

(j=i+1,i+2,…,i+s+1)
这样可以将时变参数(k(n)和c(n))识别问题转变为时不变的小波系数A求解问题,在式(15)中未知的小波系数可通过最小二乘法进行求解
A=P+Z=(PTP)-1PTZ
(16)
将求解得到的小波系数待入式(13)、(14)即可识别结构的时变阻尼和时变刚度。
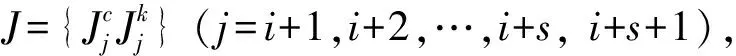
(17)
式中:N为实测响应信号长度;NA为待求解的小波系数A的个数。
3 数值验证
为验证提出方法的有效性和抗噪性能,建立一个9层剪切框架结构数值模型进行仿真分析,如图1所示。结构初始参数分别为:m1=m2= 6 000 kg,m3=m4=5 000 kg,m5=m6=m7=m8=m9=4 500 kg。k1=k2= 3×106N/m,k3=k4= 2.4×106N/m,k5=k6=k7=k8=k9= 2×106N/m,c1=c2= 5×104N·s/m,c3=c4=4×104N·s/m,c5=c6=c7=c8=c9= 3×104N·s/m。
模拟结构在4、5层局部发生时变,其中第4层刚度和阻尼线性变化,第5层刚度和阻尼三次曲线变化(刚度单位为N/m,阻尼单位为N·s/m),具体变化情况如下
(18)
(19)
(20)
(21)
模拟结构受到EI Centro地震荷载作用,采用四阶龙格库塔法数值求解结构响应。如果采用通常方法,要识别时变参数,需要同时识别整个9层结构的刚度和阻尼,各层参数的小波分解层数优化计算量非常巨大,同时识别的位置参数过多方程病态问题严重,而且需要知道每一层的结构响应。由提出的子结构法理论,只需提取结构第4~6层间的相对位移、速度和绝对加速度响应即可对时变参数进行识别。计算响应的采样频率为50 Hz,提取结构25 s响应数据进行分析。模拟计算的结构各层间相对位移和速度响应如图2和3所示。同时,为考虑方法的抗噪性,对结构响应添加5%的高斯白噪声(噪声大小定义为噪声均方根/信号均方根)。采用提出的方法对结构在不同噪音情况下的响应进行分析,识别结构的时变刚度和阻尼。

图2 各层间相对位移Fig.2 The relative displacement between different layers
根据王超等指出,具有线性等缓变的参数可以用db3小波来分析,而突变参数可以用haar小波进行分析。这里第4、5层时变刚度和阻尼采用db3小波进行多尺度展开,而第6层刚度和阻尼未发生时变,可以采用harr小波进行多尺度展开。不同噪音水平下优化后的各参数分解层数如表1所示。刚度和阻尼识别结果如图4~图9所示。
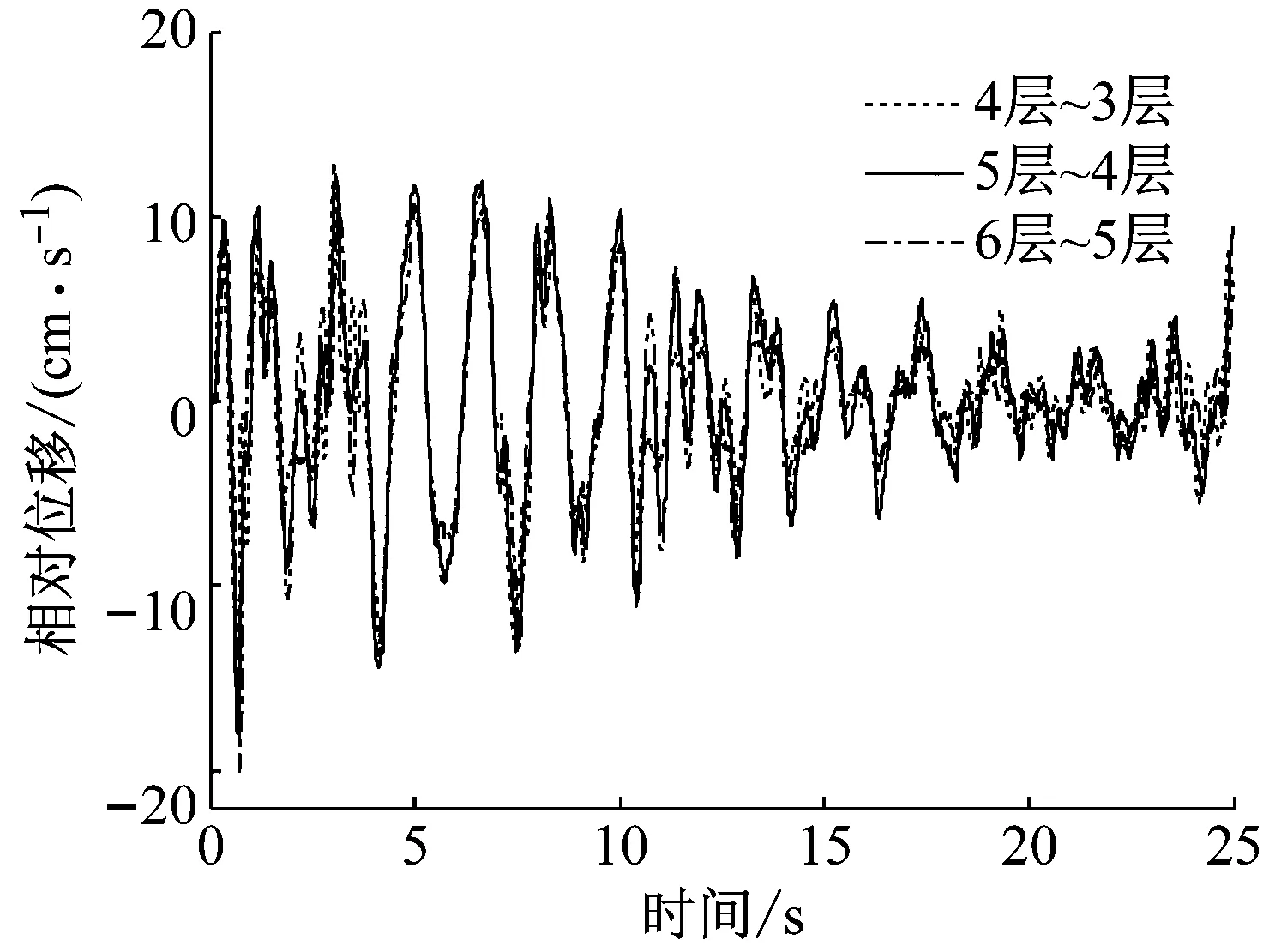
图3 各层间相对速度Fig.3 The relative velocity between different layers

表1 分解层数Tab.1 Layer of parameters
由图4~9可知,无噪音时各层时变刚度和阻尼识别结果精度很高,只在时变参数发生变化的拐点处稍有偏差,主要是在此时存在较多高频成分,而提出的方法忽略掉了参数的高频变化。在5%噪音时,时变刚度识别结果仍然具有较高的精度,第4层时变阻尼识别结果具有一定波动性和偏差,但仍能较好的识别其变化趋势,其他各层阻尼识别效果较好。因此,算法具有一定抗噪性。总的来看,刚度比阻尼识别结果精度更高,主要是由于结构刚度比阻尼大几个数量级,在进行多分辨率展开时,刚度变化时截断的高频分量损失的能量相对阻尼来说较大,因此对阻尼的识别结果影响较大。
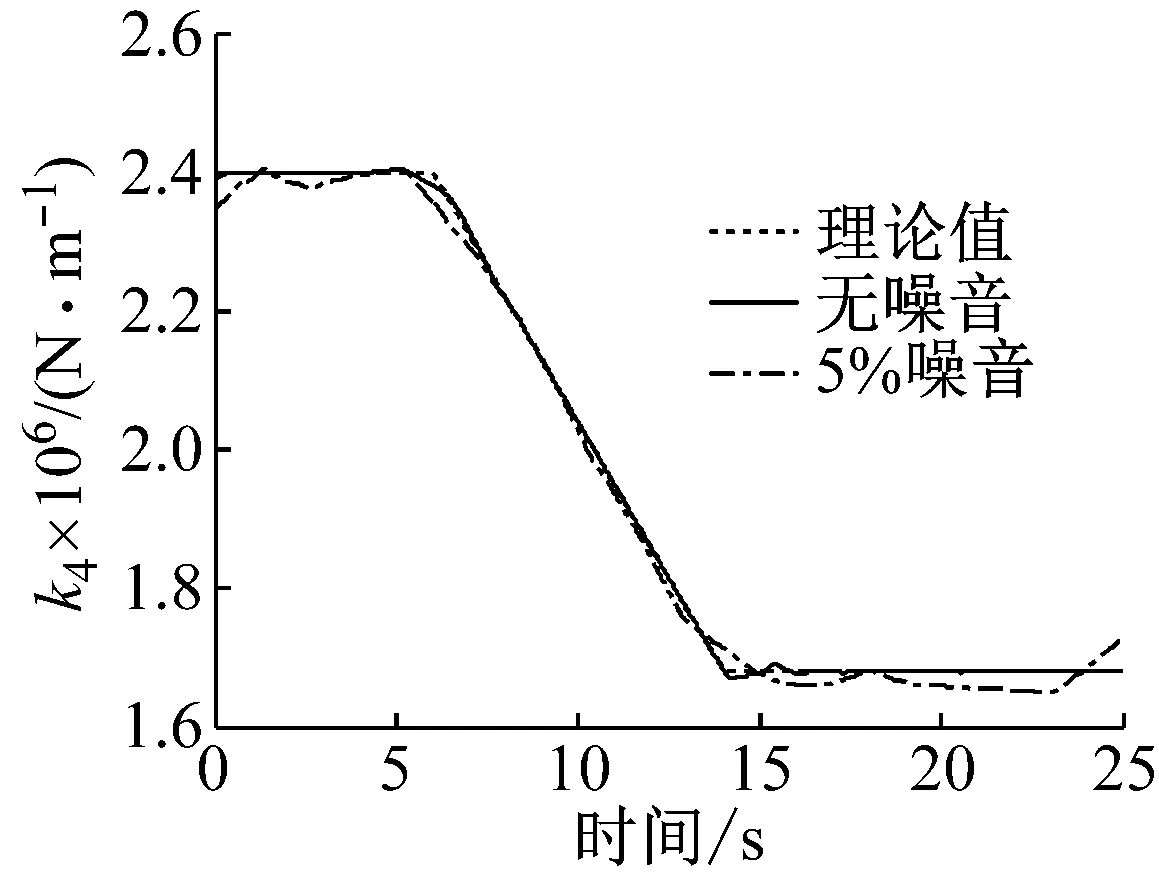
图4 刚度k4识别结果Fig.4 Identification result of k4

图5 阻尼c4识别结果Fig.5 Identification result of c4
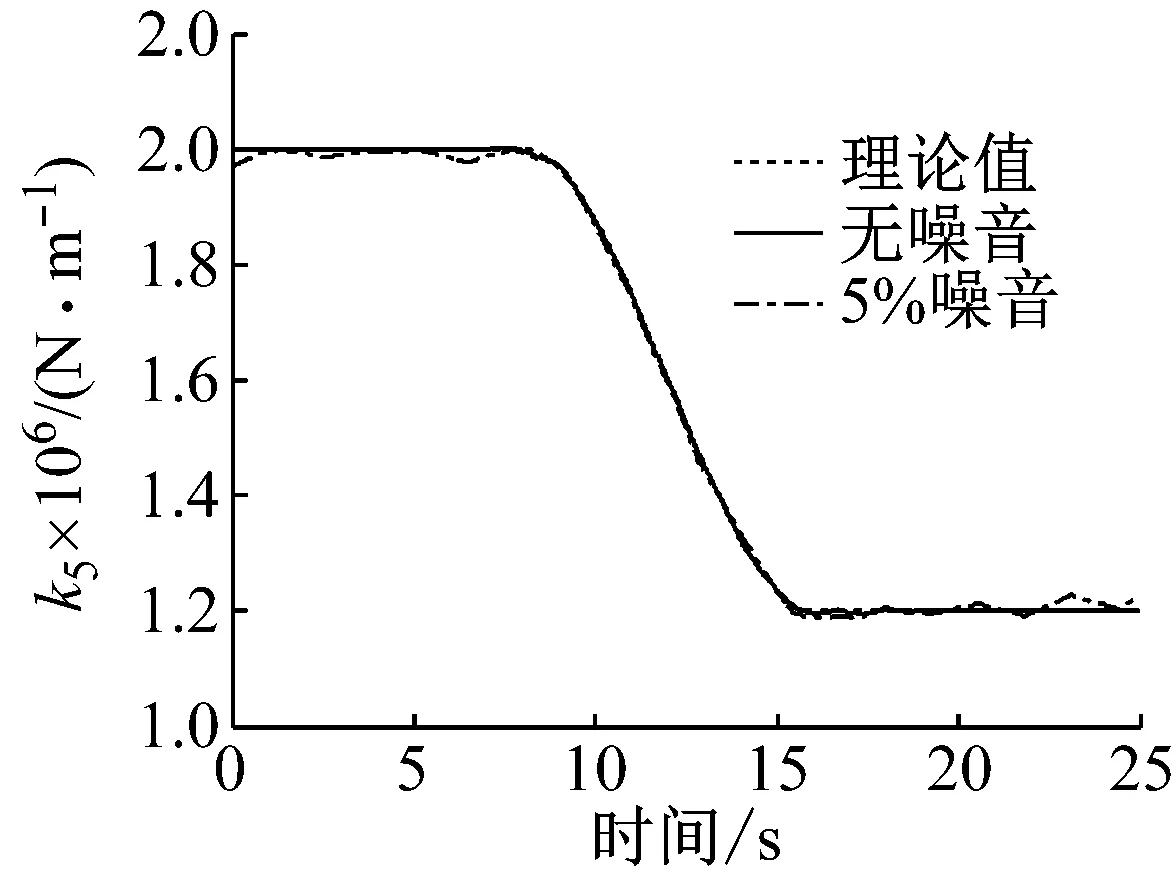
图6 刚度k5识别结果Fig.6 Identification result of k5

图7 阻尼c5识别结果Fig.7 Identification result of c5

图8 刚度k6识别结果Fig.8 Identification result of k6

图9 阻尼c6识别结果Fig.9 Identification result of c6
4 结 论
提出了基于小波变换和子结构法的多层剪切结构时变参数识别方法,数值模型结果表明:
(1) 通过子结构技术,可以只利用结构的部分自由度响应对时变参数进行识别,大大减少了待识别的未知参数,降低了多个时变参数分析层数优化问题的维度,也减小了方程求解的病态问题,而且只需要测量结构部分层的响应,便于实际工程应用。
(2) 无噪音时结构时变刚度和阻尼识别结果精度非常高,添加噪音后,结构刚度比阻尼的识别精度要好,主要是由于刚度比阻尼大几个数量级,在进行多分辨率展开时,刚度变化时截断的高频分量损失的能量相对阻尼来说较大,因此对阻尼的识别结果影响较大。但是阻尼仍然可以较好的识别其变化趋势,方法具有一定的抗噪性。
(3) 识别结果表明对于连续曲线变化的时变参数用db3小波可以得到较好的分析效果,而对于突变变化的参数可以采用haar小波进行分析。
