三角形的（面积）变化

刘善娜（特级教师）

【教学时机】

人教版五年级上册，三角形的面积学习之后。

【教学目标】

1.通过画三角形的草图及“等积变形”，使学生感受三角形面积与平行四边形面积的联系，进一步掌握灵活计算三角形面积的策略。

2.通过从长方形中“切分”三角形，培养学生的几何直观能力。

【教学过程】

一、回顾三角形的“底”“高”特征

1.看式子想图形。

师：看着 5×4÷2=10cm2，请你描述一下这是一个怎样的三角形？请画一个草图，标注相关数据。动作快的话，可以多画几个。

2.欣赏草图，感受“等积”三角形。

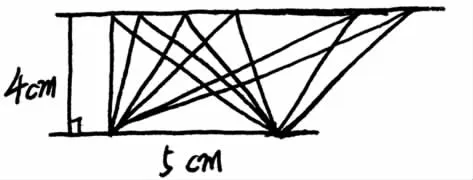
问1：为什么这些三角形的面积都是5×4÷2=10cm2？

问2：同底等高，高的找法，谁再来分享一下？

（强调“从顶点到对应的底边的垂直线段”）

【设计意图：通过了解“同底等高”的三角形的草图，为学生以后学习用“等积变形”解决三角形面积的问题打下基础。】

二、感受三角形与平行四边形的关系

1.画出符合条件的三角形与平行四边形的草图，要求标注数据，再说说你的发现。

（1）三角形与平行四边形，等底等高。

（2）三角形与平行四边形，等底等面积。

（3）三角形与平行四边形，等高等面积。

【设计意图：小学生通过具体的数据比较容易理解“相等”，因此借助给草图标注数据，帮助学生理解较为抽象的“变化”，使学生学会通过画简单的草图来理解问题。】

2.反馈交流。

（1）先交流有错的草图。

方法小结：画草图时可以假设数据，数据与图要有一定的对应；画完之后要“回头看一看”画的图是否符合要求。

（2）观察画得较好的三组草图，试着填一填“等（ ）等（ ），三角形的（ ）是平行四边形的（ ）”。

小结：等底等高，三角形面积是平行四边形面积的一半；等底等面积，三角形的高是平行四边形的高的两倍；等高等面积，三角形的底是平行四边形的底的两倍。

师：为什么后两种情况“等面积”时，作为“弱者”的三角形的“高”和“底”，反而是平行四边形的“高”和“底”的两倍了呢？

【设计意图：在学生的印象中，三角形是“弱者”，他们习惯于回答“三角形的（ ）是平行四边形的一半”。教师结合前面的草图，板画重合式的草图，加深学生的理解。】

3.变式跟进。

画出符合条件的三角形与平行四边形的草图，要求标注数据，再说说你的发现。

（1）三角形与平行四边形面积相等，三角形的底是平行四边形的底的一半，请画出三角形的高与平行四边形的高的关系。

（2）三角形与平行四边形面积相等，三角形的底是平行四边形的底的四倍，请画出三角形的高与平行四边形的高的关系。

师：你是怎么画的？说说步骤。你发现了什么？

（学生交流）

【设计意图：三角形和平行四边形之间的面积变化问题，难度一般不会达到这个程度，但画图的思路、思考问题的方式却和前面是一致的，因此可以通过拓展使学生进一步掌握画图分析的技能。】

三、体验长方形中分割三角形的多种情况

1.画出具体的裁切草图。

在一张长12cm、宽8cm的长方形纸上剪两条直角边分别为2cm和3cm的直角三角形，最多能剪几个？

2.理解题意，厘清思路。

画长方形，标注数据（师生都画好长方形、标好数据）→画三角形→算个数。

3.展示交流。

（请学生说画法，教师板画）

问1：为什么先分割成小长方形？

问2：式子中的两个“8”分别表示什么意思？

问3：如果还是这张纸，现在剪的直角三角形的一条直角边不变还是3厘米，另一条直角边变长一些，从2厘米变成3厘米，请你估估看，现在大约能剪多少个这样的三角形？

A.30～39个 B.20～29个 C.10～19个

4.画图验证。

师：为什么只有16个，和预估差这么远？

师：大图形中裁切小图形，有可能不浪费，是正好的，也有可能会浪费，数个数的好方法是什么？

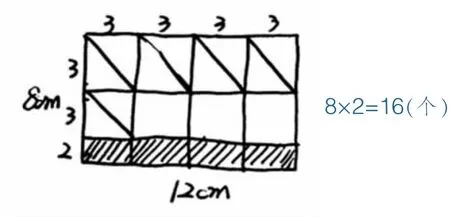
小结：利用草图，确定一行最多能裁切几个，一列最多能裁切几个。

【设计意图：学生喜欢通过“长方形面积÷三角形面积”来求三角形的个数，这种算法只适用于“没有多余”的情况。通过画图、估算，学生会明白只有从“行”和“列”的角度去思考个数，才是合理的。】

四、全课总结

师：学了关于三角形面积问题的各种相关草图，你有什么收获？

【教学建议】

本课内容是在学生学完三角形面积后进行教学的。一旦本课的教学目标达成，练习课的课时就可以适当缩短。在实际教学中要把握好以下两点：

一、把握好“种子课”特质，充分积累经验

“种子课”特质分两层含义，通俗地说，其一为“本身就很重要”，尽可能让每位学生都掌握。在教学中，要有充分的时间，让学生动手画，可以尝试画、可以跟着画、可以巩固画。其二为“对后续学习很重要”，等底等高的圆柱和圆锥的关系就与本课研究的关系类似，教师需要有为后续发散做好经验储备的意识，让学生在较为简单的平面图形学习阶段里体验到各种变化，巩固相关经验。

二、既要强调“假设数据”作图，也要关注“回头看一看”的正向验证

学生下意识就会认为平行四边形比三角形要大，因为三角形的面积计算公式推导的过程和结果都在给予他们这样的印象。如果告知等底等高，学生对两者面积的判断就是一种正向的验证。但如果告知底和面积相等，让学生对高作出判断，就需要逆向思维，相对会有难度。除了让学生多假设数据作图，也要引导学生养成“回头看一看”的习惯。如画一对“等底等面积”的三角形和平行四边形，学生很可能在画出“等底”后又画了“等高”。画的时候，学生会因混乱而画错，但一旦图形真的画出来后，他们也会发现这是“等底等高”，那“面积”一定是平行四边形的大。画图的优点就在于，一旦学生“逆向”失败，画错之后只要肯“回头”用正向思维去看看自己画的图，就能很快纠正错误。