不完全数据下混合两点分布参数的估计与检验

李 阳，赵志文

在统计学研究中，部分缺失数据一直是统计学家值得研究的问题.文献［1］研究了两点分布的相关知识，得到了如何估计产品的合格率，种子的发芽率和两种产品的某种指标是否相等的问题.文献［2］通过对产品寿命的研究，得到了具有部分缺失数据的两个指数的总体参数估计以及假设检验问题.文献［3］通过对混合指数分布总体的研究，得到了不同场合下的混合指数分布总体的参数估计.文献［4］在定数截尾下，利用样本获得估计量，并计算其收敛速度.

1 矩估计及其渐近性

假设混合两点分布的密度函数为f(x,q,γ1,γ2)=

其中，取γi＞0(i=1,2)为第一个总体的未知参数，分别对两个混合两点分布进行n次独立观测，观测时，每一个样本以1-p的概率缺失.第一个总体观测值为(Xi,δi)，i=1,2,…,n，其中，Xi表示第一个混合两点分布总体的第i个样本观测值，若第i个样本值丢失时，记δi=0，否则记δi=1.

下面考虑用矩估计的方法对未知参数p1,p2进行估计.建立矩估计方程为

解此方程得

同理，θi＞0(i=1,2)为第二个总体的未知参数，第二个总体观测值为(Zi,ηi)，其中，Yi表示第二个混合两点分布总体的第i个样本观测值，若第i个样本值丢失时，记ηi=0，否则记ηi=1.得到另一组观测值(Zi,ηi) 后，得到η1,η2的矩估计

对于如上参数γi(i=1,2) ，θi(i=1,2)的矩估计，有下面的相合性和渐近正态性.

证明 {Xiδi，1≤i≤n} 为独立同分布随机变量序列，由强大数定律知a.s.，其中，同理可得

定理2 在上述记号下，有

同理，令

2 两总体参数相等的检验及其两总体参数之差的渐近置信区间

在实际中获得两组样本，那么这两组样本是否来自于一个总体一直是我们关心的问题.因此，可以把一问题理解为检验两个总体参数是否相 等.研 究 的 假 设 检 验 为H0:γ1-θ1=0↔H1:γ1-θ1≠0 ，G0:γ2-θ2=0↔G1:γ2-θ2≠0.

表1 模拟结果

定理3（检验统计量）若为参数γ1的矩 估计，为参数θ1的矩估计，则

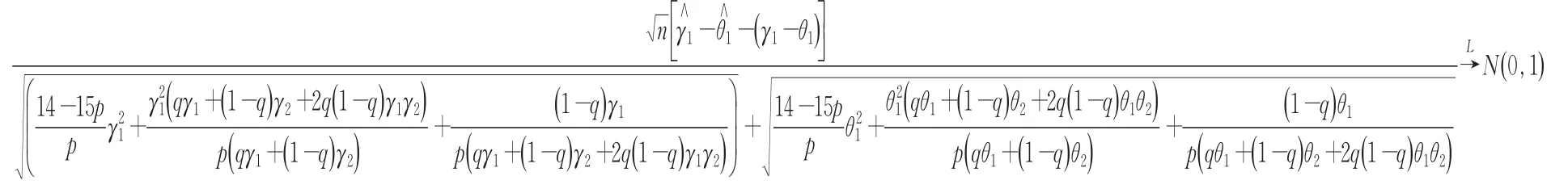
下面研究 Δ 的渐近置信区间，令 Δ1=γ1-θ1.对 于 0＜α＜1，令ξα满足于是得α给定的置信区间，渐近置信区间Δ1为

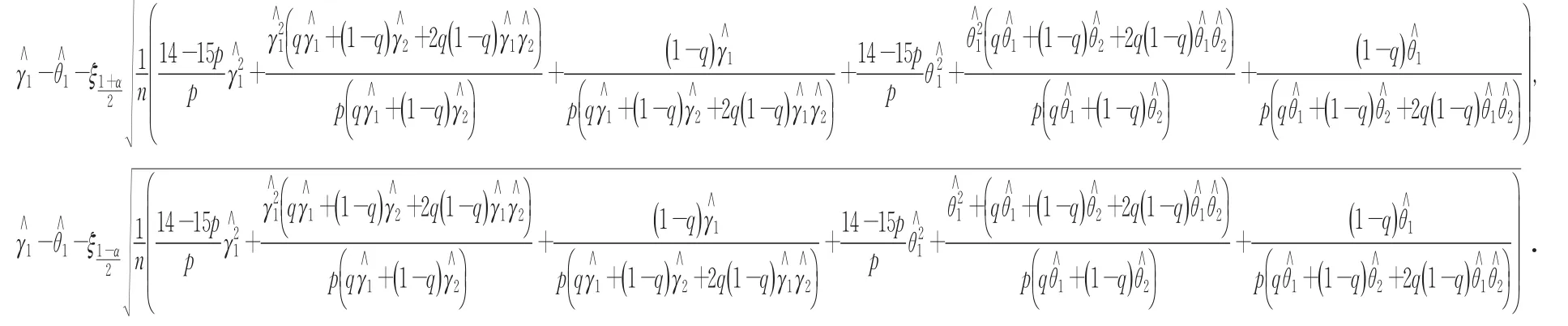
同理，得Δ2=γ2-θ2的渐近置信区间.

3 随机模拟

置信水平取为α=0.95.n=100为样本量，缺失概率为1-P=0.10时的模拟结果如表1所示.其中，参数差的绝对值为分别表示参数γ1，γ2以及参数θ1，θ2的估计的偏差，覆盖率(C.P) 为 | Δ|置信区间以及的平均值为随机模拟500次的结果，覆盖率则为随机模拟500次的覆盖率.

4 结论

本文首先给出混合两点分布的密度函数，并利用矩估计的方法证明估计的相合性以及渐近正态性；其次，讨论混合两点分布参数相等的假设检验，给出检验统计量及其分布，进而得到了两个总体参数之差的置信区间；最后对模型进行随机模拟，结果表明文中方法具有可行性.通过对该方法的研究，为今后研究数据缺失问题打下了基础.