小区开放对出行效率的影响研究

李 勇，林 杰

小区开放，指交通开放小区，是在保证小区内部居住、休闲等正常运行的情况下，把封闭型小区内部的一条或者多条道路与小区外的市政道路连接，供车辆或者行人使用.2016年2月21日，国务院发布《关于进一步加强城市规划建设管理工作的若干意见》，其中第十六条关于推广街区制，原则上不再建设封闭住宅小区，已建成的住宅小区和单位大院要逐步开放等意见［1］.对此，本文通过建立模型对小区开放前后道路的最大通行能力、通行时间以及通过安全性进行计算分析，定量研究小区开放对周边道路通行的影响.

1 建模准备

（1）指标确定.小区开放对周边道路通行的影响主要表现在可通行的最大通行量、通行时间以及安全性三方面［2］.最大通行车流量由车道最大通行能力和车道数决定，通过时间由平均行驶时间和平均延误时间构成，安全性和道路级别有关.对此，建立指标体系［3］，如图1所示.

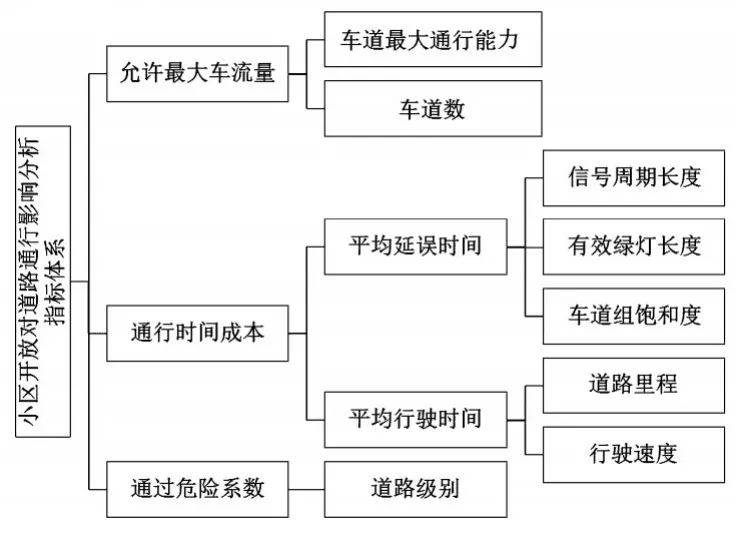
图1 研究问题的分析指标体系

（2）指标解释.车流量：以单位时间内通过某路段的车辆为标准，在一定的时间内，某条公路点上所通过的车辆数.其计算公式为：车流量=车道数×最大通行能力.通过查询资料［4］得到各等级道路上对应不同速度的最大通行能力如表1所示.

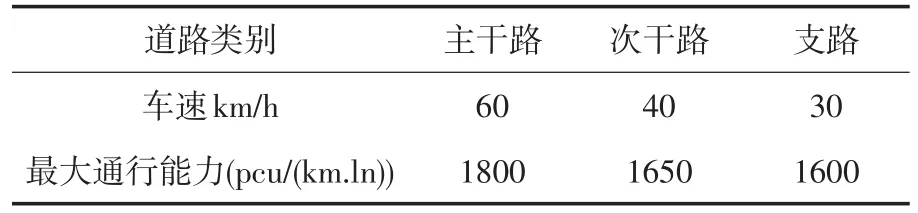
表1 小型汽车在各等级道路上最大通行能力

其中，时间成本为平均行驶时间与平均延误时间之和；平均行驶时间为该路段的实际里程与道路设计平均行驶速度的比值；平均延误时间计算公式［3］为其中，T-信号周期长度；tg-有效绿灯长度；x-车道组饱和度，指在理想条件下，最大服务交通量与基本通行量之比.

危险系数：节点n的危险指数为与节点n邻接的所有路段中任意两路段等级之差的绝对值之和，求解公式为，其中，s为交叉口n的危险系数，xi、xj为任意与节点n相连的路段的道路等级（支路等级为1，次干路等级为2，主干路等级为3）.路段的危险系数为路段总节点危险系数的平均值.道路级别：根据道路的平均行驶速度不同，将道路分为五个级别［4］，如表2所示.

表2 路段平均行驶速度等级划分（单位：km/h）

2 模型建立

2.1 最大流线性规划模型

（1）模型定义.①构建流网络［5］N=(V,A,L,U,D).V：顶点集；A：弧集；L：弧(i,j)∈A对应的权L(i,j)记为lij，称为弧(i,j)的容量下界，此模型中容量下界即最小交通量为零；U：弧(i,j)∈A对应的权U(i,j)记为uij，称为弧(i,j)的容量上界；D：弧(i,j)∈A对应的权D(i,j)记为dij，称为弧(i,j)的供需量.在流网络中找到流值最大的可行流

其中，x表示源点，y表示收点.

（2）算法实现.从容量网络中任意一个可行整数流fij开始，寻找增广链，通过引入剩余网络使可行流沿着最短的增广链进行增广.因为找容量网络中最短增广链等价于求剩余网络中最短(vi,vj)路，此时把寻找增广链过程转化为剩余网络中的最短路过程，然后对其增广［6］.

2.2 最小时间成本模型

（1）模型定义.设v0是一个非负数，最小时间成本就在始点vs和终点vt的容量时间成本网络中求一个定流值为v0，且时间成本最小的可行流，这样的流称为最小费用流.数学模型为

（2）算法实现.对于从顶点i到j不外乎存在经过i与j之间的地点k和不经过地点k两种可能，所以可以令k=1,2,3,…,n，再把从i到j的最小时间成本t(i,j)与从i到k、从k到j的最小时间成本之和t(i,k)+t(k,j)作比较，若有t(i,j)＞t(i,k)+t(k,j)，就表示从i出发经过k再到j的时间成本要比原来的i到j的时间成本少，自然把i到j的t(i,j)重写为t(i,k)+t(k,j)，每当一个k查完了，t(i,j)就是目前的i到j的最小时间成本.重复这一过程，最后当查完所有的k时，t(i,j)里面存放的就是i到j之间的最小时间成本.

2.3 最小危险系数模型

其定义和算法实现与最小时间成本相同，基本思想预算法也与最小时间成本模型相同，令k=1,2,3,…,n，再把从i到j的最小危险系数s(i,j)与从i到k、从k到j的最小危险系数之和s(i,k)+s(k,j)作比较，最后当查完所有的k时，s(i,j)里面存放的就是i到j之间的最小危险系数.

3 实证分析

结合不同类型的小区，研究小区开放后对道路通行产生的影响.文中选取了我国开放较早，小区内部结构和外部道路结构都不相同的上海某小区和四川某小区.通过高德地图获取其小区内部以及周边道路的相关数据，代入上文建立的模型中进行求解分析.

3.1 模型求解

（1）通过高德地图获得上海某小区道路卫星图，该内部开放了两条道路，一条次干路和一条支路，周围三面有两条次干路和一条主干路.

①为了研究问题方便，将此小区开放前后的道路图简化如图2所示.

图2 小区开放前后的简化道路图

②查阅《中国交通年鉴》和高德地图数据，获得道路里程以及设计平均速度等建设数据.根据小区道路级别和城市道路一条车道的通行能力［7］计算求得每条路段最大通行能力，利用最大流线性规划模型，根据每条道路的最大通行能力，分别求出从B1到B3和从C1到C6开放前后每个路段的通过车流量，如表3所示.

表3 开放前后每个路段的通过车流量

③根据求解的最大流方案，根据高德地图中提供的道路交通数据，利用问题二中模型求解出部分路段上的时间成本，如表4所示.

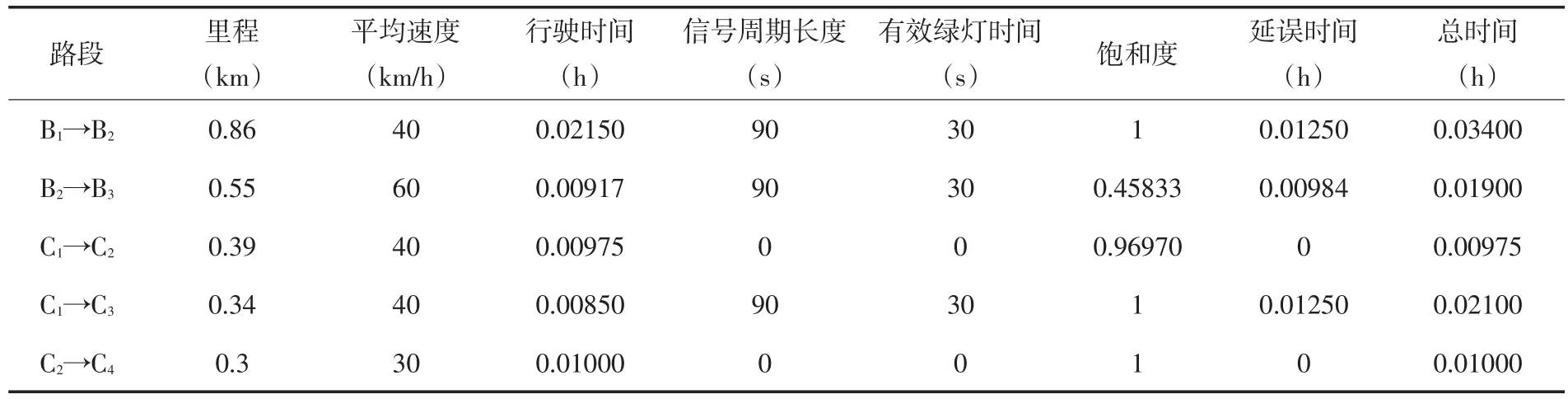
表4 每条路段上的时间成本

④根据危险系数的定义求得通过每个路段的危险系数如表5所示.

表5 每个路段的危险系数

⑤在从B1到B3和从C1到C6过程中，利用模型进行最大流求解后，得到每个路段通过的车流量，根据求解出的每段车流量、时间成本和危险系数，求得小区开放前后从一点到另一点的允许最大车流量、最大车流量下每辆车的平均时间成本和平均危险系数，得到结果如表6所示.

从表6可以看出，小区开放前后，从相同一点到达相同另一点，小区开放后每辆车所需的平均时间成本降低，但是危险系数增加.

表6 小区开放前后从一点到达另一点的最优情况

（2）通过高德地图获得四川某小区道路卫星图，该小区四周有两条主干道和两条次干道，小区内有多条道路已经开放.将该小区开放前后道路图简化的情况如图3所示.

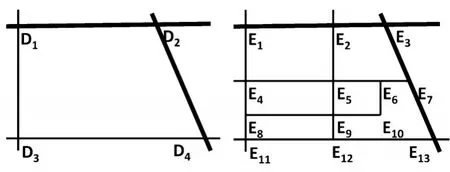
图3 小区开放前后道路图简化图

与上海某小区的求解方法相同，最终求得小区开放前后从一点到达另一点的允许最大车流量、最大车流量下每辆车的平均时间成本和每辆车的平均危险系数如表7所示.

表7 小区开放前后从一点到达另一点的最优情况

此时同样可以得到，小区内部道路开放，可以两点间最大车辆通行能力增加，每辆车平均时间成本降低，但平均危险系数增加.

3.2 模型改进

在求解过程中可以看到，在实现通过能力最大流时，部分开放车道存在通行量为0的情况，此时说明小区内开放此条道路对道路交通没有缓解能力，而且由于交通交叉口的增加，其连接道路的危险系数增大.因此，此时可以考虑封闭对交通压力缓解没有贡献的道路.

对上海某小区，实现通行能力最大流时，C3→C4路段通过量为零，删除此路段，此时求解如表8所示.

针对四川某小区，实现通行能力最大流时，E2→E5、E8→E9、E6→E10、E9→E10路段通过量为零，关闭这些路段，此时求解平均危险系数如表9所示.

通过对两个小区的道路优化可以看出，并不是开放小区内所有道路都对小区和小区周围道路有积极意义.开放部分小区道路，可以缩减出行时间和减小小区周边道路压力，但部分道路的开放对交通压力没有缓解意义，反而因为道路口的增加，给小区居民和驾驶者增加了危险系数.

4 结论

本文创新性地将车辆通行道路网视为流网络，把图论中的最大流最小成本问题应用到道路规划设计中来，通过各指标的量化，代入模型求解，得出了两点间道路的理论最大通行量，通行时间以及危险系数.通过数据将小区开放前后的结果进行对比分析，得出适当开放小区道路能够在保证安全的前提下，缓解道路拥堵，提升出行效率.