3-预李代数的表示与扩张

周 月

近几年，许多学者对3-李双代数及3-李代数上的与经典Yang-Baxter方程类似的结构作了研究，比如在文献［1］中研究了3-李代数和3-李余代数以及3-李双代数之间的关系，在文献［2］中研究了Hom-3-李代数的表示和导子代数扩张，在文献［3］中通过上同调理论得到3-李代数的变形以及3-李代数的交换扩张，在文献［4］中根据李超代数的表示构造一系列的3-李超代数，在文献［5］中研究了3-李代数的经典杨-巴斯特方程，在文献［6］中研究了3-李代数的交换扩张和广义表示.本文考虑3-李代数的表示、配对以及扩张在3-预李代数上的推广，为研究3-预李双代数提供了基础.

1 3-预李代数的配对

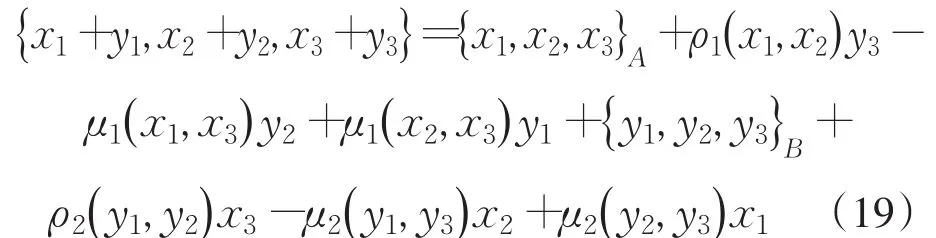
2 3-预李代数的广义表示

定义2 设(A ,{⋅ , ⋅,⋅}) 是3-预李代数，V是线性空间和为线性映射，如果任意 xi∈A,vi∈V(1 ≤i≤5 )满足

则称(V,ρ,μ,r1,r2)为3-预李代数 (A,{⋅ , ⋅,⋅})的广义表示.

定理2设(A,{⋅ , ⋅,⋅}A)是3-预李代数，V是线性空间 ，ρ、μ：⊗2A→gl(V) 和r1、r2：A→Hom(⊗2V,V) 为线性映射，在A⊕V上定义

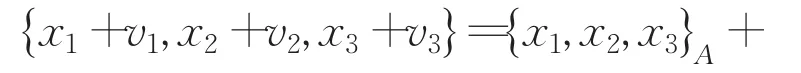
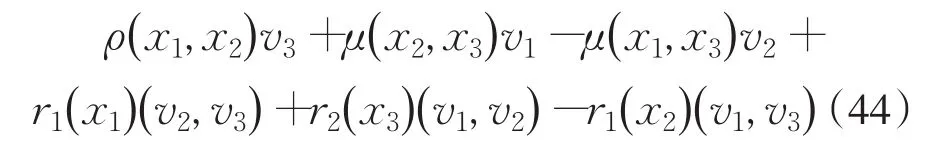
其中，xi∈A,vi∈V(1 ≤i≤3)，则 (A⊕V,{⋅ , ⋅,⋅})是3-预李代数的充要条件是(V,ρ,μ,r1,r2)为3-预李代数(A,{⋅ , ⋅,⋅}A)的广义表示.

3 3-预李代数的非交换扩张

定理3 (A⊕B,{⋅ , ⋅,⋅})是3-预李代数的充要条件是对于任意xi∈A,vi∈B(1 ≤i≤5 )满足