线面积分重要公式的问题式教学探讨

吴世玕

曲线积分、曲面积分中格林公式、斯托克斯公式、高斯公式［1］是重要的公式，用这些公式，可以实现平面上闭曲线积分与二重积分的转化，空间闭曲线积分与曲面积分的转化，闭曲面积分与三重积分的转化，对化简积分及积分的理论研究都有非常重要的意义［2-3］.如何进行这部分内容的教学，也非常值得研究.笔者对这部分内容的教学，进行问题式教学探索，希望与其他数学老师分享教学方法，也希望本文对大学生学习高等数学、数学分析有所帮助.

1 格林公式的引入

假设闭区域D由分段光滑的曲线L围成，在D上连续，穿过区域D内部且平行于坐标轴的直线与D的边界曲线L的交点恰好为两点，即区域D既是X型又是Y型的情形.如果L取逆时针方向，则可得到结论

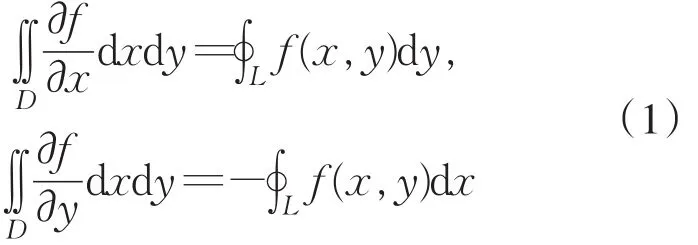
如果区域D不满足以上要求，也可作辅助线，将区域D分成有限个小区域，每个小区域都满足上述要求，且辅助线上的曲线积分互相抵消，从而（1）式仍然成立.

问题2 一般的平面闭曲线积分与二重积分有何联系？

其中，P(x,y),Q(x,y)在D上具有一阶连续偏导数，L是D的正向边界闭曲线.称公式（2）为格林公式.

一般的高等数学及数学分析教材，都是直接给出形如（2）的格林公式，然后再证明.这样就缺少一个由浅入深的探索过程，缺少模仿创新的训练，缺少数学抽象思维的训练过程.可以模仿牛顿—莱布尼兹公式的结构，将其思想方法引入到平面曲线积分与二重积分上.先得到公式（1），再得到公式（2），其引入过程是逐步深入的.模仿往往是数学上获得新知识的手段.

2 斯托克斯公式的引入

格林公式反映了平面曲线积分与二重积分的联系，由公式（1）知

问题3 曲线积分∮ΓP(x,y,z)dx与P(x,y,z)的偏导数在以Γ为边界的曲面上的曲面积分有何联系？

设∑是以Γ为边界的分片光滑有向曲面，Γ的正向与∑的侧符合右手规则，P(x,y,z)在曲面∑（连同边界Γ）上具有一阶连续偏导数.设∑与平行于z轴的直线相交不多于一点，并设∑为曲面z=f(x,y)的上侧，有向曲线Γ在xoy面上的投影为平面有向曲线C，C所围成的闭区域为Dxy，曲线C是Dxy的正向边界曲线.f(x,y)在区域Dxy上有连续的一阶偏导数.由格林公式（3）得记曲面∑的法向量为则由复合函数求导法则及对坐标的曲面积分知由此可得

设有向曲线C参数方程为x=φ(t),y=ψ(t),t从t1到t2，则有向曲线 Γ的参数方程为x=φ(t),y=ψ(t),z=f(φ(t),ψ(t)),t从t1到t2.从而有，于是得到为了便于推广和记忆，可以将此式写成

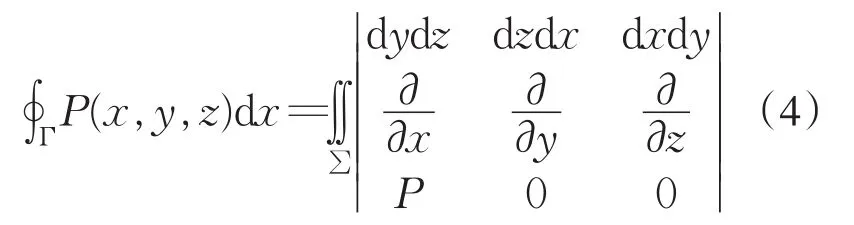
将（4）式推广到更一般的形式为

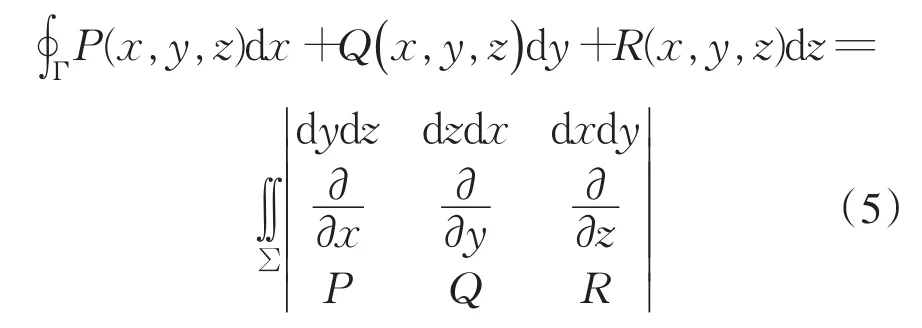
公式（5）为斯托克斯公式.

由一个函数形式的格林公式（3），将平面情形向曲面情形转变，将平面曲线向空间曲线转变，演绎出了一个函数情形的斯托克斯公式（4）.这可见斯托克斯公式是格林公式向空间曲线积分的推广.先引出一个函数积分的情形，再向三个函数积分合写形式推广，得到三个积分合写的斯托克斯公式.认识问题由浅入深，由简到繁，符合学生的认识规律.通过逐渐引入，让学生有一个探索、思维、模仿创新的过程，训练了学生的数学思维方法.

问题5 格林公式与斯托克斯公式有何联系？

由格林公式（3）出发，引出了斯托克斯公式（4），进一步推广到公式（5），这说明斯托克斯公式是格林公式由平面向空间的推广.

若取∑是xoy面上区域D，取向上一侧，C为D的正向边界曲线，由公式（5）得

公式（6）就是格林公式（3）.这说明格林公式是斯托克斯公式在平面上的特例.

3 高斯公式的引入

问题6 闭曲面积分与三重积分有何联系？

格林公式、斯托克斯公式表明，多元函数的偏导数在区域内、曲面块上的积分与原函数在区域或曲面边界上的曲线积分有一定的联系.那么，多元函数偏导数在空间闭区域Ω内的三重积分与函数在边界曲面上的曲面积分是否有一定的联系？从物质守恒定律来说，设∑表示Ω 的表面，则R(x,y,z)dxdy，它表示流向曲面指定侧的流量.那么，这些流量不可能凭空产生或消失.

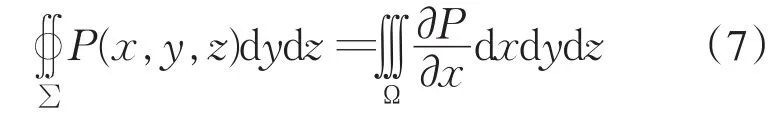
若穿过Ω内部且平行于坐标轴的直线与Ω的边界曲面∑的交点多于两个，可以引进几张辅助曲面把Ω分为有限个闭区域，使得每个闭区域都满足：平行于坐标轴的直线与Ω的边界曲面相交恰好有两个交点.沿辅助面正反两侧面的积分正好抵消.这样公式（7）仍然成立.更一般地，公式（7）可推广到一般的高斯公式

4 结论

平铺直叙，直接给出要教的新知识，学生难以理解这些新知识与旧知识的关系.学生学起来很被动，缺泛主动性.如果从旧知识中提炼出本质性的东西，从深度和广度方面探讨，加以拓展知识，使本质性的东西得到推广，产生新知识.这样，学生更容易接受，学起来就会更主动，积极参与到教学的探讨过程中.教学，必须要有问题，对问题展开讨论，并解决问题，或给出展望，才能吸引学生的积极性，让学生产生学习的兴趣.

格林公式、斯托克斯公式、高斯公式都要求被积函数在积分曲线、积分曲面及其包围的范围内有一阶连续偏导数.如果，被积函数在某些点处没定义，或没有一阶连续偏导数，该如何解决问题？有兴趣的同学可以参考文献［2-3］中的一些例题，总结出解决问题的方法.