公路运输环境下运输车及导弹固体发动机响应数值分析

刘跃龙， 李天鹏， 安振涛

(陆军工程大学石家庄校区弹药工程系， 河北 石家庄 050003)

固体火箭发动机的公路运输安全性不仅关系到战术导弹的作战保障效率，还直接影响着各项战术性能的发挥。为使导弹具备更稳定的内弹道性能，药柱设计通常采用复杂的内通道形状，使得发动机在环境载荷作用下的应力更为集中；另外，为满足远射程要求而进行的大长径比设计，增大了发动机的柔性及运输路况的复杂性，这均加剧了其在运输过程中的动力学响应[1]。同时，承载的环境温度对发动机结构完整性也产生着较大影响[2-3]。因此，开展公路运输环境下固体火箭发动机的安全性评估，主要是研究不同运输工况下随机振动载荷与环境温度载荷联合作用对发动机结构完整性产生的影响及响应规律。

目前，有关上述研究的报道较多，如：刘兵吉[4]通过理论推导，就随机振动载荷对发动机结构可靠性的损伤进行量化，但计算过程相对复杂，涉及参数较多；徐新琦等[5]以加速度功率谱密度为激励，仿真分析了不同运输工况下发动机药柱的随机振动响应分布；CAO等[6]通过试验研究发现，运输过程中的随机振动载荷主要集中在0.2～15 Hz，且最大应力集中在药柱与粘结层界面上。近年来，针对舰船随机振动与温度环境对发动机药柱结构完整性及粘结界面性能影响开展的一系列研究[7-9]显示：温度和舰船振动载荷均在一定程度上缩短了发动机寿命，但都不致于造成发动机的强度破坏。此外，吴邵庆等[1]依据构建的运输车-弹体耦合模型，计算总结了运输工况改变对弹体动力学响应的影响规律，但未考虑温度与振动载荷联合作用对发动机装药各部件造成的影响，计算结果偏于保守。张巍耀等[10]则利用频域法和3-σ法定量计算了由随机振动载荷导致的累积损伤，并预估了战斗部装药的运输失效时间，对进一步分析固体火箭发动机运输寿命具有一定参考意义。

上述研究成果对发动机结构设计改进、服役寿命预测以及运输防护措施提出均具有参考价值，但也存在着运输车辆建模过于简化、难以反映实际振动响应规律[11-12]，以及频域法不能体现响应随时间变化趋势等缺陷[13]。基于此，笔者构建某型战术导弹运输车的简化模型，基于谐波叠加法模拟标准规定的等级公路路面不平度，并对车身质心处动力学时域响应及规律进行数值分析；同时采用MSC.Nastran仿真分析不同运输工况下发动机的响应分布规律，并与同时施加温度载荷的发动机响应分布作对比，为固体火箭发动机的公路运输安全性评估提供参考依据。

1 车辆动力学模型构建

由路面不平度所造成的振动载荷具有平稳随机性、各态历经性等特性，仅通过正弦交变载荷模拟或采用其他车辆参数不能完全表征发动机承载的振动载荷，必须进行专用运输车载荷谱分析[14]。但直接测定运输载荷谱耗费巨大，且存在安全风险。因此，有必要构建能反映车辆振动性能的简化动力学模型，且整车模型计算精度一般优于1/2车或其他简化模型[15]。

1.1 整车模型构建及参数定义

结合实测参数，构建了某型战术导弹专用运输车13自由度整车动力学模型，如图1所示，其相关简化假设如下：1) 车身、车架及各车轴均假定为刚性体，且垂直于铅垂面；2) 模型左右对称，悬架质量与轮胎的刚度、阻尼均为定常数，且左右完全相等；3) 车辆做匀速直线运动，不考虑转弯、刹车等复杂情况，且整车模型在平衡位置附近做小幅振动；4) 行驶过程中，轮胎始终与地面保持点接触，无跳起；5) 运载弹药质量较大，忽略箱体间的缓冲作用，即假定储运箱与弹药和车厢均为刚性连接。

图1中：x0为垂向运动位移，θ为俯仰运动角，φ为侧倾运动角，其为车身的3个自由度；xij(i=l,r；j=1,2,…,5)为车身i侧第j个悬架的垂向运动位移，其中“l”“r”分别代表车身的左、右侧；sij(i=l,r;j=1,2,…,5)为车身i侧第j个悬架所在车轮所承载的路面不平度激励；m0为车身与运载弹药质量之和；mj为第j轴轮上悬挂质量，车身左右完全一致；cj、kj分别为第j轴悬挂等效阻尼和刚度系数；cp、kp(p=j+5)分别为第p轮轮胎等效阻尼和刚度系数；w为车身宽度；l1，l2，…，l5分别为各轴至车身质心处距离。

若忽略行驶过程中各轮承载激励的差异，则会降低响应计算精度，进而可能对发动机的公路运输安全性产生错误评估。因此，笔者认为所采用的整车模型中同轴轮胎间激励存在相位差，不同轴轮胎间激励存在时间差。为不失一般性，激励相位差取π/2[16]，前、后各轮时滞关系为

sij(t)=si(j+1)(t+Dl/v)，

(1)

式中：Dl为轴间距；t为运输车行驶时间；v为运输车行驶速度。

1.2 路面不平度模拟

本文采用谐波叠加法模拟生成路面不平度，该方法通过一定离散数量的正弦波叠加模拟不平度，应用范围广，算法严密[17]。其位移激励的时域模型输入

(2)

式中：N为划分的时间频率区间个数，取N=5 000；fmid_d为第d个区间的中心时间频率；Dfd为时间频率区间长度；βd为介于[0,2π]间的随机数；

(3)

为fmid_d的功率谱密度，其中n0为参考空间频率(一般取0.1 m-1)，Gs(n0)为路面不平度系数(mm2/m)。

采用Pwelch法对生成的3种路面随机不平度进行功率谱密度估计[18]，并与标准规定的路面随机不平度功率谱密度进行比较，取双对数坐标，如图2所示。由图2可以看出：采用谐波叠加法模拟生成的路面随机不平度与标准规定吻合良好，满足工程应用需求。

1.3 动力学方程构建

依据图1构建整车动力学模型，并基于达朗贝尔原理构建该专用运输车的拉格朗日方程组。

车身垂向动力学方程为

(4)

车身俯仰动力学方程为

(5)

车身侧倾动力学方程为

(6)

轮1垂向动力学方程为

(7)

轮2垂向动力学方程为

(8)

轮3垂向动力学方程为

(9)

轮4垂向动力学方程为

(10)

轮5垂向动力学方程为

(11)

式中：J1、J2分别为车身俯仰和侧倾转动惯量。

将式(7)-(11)整理后，采用矩阵形式可表达为

(12)

模型的动力学响应需采用一种改进的4阶龙格库塔法进行求解[19]。将动力学方程组转化为状态空间方程

(13)

2 车身动力学响应及规律分析

结合《固体火箭发动机公路运输试验方法》[20]规定，并综合考虑运输车的行驶速度及运输路况,设置仿真计算的运输工况，如表1所示。

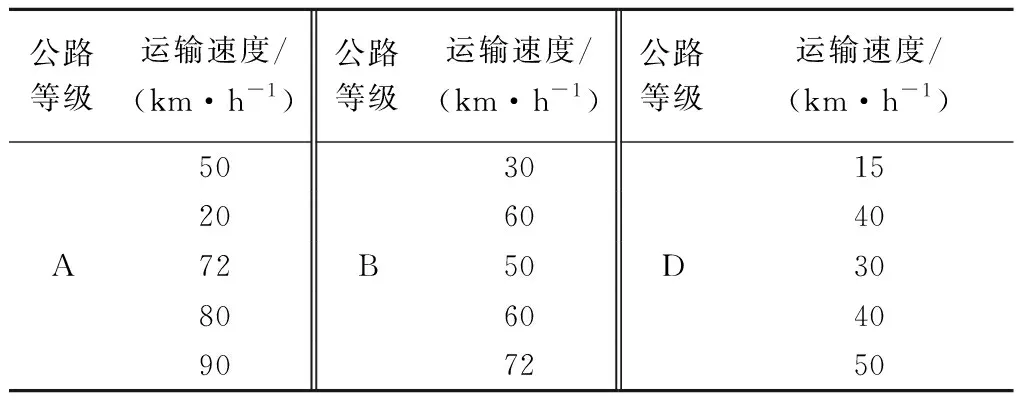
表1 仿真计算的运输车运输工况

仿真计算所需动力学参数参考文献[21]。某次运输过程中，加速度功率谱密度的试验值与仿真计算值对比如图3所示。可以看出：在主频段，仿真计算值与试验值基本一致，说明构建的车辆动力学模型可以满足工程计算需求;但由于受其他次要因素的影响，仿真计算值与试验值仍存在一定误差，表明车辆动力学模型仍需进一步改进。

加速度响应均方根(Root Mean Square，RMS)反映一段时间内作用于结构上随机振动总能量的大小，其值越大，表明单位运输里程内对运载弹药造成的损伤越严重。图4为不同运输工况下车厢质心处RMS随运输速度的变化曲线。可以看出：公路等级相同时，RMS随运输速度的增大先迅速上升后趋于平缓；随公路的等级下降，RMS前期上升趋势更为明显。上述结果表明：公路等级相同时，由于路面随机不平度变化较小，运输速度的提升对车身质心处加速度激励影响作用有限；而随着公路等级的下降，路面随机不平度激励也随之迅速增大，这就造成了RMS前期上升速度的攀升，更进一步说明了公路等级和运输速度的相互促进作用。

车厢质心处加速度响应分布近似服从一种高斯分布，其拟合方程为

y=y0+Aexp(-0.5((x-xc)/μ)2)。

(14)

用拟合方差R2表示加速度响应分布曲线的拟合效果，其值越接近1，表明拟合效果越好。拟合参数如表2所示。

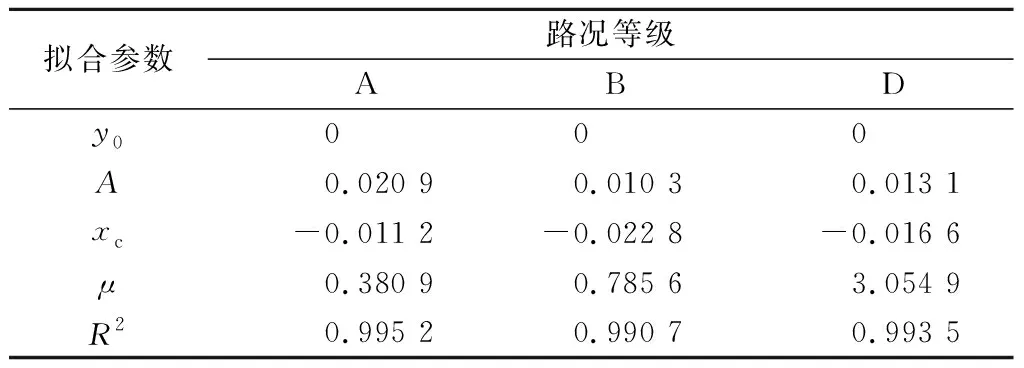
表2 加速度响应分布曲线方程拟合参数

运输车以50 km/h运输速度分别行驶在A、B、D三种等级路面时，其车身质心处加速度响应分布拟合曲线如图5所示。可以看出：D级公路加速度响应的1σ区间，基本完全覆盖了A、B两种等级路面下加速度响应的全区间，更直观说明公路等级变化对随机振动载荷产生的影响。上述结果表明：研究公路运输过程中随机振动载荷对发动机结构完整性的影响很有必要。

3 发动机响应算例分析

研究对象为某战术导弹固体发动机的后半段，其装药为圆柱形通道，其燃烧室主要包括壳体、绝热层、包覆层与药柱。其中：发动机壳体与绝热层视为弹性材料；而包覆层与药柱则处理为同种黏弹性材料。为简化计算，材料泊松比均假定为定常数。同时在有限元分析过程中，采用4参数Burgers模型描述药柱与包覆层黏弹性性能，相关的性能参数如表3所示[3，22]。

表3 发动机各结构材料性能参数

构建发动机有限元模型时忽略长度影响，将动力学响应处理为平面应变问题，并采用Quad4单元进行网格划分，其模型共有 9 300个单元，9 610个节点。运输时，因发动机由弹卡固定，则壳体上半部受固定约束，下半部承载随机加速度载荷a，整体载荷分布特征如图6所示。另外，根据整车动力学模型构建时所作的假设，可认为车身质心处响应即为发动机壳体承载的激励。该型战术导弹在运输作业前，通常贮存在常温库房内，而温度应力、应变与环境温度差成正比[23]。因此，考虑实际运输过程中最严峻的工况，即低温(-40 ℃)条件下，以50 km/h运输速度在D级公路行驶。

工程上常用强度理论评估弹性材料的结构完整性；而对于推进剂药柱这种黏弹性材料，一般则采用von Mises应变作为其破坏判据。其中：发动机壳体屈服强度约为1 500 MPa，推进剂低温时的许用应变约为40%。图7为发动机分别在加速度载荷及其与温度载荷联合作用下的von Mises应力响应分布云图。可以看出：应力集中现象均发生在载荷作用边界；当加速度载荷单独作用时，发动机壳体最大应力为357 MPa，联合作用时则为550 MPa，安全系数则由4.2降至2.7，说明公路等级较低时，2种作用载荷的影响程度相似。

除去发动机壳体、绝热层与包覆层后，药柱的von Mises应变响应分布云图如图8所示。可以看出：药柱的应变集中现象均发生在载荷作用中轴线上，这表明现有导弹储运箱固定方式需要作进一步优化设计；2种载荷作用条件下，药柱的最大应变分别为2.78%和7.56%，均远小于许用应变值40%，也说明温度载荷对药柱结构完整性的影响作用可能要高于加速度载荷。

4 结论

基于相关假设构建的某型战术导弹专用运输车13自由度空间动力学模型，能够较好地反映实际运输工况下车辆主频段振动性能。结果表明：车身质心处加速度时域响应近似服从高斯分布，其均方根值随运输工况恶化总体呈上升趋势，且受路面等级变化影响较大；短时的低温与D级公路运输联合作用下，发动机结构完整性仍能得到有效保证，药柱安全裕度充足。下一步，需要关注固定位置的应力、应变集中现象，同时由远距离或多次运输造成药柱的累积损伤有待于计算验证。