车辆装备单部件系统功能检测间隔期建模

2018-10-19李慧梅封会娟

装甲兵工程学院学报 2018年4期

周刚，李慧梅，封会娟

(1. 陆军军事交通学院学员五大队, 天津 300161； 2. 陆军军事交通学院投送装备保障系，天津 300161)

车辆装备故障可分为突发故障和缓变故障。其中：突发故障是指车辆装备在发生故障前没有征兆，其发生过程具有突然性；缓变故障是指车辆装备在发生故障前会出现征兆示警(潜在故障)，若不及时采取措施消除潜在故障，则发展成为功能性故障，导致系统因故障而停机或发生灾难性的后果，其发生过程具有缓变性。

车辆装备故障大多数为缓变故障，通常采用P-F曲线来描述，且采用视情维修方式进行维修。在车辆装备维修实践中，通常依据监控和检测产品状态信息进行视情维修决策，实现“以检定修”的目的，在预防性维修工作中该类工作称为功能检测，因此，若要确定车辆装备的视情维修时机，只需确定功能检测间隔期。

目前，已有诸多学者对功能检测间隔期进行了研究。如：张向龙等[1]基于武器装备战备完好率要求，以技术准备完好率为决策目标，建立了功能检测间隔期模型，并得到检测间隔期的最优解；葛恩顺等[2]基于检测的不完备性，结合检测出现的虚警和漏检等情况，建立了装备多级劣化系统的马尔科夫模型，并以装备长期使用费用为决策目标，对功能检测间隔期和维修阈值进行了优化研究；XU等[3]针对现代装备结构复杂、运行环境恶劣、维修耗资大等特点，以每个运行周期维修费用为决策目标，基于马尔科夫-蒙特卡罗仿真模型研究了装备状态检测间隔期；张仕新等[4]根据状态检测的不完善性，以装备可用度为决策目标，基于时间延迟理论模型对有限使用期下的装备检测间隔期进行了研究。

然而，针对车辆装备的相关研究仍然相对较少，但在部队车辆维修实践中，随着车辆装备性能逐渐劣化，为避免出现产品故障或系统停机，应及时确定车辆装备的功能检测间隔期。因此，笔者利用连续时间马尔科夫链模型，研究了车辆装备功能检测间隔期的确定方法，为部队维修工作决策提供方法支持。

1 模型假设及参数说明

根据车辆装备维修实际情况进行如下假设：

1) 研究对象为单故障模式的单部件系统(以下称为“产品”)。

2) 产品初始故障率为0，随着产品工作时间t的增加，其性能劣化情况逐渐加深，直至出现功能性故障。产品性能劣化状态可分为k个阶段，其在第k个性能劣化阶段后发生功能性故障，相邻2个劣化状态之间的转移时间1/λ服从参数为λ的指数分布。

3) 产品的性能劣化水平可检测，且检测效果是完备的。

4) 定期对产品状态进行检测，其中平均检测间隔=1/λin，平均检测时间=1/μin，且二者服从指数分布。

5) 若检测到产品处在第i(0≤i≤k)个劣化状态，则产品的维修策略为

(1)

其中n为维修阈值。

6) 在检测时，若发现产品出现潜在故障，则进行预防性维修，且为完全维修，即“修复如新”，并记平均维修时间为1/μR；若产品发生功能性故障，则更换故障件，并记平均更换时间为1/μF。

7) 产品发生故障后的送修、返修时间和费用忽略不计。

模型涉及的相关参数说明如下：

1)T为功能检测间隔期，即T=1/λin；

2)k为产品性能劣化阶段；

3)R(t)为产品可靠度；

4)CR、CF分别为每次预防性维修和更换故障件的平均费用，其中包括停机损失费；

5)Cr为因产品检测而引起的损失费用率；

2 功能检测间隔期模型建立

2.1 模型状态空间定义

根据假设，定义模型状态空间如下：

S(i,0)，1≤i≤k，表示车辆装备的劣化状态；

I(i,1)，1≤i≤n，表示车辆装备在第i个状态正在进行检测；

I(m,1)，n+1≤m≤k，表示车辆装备状态已超过维修阈值，处于检测过程中；

R表示车辆装备处于预防性维修状态；

SF表示车辆装备处于功能性故障状态。

对车辆装备进行定期检测，若未超过维修阈值n则正常工作，超过维修阈值n则进行预防性维修；若发生功能性故障，则立即进行更换。预防性维修和故障件更换均使产品恢复至全新状态。所有状态及转移概率构成的马尔科夫链即状态转移情况，如图1所示。

2.2 模型分析与建立

根据决策目标可将功能检测间隔期模型分为可用度模型、费用(率)模型、故障风险模型和多目标优化模型。在部队车辆装备维修实践中，产品的可用度和费用是进行维修决策需考虑的重要因素，因此，笔者重点以可用度和维修费用率为决策目标进行建模。

2.2.1 可用度决策目标模型

根据可靠性相关理论可知：产品的瞬时可用度为产品在t时刻处于工作状态S(i,0)(1≤i≤k)的概率之和。其求解过程十分复杂，而根据连续时间马尔科夫过程的性质，产品在长时间工作后会进入稳定状态[5]，则产品进入某一状态的速率等于离开该状态的速率，即

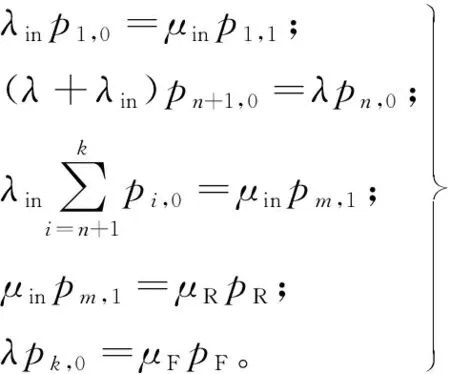
(2)

式中：pi,j为各状态的概率，1≤i≤k，j=0或1;pR为预防性维修的概率;pF为发生功能性故障的概率。

在稳态条件下，产品各状态概率之间的关系：

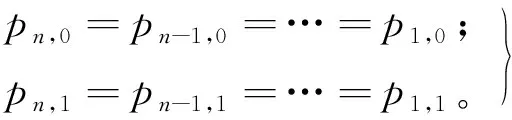
(3)

由于连续时间马尔科夫过程的各状态概率之和等于1，则

(4)

由可用度定义可知：产品稳态可用度为

(5)

则根据式(2)-(5)可得产品稳态可用度

(6)

式中：a=λin/μin；b=λ/μF；c=λin/μF；d=μin/μR；e=λ/(λ+λin)；f=ek-n；g=e(1-f)/(1-e)。

2.2.2 维修费用率决策目标模型

对于长期运行的产品，可采用产品长期维修费用率作为决策目标。产品长期维修费用率是指产品总维修费用与运行总时间的比值，是维修经济性的重要度量指标，其计算公式为

(7)

将式(2)、(3)代入式(7),并经简化可得

(8)

2.3 模型计算

采用数值求解方法计算车辆装备单部件系统功能检测间隔期模型比较繁琐，而且在人工计算过程中，容易因计算及操作失误而导致计算结果误差较大。因此，笔者提出了粒子群(Partical Swarm Optimization,PSO)求解算法，PSO算法流程如图2所示。

具体实施步骤如下：

1) 初始化粒子群，主要包括种群的群体规模N，单个粒子的初始位置xi和初始速度vi。

2) 计算种群单个粒子的适应度，使种群内的每个粒子均有一个确定的适应度。

3) 根据适应度分别比较每个粒子的个体极值和全局极值，使种群个体粒子在变量空间内不断寻优，而所有粒子可自动追踪最优粒子，并不断调整其搜索策略。

4)单个粒子迭代并不断更新速度和位置。

5)判断算法是否满足终止条件，若满足则输出最优解；否则返回步骤2)。

3 实例应用

在部队日常训练中，维修费用是车辆装备维修工作考虑的主要因素。因此，从部队车辆装备维修工作的实际情况出发，在实例验证中选用维修费用率模型进行优化计算。

3.1 信息来源

以某型载重车的离合器分离轴承为例，验证模型、算法的合理性和可行性。该型载重车的信息采集方式主要有如下3个方面：1)从厂家获取的信息，主要有该型载重车零部件的关键寿命、产品费用等信息；2)根据通用车辆装备维修分配表(包括该型载重车的维修任务分配表)以及车辆装备维修保障领域专家经验获得的信息；3)通过部队调研获取该型载重车的维修保障信息，包括备件实际维修费用及维修时间等。

该型载重车在工作过程中，其离合器分离轴承的健康情况不断发生劣化，其性能劣化状态可分为9个阶段，即k=9；从当前状态向下一个状态转移的时间1/λ=10 d，平均检测时间1/μin=0.042 d，平均检测费用率Cr=12元/d；进行预防性维修的平均维修时间1/μR=0.167 d，平均维修费用CR=78.7元；进行故障件更换时的平均故障件更换时间1/μF=0.25 d，平均更换费用CF=153.8元。