基于2DPCA的弹道导弹目标特征级综合识别方法

李陆军， 杨 源， 赵兴刚， 潘小平， 王志刚

(1. 93975部队， 新疆 乌鲁木齐 830000； 2. 空军预警学院研究生大队, 湖北 武汉 430019；3. 66136部队，北京 100043)

在反导预警系统中，目标识别是最关键、最核心的环节。弹道导弹目标识别涉及的装备种类复杂，技术含量高，易受外界环境干扰，且弹道导弹目标突防手段多样，目标环境复杂，单个传感器、单个特征难以有效完成目标识别任务[1]。因此，多传感器、多特征融合识别将是未来发展方向。多传感器融合可分为数据层、特征层和决策层[2-3]。当前，多传感器融合问题研究主要集中在决策层，如：笔者等[4]提出了一种基于证据理论(Dempster-Shafer Theory，DST)和比例冲突再分配准则5(Proportional Conflict Redistribution Rule 5，PCR5)的弹道目标识别方法，有效解决了识别中不稳定、不一致信息的融合问题；金宏斌等[5]提出了一种基于DSm(Dezert-Smarandache)理论的弹道导弹目标综合识别方法，有效解决了多传感器相互矛盾的、模糊的信息融合问题；李昌玺等[6]提出了一种基于专家系统的弹道导弹目标综合识别方法，引入专家系统理论对冲突证据和非冲突证据分别进行处理，最后通过实例验证了该方法的有效性。尽管上述研究均不同程度地解决了不一致、冲突的信息融合问题，但由于决策层融合事先对传感器的数据进行了浓缩，预处理代价高，势必会减少信息含量。因此，需要加强数据层、特征层的数据融合研究。

数据层融合虽信息利用充分，但因数据量大、运算时间长，无法满足导弹防御系统的实时性要求。特征层融合位于数据层和决策层之间，既能保证信息量，又能满足实时性，因而更适合弹道导弹目标综合识别。特征层融合的优势在于能够消除各传感器之间的冗余信息，获取维数最小、最有效的特征组合，提高目标综合识别能力。传统的特征层融合方法主要将各传感器的特征向量连接成一个长的特征向量，然后引入主成分分析(Principle Component Analysis,PCA)进行一维特征融合(one-Dimensional Feature Fusion，1DFF)，这种方法得到的特征维数较大，但无形中增加了计算量，降低了融合识别效率[7-9]。

鉴于此，笔者提出一种新的特征层融合思路，首先将多个标准化的特征向量组合成二维特征矩阵，然后引入图像压缩技术中的二维主成分分析(Two-Dimensional Principal Component Analysis，2DPCA)方法[10-13]进行二维特征融合(Two-Dimensional Feature Fusion，2DFF)识别，最后结合典型场景进行仿真实验验证。

1 2DPCA特征提取方法

假设X为n维归一化向量，将l×n矩阵B经线性变换投影到X上，即

Y=BX。

(1)

这样，则可产生一个投影向量Y,又称为矩阵B的投影特征向量(也可简称“特征向量”)。为了获得最佳的投影向量X，实际应用中用样本投影后的分散度J(X)来衡量投影向量区分样本的能力，此处用样本投影向量Y的协方差Sx的迹来表征，即

J(X)=tr(Sx)，

(2)

式中：

Sx=E(Y-E(Y))(Y-E(Y))T=

E(BX-E(BX))(BX-E(BX))T=

E((B-E(B))X)((B-E(B))X)T。

(3)

结合式(2)、(3)可得

J(X)= tr(Sx)=

XT[E(B-E(B))T(B-E(B))]X。

(4)

定义二维特征矩阵B的相关矩阵

Gt=E(B-E(B))T(B-E(B))，

(5)

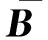
(6)

结合式(5)、(6)，Gt可表示为

(7)

由式(4)、(5)可得

J(X)=XTGtX。

(8)

式(8)被称为总体分散度准则，使得总体分散度J(X)最大的归一化向量Xopt(Gt最大特征值对应的特征向量)为最优投影轴，即所有样本二维矩阵在Xopt上的投影向量之间分散度最大。通常情况下，仅有一个最优投影轴是不够的，需要一系列投影向量组成集合{X1,X2,…,Xd}，它们彼此正交化，使得J(X)尽量最大，即

(9)

满足式(9)的投影向量集合{X1,X2,…,Xd}是Gt的前d个最大特征值对应且彼此正交的特征向量。

2 弹道导弹目标识别特征分析

在弹道导弹目标识别中，主要需要雷达和红外2种传感器，其中雷达是反导预警中的主要识别装备，因此在识别特征分析时着重考虑雷达识别特征。

目前用于弹道导弹目标识别的雷达特征有几十种，大致可以分为雷达散射面积(Radar Cross Section,RCS)特征、弹道特征、微动特征、高分辨率、一维距离像(High Resolution Range Profile,HRRP)特征、逆合成孔径雷达(Inverse Synthetic Aperture Radar,ISAR)特征、极化特征6大类[14-15]。表1给出了6大类特征及对应的描述子，其中：RCS特征不仅能大致确定目标大小，而且其起伏变化反映了目标的运动信息；弹道特征利用速度、加速度、航迹等区分真目标和有源假目标，另外在再入段利用质阻比区分真目标和重诱饵；微动特征是区分真目标和无源诱饵的重要手段；HRRP特征无需进行精细的运动补偿，即可获取目标的精细结构，然而这种特征对目标姿态敏感；ISAR特征克服了HRRP对姿态角敏感的不足，能够清晰直观地反映目标外形、轮廓、散射中心等结构信息，然而这种特征需要较长的积累时间和较高的跟踪数据率；极化特征能够提供更全面精细的识别信息，但对器件水平要求高。

表1 雷达识别特征及对应描述子

张平定等[16]研究发现：假目标仅能在某个或某几个方面模仿真弹头，无法完全模拟真弹头所有特征，且识别特征能否有效获取与装备部署位置有一定的关系。因此，综合多装备多特征进行综合识别能够有效提高目标识别率。

3 基于2DPCA的特征级综合识别流程

本文主要运用2DPCA对构造的二维特征矩阵进行主成分分析，提取新的融合特征，以对目标进行分类识别。基于2DPCA的弹道导弹目标特征级综合识别流程如图1所示，具体描述如下：

1) 信号特征提取。对各传感器的原始信号进行特征提取，同一个或不同传感器可采取不同的方法进行特征提取。

2) 特征标准化。假设有M个传感器，每个传感器对应N维特征向量，则第p个传感器的特征向量

bp=(bp,1,bp,2,…,bp,q),
p=1,2,…,M,q=1,2,…,N。

(10)

由于每个传感器一般采用不同的处理方法提取特征值，因此各特征值具有不同的量纲。为了消除这种影响，必须对各传感器的特征值进行标准化处理。笔者采用标准差进行标准化处理，具体为

(11)

将各传感器标准化处理后的特征向量作为行向量，按照一定顺序组合成的特征矩阵为

(12)

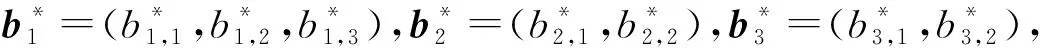
(13)

通常情况下，当每个传感器特征向量维数相近时，2DPCA才能适用，一般要求传感器特征向量维数的最小值与最大值之比≥0.8，若低于这个标准，2DPCA的优势将变弱。

3) 假设Gt的特征值为{λ1,λ2,…,λN|λ1>λ2>…>λN}，定义σq为特征值λq的贡献度因子，有

(14)

找出前D个特征值，累计贡献度满足如下关系：

(15)

其中θ值根据具体应用需求确定。将D个特征值对应的特征向量集{X1,X2,…,XD}用于二维特征矩阵的二次特征提取。根据式(1)，可以得到投影特征向量集{Y1,Y2,…,YD}，即为二维特征矩阵的主成分向量，它们组合在一起形成M×D的融合特征矩阵。

4) 针对融合获取的特征，选取合适的分类器进行目标分类识别。

4 仿真验证

鉴于弹道导弹目标的敏感性，相关试验数据主要通过仿真获取。试验场景主要设定为R1、R2、R3三部雷达，弹头、诱饵、碎片3类目标，雷达部署场景如图2所示。雷达观测位置相关数据如表2所示。

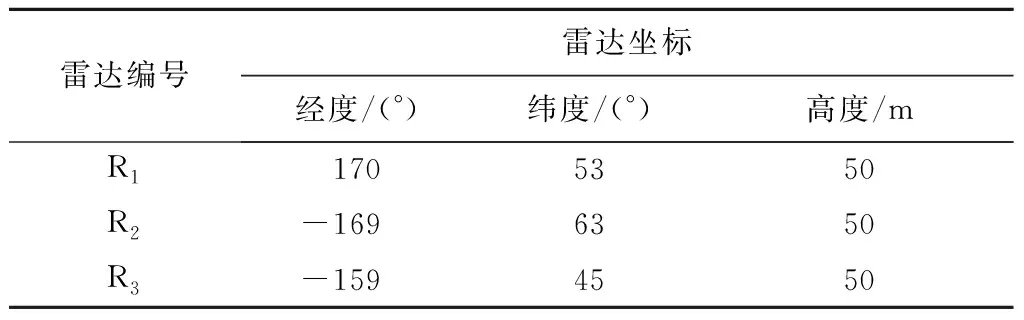
雷达编号雷达坐标经度/(°)纬度/(°)高度/mR11705350R2-1696350R3-1594550

试验主要结合仿真获取的RCS特征数据，重点提取目标RCS序列的均值、标准差、功率谱熵、极值、分布特征参数，对多装融合识别结果与单装识别结果、基于2DPCA的2DFF识别结果与基于PCA的1DFF识别结果进行了比较，并分析了维数对融合识别结果的影响。在每次试验中，将特征分为训练集和测试集，每次的训练样本都是重新选择，在分类器使用上选择最小临近分类器。

雷达部署在不同位置时目标的平均视线角如图3所示，3部雷达下不同目标的RCS序列如图4-6所示。结合图3-6可知:目标的平均视线角随着雷达部署位置而改变，每个时刻各雷达部署下目标视线角不同；受视线角变化的影响，目标的RCS大小也存在差异。因此，目标的RCS序列与装备部署位置有着直接联系。

4.1 识别结果对比

特征向量选用均值、标准差、功率谱熵，以40 s为统计区间，根据分类器识别结果统计识别率，比较多传感融合识别与单传感器识别的结果。

图7为3部雷达识别结果。可以看出：R1、R2、R3分别在760～1 000 s、1 000～1 120 s、1 160～ 1 240 s具有较高的识别率，识别率在70%以上。结合图3可以看出：在上述3个时间段，雷达的平均视线角为80°～100°，考虑到目标的微动特征，则雷达的平均视线角约为90°，此时目标侧面正对雷达，目标回波最强，弹头目标隐身性能变弱，说明此时更有利于目标识别。

图8为2DFF和1DFF两种方法的融合识别结果对比。可以看出：基于2DPCA的2DFF融合识别结果在1 320 s之前优于基于PCA的1DFF，之后劣于1DFF。这是因为：在1 320 s前，各雷达下目标视线角差异较大，采用2DFF方法相当于引入了额外的结构特征信息，这有利于目标的识别；在1 320s

后，各雷达下目标视线角差异较小，结构特征信息不易获取，且此时目标距离较远，回波弱，采用1DFF方法将多个特征向量组成一个长的特征向量，在分类识别时多个特征量的差异积累，反而有助于目标分类识别。

结合图7、8可以看出：2种方法融合后的识别率总体上高于单部雷达。

为对比2DFF和1DFF两种方法的运算效率，共进行了500次仿真试验。结果表明：2DFF方法的平均运算时间为0.017 45 s，1DFF方法的运算时间为0.068 06 s，即2DFF方法的运算效率高于1DFF方法，是后者的3.9倍。这是由于1DFF方法需要计算维数(3×3)2的相关矩阵，而2DFF方法只需要计算维数32的相关矩阵。

4.2 特征向量维数的影响

考虑特征向量维数变化对目标识别的影响，其特征向量主要由均值、标准差、功率谱熵、极值、分布特征参数等组成，重点统计760 ～1 240 s区间内的目标识别率。

表3为不同特征向量维数下2DFF和1DFF两种方法的融合识别结果对比。可以看出：2DFF方法的融合识别率高于1DFF方法，且与特征向量的维数无关，这说明并不是特征向量维数越大，目标识别效果越好。分析其原因为：随着维数的增加，分类器结构更加复杂，识别性能下降。因此，为得到最优识别性能，需要合理选择特征向量维数。

表3 不同特征向量维数下2DFF和1DFF两种方法融合识别结果对比

4.3 融合识别方法的影响

采用与4.2节相同的特征向量，考虑雷达特征向量维数不同时，2DFF和1DFF两种识别方法对目标识别的影响。其中，因极值易受噪声影响，删除R1的特征极值，将余下的4个特征构成特征向量，其他2部雷达的特征向量不变。这样，有1个4维特征向量和2个5维特征向量，特征向量维数的最小值与最大值之比≥0.8。在组合特征前，首先对特征向量进行维数配准，即在特征向量后面加0，使向量维数为5。

表4为2DFF和1DFF两种方法融合识别结果对比。可以看出：当特征向量维数不一致时，2DFF方法的识别率更高，且优于1DFF方法。

表4 2DFF和1DFF两种方法融合识别结果

5 结论

为有效提高弹道导弹目标多传感器综合识别的正确率，笔者提出了一种基于2DPCA的弹道导弹目标特征级融合识别方法，并通过仿真试验验证了该方法的有效性。结果表明：该方法能获得较高的识别率，且计算复杂度较低。在该方法中，特征矩阵的相关矩阵获取尤为关键，如何在有限训练样本下获取精确的相关矩阵将是下一步重点研究方向。