函数中常见的易错点

■河南省光山县第二高级中学 史厚芝

函数是高中数学的重要知识内容,是高中数学知识的一条主线,是高考的重点和热点。数、式、方程、函数、排列组合、数列等都是以函数为中心的代数,高考试题中始终贯穿着函数及其性质这条主线。然而,在学习中,很多同学对函数的内容经常会出现某些模糊的认识。

警惕1——求函数定义域时忽略定义

A.(1,2] B.[1,2]

C.(1,2) D.[2,+∞)

易错防范：(1)求函数的定义域时,关键是依据含自变量x的代数式有意义来列出相应的不等式(组)求解,列不等式时,应列出所有的不等式,不要遗漏。(2)对于复合函数求定义域问题,若已知f(x)的定义域为[a,b],则复合函数f(g(x))的定义域由不等式a≤g(x)≤b得到。(3)对于实际问题或几何问题,此时除要考虑解析式有意义外,还应考虑使实际问题或几何问题有意义。

易错点：求解复合函数的定义域问题时要注意定义。

警惕2——求复合函数单调性与应用函数单调性时忽略定义域

剖析：此题考查同学们对幂函数及二次函数图像和性质的研究能力,以及会求复合函数的增减性的能力。在完成此类题目时,一些同学往往只会抓住复合函数单调性的规律:“同增异减”,而不考虑函数的定义域,进而得出错误的结果。

易错防范：(1)求复合函数的单调区间时,切勿只顾及内层函数的单调区间,而忽视了函数定义域的重要性。(2)解决抽象不等式f(a)＜f(b)时,切勿将自变量代入函数解析式进行求解,首先应该注意考察函数f(x)的单调性。若函数f(x)为增函数,则a＜b;若函数f(x)为减函数,则a＞b。

跟踪训练2 已知f(x)是定义在[-1,1]上的奇函数,若a,b∈[-1,1],a+b≠0立。

(1)判断f(x)在[-1,1]上的单调性,并证明;

正解：(1)任取x1,x2∈[-1,1],且x1＜x2,则-x2∈[-1,1]。

因为f(x)为奇函数,所以f(x1)-(x1-x2)。

易错点：第(2)问没注意到定义域会出错。

警惕3——判断函数奇偶性时忽视定义域

错解:非奇非偶。

剖析：如果不在定义域下化简,而直接去绝对值得到分段函数,就会导致判断出错。定义域为(-1,0)∪以f(-x)=-f(x),故f(x)为奇函数。

易错防范：(1)判断函数的奇偶性,先要注意定义域必须关于原点对称,有时还要对函数式化简整理,判断时必须注意使定义域不受影响。(2)化简后再用f(-x)=f(x)或f(-x)=-f(x)来判断。

跟踪训练3 已知函数f(x2-1)=判断f(x)的奇偶性。

易错点：此类题型常犯的错误是不先考虑定义域,直接运用换元的方法求解。

警惕4——要弄清函数奇偶性的性质

例4 已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增。若则a的取值范围是( )。

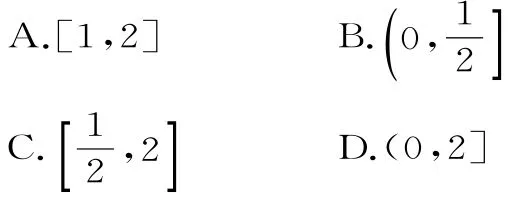
剖析：(1)该例在求a的取值范围时,应根据题中的条件利用函数的单调性和奇偶性去掉对应法则。(2)由f(x)是定义在R上f(l o g2a),该不等式可化为f(l o g2a)≤f(1),再由函数f(x)在区间[0,+∞)上单

易错防范：(1)奇函数在关于原点对称的区间上若有单调性,则其单调性完全相同;偶函数在关于原点对称的区间上若有单调性,则其单调性相反。(2)若f(x)为偶函数,则f(-x)=f(x)=f(|x|)。(3)若奇函数f(x)的定义域中含0,则必有f(0)=0。故“f(0)=0”是“f(x)为奇函数”的既不充分也不必要条件。特别要注意用f(0)=0求函数解析式中参数的值时可能造成漏解的情况。

A.1 B.-1 C.±1 D.0

正解：因为f(x)是奇函数,所以f(-x)=-f(x),即f(-x)+f(x)=0,所k=±1。故选C。

易错点：由于直接用了f(0)=0造成漏解而出错。

警惕5——处理分段函数问题时的思路和方法不妥

错解:因为对任意x1≠x2,都有立,所以f(x)是减函

剖析：分段函数的单调性问题是容易出错的问题,有些同学由于缺少整体意识,错解这种错误解法的原因是忽视了函数图像是不连续的,没有注意端点值的情况。根据图像

易错防范：解答分段函数问题的重要途径是数形结合,画出函数的大致图像,定义域、值域、最值、单调性、奇偶性等问题就会迎刃而解;方程、不等式可用数形结合思想、等价转化思想、分类讨论思想及函数思想来解决,使问题简化,效果明显。

易错点：把不等式问题转化为函数问题来处理时,分类讨论是易错点。

警惕6——用换元法、均值不等式求值域时易忽视定义域的变化

剖析：换元法是求解不等式、函数最值等问题的重要方法之一,使用这种方法解题常常能把复杂式子简单化。但是在使用换元法解题时要特别注意新元与旧元之间转化的等价性,否则容易出错。错解的原因是没有注意原函数的定义域要满足t=s i nx+c o sx≠-1,所以y≠-1,所以原函数的值域为

易错防范：(1)在用换元法解题时,要知道新函数的定义域会随着变量的转换而变化,所以在换元的过程中,要同步确定新元的取值范围,而不能仅由新函数的结构性质来确定。(2)如果换元后用均值不等式,要注意取等号的条件;若不满足条件还需用函数的单调性来求。

易错点：换元后用均值不等式,不满足取等号的条件。

警惕7——二次函数中含字母参数问题的等价转化

例7 设函数f(x)=x2-a x+b(a,b∈R)。

(1)若f(x)在区间[0,1]上的最大值为b,求a的取值范围;

(2)若f(x)在区间[1,2]上有零点,求a2+2b2-4b的最小值。

错解:(1)分类讨论对称轴与区间的3种位置关系求最值后再求a的取值范围时易出错。(2)等价转化是本题难点也是易错点。

剖析：(1)利用抛物线的几何特征易知在区间[0,1]上的最大值必是f(0)和f(1)中的较大者,而f(0)=b,所以只要f(0)≥f(1)即可。

(2)因为f(x)在区间[1,2]上有零点等价于方程x2-a x+b=0在区间[1,2]上有根,设方程x2-a x+b=0的两根是x1,x2,且1≤x2

易错防范：(1)求解含字母参数的二次函数指定区间最值问题,首先利用抛物线的几何性质来求,不行再考虑讨论对称轴与区间的位置关系来求。(2)遇到二次函数零点问题可以用根的分布,也可考虑对应的二次方程根与系数的关系。

跟踪训练7 若函数g(x)=2x2+a x+3在区间(1,2)上有两个不同的零点,求实数a的取值范围。

正解：函数g(x)=2x2+a x+3在区间(1,2)上有两个不同的零点,则

易错点：判别式易漏。

警惕8——关于对数、指数函数求参数问题中端点值的处理

例8 若关于x的不等式4ax-1＜3x-4(a＞0,且a≠1)对于任意的x＞2恒成立,则a的取值范围为( )。

错解:易错选A。

剖析：本题是不等式恒成立求参数的取值范围问题,常见的处理方法有:常变量分离、考查不等式对应的函数、数形结合。

易错防范：(1)遇到不等式恒成立求字母参数问题时,首先等价转化找到适当的解题方法,常见的处理方法有:常变量分离、考查不等式对应的函数、数形结合。(2)指、对数式中底数为字母的应分类讨论底数a＞1或0＜a＜1两类。(3)对数式中真数大于零。

跟踪训练8 已知函数y=l o ga2(x2-2a x-3)在(-∞,-2)上是增函数,求a的取值范围。

正解：令μ(x)=x2-2a x-3在(-∞,a]上是减函数,在[a,+∞)上是增函数,所以要使y=l o ga2(x2-2a x-3)在(-∞,-2)上是增函数,首先必有0＜a2＜1,且(-∞,综上所述,a 的取值范围是

易错点：(1)题意的等价转化;

警惕9——幂函数与指数函数在比较大小题型中易混淆

A.b＜a＜c B.a＜b＜c

C.b＜c＜a D.c＜a＜b

错解:有些同学搞不清是用幂函数还是指数函数的性质来比较,易错选B,C,D。

易错防范：(1)指数函数和幂函数的性质混合应用时很容易混淆,首先必须分清是底同还是幂同,若是底同应用指数函数的单调性质比较大小,若是幂同应用幂函数的单调性质比较大小。(2)在利用性质时最好结合函数图像。

跟踪训练9 若-1＜a＜0,试比较3a,

正解：由-1＜a＜0,考察指数函数y=3a,y＞0,所以3a＞0。再考察幂函数y=a3,-1＜a＜0,所以0＜-a＜1。设f(x)=(-a)x,则f(x)在x∈R时单调递减,故0＜

易错点：指数函数和幂函数的性质混合应用时很易混淆。