子母式穿梭车仓储系统复合作业路径优化
2018-10-18李国栋
杨 玮,岳 婷,李国栋,王 婷,刘 江
(陕西科技大学 机电工程学院,陕西 西安 710021)
0 引言
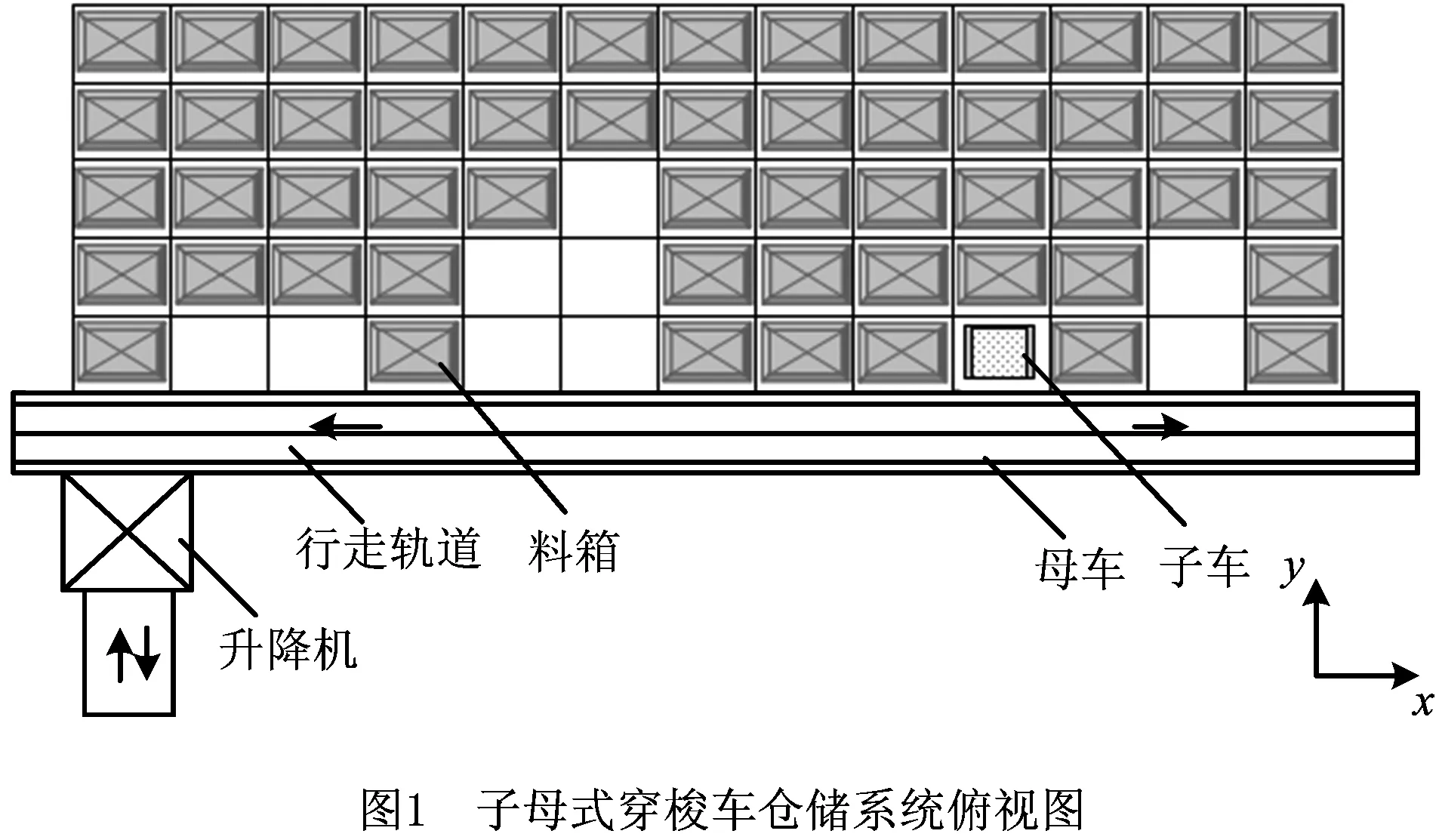
在互联网技术的推动下,我国电商企业快速发展,而支撑电商企业发展需要强大的物流仓储系统。因此,采用先进的仓储系统优化理论、方法和手段,运用新技术解决物流仓储瓶颈问题具有重要的理论和现实意义。子母式穿梭车仓储系统(Shuttle-Carrier Warehousing System, SCWS)是一种集仓储、配送、管理等功能于一体的新兴密集存储系统,主要由穿梭子车、穿梭母车、行走轨道、巷道货架、垂直输送机、托盘输送系统、无线控制系统(Wireless Control System, WCS)、仓储管理系统(Warehouse Management System, WMS)等组成。货物和穿梭母车通过升降机进行换层运动,穿梭子车通过母车的接载实现货物的进出库流转。该系统库容量大、集成度高、可扩展性强,在烟草、医药及冷链物流等行业具有广泛的用途。进出库复合作业是子母式穿梭车仓储系统一种常用作业方式,采用合理的调度策略是提高系统吞吐性能的有效手段,而这在很大程度上取决于系统执行复合作业的路径是否合理。
目前,国内外学者对于自动化立体仓库作业调度的研究,大多集中在堆垛机式仓储系统中的固定货架。例如:蔡安江等[1]以堆垛机执行任务所需总时间为评价标准,建立了适用于多出/入库台情况下的堆垛机调度路径模型;陈璐等[2]针对自动化立体仓库中物料储位分配问题,考虑动态储位分配的耗时和堆垛机行驶能力的限制,设计了两阶段启发式算法以最小化再分配操作总耗时,结果表明该算法具有较好的鲁棒性;陈旻等[3]以订单总拖期最小化为目标建立了两阶段混合流水调度模型,通过实例分析选取合适的启发式规则组合,设计了两阶段的禁忌搜索算法从而快速计算出堆垛机的优化调度方案,计算结果证明了算法的可行性与有效性;黄伟[4]根据双倍货架是否存在空位建立了堆垛机式双载物平台随机存储下的时间模型,将利用缓冲区间翻箱和利用载物平台翻箱的时间进行对比,表明系统运行时间随着货位利用率的增大而增大;Drazěn等[5]在分类存储的基础上,分别采用最近邻法、最近邻插入法、最短腿和遗传算法求解三载具堆垛机式自动化立体仓库进出库复合作业问题,结果表明遗传算法结果优于其他启发式算法;Yang等[6]研究了在存取货位可共享的双载具自动化立体仓库的进出库复合作业,并采用一种可变邻域搜索的方法进行求解,最后分析了算法中各个参数的调整对算法效率的影响;Azzi等[7]提出一种蒙特卡洛分析方法来确定堆垛机的行程时间,并通过实际工业应用验证了方法的有效性。
虽然单台堆垛机即可在水平和垂直方向同时运动,但相对于现今兴起的提升机与穿梭车配合作业方式,其效率仍有待进一步提高。为适应多层穿梭车式仓储系统的发展,近年来国内外学者也进行了一些研究。Tone等[8-9]分别对单深式货架和倍深式货架的多层穿梭车立体仓库在单倍命令周期和双倍命令周期下的的行程时间进行了建模,并与实际测试数据进行对比,验证了模型的准确性;牟善栋[10]以单深式多层穿梭车仓储系统中任务出库时间、提升机空闲时间和穿梭车等待时间最小为目标建立了任务单一出库模型,并采用带精英策略的非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm-Ⅱ, NSGA-Ⅱ)对其进行求解,以实例验证了模型及算法的有效性;Carlo等[11]对在多个巷道可共享使用两个提升机的多层穿梭车立体仓库进行了研究,以进出库作业时间最短为目标函数建立调度模型,确定了两个提升机的调用顺序,并将实验结果与提升机1∶1配比下的实验结果进行比较,验证了模型的优越性;郭红丽[12]介绍了每层一台穿梭车和m层n台穿梭车两种形式的自动化立体仓库,对立体仓库的拣选作业进行分析,结果表明m层n台模式的经济成本比每层一台模式大幅降低,同时时间成本在可接受范围之内。对于路径优化问题,张丽艳等[13]提出将粒子群优化算法与模拟退火算法结合的混合粒子群算法,以求解带时间窗的车辆路径优化问题,通过实例验证该算法是一种求解离散优化问题的有效算法;高尚等[14]提出结合不同交叉变异策略的混合粒子群算法求解旅行商问题,算法简单有效,适用于求解各种组合优化问题;方彦军等[15]研究了自动小车存取系统的复合作业三维空间路径优化问题,采用改进的人工狼群算法求解,并验证了算法的有效性。
在已有涉及多层穿梭车式仓储系统进出库调度问题的研究中,所使用的穿梭车多为往复式直行穿梭车或环形穿梭车,对于近年来兴起的子母式穿梭车仓储系统三维空间复合作业路径规划鲜有研究。同时,目前国内关于多层穿梭车的应用尚停留在每层每巷道一台穿梭车的阶段,企业前期投资成本较大,当订单量较小时,多数穿梭车处于闲置状态,易造成资源浪费。
本文从作业排序、作业路径的角度,以子母式穿梭车仓储系统进出库复合作业为研究对象,对两套子母车配一台升降机的作业路径优化问题进行研究。建立了SCWS进出库复合作业调度模型,采用自适应粒子群算法分别对30,50,100个作业对的进出库作业路径问题进行求解,并与升降机与子母穿梭车1∶1配比方式下的作业时间进行对比,力求在接近作业实际的角度下最小化进出库作业的总行程时间,提高存取作业效率。
1 SCWS中路径优化问题的描述及建模
1.1 问题描述
以某储存设备公司生产的SCWS为例,其俯视图与示意图分别如图1和图2所示。输送系统由一台垂直升降机和两套子母车系统构成。结合具体的进出库任务,该SCWS的作业流程为:
(1)入库作业 升降机载着入库任务的子母车输送到相应的入库货位所在层,释放母车,由母车将子车运送到相应的入库列后释放子车,子车将料箱运送到入库点,释放料箱,完成入库作业。
(2)出库作业 执行出库任务时,升降机载着子车的母车运送到出库货位所在层,释放母车,由母车将子车运送到相应的出库列后释放子车,子车将料箱运出,再经子车、母车和升降机的配合将货物送到I/O台。
当系统完成任务分配后,如何使升降机和两套子母穿梭车合理配合、高效完成订单任务,是子母式穿梭车仓储系统调度优化的目的。因此,需要对升降机和子母穿梭车的作业路径进行规划,并对执行进出库作业的两套子母穿梭车进行合理分配,而建立合理正确的复合作业调度模型是系统路径优化的关键。

1.2 模型建立
根据SCWS运行现状,提出如下假设:
(1)每列货架中均存放同种货物,采用分类存储原则。
(2)执行入库任务时,垂直升降机将一套子母车(A车)送至货物所在层出口位置,子母车执行入库(出库)作业,任务完成后在完成任务的位置等待系统指令。若垂直升降机空闲,则子母车和升降机同时运动,完成入库(出库)作业。
(3)一次进出库复合作业中,入库与出库货物位置已知。
(4)垂直升降机、子车、母车均为匀速行驶。
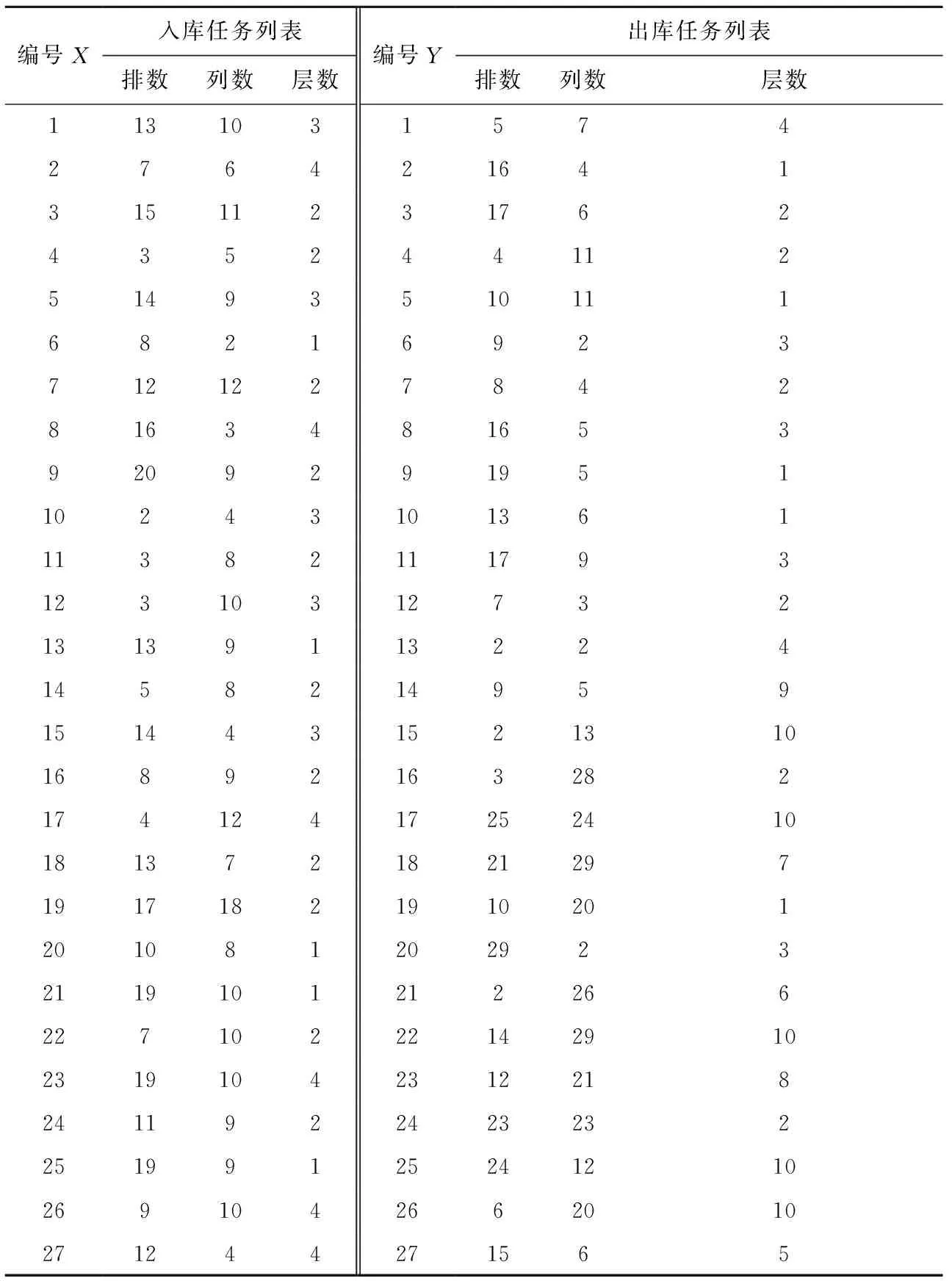
本文研究的SCWS的规格具体为10层、30排、100列,货架基本参数如表1所示。

表1 货架基本参数表
基于以上假设,从SCWS的进出库复合作业方式出发建立数学模型。两套子母车执行进出库复合作业,货架的初始状态为子车所在坐标位置(0,0,0)和(xj,yj,zj)。其中,(xj,yj,zj)为上次存放货物j的货位坐标,母车所在坐标位置为(0,0,0)和(xj,0,zj),垂直升降机位于I/O位置,坐标为(0,0,0)。按照一个存取对中,负责入库、出库任务的子母穿梭车和待出库任务所在货位的具体位置,分3种情况进行讨论:
(1)负责入库作业的穿梭车与待出库任务处于同一层,即zi=zk,如图3所示。
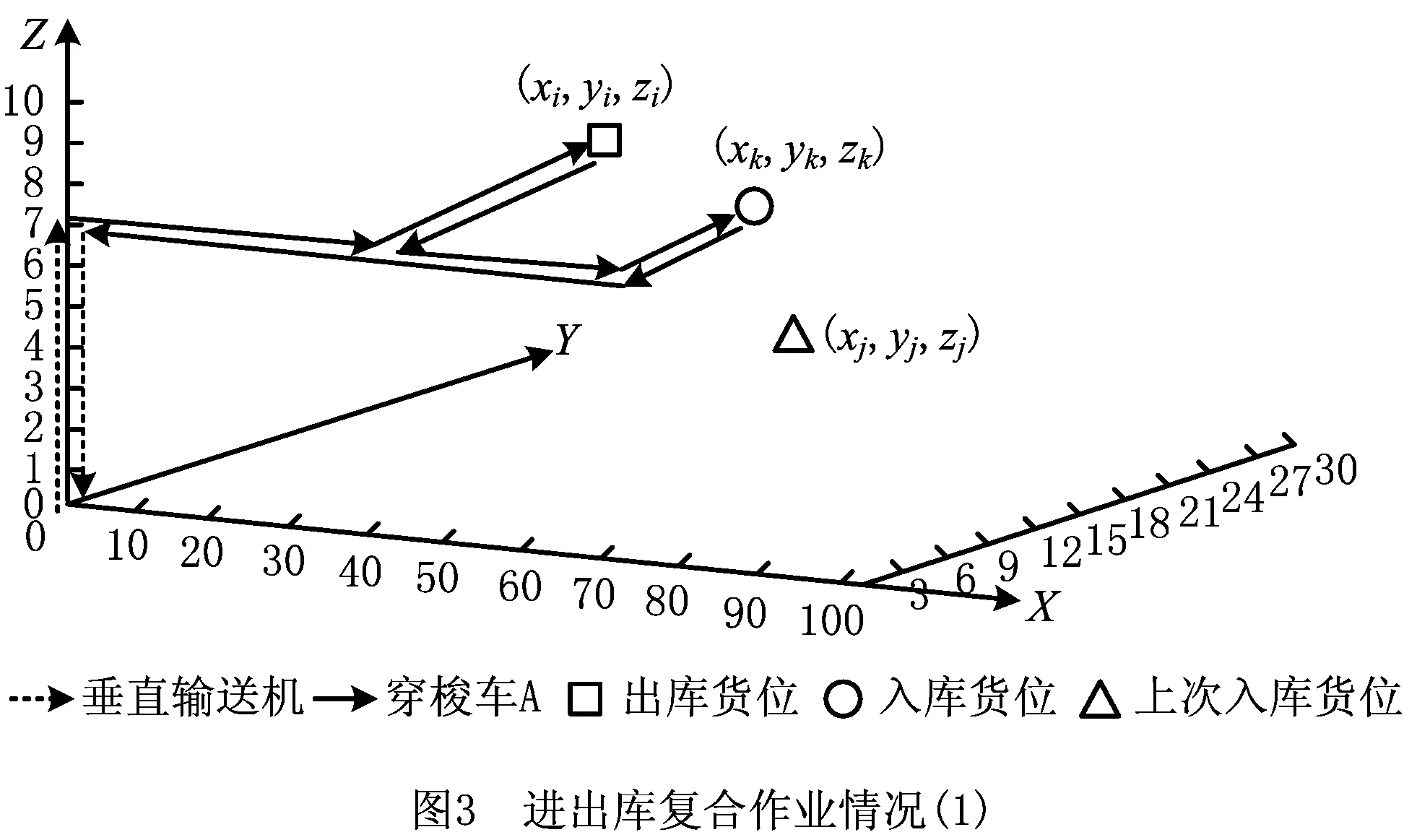
完成一次进出库复合作业的时间为TDtk1,
4tz+2ts2+2tm1+2tm2。
(1)
(2)负责出库作业的穿梭车与待出库任务处于同一层,即zj=zk,如图4所示。

完成一次进出库复合作业的时间为TDtk2,
(2)
(3)负责入库、出库以及待出库任务均不处于同一层,如图5所示。
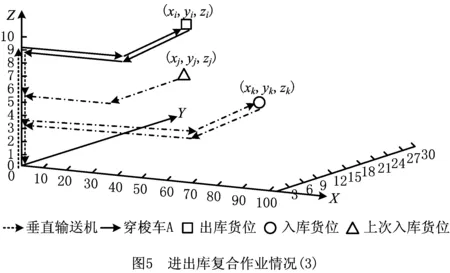
完成一次进出库复合作业的时间为TDbk,
(3)
若总共有m个存取对,一次存取作业的作业时间为TD,则当入库货位层Zi与待出库货位层Zk相等时,其存取作业时间TD=TDtk1;当出库货位层Zj与待出库货位层Zk相等时,存取作业时间TD=TDtk2;当入库、出库以及待出库任务均不处于同一层时,存取作业时间TD=TDbk,如式(4)所示。两套子母车一次作业的时间为m个存取对进行作业的时间和,即T,如式(5)所示。
(4)
(5)
2 算法描述
进出库复合作业的调度问题是一个NP-hard问题[16],本文设计混合粒子群优化(Hybrid Particle Swarm Optimization, HPSO)算法进行求解。粒子群优化(Particle Swarm Optimization, PSO)算法是借鉴动物集群活动行为,利用个体对信息的共享,驱动群体在解空间中从无序到有序的演化过程,PSO中粒子的速度和位置更新方式决定了算法初期全局寻优能力较强,后期易陷入局部最优。遗传算法(Genetic Algorithm, GA)通过模仿自然界的选择与遗传的机理来寻找最优解,其所使用的“按概率随机选择”方法能够避开其他最优化算法常遇到的局部最优问题。因此,在PSO中以一定的概率融入遗传算法的交叉和变异算子,构成混合交叉变异PSO算法,可以在PSO后期通过交叉和变异不断产生新解,避免PSO过早收敛。HPSO算法的设计和具体问题关系密切,下面对HPSO算法求解子母式穿梭车仓储系统进出库复合作业的关键技术进行说明,并给出算法流程。
2.1 编码
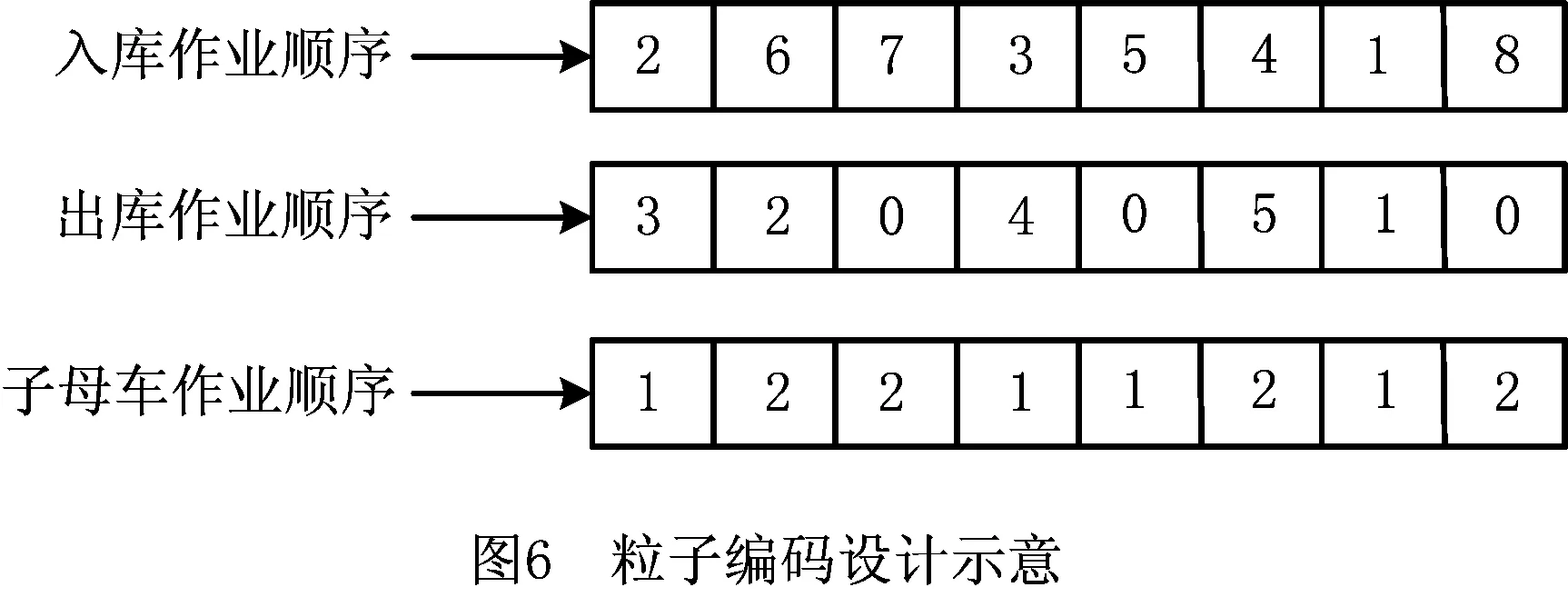
基于SCWS调度模型的特点,采用出入库混合整数编码方式。两套子母车编号集为M={1,2},将X个入库货物和Y个出库货物分别从1~X,1~Y随机编号,若X≠Y,则利用I/O位置编号“0”将任务对补齐,其中I/O位置坐标为(0,0,0),此时该任务对执行单一出库(入库)作业。
例如,存货作业编号集X={1,2,3,4,5,6,7,8},取货作业编号集Y={1,2,3,4,5},一个可行的粒子编码方式如图6所示。优化后的存货作业、取货作业与子母车调用编码顺序为[(2,6,7,3,5,4,1,8),(3,2,0,4,0,5,1,0),(1,2,2,1,1,2,1,2)]。即子母式穿梭车仓储系统以2-3,6-2,7-0,3-4,5-0,4-5,1-1,8-0这8个任务对的形式执行联合进出库调度作业,两套子母车调用顺序为(1,2,2,1,1,2,1,2),其中任务对中包含0的为单独入库作业。
2.2 适应度函数
本文的优化目标为完成订单内所有进出库作业的时间最小,则适应度函数为
(6)
2.3 SCWS调度模型的HPSO算法步骤
基于以上编码方式,为较大程度地降低HPSO算法为提高求解精度而降低求解效率的影响,在算法设计时,对交叉和变异算子采用概率交叉和概率变异的方式,算法流程图如图7所示。

算法的具体步骤如下:
步骤1初始化种群和参数。
步骤2计算适应度值并记录个体最优值和全局最优值,适应度函数所计算的个体适应度值为执行一次订单任务的总时间。
步骤3根据速度和位置更新公式[17]更新速度和位置,粒子速度更新公式为
(7)
位置更新公式为
(8)
式中:d为寻优空间,即进出库复合作业对的数量;t为迭代次数;ωt为惯性因子[18],
ωt=ωstart-(ωstart-ωend)×t/tmax;
(9)
c1,c2为学习系数;r1,r2为(0,1)之间的随机数;pi,pg为个体极值和全局极值,即个体最优作业时间和全局最优作业时间。
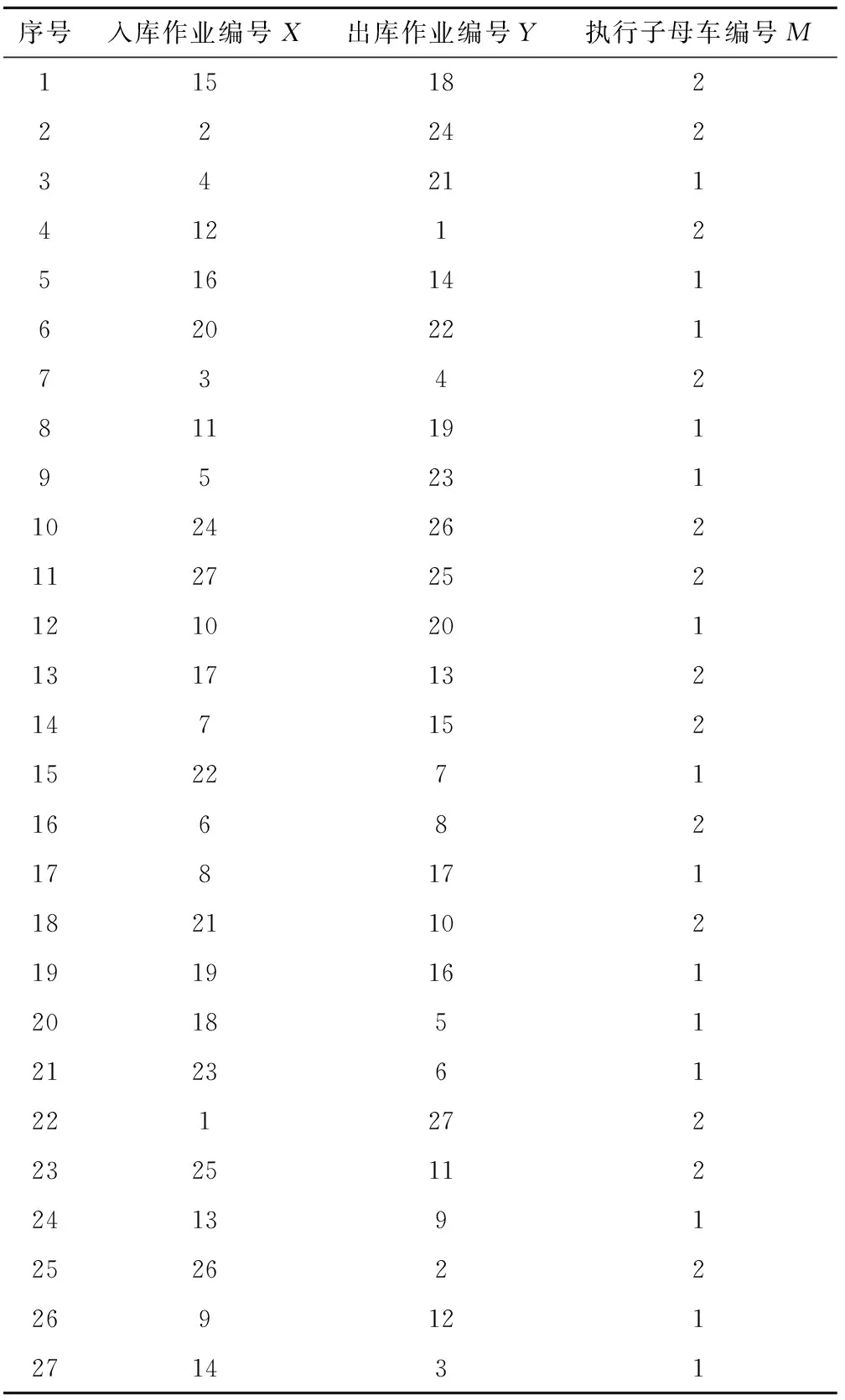
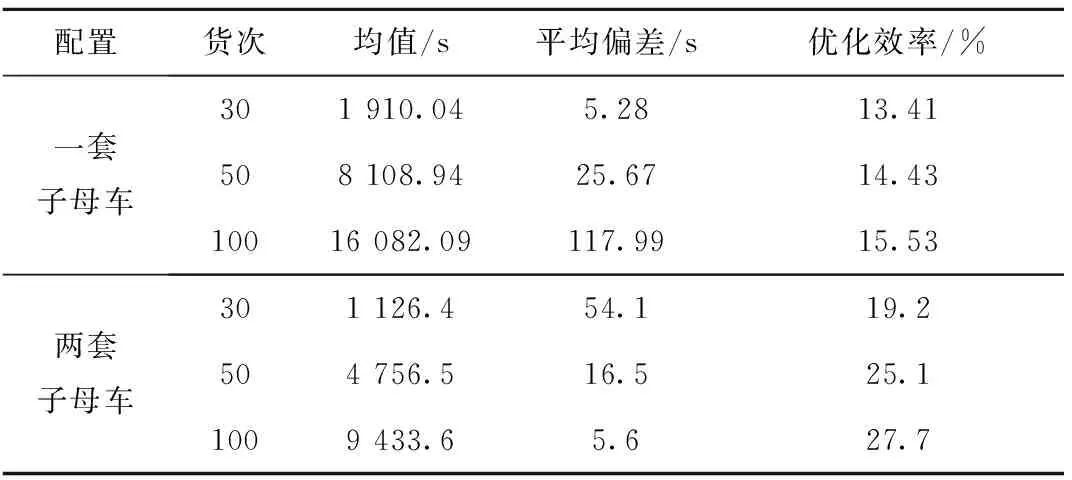
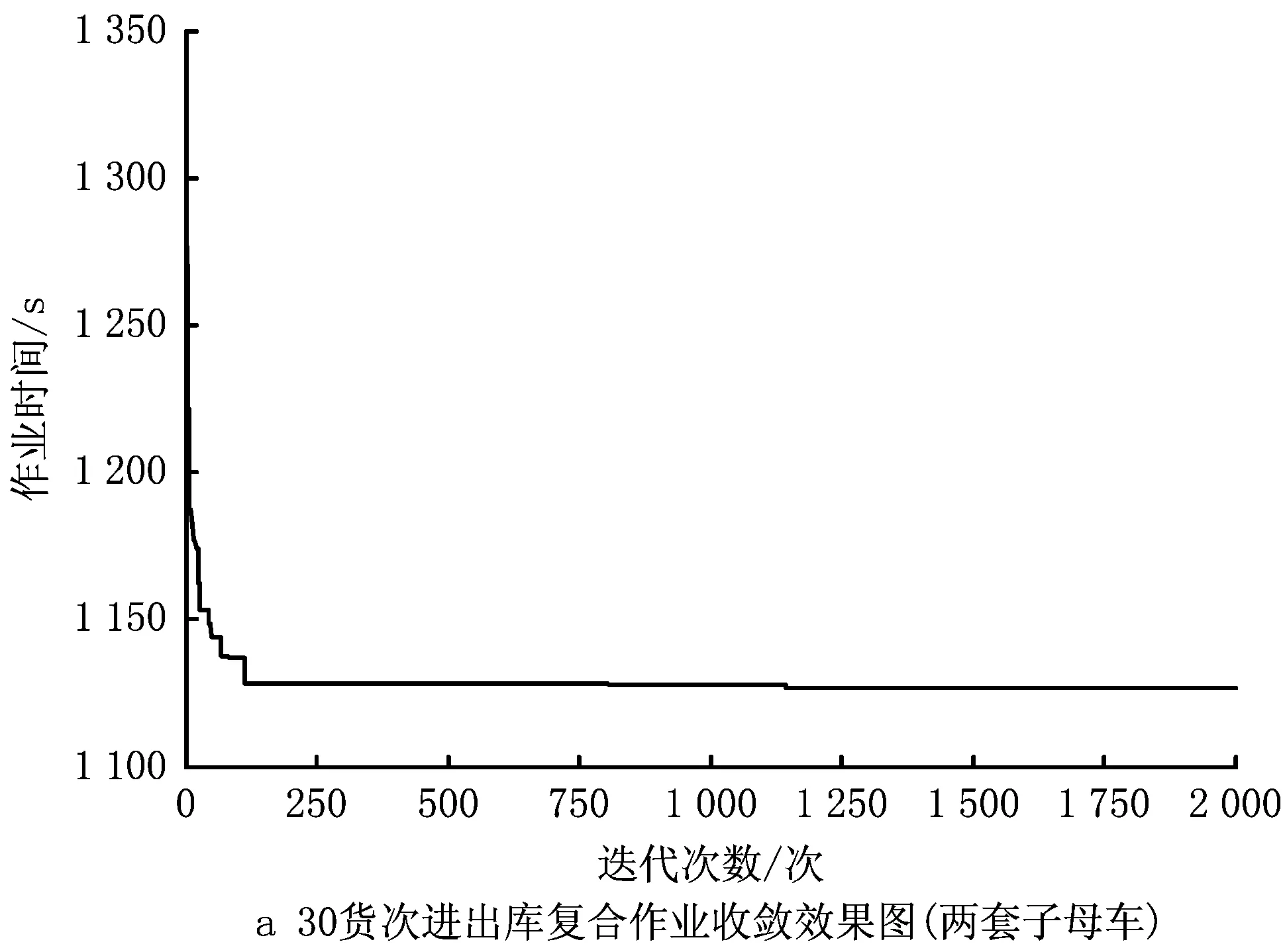
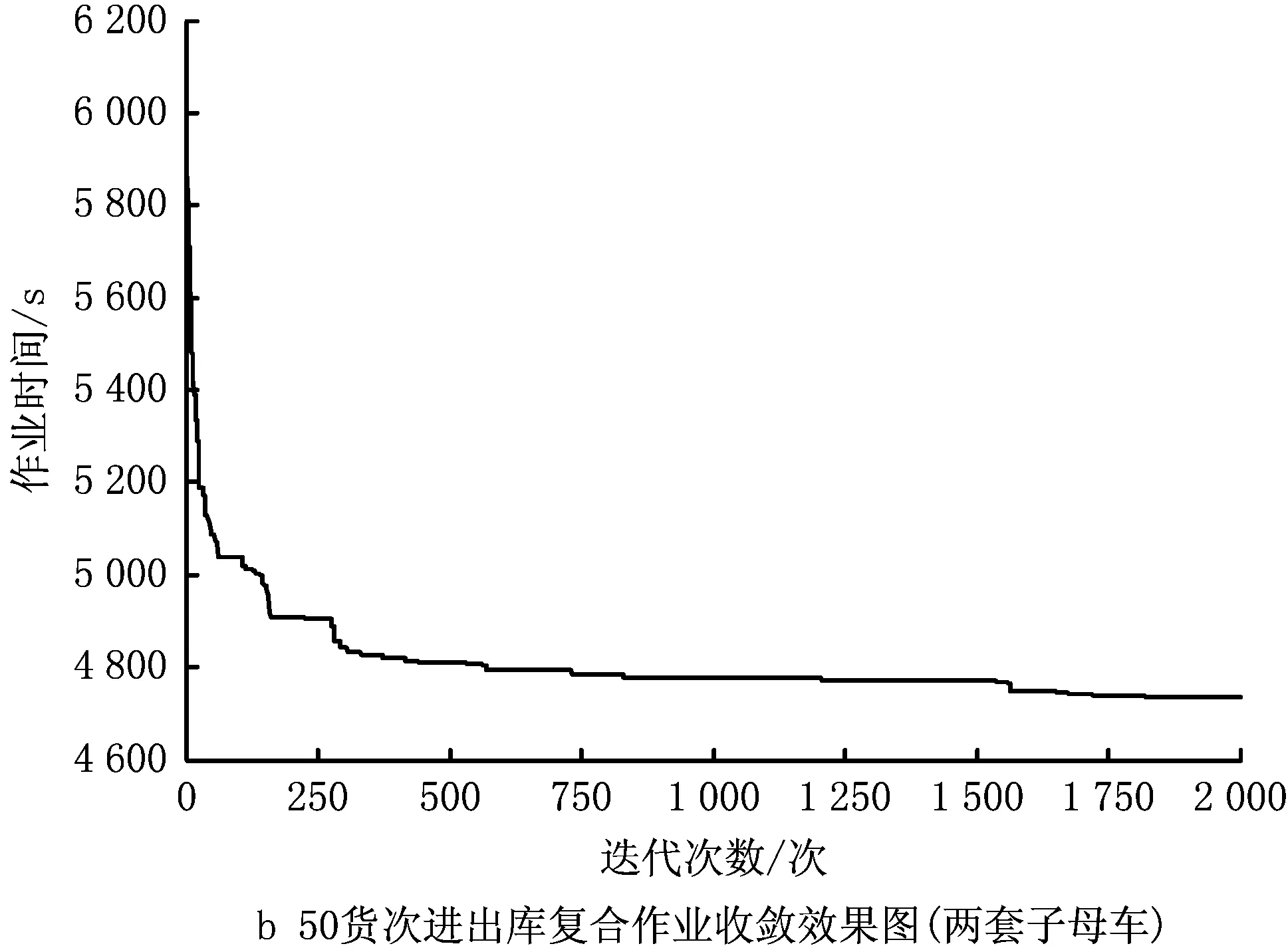
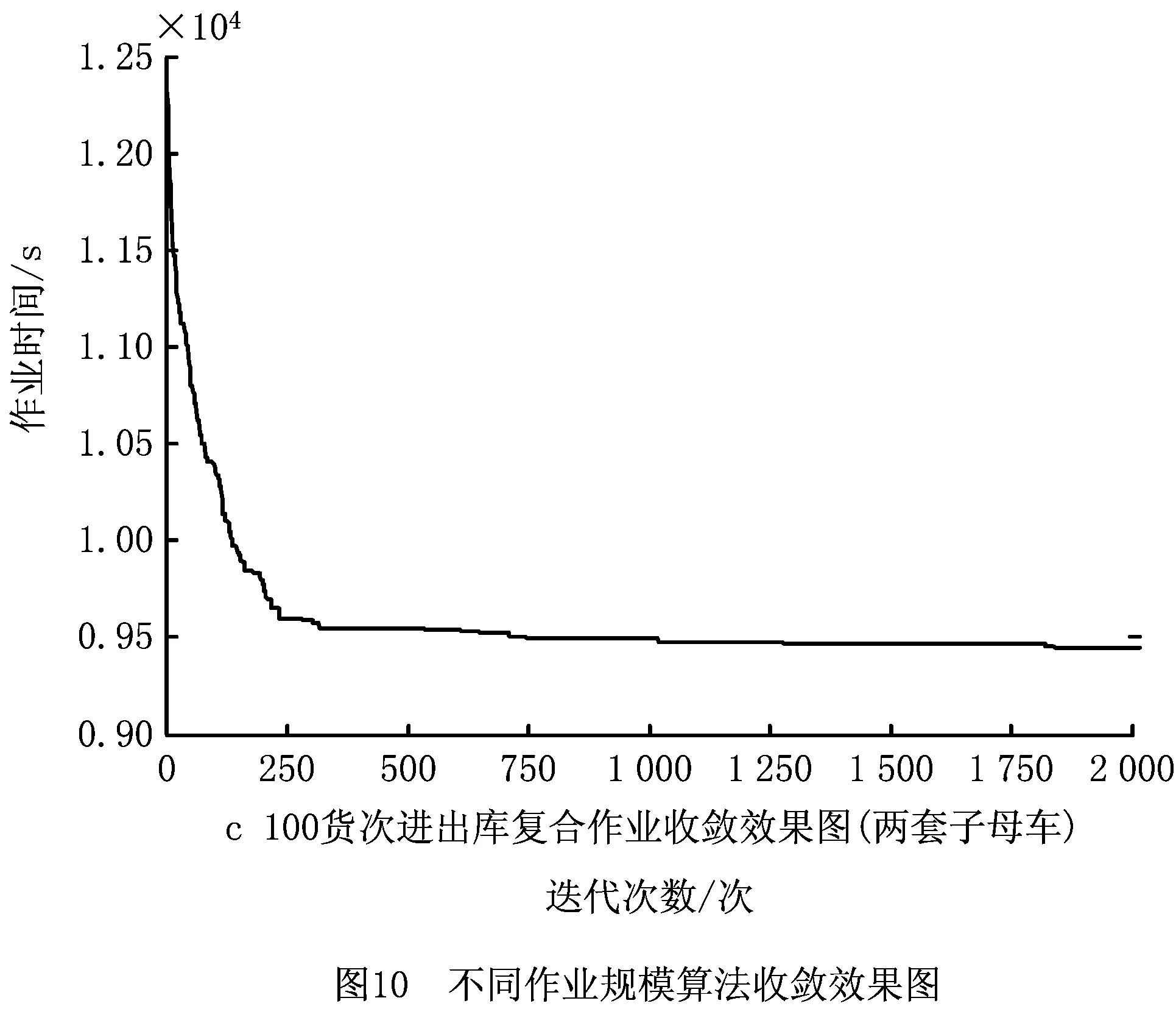
步骤4采用部分匹配交叉方法随机产生两个交叉点,定义两点之间的部分为匹配区域,若rand 步骤5为增强算法全局性,若rand 步骤6更新个体极值和全局极值。 步骤7判断算法是否结束,若不结束,则返回步骤2,继续迭代;若结束,则输出最优解。 为对SCWS进出库复合作业在不同任务量的情况进行分析,设计具有不同参数场景的问题进行数值实验。具体的参数设置为:c1=c2=2,ωstart=0.9,ωend=0.4,tmax=2 000。 以系统执行一次27任务对进出库作业为例,其中入库数为27,出库数为27。进出库任务列表如表2所示。 表2 进出库任务列表(27货次) 根据程序随机得到一组进出库复合作业路径顺序为(22-3)→(6-24)→(3-6)→(16-20)→(11-12)→(7-17)→(17-23)→(14-11)→(8-8)→(5-7)→(21-27)→(25-1)→(27-25)→(26-2)→(19-18)→(15-13)→(1-10)→(23-4)→(2-14)→(4-16)→(18-26)→(24-15)→(13-21)→(9-19)→(20-5)→(10-22)→(12-9)。作业时间为Rtime=1 209.4 s。 经过HPSO算法优化后得到一组进出库复合作业路径顺序为(15-18)→(2-24)→(4-21)→(12-1)→(16-14)→(20-22)→(3-4)→(11-19)→(5-23)→(24-26)→(27-25)→(10-20)→(17-13)→(7-15)→(22-7)→(6-8)→(8-17)→(21-10)→(19-16)→(18-5)→(23-6)→(1-27)→(25-11)→(13-9)→(26-2)→(9-12)→(14-3),相应执行任务顺序及子母车号如表3所示。总作业时间为Rtime=1 018.3 s,优化效率提高15.8%。优化后三维空间复合作业路径图如图9和图10所示。 表3 优化后作业及子母车执行顺序表 表4所示为pc=0.8,pm=0.2时,HPSO算法在不同规模与不同数量子母穿梭车的进出库复合作业情况下所优化的系统作业效率。因为一套子母车的作业方式不涉及复杂的子母穿梭车调度过程,所以直接给出计算结果。实验结果表明,在不同订单规模下,两套子母车与升降机配合作业的优化效率明显高于子母穿梭车与升降机1∶1的作业方式,并且随着问题规模的增大,优化效率进一步提高。 表4 HPSO算法在不同规模问题下的实验结果 图10所示为两套子母车在不同订单规模下的算法收敛效果图。可以看出,HPSO在迭代初期求解效率较高,同时能够不断探索新解,在交叉和变异策略下,不断跳出局部最优。在不同的订单规模下,算法求解精度均较高,稳定性较好。 本文基于SCWS进出库作业调度问题,重点研究了两套子母穿梭车配一台升降机模式下仓储系统作业调度路径模型。主要贡献如下: (1)基于对系统作业流程的分析以及两套子母车配一台升降机的进出库作业特点,以作业时间最短为目标函数,建立了适用于SCWS的进出库复合作业调度模型。 (2)设计了HPSO算法对所建立的复合作业调度模型进行路径优化求解,对两套子母穿梭车的配合作业进行优化调度。通过实例仿真验证了所建模型的准确性、复合作业调度路径优化的有效性以及两套子母穿梭车配一台升降机运作模式的高效性。 若增加升降机与子母穿梭车的数量,则作业效率将得到进一步提高,但考虑到不同生产企业对自动化立体仓库系统的能耗要求和仓储配置投资成本的不同,下一步可以针对子母穿梭车和升降机的合理配置进行研究,在最大化提高仓储系统吞吐性能的同时,降低系统能耗和企业投资成本,以使SCWS路径调度模型更具适用性。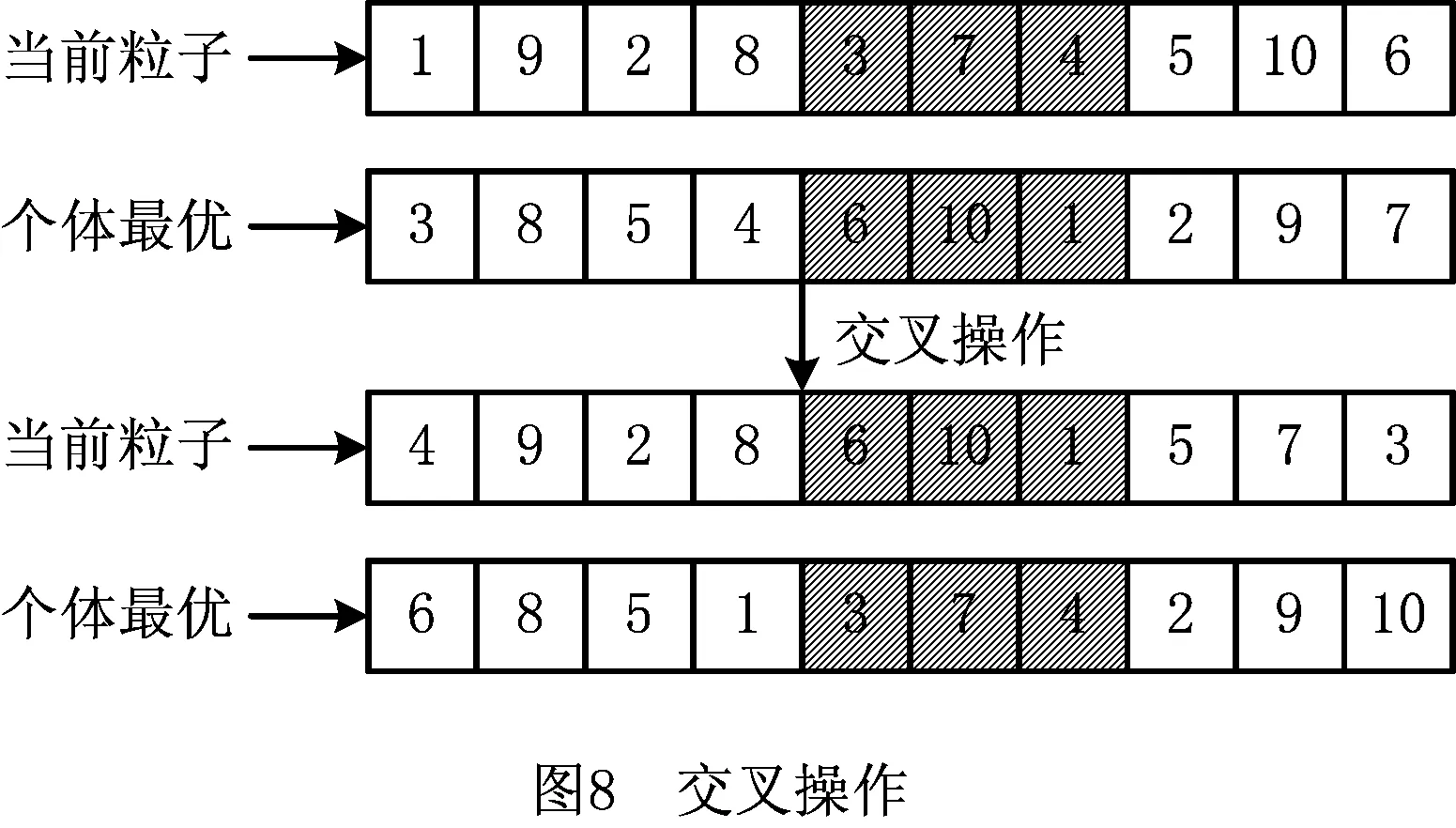
3 实验及结果分析

4 结束语
