基于加权秩和比法的桥梁施工方案优选研究

刘晓佳，张 可

(1.集美大学 航海学院，福建 厦门 361021； 2. 集美大学 海上交通安全研究所，福建 厦门 361021)

0 引 言

桥梁施工方案选择是大桥建设中非常重要的一个环节。如果选择得当既能顺利实现桥梁建设又可以降低综合成本。因此基于可行性和安全性问题从所有备选方案中选择一个综合性强的桥梁施工建设方案是必要的。桥梁施工方案选择需要考虑诸多因素[1]，包括施工费用、安全性、技术方案先进性等。常见的桥梁施工方案选择方法有层次分析法、灰色关联分析法等。但是在桥梁施工过程存在复杂性及决策者的主观性，造成施工方案优选并没有一个统一的方法，一般都是根据具体专家及设计者选择适用的方案[2]。黄玉刚[3]把层次分析法应用到实际工程的施工技术方案比选中，取得了一定的效果；肖安斌[4]提出一种基于格序理论的模糊多目标决策的施工方案优选方法，并验证了该模型方法的可行性；孙吉书等[5]针对影响桥型方案选择的多因素与灰色特征，提出了基于灰色关联分析法的桥型多方案选择方法。但是这些方法在桥梁施工方案选择上存在太过繁琐或者主观性太强的缺点。付学谦等[6]针对现有电能质量综合评估方法模型复杂的问题，提出了基于加权秩和比的电能质量综合评估方法。秩和比法被广泛应用到医疗卫生领域的质量综合评估及方案选择中[7]，在桥梁施工方案选择领域还未涉及到。加权秩和比法具有计算过程简单、无量纲要求、综合能力强的优点。基于此，笔者为了克服在评价过程中人为因素的影响和方案评选过程过于复杂繁琐的问题，利用云理论实现定性指标定量化的转化，提出利用加权秩和比模型对桥梁施工方案进行综合筛选。采用熵权法确定方案指标因素的权重，能够有效避免人为主观性问题。因此采用加权秩和比方法对桥梁施工方案进行优选，不仅能够简化桥梁施工方案的筛选还能够提高筛选的客观性。

1 加权秩和比

1.1 基本原理

秩和比法(RSR)[8]是我国统计学家田凤调教授提出的，应用至今已有30多年历史。该方法被广泛应用于医疗卫生领域的多指标综合评估、统计预测预报等方面。RSR评价法的基本原理是：首先把矩阵秩转化为无量纲统计量RSR，然后运用数学方法研究RSR分布，最后根据RSR值分布对研究对象进行排序及分档[9]。RSR评估方法具有以下4个优点：①计算过程简单；②不受异常值影响；③RSR值无量纲要求；④该方法与数理统计等方法融合较强。

1.2 桥梁施工方案优选步骤

1)确定方案指标值。根据调查得到定量指标，定性指标在专家打分基础上应用云理论进行处理转化为定量指标，具体见第2节“云理论实现定性指标定量化”。

2)构建评价矩阵。假设备选方案有n个，每个方案有m个指标，方案对于各个指标的评价集合记为：aij(i=1,2,,n;j=1,2,,m)，aij构成矩阵A。

3)编秩。根据桥梁方案指标对评价结果的影响确定各个指标是效益型还是成本型指标。对于效益型指标按照从小到大进行编秩即1,2,,n顺序编秩，如果遇到量值相同的两个方案时，则取均值作为其秩。而成本型编秩顺序与之相反。利用该方法得到方案集的秩矩阵Rij。

4)计算指标权重。由于熵值法具有精度高，能有效避免人为主观性的优点，故本文采用熵值法确定指标权重。具体见第3节。

5)求取方案的秩和比。秩和比记为RSR，其值由式(1)计算而得：

(1)

对于考虑加权的秩和比法，其最终的判断依据应该是基于加权的秩和比值，其计算式如式(2):

(2)

式中：ωj为指标的权重值。

probiti=u(pi)+5

(3)

式中：u(pi)为标准正态下的离差函数；pi与probiti可查表得出。

7)计算回归方程。以概率单位probiti为自变量， 以通过回归计算的加权秩和比估计值δWRSRfit作为因变量，计算回归方程：

δWRSRfit=a+bprobiti

(4)

式中：a，b为系数。

8)计算回归后的加权秩和比值并进行分档。参考文献[8]，其分档等级见表1。

表1 分档数及临界值标准Table 1 Numbers of classification and the critical value

2 云理论实现定性指标定量化

在云模型基础上实现的定性指标定量化，具有确定过程简便、专家评价结果直观性强的优点。该方法将专家对指标认识的模糊性和随机性充分考虑进来，能够将多位专家的认识综合考量。因此，采用云理论的方法对定性指标进行处理：首先由专家对各个指标重要性进行打分，然后用云模型里的逆向云和正向云发生器进行处理，得到各个评价指标的云模型，最后对指标重要性云模型期望处理得到评价指标重要性的分值。具体步骤如下：

1)选取行业内的n位资深专家进行评分；假设需要打分的指标有m个记作Ui，用集合表示为{Ui1,Ui2,,Uim}。

2)假设n位专家对评价指标Uij(j=1,2,,m)的评分记为{V1,V2,,Vn}，效益型指标评分值从差到优为0—1，成本型指标评分值从优到差为0—1。经逆向云发生器处理后生成评价指标Uij的重要性数字特征为(Exij,Enij,Heij)。

3)运用正向云发生器生成评价指标重要性分值Uij的云图。

4)观察步骤3)所得云图中云滴的凝聚情况，若云滴呈雾状分布，则认为云滴的凝聚性较差，n位专家评价意见不一致，则需对专家组意见进行积极反馈及有效沟通。如此反复多轮，直到得到能够反映专家组意见统一的、凝聚性好的云图，即评价指标Uij的重要性云模型。

5)多次重复2)～4)步骤，获得所有评价指标的重要性云模型m个。将得到的m个评价指标重要性云模型的期望值作为评价指标重要性Uij的最终云值。

2.1 正向云发生器

输入：反映指标重要性定性概念的数字特征(Ex,En,He)以及生成的云滴个数N；输出：N个云滴xi和每个云滴对概念的隶属度。正向云发生器的具体算法如下：

2)生成以Ex为期望值，En′为标准差的正态随机数xi。

3)计算xi的隶属度：

(5)

4)重复1)～3)直至产生N个云滴。

2.2 逆向云发生器

逆向云发生器的作用是从一些给定的云滴中，求出正向云发生器的3个数字特征值(Ex,En,He)。

改进的逆向云发生器的算法实现更为简单，且不需确定度信息，因此更适合确定度未知的情况。改进的逆向云发生器的具体算法如下：

1)输入：将专家给出的指标重要性分值作为样本值x=xi，其中i=1,2,,n。

2)输出：反应指标重要性定性概念的数字特征(Ex,En,He)通过xi计算样本均值：

(6)

(7)

(8)

3 指标权重确定方法

熵值法是一种客观赋权的方法。其基本原理是在求得指标权重过程中根据各个指标的变异程度，利用信息熵计算得出各个指标的熵权，然后根据熵权对各个指标的权重进行修正，最终得到较为客观的指标权重值。

设评估矩阵为A=(aij)n×m，指标权重计算步骤如下[10]：

1)采用标准0—1变换将各项指标进行标准化处理。当指标为效益型时，标准化公式为：

(9)

式中：i=1,2,,n；j=1,2,,m。(下同)

当指标为成本型时，标准化公式为：

(10)

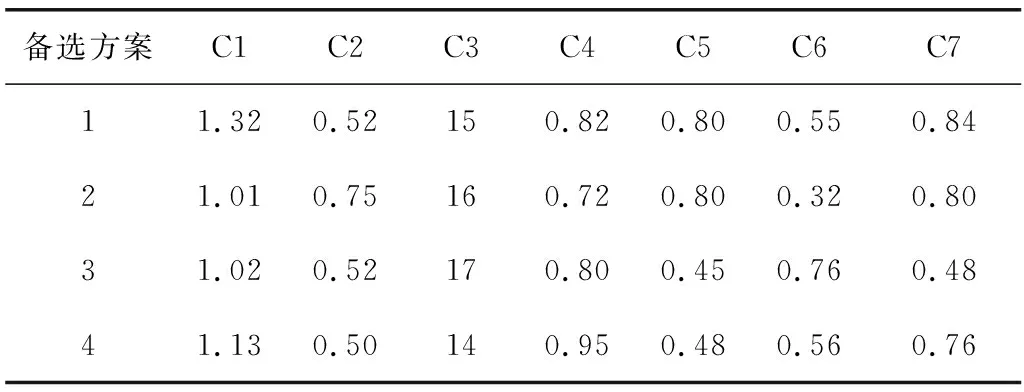
2)依据标准化决策矩阵，求第j个指标第i个评估样本的特征比重，其中0

(11)

3)第j个指标的熵值为：

(12)

对于特殊情况，当pij=0，取lnpij=0。

4)第j个指标的差异系数为：

gj=1-ej

(13)

5)第j个指标的熵权重为：

(14)

4 算例分析

某市拟建设一条大桥，现有4个备选方案。笔者在查阅大量文献及咨询专家的基础上优选出7项具有代表意义的指标，分别是施工费用C1(单位：亿)、施工安全性C2、施工周期C3(单位：月)、施工难易程度C4、技术方案先进性C5、对环境影响C6、对经济的促进作用C7。

在评价指标中考虑到定性指标太多，对其重要性确定时需进行一系列处理方能得到最终数据。运用上文云理论的方法对各个定性指标进行处理。

采用云模型对评价指标重要性进行确定，以表2中方案1中指标“施工安全性”为例，对打分情况作具体介绍。由10位专家及桥梁施工资深工作者组成专家组，对方案指标重要性进行打分。收集由10位人员组成的专家组对“施工安全性”首轮打分的结果(0.7,0.5,0.2,0.5,0.6,0.4,0.9,0.7,0.6,0.6)，经过逆向云发生器得数字特征(0.57,0.170 5,0.081 3)，采用正向云发生器得出云图，见图1(a)。可见云滴的离散程度较大，云图整体呈现雾状，这表明专家意见不统一。需要将专家组打分情况反馈给专家组，让其再次打分，经过多次重复直至得到比较集中的正态云图，最终得到数字特征为(0.52,0.083,0.01)的云图，如图1(b)，则表明专家组意见基本一致。最终确定方案1中“施工安全性”指标重要性分值为0.52。同样方法得到各个方案定性指标重要性分值，得到所有方案数据，见表2。

图1 评价指标重要性得分云图Fig. 1 Score cloud map of evaluation index importance

备选方案C1C2C3C4C5C6C711.320.52150.820.800.550.8421.010.75160.720.800.320.8031.020.52170.800.450.760.4841.130.50140.950.480.560.76

利用第3节中介绍的熵值法计算得到的指标权重为：

ω′=(0.1239,0.2065,0.1333,0.1253,0.1581,0.1313,0.1215)

利用1.2节中步骤对方案进行编秩及加权秩和比的结果如表3。

表3 编秩结果和加权秩和比Table 3 Coding rank result and weighted rank sum ration

δWRSRfit=-0.479 86+0.205 08probit

(15)

利用回归方程得到的加权RSR估计值δWRSRfit，如表4，δWRSRfit越大代表方案越优，可信度越高。

表4 加权秩和比分布Table 4 Distribution of weighted rank sum ratio

对由上述方法得到的评估结果进行由大到小排序，排序结果为方案2、方案1、方案4、方案3，则最优为方案2。参考表1按照4个等级进行划分，通过处理计算得到的分类结果，如表5。由表5可知方案2为优质等级，方案1为良好等级，则最终采用方案2，与该市最终采用的桥梁施工方案对比，发现结果一致。

表5 评价结果排序Table 5 Ranking of evaluation results

5 结 语

采用加权秩和比法对桥梁施工方案进行优选，提出了一种桥梁施工方案优选的新方法，构建了基于熵值法的加权秩和比模型。首先在构建指标体系后用云理论实现定性指标定量化转化得到施工方案数据，然后在得到指标权重基础上确定各个施工方案的加权秩和比和概率单位，并利用MATLAB软件计算得到回归方程，最后根据加权秩和比值选出最优方案。熵值法在确定权重时避免了多因素权重确定的主观性。构建的模型不仅能够较好的处理定性指标定量化间的转化而且能够快速可靠的选出最优方案，同时也为桥梁施工方案选择提供了新方法。