轻量化起升机构的两支点减速器支撑多目标优化设计

朱慧云，王淑妍+，吕渌渊，陈 星，丁 进

(1.江苏科技大学 机械工程学院，江苏 镇江 212003；2.江苏科技大学 江苏省船海机械装备先进制造重点实验室，江苏 镇江 212003)

0 引言

作为桥式起重机的关键组成部件，起升机构能否高效运行直接关系到整机的安全运行和经济效益。减速器为起升机构的核心驱动组件，其力学性能直接影响整机的运行。轻量化起升机构的布局和支撑位置直接影响减速器的动静态特性，在既有布局下如何合理优化支撑位置减轻减速器的变形和振动，对整机正常运行具有重要的意义[1]。

国内外学者针对起升机构的轻量化开展了相关研究。贾旺兴等[2]在优化小车零部件的基础上，优化了起升机构的布置形式，从而减轻了小车架的自重；张玉等[3]提出一种新型的起升机构布置形式，减小了小车架的刚性，降低了小车重量和整机高度；张东海等[4]分析了新型布局的轻量化起升机构的动力学特性和整机的受力状况，提出新型布局设计的重要环节及薄弱点；钟明等[5]分析了传统起升机构中减速器在不同工况下的力学特性，并提出设计中的薄弱点以及相应的改进方案。

在工程结构、形状优化中，常采用响应面法构建优化中某些函数的近似表达。响应面法最初由Box等[6]于1951年提出，主要应用于化工领域，1959年Box等[7]将这种方法定义为“在经验模型构造和开发中应用的一组统计学技术”。唐乃梅等[8]基于响应面法对膜结构进行截面优化；任旭春等[9]给出一种序列局部响应面的自适应方案，以求解轮胎胎冠形状优化问题；隋允康等[10-11]将中心点精确响应面法运用到二维连续体形状优化中，并基于中心复合和单纯形试验设计方法将其引入桁架截面优化中。此外，张兵等[12]采用有限元方法对板簧压板进行多目标优化设计，最终得到其轻量化模型；段明德等[13]采用灵敏度分析方法，研究了多个床鞍结构参数对床鞍多种动态特性的影响规律，并求得最优解。

本文以32 t轻量化桥式起重机三点支撑的起升机构为研究对象，通过建立起升机构的整体力学分析模型，开展该布局下仅有两点支撑的减速器静力学分析，并采用响应面与多目标优化结合的设计方法研究减速器的变形和受力状况。

1 基于响应面方法的结构优化设计

传统的结构优化设计是由设计者提供几个不同的设计方案，从中比较、挑选出最优方案。但是这种优化方法往往建立在设计者经验的基础上，而时间与资源均有限，提供的可选方案数量也有限，所挑选的不一定是最优方案。要想获得最优方案，就要提供更多的设计方案进行比较，由此需要大量的资源，单靠人力难以做到，只能依靠计算机完成优化。目前，ANSYS软件拥有强大的优化设计功能，可以实现结构尺寸优化，且其本身提供的算法也能满足工程需要。ANSYS Workbench环境(ANSYS Workbench Environment，AWE)是ANSYS公司开发的新一代前后处理环境，提供了与CAD软件及设计流程高度的集成性。CAD模型需改进的设计变量可以传递到AWE环境下,并且其中的DesignXplorer模块设定约束条件及设计目标后，可以高度自动化地实现优化设计并生成相关图表。

本文采用Pro/E和ANSYS软件在AWE环境下实现起升机构的快速优化设计，优化设计流程如图1所示。

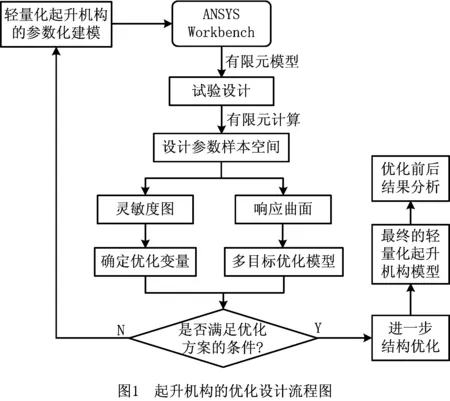
2 轻量化起升机构的集成布局分析

轻量化桥式起重机起升机构采用整体三支点的集成布局形式，如图2所示。其中，电机、减速器均采用无底座安装形式。电机通过法兰套筒刚性连接在减速器箱体上；减速器的花键输出轴通过刚性锥形接手与卷筒法兰板连接；卷筒通过卷筒轴承座和减速器简支座，半卧式布置在底部的小车架两端的端梁上。

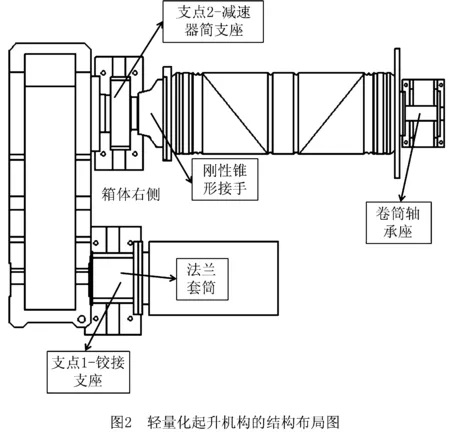
在轻量化起升机构中，减速器只有两个支撑点，悬臂支撑在轴承座和简支座上，这和传统的支撑方式存在很大差别，其力学性能也不能按照常规方法分析。因此，基于起升机构整机力学分析，综合考虑组件的自重及分布、卷筒提升重物的自重、支撑座的支撑位置、满载时电机的输入功率等影响其力学性能的因素，建立轻量化起升机构起升工况时的受力分布简图，如图3所示。

图中：F1为减速器输入端支撑件(铰接支座)的支反力;F2和F3分别为减速器输出端支撑件(减速器简支座)在Z向和Y向的支反力;F4,F5和F6分别为卷筒轴承座在Z向、X向和Y向的支反力;Gm表示电机的自重;Tm为电机的输入转矩;xm为电机的质心距离减速器右侧的距离;ym为电机的质心距离卷筒轴的距离;x1为铰接支座质心距减速器右侧的距离，初始值为20 mm;y1为铰接支座质心距离卷筒轴的距离;Gr为减速器的自重，B为减速器箱壁距离;xr为减速器质心距离减速器右侧的距离;yr为减速器质心距离卷筒轴的距离;x2为减速器简支座质心距离减速器右侧的距离，初始值为90 mm;Fmax为提升重物时施加在钢丝绳上的集中力;M为集中力Fmax产生的弯矩;D为卷筒直径;Gd为卷筒系统自重;Ls为减速器简支座质心距离最近的集中力Fmax的距离;xd为两处集中力Fmax之间的距离;L为减速器简支座质心与卷筒轴承座质心的距离;L1为减速器右侧距卷筒轴承座的距离。

起升工况中，整机的空间力系仍处于平衡状态，整个起升机构的主矢和对于任一点的主矩均等于零。由此可计算出起升机构3个支撑座处的支反力F1,F2,F3,F4,F5和F6:

F3=F5=F6=0;

(1)

F1=S0/y1-Gm;

(2)

Gmxm+Fmax·S1+Gr·S2+Gd·S3];

(3)

F4=S0/y1+Gd+Gr+2Fmax-F2。

(4)

式中：S0=Fmax·D-Gr·yr，S1=LD/y1+2L-2Ls-xd，S2=L+xr-yr·L/y1,S3=L-Ls-0.5xd,x1∈[0,xm],x2∈[0,L1-L]。

2.1 两支点支撑减速器的输入端

在两支点支撑的减速器中，电机悬臂支撑在减速器箱体上,不可避免会增加减速器输入端的变形。根据图3载荷分布图，将减速器的输入轴端简化为外伸梁结构，如图4所示。

同时，利用材料力学中的逐段刚化法[14]，计算输入轴末端的总变形量d：

(5)

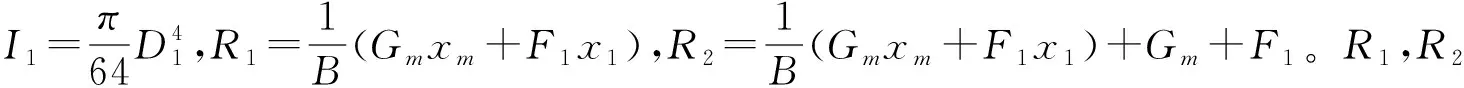
由式(5)可知，在其他因素不变时，输入轴末端的总变形量d与设计变量x1呈正相关关系。

2.2 两支点支撑减速器的输出端

两支点支撑减速器中输出端承担载荷较大，因此减速器应力值最大处位于输出轴末端，最大弯曲应力值为

Gmxm+Fmax·S1+Gr·S2+Gd·S3}。

(6)

由式(6)可知，输出轴端的应力与变量x1和x2均相关：

(1)在其他因素不变时，减速器输出端的弯曲应力σ与设计变量x1呈反相关关系。

(2)在其他因素不变时，减速器输出端的弯曲应力σ与设计变量x2呈正相关关系。

2.3 试验验证

在理论分析的基础上，对轻量化起升机构的两支点减速器进行不同工况下不同测点的应力应变试验，如图5所示。

通过试验得出结论：轻量化桥式起重机起升机构中，在额定转速为1 500 r/min时，减速器各测点最大主应力为78.76 MPa，出现在正转输入1 500 r/min，41.90 kN·m工况下减速器的输出端。该试验结果和理论模型一致，减速器应力值最大处位于输出轴末端。

2.4 结果分析

通过对起升机构的基础力学分析，可得：

(1)在两支点支撑的减速器中，输入轴末端的变形量最大；此外，输入轴末端变形量d与铰接支座质心距减速器右侧的距离x1呈正相关关系。

(2)在两支点支撑的减速器中，输出轴末端的减速器的弯曲应力值最大；此外，输出轴末端应力值σ与铰接支座质心距减速器右侧的距离x1呈反相关关系，与减速器简支座质心距离减速器右侧的距离x2呈正相关关系。

3 减速器支撑位置的优化设计

3.1 参数化有限元模型的建立

以QY型桥式起重机起升机构为例，设工作级别为M5,传动比为124，卷筒直径为500 mm，起重量32 t，通过Pro/E建立轻量化起升机构模型，并利用专用接口将其导入ANSYS Workbench软件，分别设置模型的材料属性，如表1所示；同时，对轻量化起升机构划分网格，如图5所示。

表1 起升机构组件的材料属性 MPa

对轻量化起升机构施加载荷和约束，利用有限元方法进行整体的力学特性分析计算，得出两支点支撑的减速器变形云图和应力云图，分别如图6和图7所示。其中，减速器的最大变形位于输入轴末端，最大应力位于输出轴末端，与理论分析的结果一致。此外，减速器的最大变形量为0.203 mm，最大应力值为327.91 MPa(x1=20 mm，x2=90 mm)，根据机械设计手册以及表1的材料属性，最大变形和最大应力值均在许可范围内。但是，为使减速器的力学特性最优，还需针对最大应力值和最大变形量进行优化。

3.2 减速器支撑位置的多目标优化设计

(1)确定优化目标

将降低减速器的最大应力值σ和最大变形量d设为优化目标，采用响应面方法对减速器的支撑位置进行多目标优化设计。

(2)确定设计变量

在两支点支撑的减速器中，虽然影响减速器最大应力和应变的因素较多，但是本文减速器的型号、工作级别和配套零部件已固定，只有减速器两侧的支撑位置对应力和应变有影响。故可变因子设置为铰接支座质心距减速器右侧的距离x1和减速器简支座质心距离减速器右侧的距离x2。

即设计变量

X=[x1,x2]T。

(7)

式中：x1∈[0,100]，x2∈[0,90]，x1和x2均沿远离减速器的方向移动。

(3)确定约束条件

减速器是起升机构的重要传动部件，在对减速器的力学特性进行优化时，会改变减速器应力，因此为了保证整机的优化效果，需保证箱体中的最大应力处输出轴的应力在许用强度范围内，根据表1中的材料属性，约束条件为

σ-(1 180/k)≤0。

(8)

式中k表示安全系数，一般k=1.5。

(4)确定目标函数

综合考虑减速器优化的工程经验，选取具有较高准确性的二阶响应面模型，设计变量为X，响应面模型表示如下：

f1(X)=α0+α1X+α11X2;

(9)

f2(X)=β0+β1X+β11X2。

(10)

其中:式(9)和式(10)分别表示减速器的最大变形量f1(X)和最大应力值f2(X)与设计变量X的变化函数;α0,β0为常数项待定系数;α1,β1为一次项待定系数;α11,β11为二次项待定系数。

3.3 灵敏度及响应面分析

(1)试验设计

完成静力学分析后，将减速器的最大变形量和最大应力值设置为输出参数，进行实验设计(Design of Experiment，DOE)，在DOE表格中输入设计变量的变化范围，进行设计样本点采集。本文有两个优化参数，生成17个数据样本点，如表2所示。

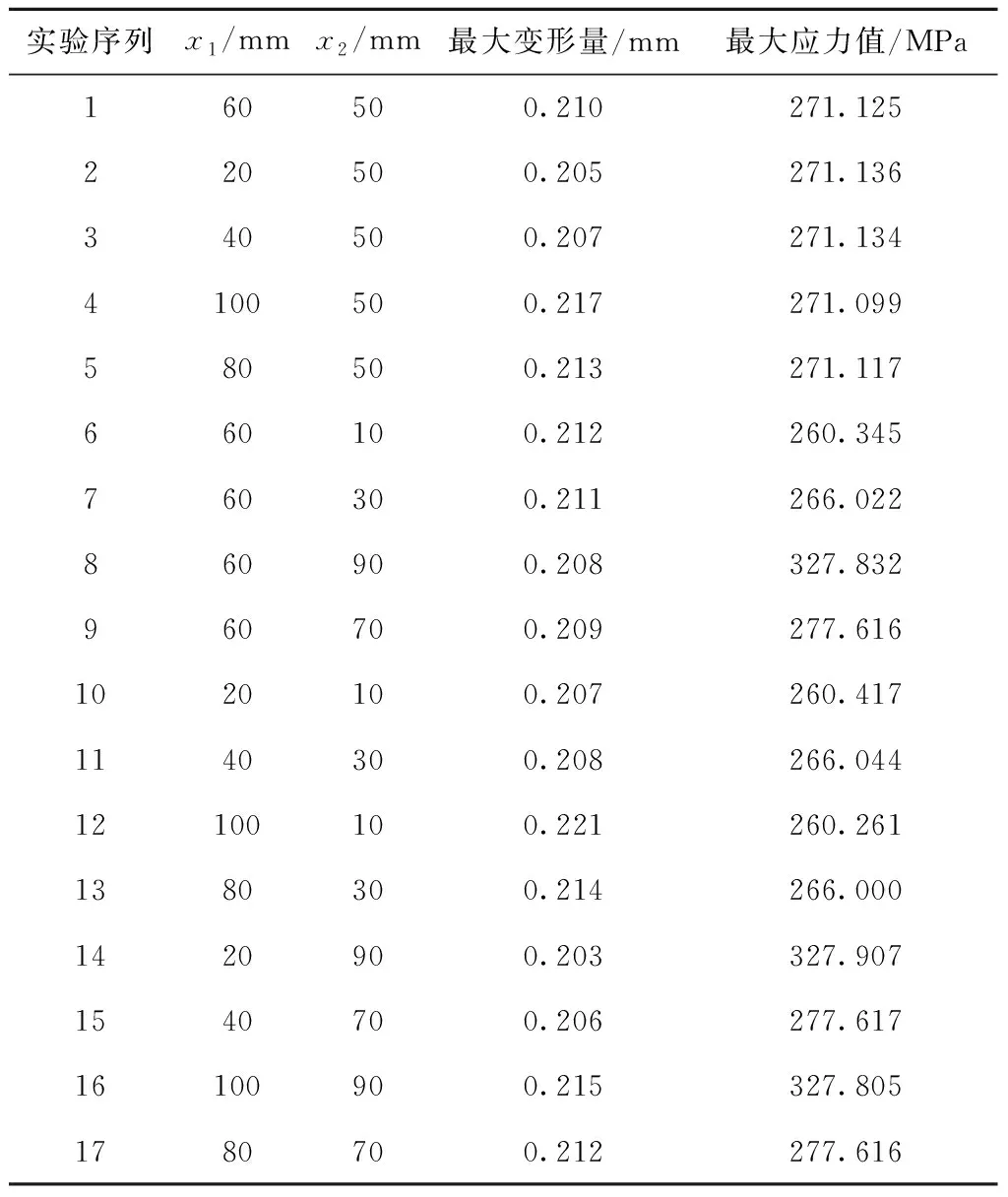
表2 DOE数据样本点

(2)灵敏度分析

结构灵敏度分析计算反映设计变量对性能指标的影响程度，以及设计变量与性能指标的变化趋势，如图8所示。

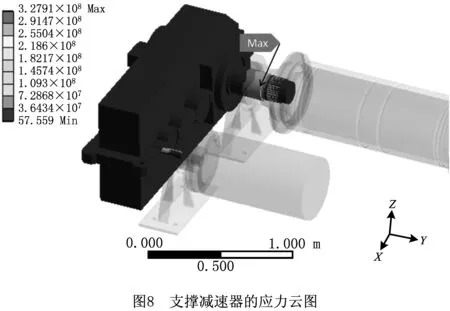
设计变量x1和x2对最大变形量f1(X)和最大应力值f2(X)的变化趋势如图9和图10所示。

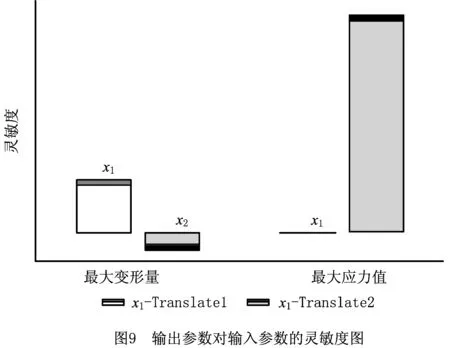
由上述变化趋势图可得：

1)设计变量x1对减速器最大变形量f1(X)的影响较大，且呈正相关(如图9a)；而设计变量x2对变形的影响较小，但呈反相关(如图9b)。

2)设计变量x1对减速器最大应力f2(X)呈反相关(如图10a)，但影响很小，可忽略不计；而设计变量x2对最大应力的影响很大，且呈正相关关系(如图10b)。

(3)响应面分析

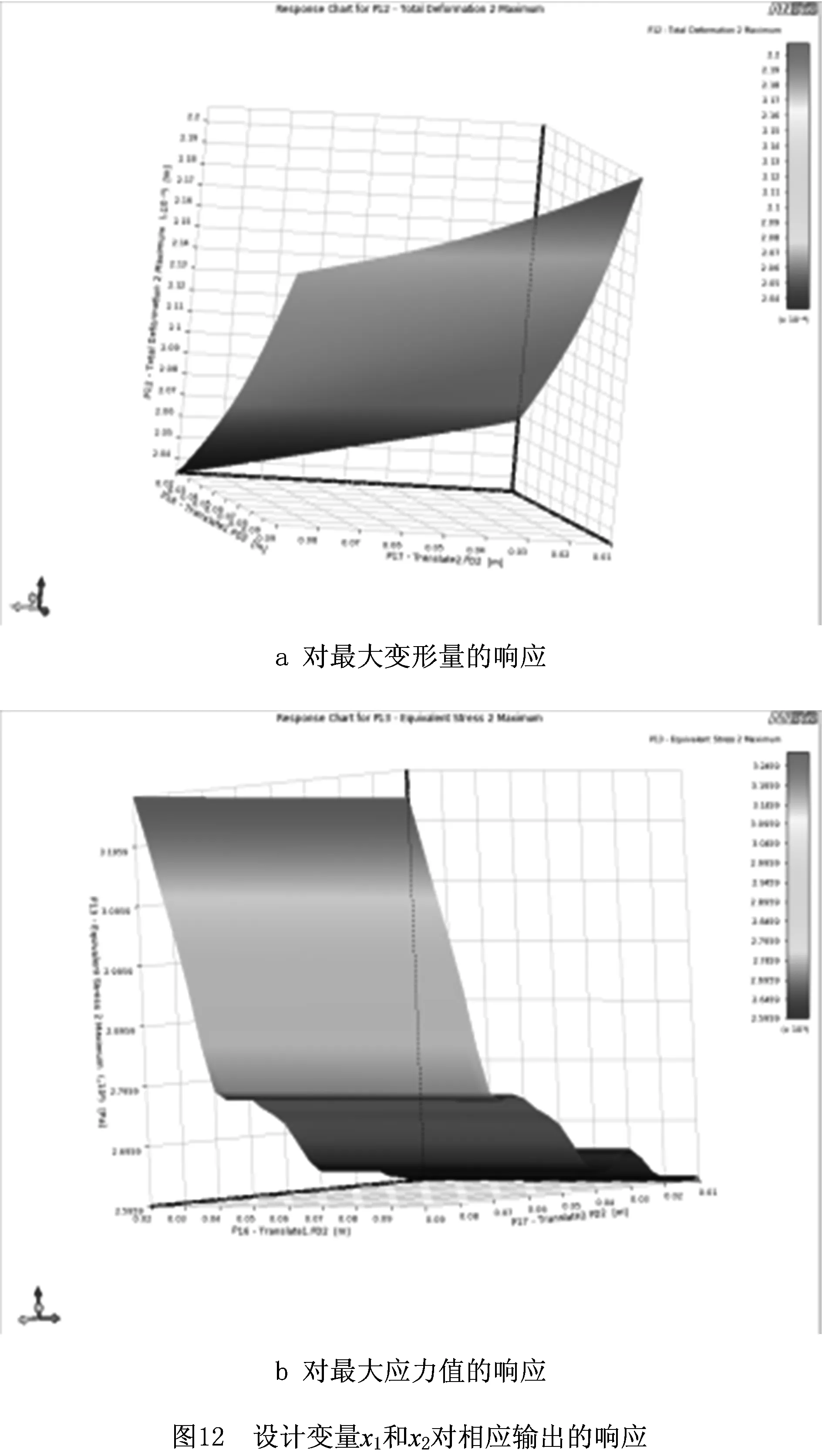
设计变量x1和x2对减速器的最大变形量f1(X)、最大应力值f2(X)的输出响应如图11所示。其中，坐标系中每个点分别对应一个x1，x2和一个相应的响应数值。

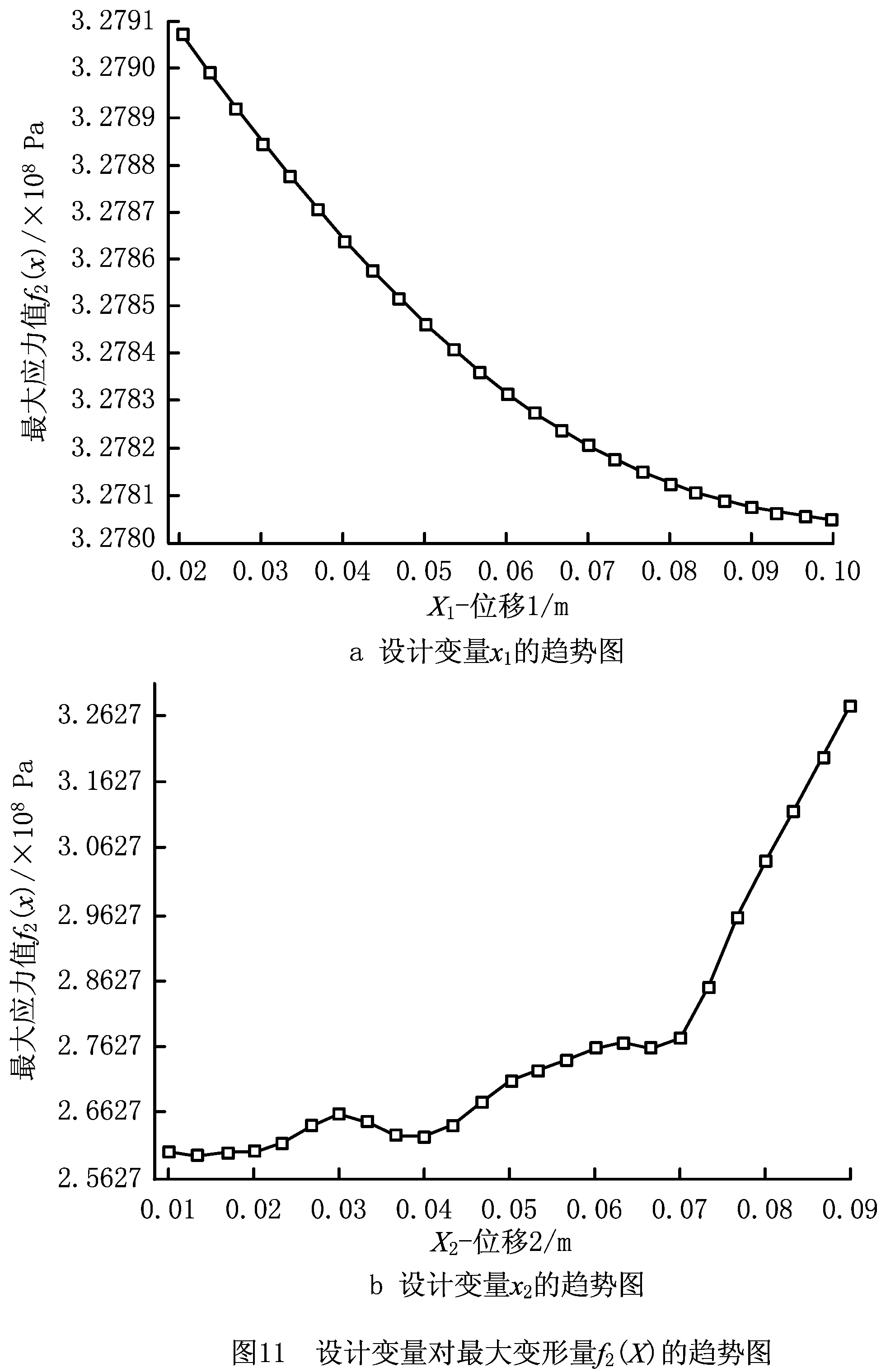
3.4 优化结果分析

设定优化目标，求解减速器的最大变形量和最大应力值的最小值，对样本参数综合分析求解，得到最大变形量f1(X)和最大应力值f2(X)最优的3组参数组合方案，如表3所示。

表3 最优参数组合方案

根据优化结果可得，要使f1(X)和f2(X)均取得最小值，综合考虑设计变量x1和x2对二者的影响，选取第1组方案为减速器支撑位置的最优值。圆整后设计变量的值为x1=20 mm,x2=40 mm。

4 减速器支撑位置的进一步优化

根据设计变量x1和x2与力学性能的相关性，对整体结构进行进一步优化，优化前后轻量化起升机构的结构简图分别如图12a和图12b所示。其中，输入端处铰接支座支撑点设置在减速器箱体上，设计变量x1减小至零；同时，输出端处支撑座支点的设计变量x2取最优值40 mm。

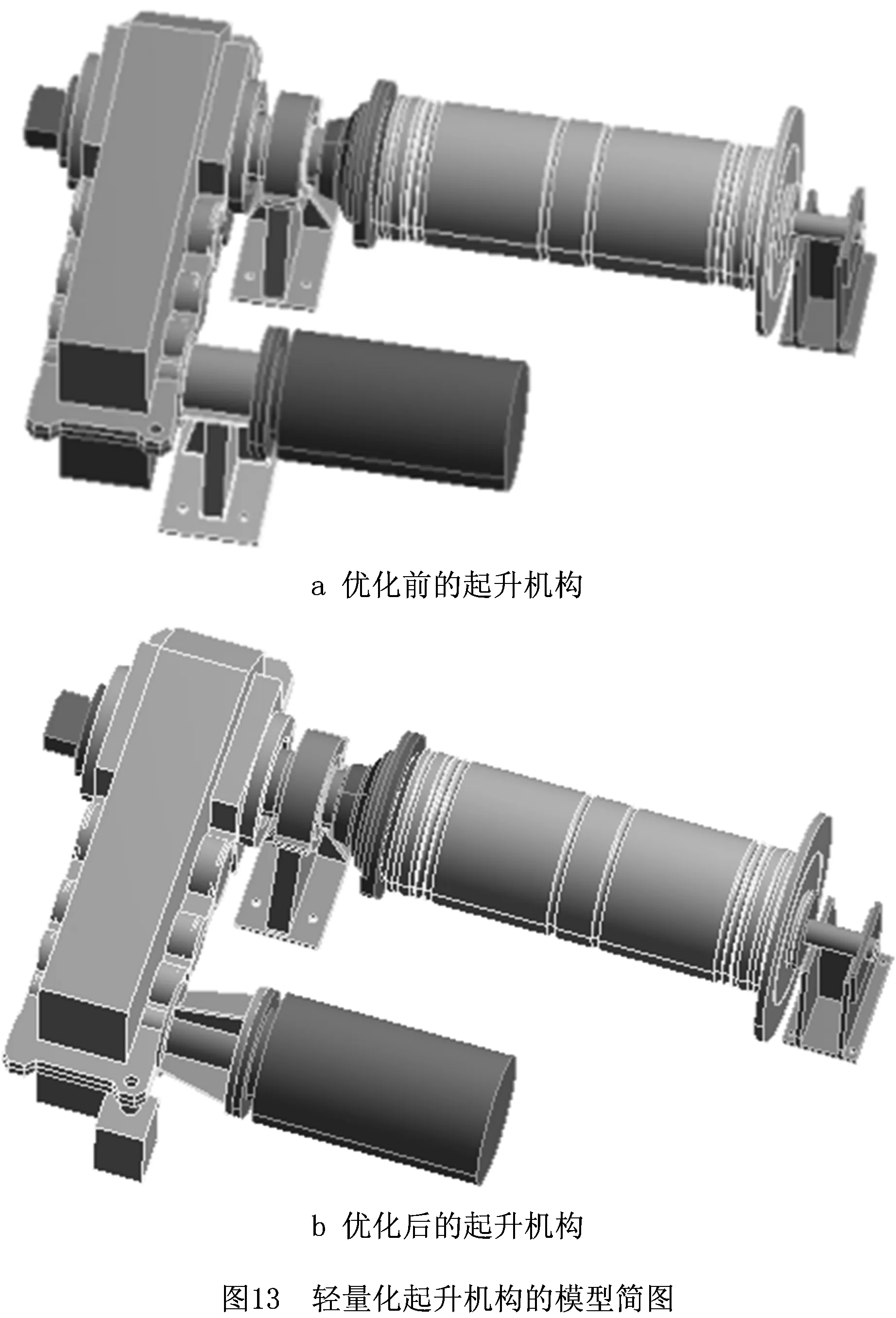
对优化后起升机构中的减速器进行有限元计算，得到减速器优化前后的性能对比，其模型简图如图13所示，各参数对比如表4所示。其中，优化后减速器的最大变形量降低16.3%，最大应力值降低23.8%。在满足起升机构力学性能的前提下，对减速器两侧支撑件的位置进行优化，降低了减速器的最大变形和最大应力，得到最优的减速器支撑位置。

表4 优化前后减速器力学性能比较

5 结束语

本文采用基础力学分析和有限元分析方法，建立了轻量化起升机构起升工况的参数化有限元模型，研究了箱体两支点支撑位置对减速器力学性能的影响，并结合响应面优化方法和多目标优方法对支撑点位置进行了优化，得出以下结论：

(1)运用基础力学对两支点支撑的减速器开展力学特性分析计算，得出减速器的最大变形和最大应力位置分别位于输入轴末端和输出轴末端。同时，输入轴端的最大变形量与输入端支撑件的设计变量x1呈正相关关系；输出轴末端的最大应力值与输入端支撑件的设计变量x1呈反相关关系，与输出端支撑件的设计变量x2呈正相关关系。

(2)利用ANSYS workbench计算出减速器的整体力学特性，同时通过响应面方法分析两支点支撑位置对整体力学特性的影响，以验证基础力学分析的结果，并结合多目标优化方法得出减速器支撑位置的优化方案。

(3)依据优化结果对起升机构的整体结构进行进一步优化，得到两支点支撑的减速器最优支撑位置。研究结果表明，优化后减速器的力学性能明显提高，与原结构相比，最大变形量降低了16.3%，最大应力值降低了23.8%。

综上所述，通过对减速器的力学特性分析，结合优化设计方法和实验验证，完成了轻量化起升机构的整体结构优化，后续结合动力学特性分析，研究不同的运行工况对轻量化起升机构的整体力学特性的影响。