复杂生产系统经济生产批量与视情维护策略模型
2018-10-18成国庆周炳海
成国庆,周炳海,李 玲
(1.同济大学 机械与能源工程学院, 上海 201804;2.上海海洋大学 工程学院, 上海 201306;3.上海立信会计金融学院 统计与数学学院,上海 201209)
0 引言
生产设备的日益复杂化、集成化和智能化直接加大了设备维护和保养的难度,维护费用和强度不断增高,从而对维护决策与优化提出了更高的要求。据统计,设备的维修、维护费用大约占总生产成本的15%~70%[1]。因此,如何妥善维护这些复杂的生产设备、保障其高效运行、降低生产维护总成本是企业在提升竞争力方面遇到的一项实际课题,也是“中国制造2025”发展战略关注的焦点之一。
自上世纪90年代以来,有很多学者对设备的生产与维护联合优化问题进行了深入而广泛的研究。早期的生产维护联合优化模型在维护方式上基本都采用基于役龄的预防维护策略[2-4],这难免会导致“维护过剩”或“维护不足”。随着传感、设备诊断、故障预测等技术的发展,维护活动可根据设备实时或接近实时运行状态的诊断、评估结果来选择相应的预防性维护措施[5]。基于设备运行状态的维护(即视情维护)策略比基于役龄的维护策略更高效,因此其在工程中的应用越来越广泛。文献[6]以马尔科夫过程刻画设备的劣化进程,研究了生产批量与视情维护策略的联合优化模型,并利用半马尔科夫决策方法进行了求解。文献[7]利用更新过程理论建立了生产批量与视情维护策略的联合优化模型。文献[8]进一步考虑了生产过程会出现次品的情形,并假设次品率与设备的劣化状态相关。
以上文献在研究生产设备时均将其视为一个独立的个体,即看作是一个单部件系统。然而,由于生产设备日益复杂化和集成化,部件数目迅速增长且部件之间的劣化故障机理相差甚大,在制定维护策略时很难将其视为一个简单的个体。对于多部件系统而言,部件之间可能还存在着随机相关性、经济相关性和结构相关性[9],这无疑增加了维护优化的难度。有较多学者对随机相关性问题与经济相关性问题进行了研究。相比之下,结构相关性方面的研究很少,而同时考虑视情维护的研究就更少了。当考虑结构相关性时,挑选部件进行维护不仅要依据其当前状态或可靠性,还要依据其在整个系统中的地位(即结构重要程度)。为此,Birnbaum[10]首先提出了部件的结构重要度概念,随后,其被应用于复杂系统的维护建模问题[11-12]。
目前针对复杂系统的研究仅考虑了单纯的维护问题,未将其置于实际生产环境中。事实上,生产活动对维护策略的制定具有重要的影响。维护活动固然可提高系统可靠性、减少随机故障,但频繁维护会导致产能下降,增加缺货损失风险,故在制定维护策略时必须考虑产能与需求间的矛盾。又如,为尽量保证生产过程的连续性(一些生产活动对连续性要求很高),维护时间节点的选择是受限的,只能是在一个生产批量结束后进行,而这些问题在单纯的维护模型中不会遇到。
鉴于此,本文以复杂多部件生产系统为对象,研究了有限时间域内经济生产批量与视情维护策略的联合优化模型。不仅考虑了部件间的结构相关性,还针对不同部件劣化故障机理的不同,分别利用Weibull分布与Gamma过程对其寿命或劣化过程进行建模。设计了基于蒙特卡洛仿真的优化算法,对总成本进行了优化求解。最后,以集束型晶圆制造设备为例演示了本模型。并通过敏感性分析将本模型与部件独立维护模型、单一整体维护模型进行了实验对比。
1 模型描述
1.1 生产系统描述
考虑一个多部件生产系统,其由N个部件通过串联、并联或串并混联的形式构成。该生产系统在有限的生产期限T内,以生产率P生产某种产品,用于满足需求率为D的外部市场需求(P>D)。
系统中各个部件随着役龄的增长逐渐劣化,当劣化到一定程度时,部件发生故障。在一个复杂的多部件系统中,各部件的劣化、故障机理呈现多样化的特征,难以用单一的寿命分布或随机过程来刻画。例如,在集束型晶圆加工设备内部,氧化工艺腔体采用湿氧氧化进行热生长,腔体受到气体腐蚀,其劣化形式主要体现为腐蚀过程。Gamma过程是递增地、具有独立增量的随机过程,易于进行数学上的解析处理。工程实际中的许多劣化现象如腐蚀、磨损、裂纹增长等都可由Gamma过程很好的进行模拟刻画[13],故本文采用Gamma过程来拟合设备中某些腔体的劣化进程。而另外一些腔体,如化学机械研磨腔体用来对硅片做平坦化处理,可视其为一般的机械部件。Weibull分布是可靠性建模中常用的分布之一,适用于电子元件、机械部件等的寿命刻画。故此处利用Weibull分布来描述某些腔体的随机寿命。将系统中的部件分为两类,其中一类部件i(1≤i≤m)用Weibull分布Fi(t)=1-e-(t/ηi)mi来刻画其寿命;另一类部件j(m+1≤j≤N)用Gamma过程来描述其劣化过程。设部件j在时刻t的劣化量为Xj(t),由Gamma过程的定义[13],Xj(t)是连续时间上的独立增量过程,且Xj(0)=0。设t1至t2时间段内的劣化增量Xj(t2)-Xj(t1)是服从形状参数为αj、尺度参数为βj的Gamma分布,即Xj(t2)-Xj(t1)的概率密度函数为

在一个由多部件组成的系统中,某个部件的故障可能不会导致整个系统的停机,这取决于整个系统的结构以及该部件在系统中所处的位置。如串联结构中某个部件的故障会导致整个系统停机,称这样的部件为“关键部件”;而并联结构中某个部件的故障暂时不会影响整个系统的运行,则称这样的部件为“非关键部件”。如图1所示的串、并混联系统中,部件1为关键部件,其余均为非关键部件。值得注意的是,当部件5故障后,原本非关键的部件6、7则变为关键部件,称它们为“临时关键部件”。当部件6故障后,部件7停止工作,假设停止运行后的部件不再劣化、役龄也不增长。
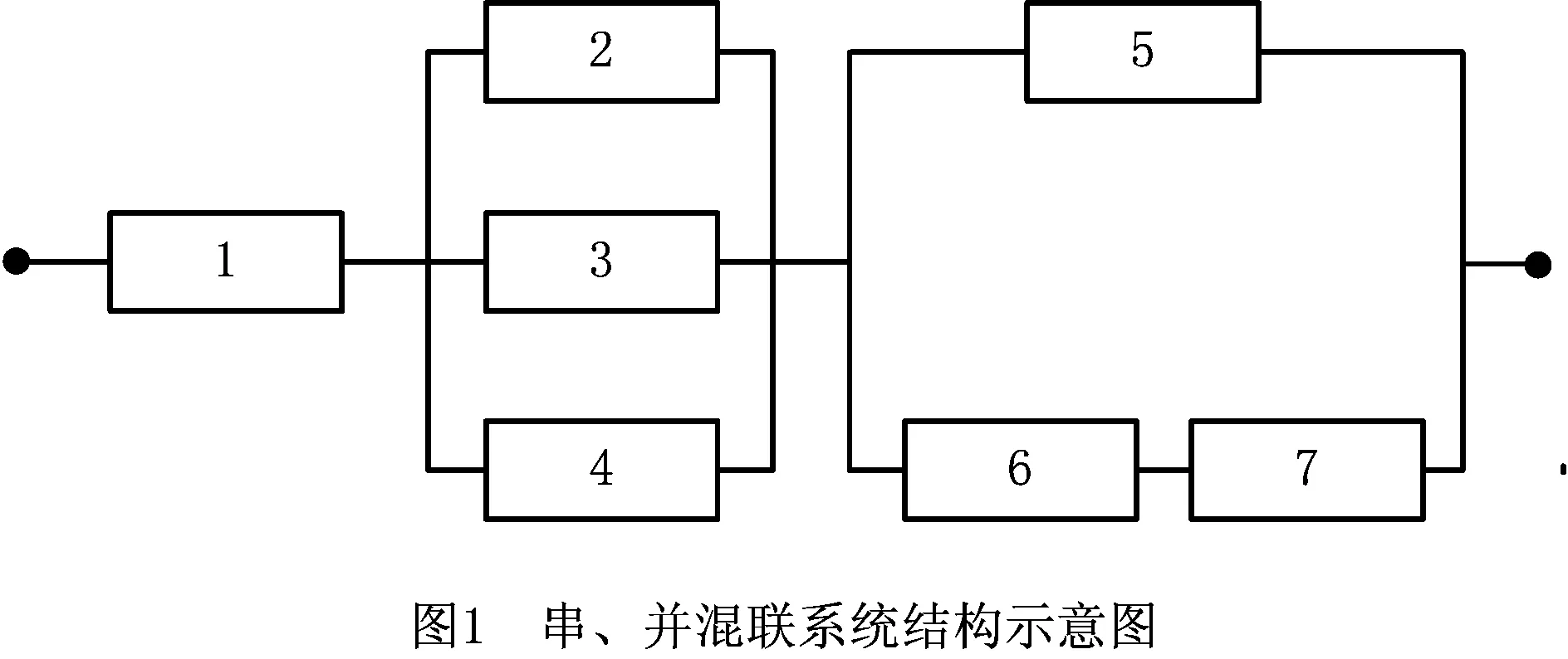
由上述分析可知,不同部件对系统可靠性的影响不一样,改善某些部件的可靠性,对整个系统可靠性的提升效果也不尽相同。因此,在有限的时间和维修资源约束下,如何选择部件进行维护以使系统可靠性得到最大程度的改善,是多部件系统在进行维护决策时面临的一个现实问题。为此,通过Birnbaum结构重要度[10]来刻画单个部件对系统可靠性的影响。设IBi为部件i的结构重要度,y=(y1,…,yi,…,yN)为系统的状态向量,其中yi为二元变量,yi=1表示部件i正常工作、yi=0表示部件i故障。设φ(y)为系统的状态函数,若系统状态正常,则φ(y)=1;若系统故障,则φ(y)=0。当固定部件i的状态为1i或0i时,系统状态(·i,y)=(y1,…,·i,…,yN)有2N-1个不同的值。根据Birnbaum结构重要度的定义[10],IBi为部件i作为关键状态部件在状态总数中所占的比例,
(1)
在图1所示的串—并混联系统中,由式(1)可得IB1=35/64=0.546 9,IB2=IB3=IB4=5/64=0.078 1,IB5=21/64=0.328 1以及IB6=IB7=7/64=0.109 4。
1.2 维护策略描述
1.2.1 预防性维护策略
为改善生产系统的可靠性、减少系统在生产过程中的故障停机损失,在每个生产批量Q结束时,停机对系统中第二种类型的部件(劣化进程由Gamma过程刻画)进行检测。根据部件目前的劣化水平,评估部件在下一个生产批量内的可靠性。令τ=Q/P为一个生产批量的生产时间。假设在第n个批量结束时,检测到部件j(m+1≤j≤N)的劣化水平为Xj(tn)=xj,则部件j在下个批量内的可靠性可表示为
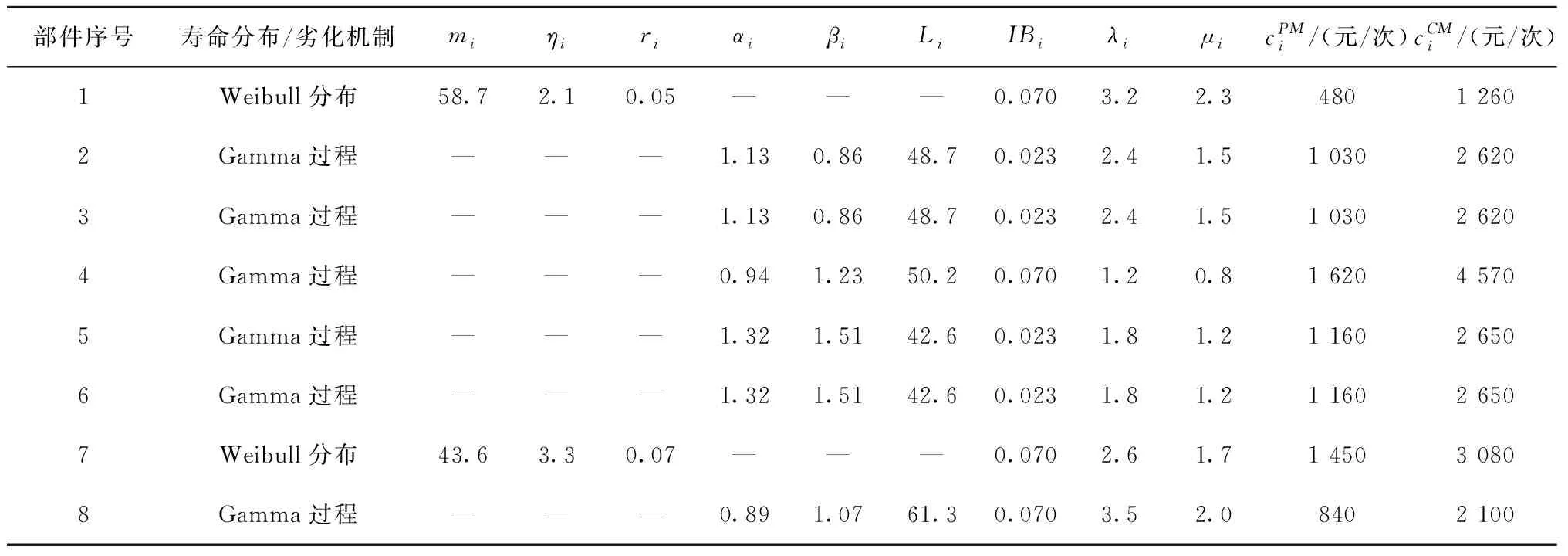
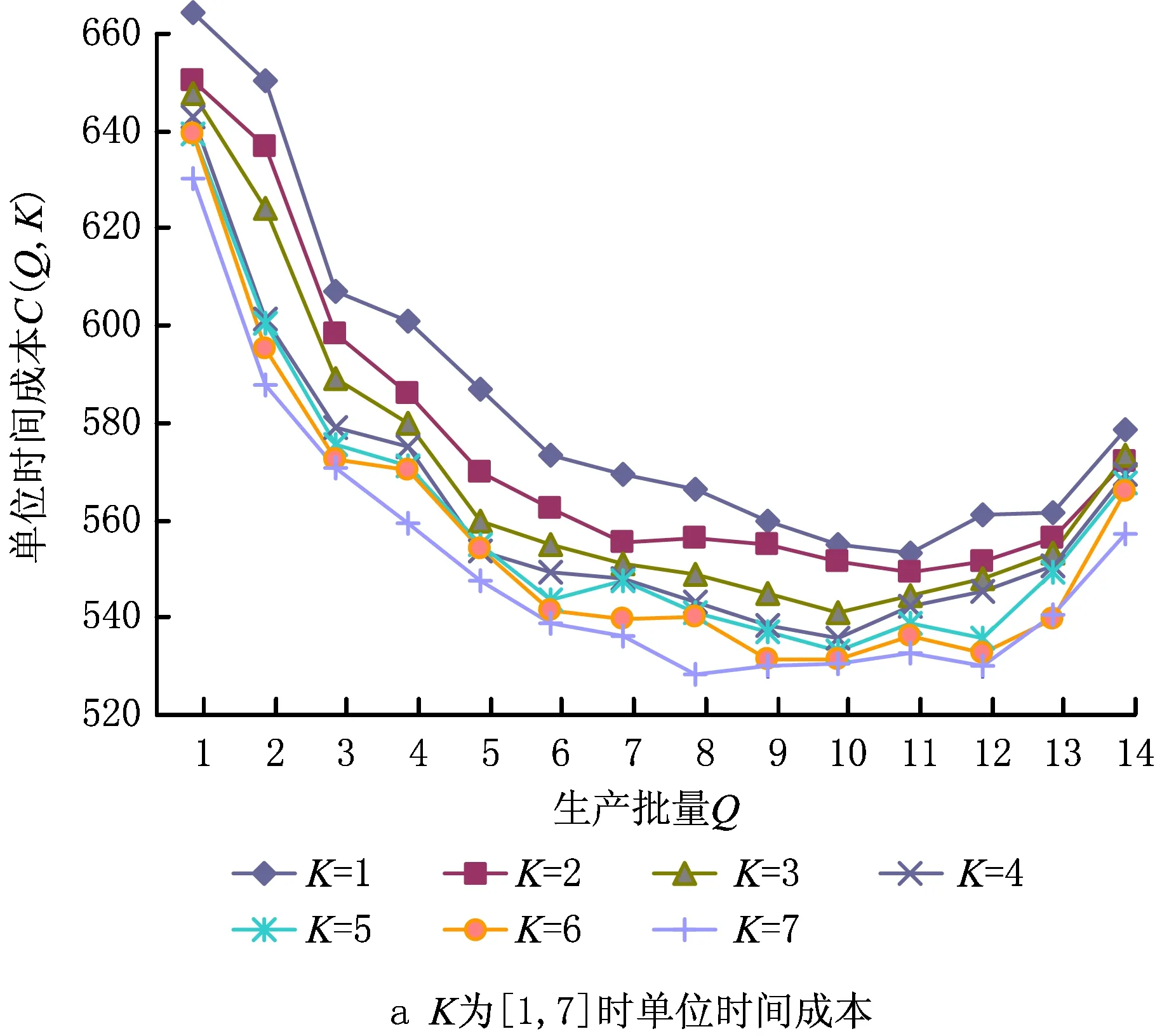
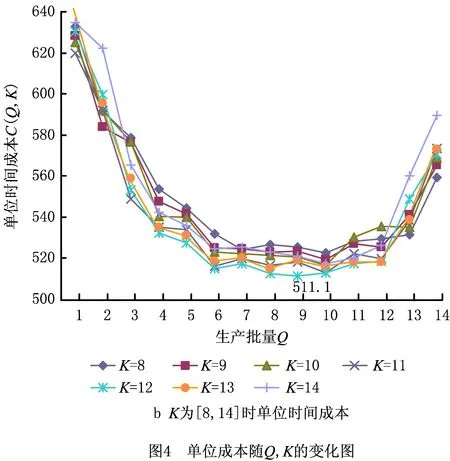
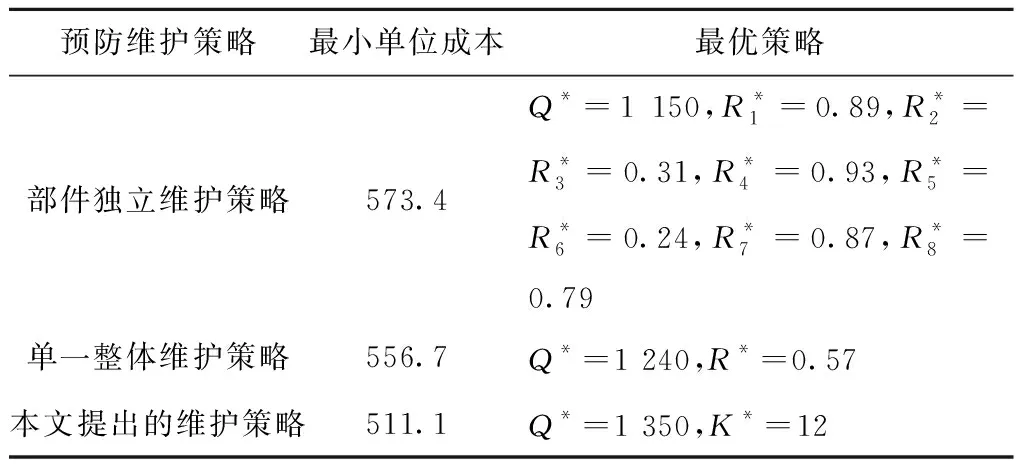
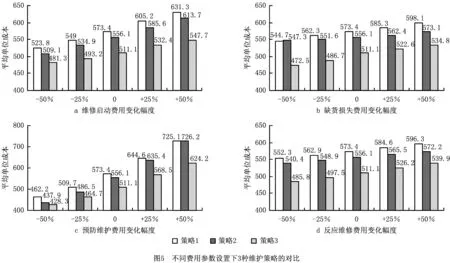
=P[Xj(tn)+X(τ) (2) (3) 关于维护效果,此处假设部件是修复非新的。对于寿命服从Weibull分布的部件而言,采用役龄递减因子法来刻画维修效果。设役龄递减因子为rik∈(0,1),则部件i在第k次预防维护后的故障率为 hi(k+1)(t)=hik(t+rikΔik), (4) 式中:Δik表示第k-1次维护与第k次维护的间隔时间(是一个批量生产时间τ的整数倍)。 对劣化进程为Gamma过程的部件,假设预防维护之后,劣化量不能恢复为零(修复非新),而是一个服从Beta分布的随机变量。设部件j在维护前检测到的劣化量为xj,则维护之后剩余的劣化量xj′服从区间[0,xj]上的Beta分布,其概率密度为 (5) 式中:pj>0,qj>0,1{·}为示性函数。 1.2.2 反应性维修策略 在生产系统运行过程中,各部件可能会随机发生故障。在一个复杂的系统中,各部件通过串联、并联、混联或冷(热)储备等方式连接。在并联子系统中,某单个部件的故障不会导致整个系统停机;另一方面,集束型设备是在真空、无尘的密闭环境中工作,若要对某个故障部件进行维修,势必会导致整个系统停机。因此,为保持生产过程的连续性,在不影响系统运行的前提下,对非关键部件的故障暂不作处理。如果关键部件发生故障,则系统停机,立即进行反应性维修(更换),利用这个维修机会,将前面发生故障的非关键部件一并进行维修。如果没有关键部件故障,则故障的非关键部件等到本次生产批量结束后进行维修。 系统的生产率为P,外部需求率为D(P>D),生产计划期为T,每个生产批量大小为Q。每个批量结束后,对系统进行检测、并做预防性维护(如有必要)。在系统停机维护期间,外部需求由库存来满足,若维护时间过长,库存不能满足需求,则产生缺货损失。维修活动结束且库存消耗完之后,系统重新启动开始下一批次的生产,即Non-Resumption策略[2]。一个生产周期定义为连续的两个生产批量开始时间的间隔,其中包括了批量生产时间、停机维护时间以及可能的空闲时间。一个生产周期内系统运行的进程如图2所示。图2a表示第n个批量生产结束后,对系统进行检测、维护,且维护在库存消耗完之前结束,下个批量待库存消耗完后开始生产。而图2b表示库存耗完时维护活动尚未结束,因此产生了缺货损失。图2c表示在第n个批量内系统发生故障,则立即进行反应性维修,且维修在库存消耗完前结束,下个批量待库存消耗完后开始生产。在图2d中,反应性维修在库存耗完后才结束,故产生了缺货损失。 (1)预防性维护不能使部件修复如新,而反应性维修(更换)可使部件恢复如新。设预防维护与反应维修所需时间均为随机变量。 (3)以csetup表示生产系统停机后重新启动的费用;ch表示单位产品在单位时间内的存储费用;cl表示单位时间的缺货损失。 (6) 设生产系统在第n个生产周期内的tn时刻发生随机故障,记SF(tn)为tn时刻所有发生故障的部件集合,包括了故障的关键部件和非关键部件。则反应维修总费用为固定费用部分c0与各部件的维修费用之和,即 (7) 第n个生产周期内的库存费用,如图2c所示,可表示为系统运行期间的存贮费用与系统停机时的存贮费用之和,即 (8) (9) (10) 反应性维修的总费用 (11) 类似第一种情形(即系统发生随机故障),由图2a可算得第n个生产周期内的库存费用 (12) (13) (14) 式中生产批量大小Q和预防性维护参数K为二维联合决策变量,本文的目标就是要寻找最优的(Q*,K*),使得平均单位时间成本C(Q,K)达到最低。 特别说明: (2)仿真参数Ns表示模拟仿真的次数,需足够大以使算法收敛,并取平均值作为单位成本的估计值。 (3)算法中TCM表示一次反应维修活动总时间(为各故障部件维修时间之和)、TPM表示一次预防维护活动总时间(为需要维护部件的维护时间之和)、Tidle表示当维护时间小于库存消耗时间时,系统空闲时间。 以某集束型设备为例,对最优经济生产批量与视情维护策略进行仿真实例验证。集束型设备主要包括以下组件:机械搬运手、氧化加工腔、离子注入腔、光刻加工腔、机械研磨腔、清洗腔。根据历史数据与先验知识,设维护时间与反应维修时间分别服从参数为λi、μi的指数分布,设备与维修参数如表1所示。 设集束型设备的生产率P=150单位/天、需求率D=120单位/天、生产计划期T=180天、设备的启动费csetup=800元/次、检测费cin=200元/次、预防性维护或反应性维修的启动费用c0=300元/次、库存存贮费用ch=0.3元/单位/天,缺货损失cl=10元/单位/天。预防维护之后部件的劣化剩余量服从Beta分布,其中的参数为p=0.4,q=1.2。 表1 系统各部件寿命分布/劣化机制与相关参数 取预防性维护参数K=(1,2,3,4,5,6,7,8,9,10,11,12,13,14),在不同的Q值下,单位成本C(Q,K)的变化规律如图4所示。当预防维护参数K=12、批量大小Q=1 350时,生产系统的单位成本最小,为511.1元/天。当集束型设备生产了1 350单位的晶圆时,对设备进行检测。部件1、4、7、8的预防维护阈值为12×0.07=0.84,即当它们的可靠性预测值低于0.84时,便进行预防性维护;部件2、3、5、6的预防维护阈值为12×0.23≈0.28,即当它们的可靠性预测值低于0.28时进行预防性维护。 作为对比,选取另外两种维护策略来与本文提出的预防维护策略来进行比较:①各部件独立维护策略[14],各部件的最优维护阈值Ri是各自独立优化的结果,未将其视为系统的一部分;②单一整体维护策略[15],将系统视为一个单一整体,确定其预防维护阈值R,未考虑部件之间的差异。根据表1中相同的模型参数设置,利用MATLAB遗传算法工具箱算得两种策略下的最优解及其对应的最小单位成本,如表2所示。从表2的数据可以看出,文中提出的维护策略较独立维护策略可节省10.9%的成本、较整体维护策略可节省8.1%的成本。其原因就在于,该维护策略不只是将系统视为一个整体,同时考虑了部件之间的差异及其在系统中的结构重要程度,弥补了其他两种策略的短板。 表2 3种预防维护策略下最优解的对比结果 考虑到维护策略的优劣可能还受到参数设置的影响,下面通过敏感性分析对以上3种策略进行更为全面的评价。图5a~图5d分别为维修启动费用、缺货损失、预防维护费用、反应维修费用改变幅度从-50%到+50%时对应的平均单位成本。图中策略1、2、3分别表示部件独立维护策略、单一整体维护策略以及文中所提出的维护策略。从图5可看出,策略3在4种情况下的表现均优于其他两种策略。具体阐明如下: (1)在图5a中,随着维修启动费用c0的增加,策略3较策略1、2的优势逐渐扩大,成本的节约幅度分别从8.1%、5.4%提高至13.2%和10.8%。这说明策略3避免了过度维护、减少了频繁启动维护费用。 (2)图5b与图5a呈现的结果正好相反,随着缺货损失cl的增加,策略3较策略1、2的优势逐渐减小,成本节约幅度分别从13.3%、13.7%降至10.6%和6.7%。这说明策略1、2较策略3在减少缺货损失方面具有优势,这是因为策略1、2更注重设备的预防维护,有效地减少了设备的突发故障,从而减少了被迫停机导致的缺货损失。 以多部件复杂生产系统为研究对象,建立了生产与维护的联合优化模型。对于多部件的复杂系统,在对各部件进行劣化建模时,根据其劣化机理恰当地选择随机变量或随机过程,不作统一的、无差别的处理。视情维护策略中包括设备检测周期和预防维护阈值两个关键因素。本文将批量大小作为决策变量,是基于以下两点考虑:①由于检测在批量生产结束后进行,故批量大小直接决定了设备检测周期,从而会影响维护策略;②本文的维护活动是以生产为驱动,批量大小(或生产时间长短)会影响设备的劣化进程。批量越大,设备在运行过程中故障风险越高。鉴于以上事实,批量大小对维护活动具有决定性的影响,故本文将其作为一个决策变量,连同维护阈值进行联合优化,并设计了仿真算法求得最优联合策略。通过集束型晶圆制造设备的实际生产、维护优化问题演示了本模型。敏感性分析的结果显示所提维护策略较部件独立维护策略及单一整体维护策略在减少总成本方面具有优势,特别是在维修启动费用和预防维护费用较高的情况下优势更为显著。因此,本文对于制造企业合理地制定生产计划和维护方案,降低运营成本具有一定的参考指导意义和参考价值。 本文只考虑了单产品不变需求的生产情形,为了使模型更加符合生产实际,在未来的研究中,笔者将进一步考虑多产品并且需求随机变动的情形,建立随机动态规划模型进行优化求解。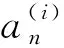
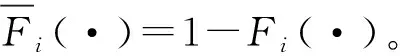
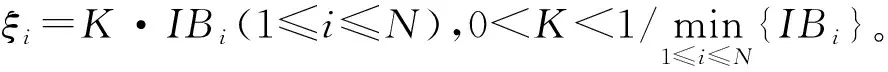
1.3 批量生产过程描述

1.4 符号与假设
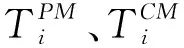
2 模型建立
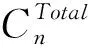
2.1 一个生产周期内系统发生故障时的各项费用
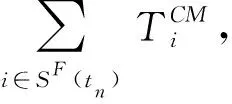
2.2 一个生产周期内系统未发生故障时的各项费用
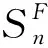
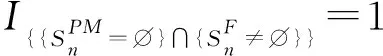

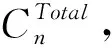
3 仿真算法
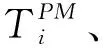
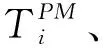
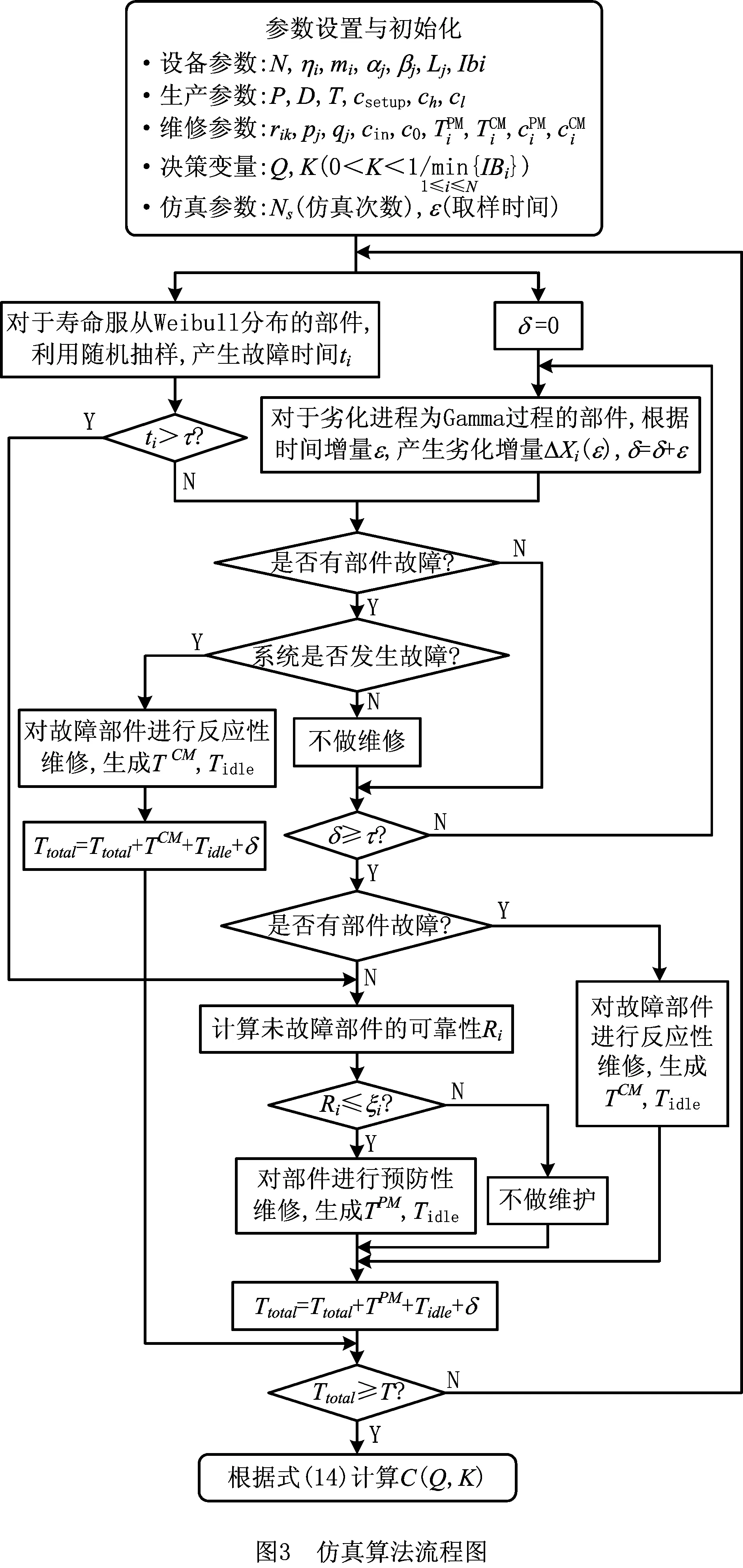
4 实验分析
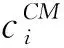
5 结束语
