基于跳度约束的连续短线段高速加工运动学平滑算法

杜金锋，张立强，高 甜

(上海工程技术大学 机械工程学院，上海 201620)

0 引言

数控(Numerical Control, NC)系统在加工由连续短线段组成的刀具路径时，生成多个连续的点对点(P2P)运动加工的NC程序，NC程序所规定的刀具路径是位置(G0)连续。如果直接进行加工，机床进给轴进给到路径拐角处就必须减速停止，转变进给方向后再加速进给，这就导致机床进给轴频繁启停，引起刀具振动，降低加工质量。针对该问题，有专家学者提出样条曲线插补技术，即在连续短线段刀具路径拐角处插入高阶样条曲线，根据样条曲线计算出进给轴在拐角处的最佳转接速度，再对拐角间的短线段进行速度规划，使得在加工过程中机床进给轴速度和加速度可以平滑转接，有效减少刀具振动、提高加工质量。张君等[1]用曲率连续的NURBS曲线平滑刀具路径中的拐角，再采用7段和5段混合的双向S型加减速控制算法进行速度规划。张晓辉等[2]建立拐角曲线过渡插补算法来确定连续短线段刀具轨迹的速度极小值点和该点的速度。何均等[3]参考连续短线段刀具路径转接的几何约束、运动约束、转接参数计算和空间圆弧插补等理论，提出圆弧转接数学模型以实现高速连续短线段插补。

但是对连续短线段刀具路径进行样条曲线插补并不能广泛应用于数控系统，因为平滑的高阶样条曲线在插补过程中需要大量复杂计算。大多数NC系统无法满足实时高效内插高阶样条曲线的硬件要求，而且高阶样条曲线插补技术还存在一些技术瓶颈，如：精确计算曲线长度、高效规划进给速度和实时插值过程中有效抑制弦高误差等。因此，有些专家学者直接研究伺服轴的运动学平滑技术，使得在拐角处各伺服轴的轮廓轨迹混合生成的刀具路径平滑转接，在提高加工效率和加工质量的同时消除高阶样条曲线插补的需求。黄昕等[4]根据小线段中进给速度约束条件，采用基于双向扫描算法确定小线段拐角处的最优进给速度。冷洪滨等[5]提出一种三次多项式型加减速自适应插补算法，以提高微细加工的加工质量。Duan等[6]使用最优控制生成时间最佳的转弯轨迹。Tsai等[7]研究伺服轴在拐角处生成的混合路径，提高拐角的动态轮廓精度。Tajima等[8]针对轨迹中的拐角提出跃度约束的运动学平滑算法，实现进给轴在拐角处的最优运动。

本文在现有伺服轴运动学平滑技术的基础上，针对连续短线段刀具路径提出跳度约束加速度曲线[9]的运动学平滑算法。跳度为加速度的二阶导数，对跳度曲线进行二次积分可得到加速度曲线，使用跳度约束可以消除加速度曲线上的奇异点，使得加速度曲线更加平滑，在加工过程中，可以有效减少刀具振动、提高加工质量。该算法针对连续短线段刀具路径的拐角和拐角间的短线段，利用跳度约束加速度曲线并对其附加速度、加速度和位移边界条件约束，结合最大轮廓误差和驱动器的运动学限制，推导出拐角处的最佳转接速度和短线段路径的最大进给速度，最终实现在整个刀具路径中进给轴速度和加速度平滑转接。最后对所提算法进行实验分析，并通过对比直线加减速算法来验证本文算法的有效性。

1 运动学平滑算法

1.1 跳度约束加速度曲线

跳度约束加速曲线已被证实在减少机床振动和提高加工质量方面存在显著优越性[9]，它可以产生平滑的速度和加速度转变。跳度约束加速度曲线如图1所示，在分段跳度极限Sm下，已知初始速度Vs和初始加速度As，则可以通过对跳度曲线S(t)积分来获得跃度j(t)、加速度a(t)、速度v(t)和位移r(t)的计算公式，如式(1)：

(1)

由公式可以得出位移曲线四次可微，则位移曲线G3连续，速度曲线三次可微，则速度曲线G2连续，加速度曲线二次可微，则加速度曲线G1连续。

式(2)～式(6)为相应的跃度、加速度、速度、位移计算公式。

(2)

(3)

(4)

(5)

(6)

其中t表示绝对时间，t1、t2表示每个阶段的时间边界。Sm为驱动器的跳度极限。Tk(k=1、2)是对应的时间参数，其从k个阶段的开始处计时。Ak表示相应阶段结束时所能达到的加速度，Vk表示相应阶段结束时所能到达的速度，Rk表示相应阶段结束时所能达到的位移。减速阶段的公式只需用负跳度替换正跳度即可得到。

1.2 拐角处运动学平滑算法

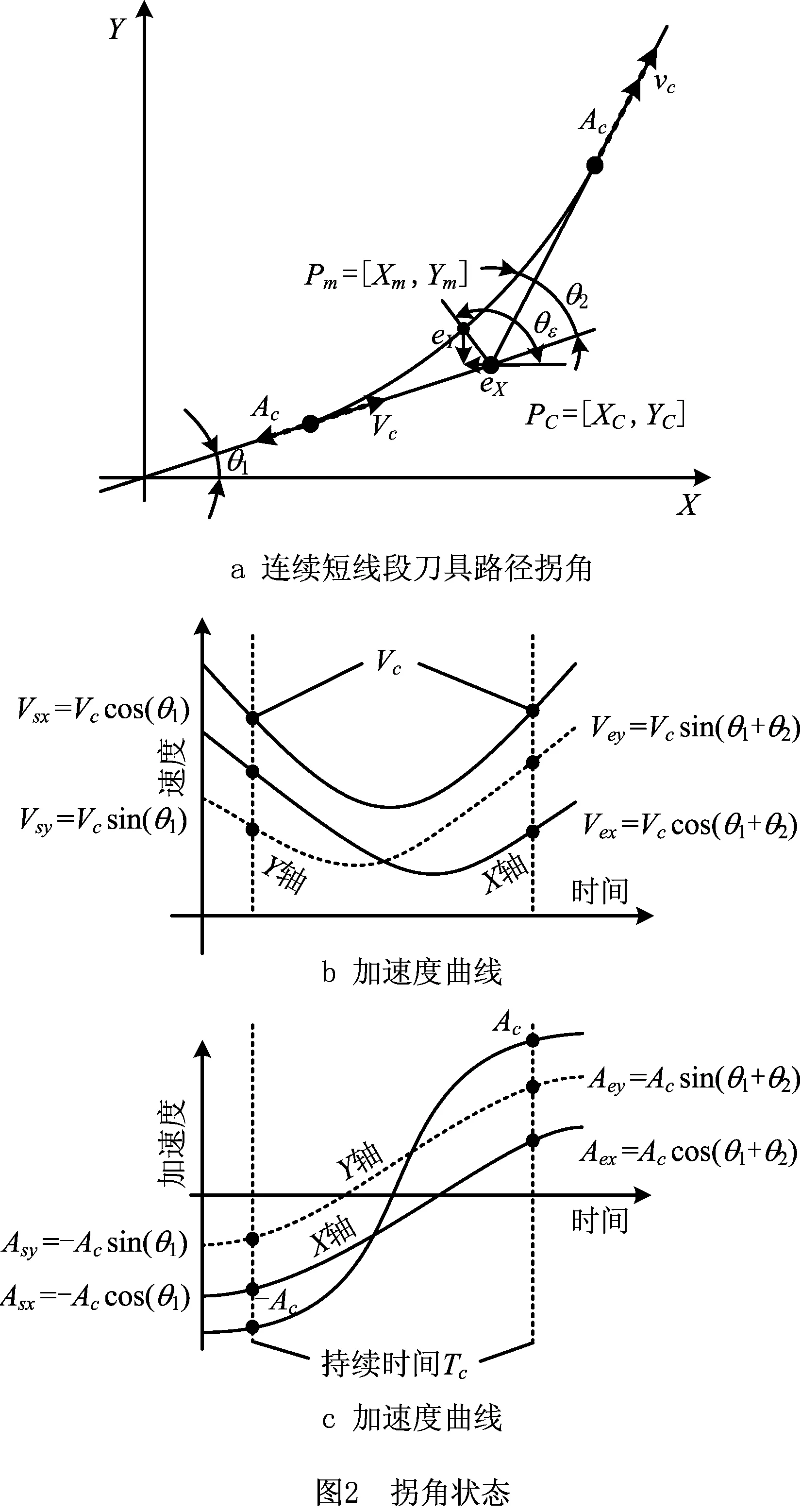
针对连续短线段刀具路径中的拐角，对跳度约束加速度曲线附加速度、加速度和轮廓误差边界条件，在满足驱动器运动学限制条件下推导最佳转接速度，再根据速度、位移公式得出各个轴的加速度、速度、位移曲线。在X-Y平面上，刀具路径的拐角状态如图2a 所示，两个方向为θ1和θ1+θ2的线性段在Pc=[Xc,Yc]处相交形成拐角。线性段的单位矢量ts=[cos(θ1)，sin(θ1)]T和te=[cos(θ1+θ2)，sin(θ1+θ2)]T。在拐角和直线段的转接点处，对进给轴施加速度和加速度边界条件，进入拐角转接点处的速度和加速度为Vc和-Ac，离开拐角转接点处速度和加速度为Vc和Ac，如图2b所示。通过边界条件约束得到各个轴的速度曲线，通过速度曲线求得各个轴的进给轮廓，从而得到刀具的运动轮廓轨迹，该轮廓轨迹偏离原始加工路径，最大的轮廓误差ε发生在轨迹中点Pm=[Xm,Ym]处，εx=εcos(θε)，εy=εsin(θε)是轮廓误差的笛卡尔投影，且θε=π/2+θ1+θ2/2。式(7)～式(11)为各个轴的跳度、跃度、加速度、速度和位移曲线

(7)

(8)

(9)

(10)

(11)

式(12)和式(13)为拐角开始处和结束处的速度和加速度。拐角开始处和结束处的速度方向相同，加速度方向相反，可获得对称的轮廓轨迹，最大轮廓误差在轮廓的中点。

(12)

(13)

拐角期间，每个轴的速度变化可由式(10)、式(12)得出：

(14)

因为最大轮廓误差在轮廓的中点，中点位置可以由式(11)得出：

(15)

拐角Pc的几何位置定义为：

(16)

其中Rc为进入拐角转接点到拐角的欧几里得长度，其可以通过轮廓轨迹的几何形状和总位移来计算。例如X轴的运动，Rc可以由式(10)和式(11)推导出：

(17)

由式(15)～式(17)可以得到轮廓误差约束：

εx=xmid-xC=εcos(θε)=

(18)

类似地，Y轴的各个参数可以通过余弦项替换正弦项得出。在NC系统加工过程中，为了提升加工效率，至少有一个轴的加速度和跳度达到驱动器运动学限制极限，这个轴就是限制轴，基于式(14)来确定最大速度跃变轴就是限制轴，从而推导出最佳转接速度。例如ΔVX>ΔVY，X轴就是限制轴。该轴的加速度、速度和最大轮廓误差约束为：

VCcos(θ1+θ2)=VCcos(θ1)-2ACcos(θ1)

(VCcos(θ1)T1(cos(θ1+θ2)-cos(θ1))-

cos(θ1)+cos(θ1+θ2)。

(19)

通过限制驱动器加速度或跳度极限推导最佳转接速度。对于CNC数控系统，各个轴的跳度极限都相同，Smax=Sxmax=Symax。假设限制轴以驱动器最大跳度极限进给，则将Sx=Sxmax带入式(19)求得最佳转接速度为：

(20)

各个轴的加速度极限相同，Amax=Axmax=Aymax。当将限制轴以驱动器最大加速度进给时，则Ax=Amax带入式(19)求得最佳转接速度为：

(21)

为了满足驱动器的运动学限制条件，最佳转接速度为：

VC=min{VCSmax,VCAmax}。

(22)

最后，根据式(19)求解进给轴转接运动的持续时间：

(23)

对限制轴进行速度规划后，从动轴转接持续时间和限制轴相同，从动轴的跳度和加速度极限分别由式(12)和式(13)推导出：

(24)

(25)

由式(7)～式(11)可得出从动轴的速度、加速度和位移曲线，将X、Y轴的运动轨迹混合则得到刀具的轮廓轨迹。

1.3 拐角间的直线段运动学平滑算法

在连续短线段刀具路径中，拐角间的直线段可根据进给轴的速度和加速度转接规律分为3段(如图3)：①进给轴速度在平滑减少的加速度条件下从最佳转接速度VC1加速至驱动器速度极限Vm，该段结束时加速度减少至0 mm/s2，该段的欧几里得长度为R1;②进给轴在驱动器速度极限下恒速进给，该段的欧几里得长度为R3;③进给轴速度在平滑增加的负加速度条件下从驱动器速度极限Vm减速至最佳转接速度VC2，该段结束时加速度增加至-AC2，该段的欧几里得长度为R3。如果拐角间的直线段较短，驱动器在加速度极限条件下，没有足够的路径进给到驱动器的速度极限，则必须调整进给轴的最大进给速度Vm，此时第①段欧几里得长度R3=0，通过对第①段、第③段的进给轴附加速度、加速度和位移约束，可推导出进给轴在连续短线段刀具路径拐角间直线段的最大进给速度Vm。

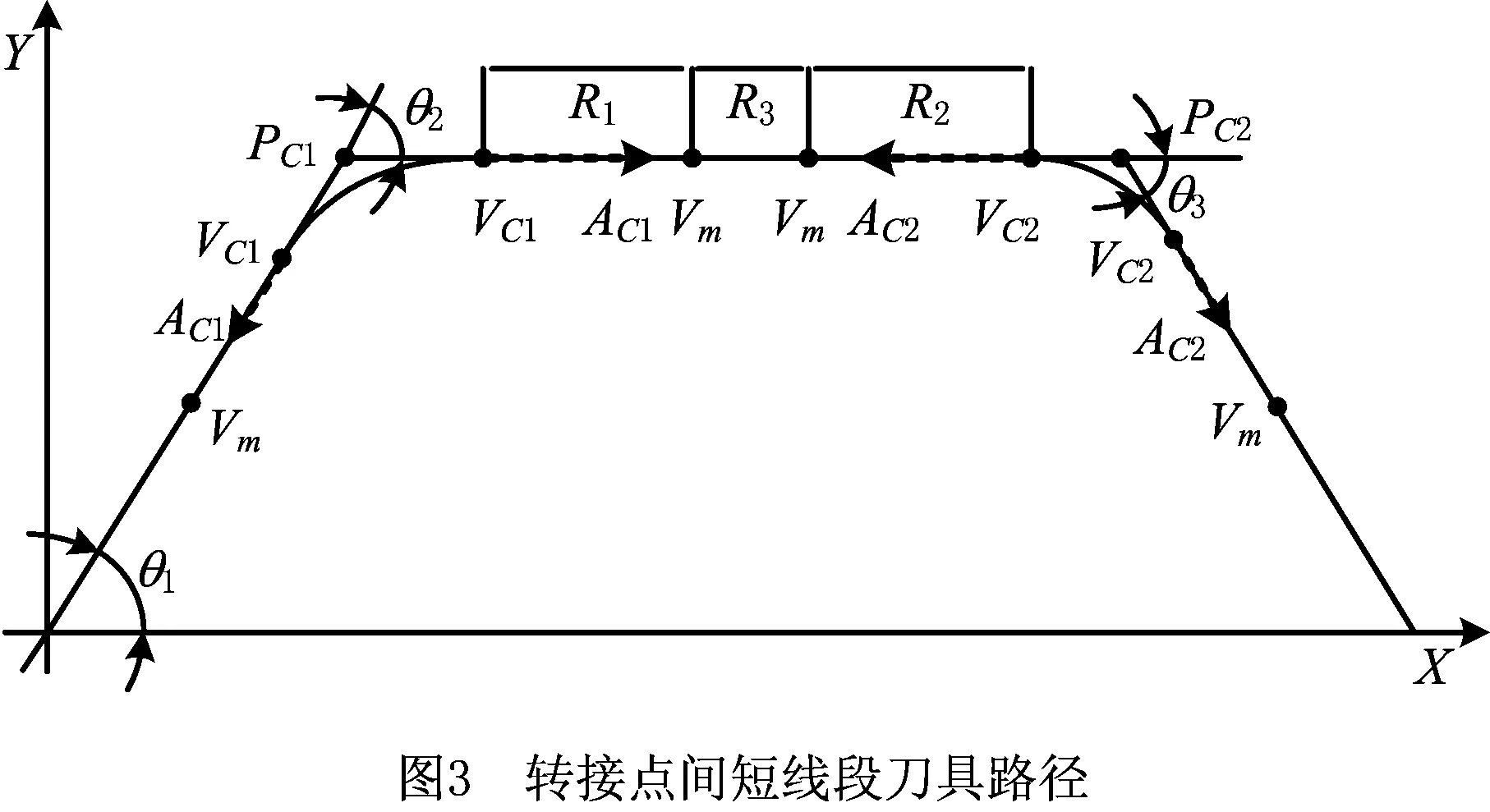
由1.2节可以推导出拐角PC1和拐角PC2的最佳转接速度VC1和VC2。为了使得在拐角和直线段间的速度和加速度平滑转接，没有奇异点，规定在直线段开始处，进给轴的速度为VC1、加速度为AC1，直线段结束处，进给轴的速度为VC2、加速度为-AC2。

在第①段利用跳度限制加速度曲线使得进给轴速度平滑转变到驱动器的最大速度极限Vm，在驱动器跳度极限条件下，加速度可以在一定时间内从AC1减速到0，但速度在相同时间内无法达到驱动器速度极限Vm，这就需要在加速度极限AC1条件下恒加速度加速一定时间，该段时间为T1，可由式(9)和式(10)推出：

(26)

则第②段的速度曲线为：

(27)

在第③段利用跳度限制加速度曲线使得进给轴速度平滑转变到拐角2的最佳转接速度VC2，在驱动器跳度极限条件下，加速度可以在一定时间内从0加速到-AC2，但速度在相同时间内无法达到最佳转接速度VC2，这就需要在加速度极限-AC2条件下恒加速度减速一定时间，该段时间为T3，可由式(9)和式(10)推出：

(28)

则第③段的速度曲线为：

(29)

由式(11)、式(17)、式(26)、式(27)可得第①段欧几里得长度

(30)

由式(11)、式(17)、式(28)、式(29)可得第③段欧几里得长度

(31)

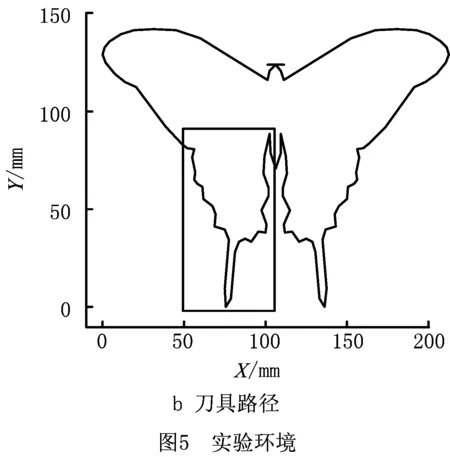
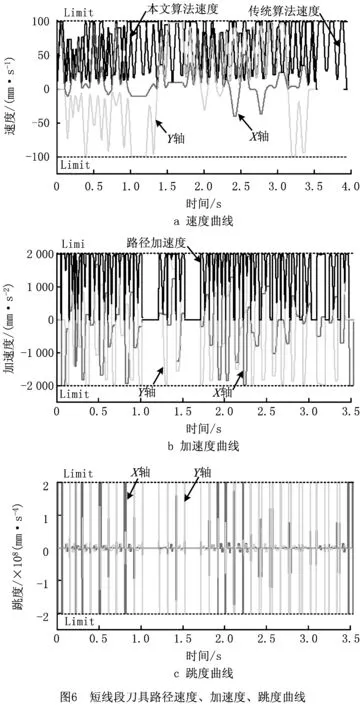
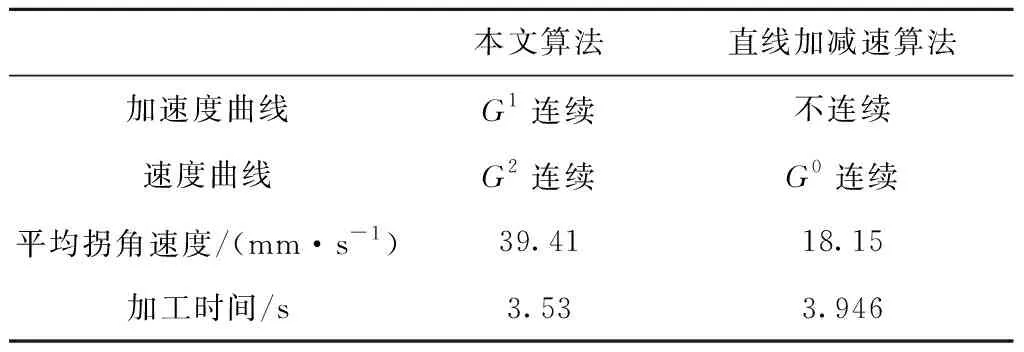
如果连续短线段刀具路径拐角间的直线段欧几里得长度L

Vm=

(32)

图4为运动学平滑算法的流程图。从该算法的推导中可知，其基于跳度约束加速度曲线，生成的进给轮廓四次可微，可达到G3连续，生成的速度曲线可达到G2连续，生成的加速度曲线可达到G1连续。

2 仿真分析

为验证在连续短线段刀具路径中基于跳度约束加速度曲线平滑速度和加速度算法的有效性，对连续短线段刀具路径速度和加速度平滑算法进行实验分析，并通过对比直线加减速算法验证算法的有效性。

实验所用X-Y数控系统如图5a所示，平面运动由两个线性电机驱动，其中Y轴被设计成龙门架，龙门架承载较轻的X轴，伺服放大器被设置为转矩(电流)控制模式下操作，线性编码器的反馈分辨率为0.712 5um，伺服系统的闭环采样时间为0.1 ms，X、Y轴的位置反馈带宽为ωn=35 Hz，以确保良好的位置同步和路径跟踪。实验的刀具路径如图5b所示，为一蝴蝶轮廓，刀具路径总长842.7 mm，共96个拐角，为了突出算法对连续短线段刀具路径的有效性，对蝴蝶刀具路径的翅膀尾部短线段刀具路径进行分析，即方框中的刀具路径，该框图中的刀具路径总长216.46 mm，共29个拐角，最小线性段为2.78 mm，最小拐角24.23°，最大拐角173.21°。设定所有拐角制造公差为20 um，进给轴最大进给速度100 mm/s，最大加速度限制为2 000 mm/s2，最大跳度限制为2×108mm/s4。实验参数曲线如图6所示。

通过对比直线加减速算法，本文提出的速度和加速度平滑算法具有更优异的加工性能和更高效的加工效率，能够有效避免速度和加速度突变引起的刀具振动和过切。实验结果如表1所示，对于该段连续短线段刀具路径，采用本文算法的刀具路径曲线达到G3连续，速度曲线达到G2连续，加速度曲线达到G1连续，实现进给轴速度和加速度的平滑转接，在转接速度方面，平均转接速度由18.15 mm/s提升至39.41 mm/s，显著提高了转接速度。在加工时间方面，采用本文算法比传统直线加减速算法加工时间减少了0.42 s，加工周期时间减少了11%。考虑到在较长连续短线段刀具路径(例如在高速铣削和精细雕刻中所使用的刀具路径)可能包含数百上千个尖角，加工时间可以显著减少，加工效率得到提高。

表1 实验结果分析

3 结束语

本文针对连续短线段刀具路径加工过程中，机床进给轴速度和加速度突变引起刀具振动和过切等问题，提出基于跳度约束加速度的运动学平滑算法。该算法针对连续短线段刀具路径，对跳度约束加速度曲线施加边界约束，并结合最大轮廓误差和驱动器的运动学限制，推导出进给轴的最佳转接速度和最大进给速度，最终实现在连续短线段刀具路径加工时进给轴速度和加速度平滑转接。通过实验对比直线加减速算法，本文算法在转接速度和加工时间等方面均有显著的提升。在高速铣削或精细雕刻等较长刀具路径的加工中，可以提高加工效率和加工质量。在今后的研究中将进一步考虑动力学因素，并将进给补偿和误差预测纳入到算法中以提高加工质量。