基于遗传算法的双层喷涂自动轨迹规划

卢晓冬，唐 倩+，蒋 敏,熊 浩，宋 军，黄 耀

(1.重庆大学 机械传动国家重点实验室，重庆 400044;2. 成都飞机工业(集团)有限责任公司 610092)

0 引言

在现代制造业中，表面喷涂技术得到了广泛应用[1]，产品表面涂层的厚度及其均匀性对产品质量、性能和寿命有着重要影响。随着机器人技术和计算机技术的迅速发展，机器人喷涂逐渐代替了手工喷涂。在机器人喷涂过程中，喷涂轨迹直接影响产品表面涂层厚度及其均匀性，是研究热点之一[2-3]。目前，机器人喷涂轨迹规划方法主要有示教法和自动轨迹规划法两种。示教法虽然规划方法简单，但费时费料，且涂层均匀性主要取决于操作人员的技能水平。自动轨迹规划以涂层分布模型、工件模型为基础，按照相应约束条件和优化准则，自动规划喷涂轨迹，克服了示教法的弊端，提高了喷涂效率和喷涂质量。近年来，国内外众多专家学者也都进行了相应的研究。凯特林大学的Sheng等[4]对复杂曲面上的自动喷涂轨迹规划与优化算法展开了初步研究。德克萨斯州立大学的Chen等[5]对工件表面网格化CAD模型进行了分片处理，提出片与片之间的连接算法。维斯瓦力亚国家技术研究所的Andulkar等[6]提出了增量式离线喷涂轨迹规划算法，并对喷涂速度、涂层重叠宽度进行优化，提高了涂层厚度分布的均匀性。清华大学陈雁等[7]基于抛物线喷涂模型对工件表面涂层均匀性进行了分析。清华大学缪东晶等[8]基于数控刀位轨迹生成的方法对喷涂轨迹进行了自动规划研究，并对喷涂速度进行优化，提高了喷涂质量。

分析当前研究现状可知，目前的自动喷涂轨迹规划大都是等喷涂间隔、等喷涂速度、等喷涂距离的单层喷涂，对双层喷涂自动轨迹规划的研究并不多[9]。然而，现代工业对产品表面涂层的要求越来越高，越来越多的工件不仅要求涂层较厚，还要求严格控制涂层均匀性，采用单层喷涂往往不能满足要求，必须进行双层甚至多层喷涂。如果只是简单地将单层喷涂自动轨迹规划结果叠加应用于双层喷涂，并不能达到最佳效果。本文针对表面喷涂技术涂层均匀性问题，提出一种双层喷涂自动轨迹规划方法，该方法实现流程如图1所示。首先在椭圆双β分布模型[10]基础上，建立了一个考虑喷涂距离的立体涂层累积速率模型；然后利用微分投影法，将所得立体涂层累积速率模型映射到不同造型的工件表面，得到相应工件表面涂层累积速率模型；进一步，将工件表面涂层累积速率模型在喷涂时间上进行积分，得到喷涂后工件表面涂层厚度分布模型；最后，针对所得到的涂层厚度分布模型，以喷涂后各点厚度值与理想值的方差最小为目标，采用遗传算法进行求解，得到双层喷涂轨迹。通过在平面和圆柱面上的仿真分析和喷涂实验，验证了该方法在喷涂均匀性上的提升。

1 立体涂层累积速率模型建立

喷涂机器人自动轨迹规划的首要问题就是喷枪数学模型的建立。喷枪数学模型即涂层累积速率模型，反映了喷枪轴线垂直于某平面进行静态喷涂时，单位喷涂时间内该平面上某点处涂层厚度与该点所在平面位置的函数关系。目前，学者们主要提出两类喷枪数学模型：①无限范围模型，如柯西分布模型和高斯分布模型；②有限范围模型，如β分布模型，分段函数模型和椭圆双β分布模型[11-14]。相比其他模型，椭圆双β分布模型更能满足实际喷涂作业，故应用广泛。椭圆双β分布模型示意图如图2所示，由喷嘴喷出的涂料充分雾化，在空间内形成一个椭圆锥体区域，此时涂料在与喷枪轴线垂直、距离为

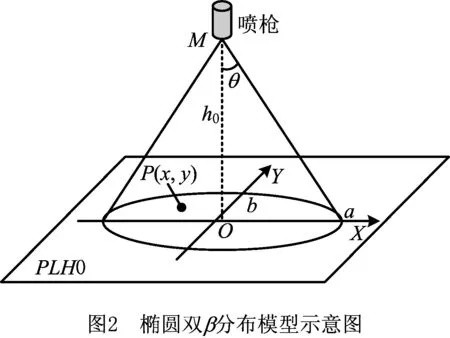
h0处的喷涂表面PLH0处的分布区域为一个以a为长轴，b为短轴的椭圆形。

喷涂表面PLH0内任意一点P(x,y)在单位喷涂时间下的涂层厚度分布模型，即涂层累积速率模型为

(1)

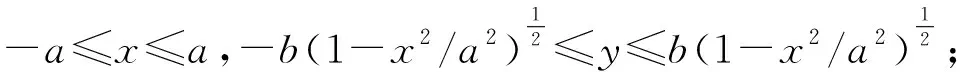
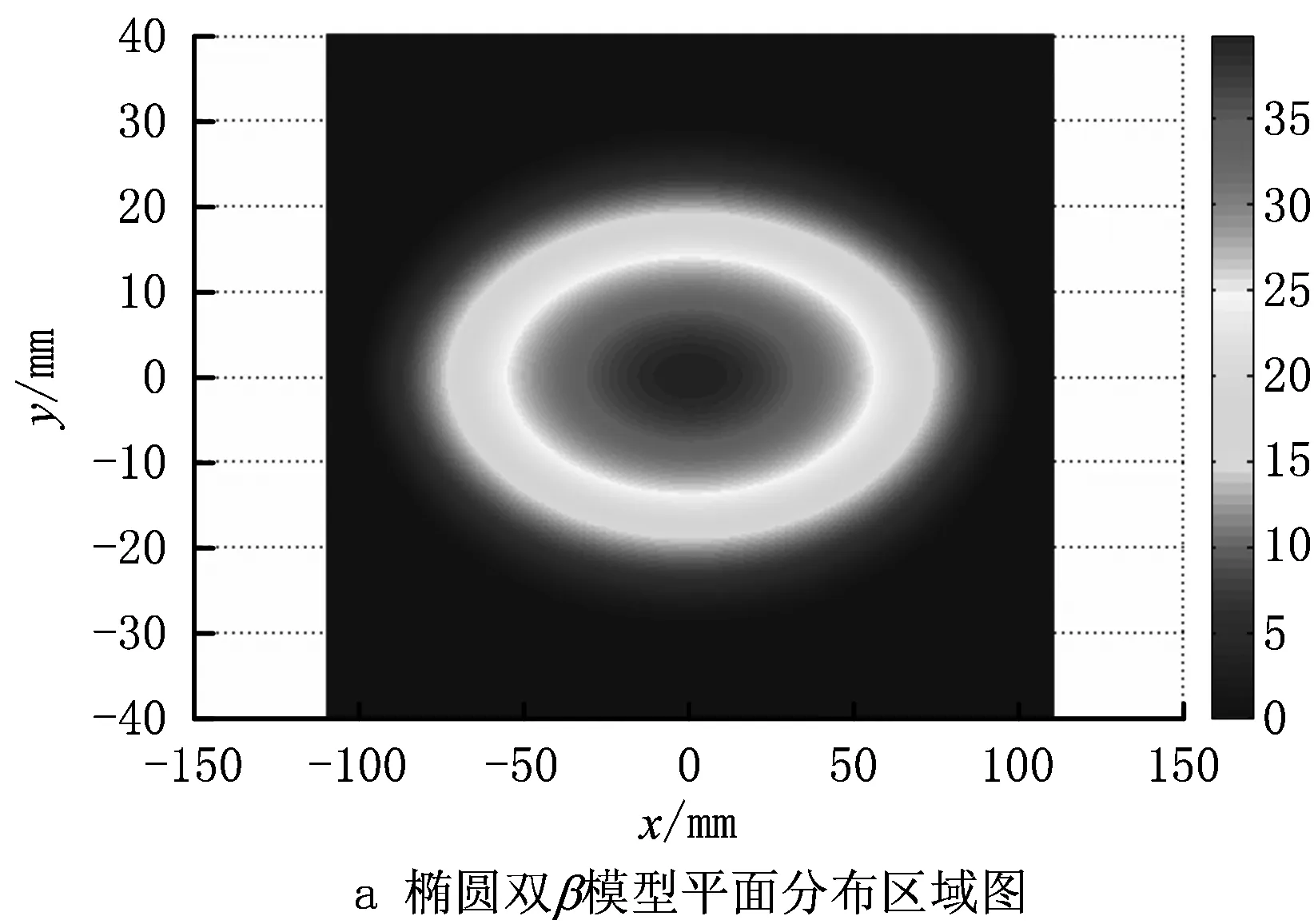
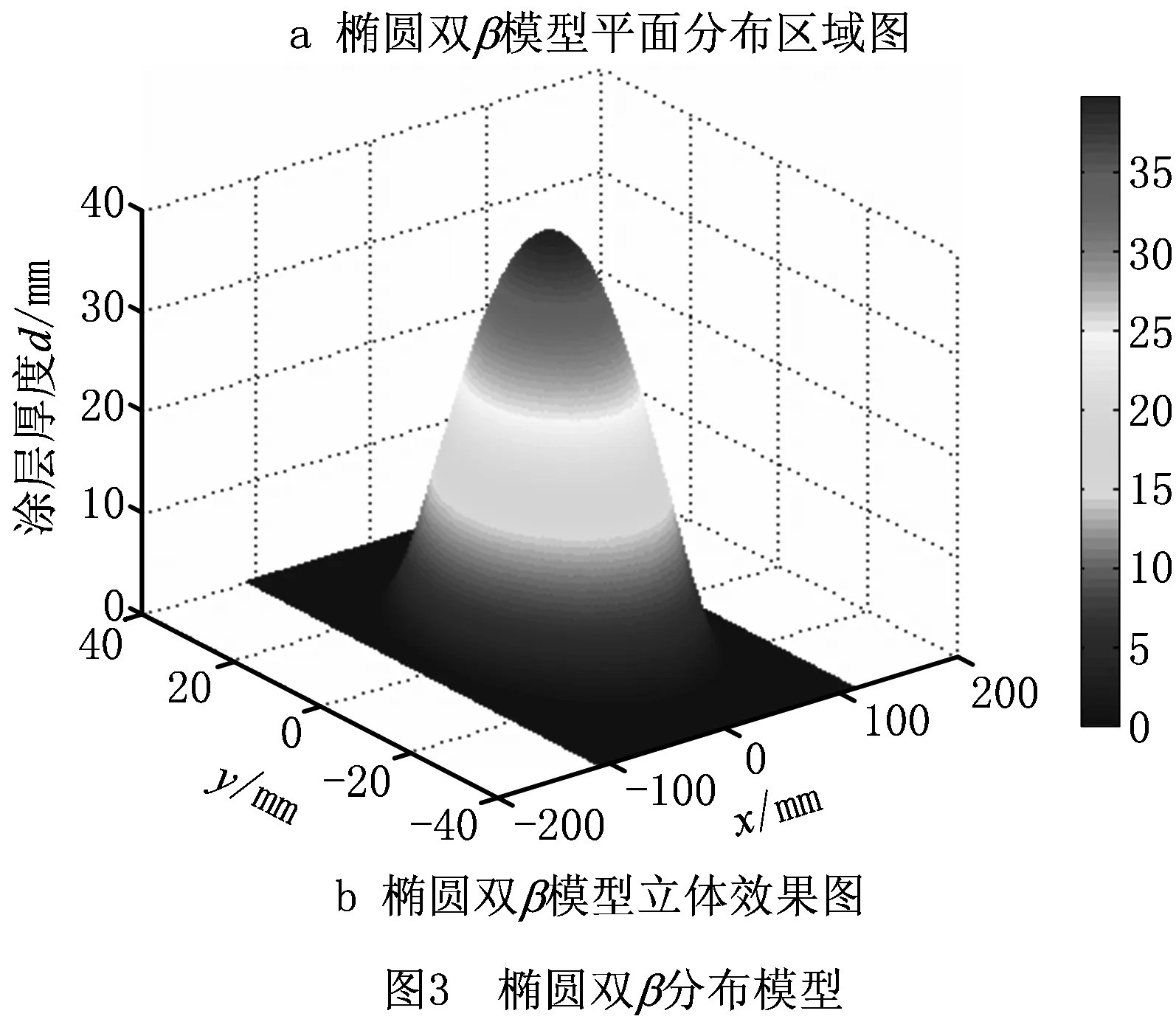
双层喷涂自动轨迹规划时，前后两层喷涂过程中，喷枪中心点至工件表面的喷涂距离h不同，从而导致涂层累积速率不同。而椭圆双β模型并未考虑喷涂距离h对涂层累积速率模型的影响，需要加以修正。运用微分投影法，将喷涂表面PLH0上的椭圆双β分布模型映射到不同喷涂距离h下的喷涂表面，得到一个考虑喷涂距离的立体涂层累积速率模型。

如图4所示，M是喷枪中心点；PLH0是与喷枪轴线垂直且距离为h0的平面；PLH1是与喷枪轴线垂直且距离为h1的平面；P0是喷枪中心点M沿任一喷射方向在实验平面PLH0的投影点；P是直线MP0与平面PLH1的交点；β是直线MP0与喷枪轴线之间的夹角；c0是在过点P0且垂直于直线MP0的平面上，以P0为圆心，Δr为半径的小圆；c是c0在平面PLH1下的中心投影，因为PLH0与PLH1平行，所以c是以P为圆心，Δr1为半径的圆。

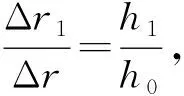
根据椭圆双β分布模型，当喷涂距离为h0时，涂层累积速率模型为

(2)

根据式(2)，结合P点与P0点厚度及坐标关系，得到不同喷涂距离h时立体涂层厚度模型为

(3)

2 平面双层喷涂自动轨迹规划

2.1 平面双层喷涂后涂层厚度分布

立体涂层累积速率模型反映了不同喷涂距离下，喷枪轴线垂直于某平面进行静态喷涂时，单位喷涂时间内该平面上某点处涂层厚度与该点所在平面位置的函数关系。当工件表面为平面时，式(3)即为工件表面涂层累积速率模型。通过对工件表面涂层累积速率模型在喷涂时间上进行积分，即可得到喷涂后涂层厚度分布模型。目前喷涂机器人典型的喷枪路径主要有Z型、X型、三角形等。其中Z型路径具有应用范围广、计算周期短等优点，本文以Z型路径为基础展开研究。平面双层喷涂轨迹示意图如图5所示。其中：第1层为“Z”形轨迹，喷枪轴线垂直于平面，任意两道相邻轨迹重叠宽度为d1，喷涂距离为h0，喷涂速度为v1；第2层也为“Z”形轨迹，喷枪中心位于第1层喷涂两相邻轨迹中间位置，喷枪轴线垂直于平面，喷涂距离为h2，喷涂速度为v2。对于喷涂平面某点而言，共经历了3道喷涂行程：第1层有两道，重叠宽度为d1，第2层有一道，位于第1层两道喷涂行程中间位置。可以看出，双层喷涂后，平面上的涂层厚度分布由若干个涂层厚度分布完全相同的带状区域组成，带状区域宽度为2a0-d1。可选取喷涂起始位置第一块带状区域进行规划，减少计算量。

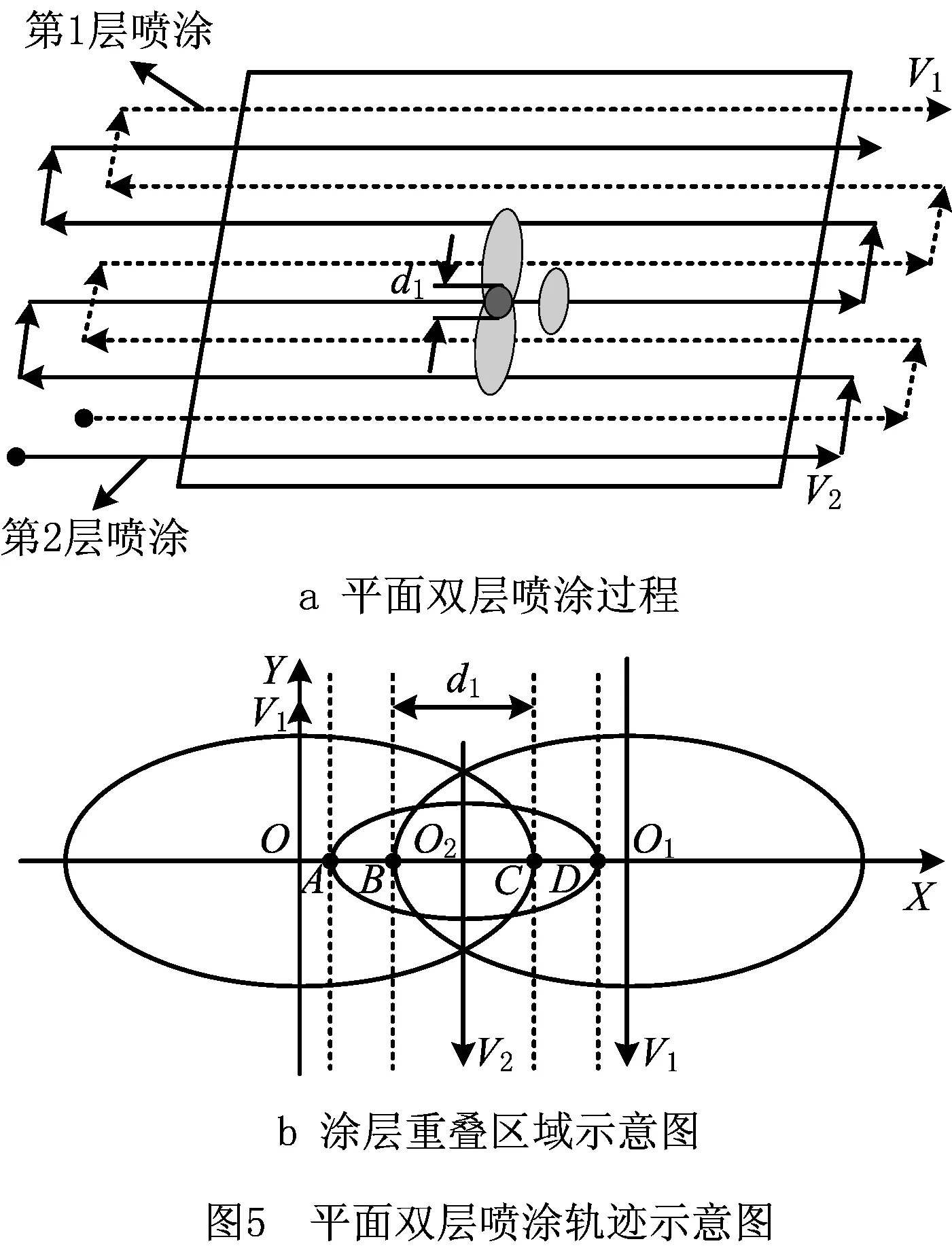
图5中：O、A、O2、B、C、D和O1的坐标分别为O(0,0)，A(a0-d1/2-a2,0)，B(a0-d1,0)，O2(a0-d1/2)，C(a0,0)，D(a0-d1/2+a1,0)，o1(2a0-d1)；d1为第1层喷涂任意两道相邻轨迹重叠宽度，a0和a2分别为第1层和第2层喷涂区域长轴长。

(4)

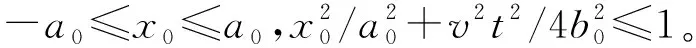
根据式(4)，用D1a(x,v1)表示第1层第1道喷涂行程在表面P点形成的涂层厚度，则第1层第2道喷涂行程在表面P点形成的涂层厚度D1b(x,d1,v1)可由D1a(x,v1)在X向偏移2a0-d1得到；同理将式(3)中喷涂距离h的值由h0改为h2,喷涂速度v的值由v1改为v2，并在喷涂时间上积分，即可用D2(x,v2,h2)表示第2层的喷涂行程在P点形成的涂层厚度。由此可得平面双层喷涂后表面点P的涂层厚度分布函数为：

(5)

2.2 平面双层喷涂轨迹优化目标函数

由式(5)可知，平面双层喷涂后不同位置处，涂层厚度分布与d1、v1、h2和v2这4个参数相关。得到均匀的涂层厚度的关键，在于规划好合理的d1、v1、h2和v2。相较于目前常用的单层喷涂，本文引入了第2层喷涂的喷涂距离h2和喷涂速度v2两个优化变量。针对这一优化问题，在0～2a0-d1之间，每隔1 mm选取一个点，n为总点数，以喷涂后这些点的涂层厚度值Di与理想涂层厚度值DA之间的方差最小为优化目标建立如下优化函数：

(6)

结合喷涂经验及设备性能，对d1、v1、h2和v2进行如下约束：d1∈[1,100]；v1∈[5,250]；h2∈[150,300]；v2∈[5,250]。

2.3 遗传算法求解及仿真

可以看出，平面双层喷涂轨迹优化是一个非线性、多变量、强耦合的较为复杂的数学问题，常规求解方法不但耗费时间，而且很难得出理想结果，为解决这一问题，选用遗传算法对其进行求解[15]，过程如下：

(1)涂层厚度分布模型参数选取 喷涂距离h0=300 mm，a0=100.668 mm，b0=30.912 mm，Dmax0=39.800 mm，β1=2.331，β2=3.139，DA=50 um。

(2)遗传算法参数选取 适应度函数为式(6)，4个变量的取值范围下界为[1,5 150,5]，上界为[100,250,300,250]；种群规模为50，初始种群随机产生；适应度尺度变换为排序方式；选择方式为随机均匀分布；精英个数为4，交叉率为0.8；变异函数为高斯函数；交叉方式为多点交叉；迁移方向为前向，迁移率为0.2，迁移间隔为20；最大代数为800，适应度限为无穷小，停滞代数为50。

(3)优化结果 算法在执行了440代之后结束，得到最优解为[50.382，27.474，224.929，128.675]，即第1层喷涂任意两道相邻轨迹重叠宽度d1=50.382 mm，喷涂速度v1=27.474 mm/s；第2层喷涂距离h2=224.929 mm，喷涂速度v2=128.675 mm/s，此时涂层厚度分布如图6所示。

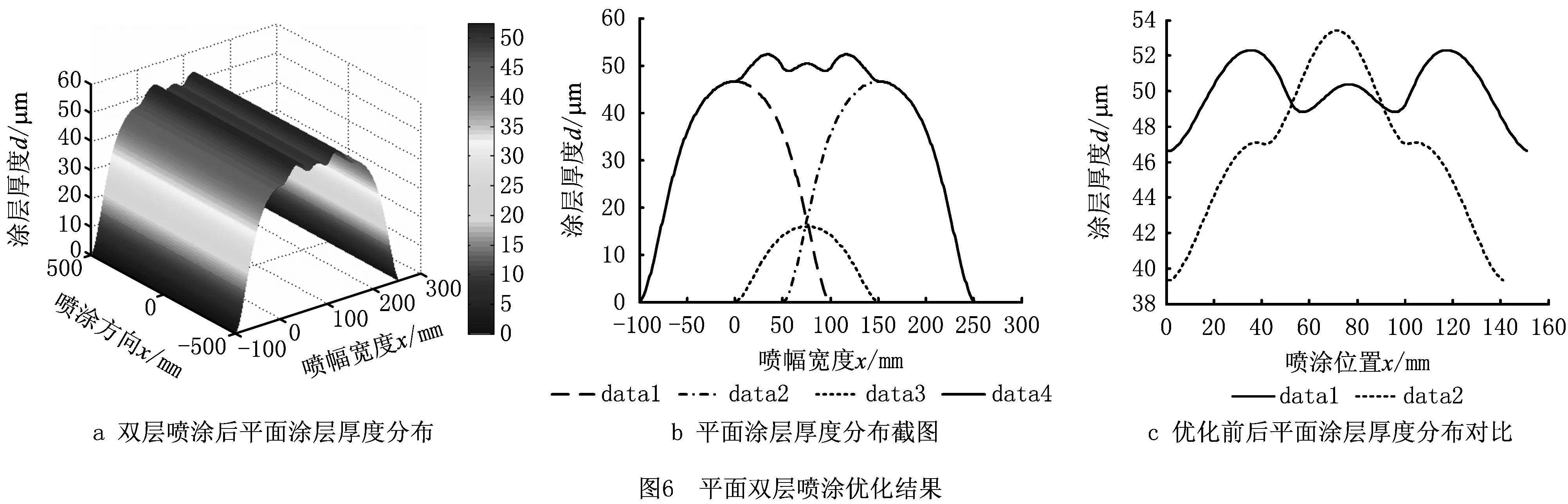
图6a为双层喷涂后平面涂层厚度分布图。图6b为图6a的截面图，其中：data1和data2分别为第1层喷涂相邻两道喷涂行程所形成的涂层厚度分布；data3是第2层喷涂所形成的涂层厚度分布；data4为双层喷涂后最终形成的涂层厚度分布。图6c为优化前后平面涂层厚度分布对比图，只选取了0～2a0-d1这一代表性区域作对比，其中，data1为优化后平面涂层厚度分布，data2为优化前平面涂层厚度分布。可以看出，优化后涂层厚度均匀性得到了明显提升。

同理，将第2层喷涂的涂层累积速率函数设置为0，得到目前常用的单层喷涂轨迹优化结果，算法在执行了179代后结束，得到最优解为[65.252，24.539]，即两道相邻轨迹重叠宽度d=65.252 mm，喷涂速度v=24.539 mm/s，此时涂层厚度分布如图7所示。

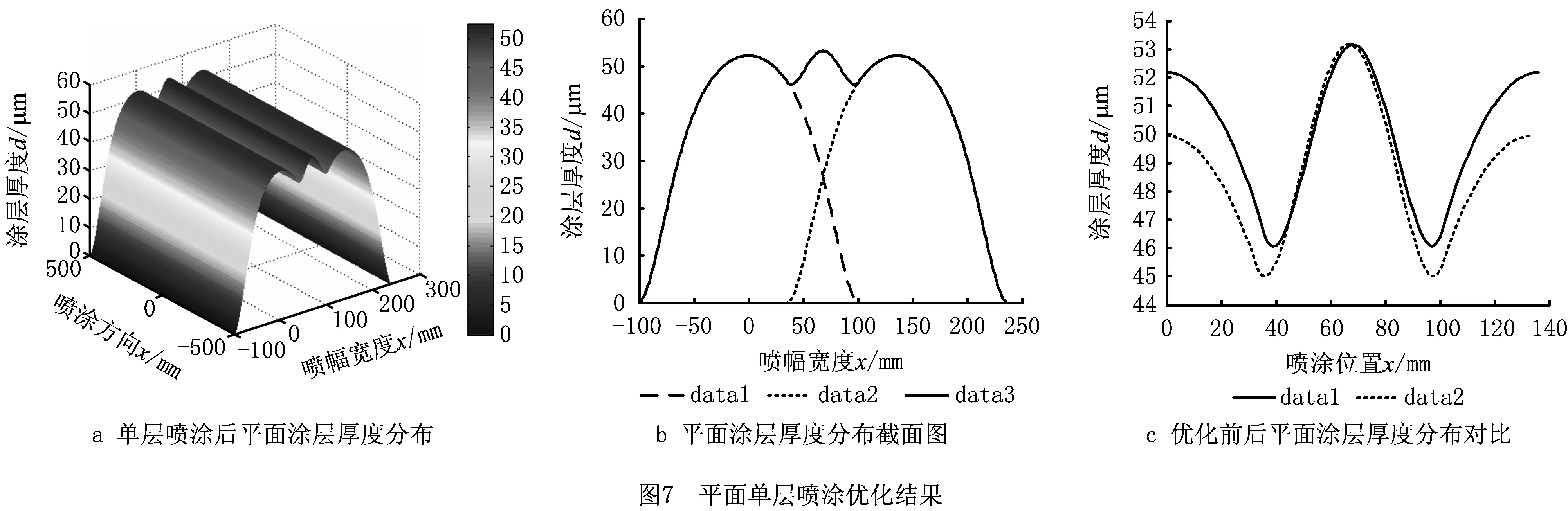
图7a为单层喷涂后平面涂层厚度分布图。图7b为图7a的截面图，其中：data1和data2分别为相邻两道喷涂行程形成的涂层厚度分布；data3为单层喷涂后最终形成的涂层厚度分布。图7c为优化前后平面涂层厚度分布对比图，只选取了0～2a0-d1这一代表性区域作对比，其中，data1为优化后平面涂层厚度分布，data2为优化前涂层厚度分布。可以看出，优化后涂层厚度均匀性得到了明显提升。

2.4 平面单、双层喷涂优化结果对比

如图8所示，data1曲线是单层喷涂优化结果，此时适应度值即喷涂后各点的涂层厚度值Di与理想涂层厚度值DA之间的方差为4.864 618，厚度最大值为53.16 um，厚度最小值为46.07 um，极差为7.092 um；data2曲线是双层喷涂优化结果，此时适应度值即喷涂后各点的涂层厚度值Di与理想涂层厚度值DA之间的方差为2.555 104，厚度最大值为52.31 um，厚度最小值为46.61 um，极差为5.7 um。

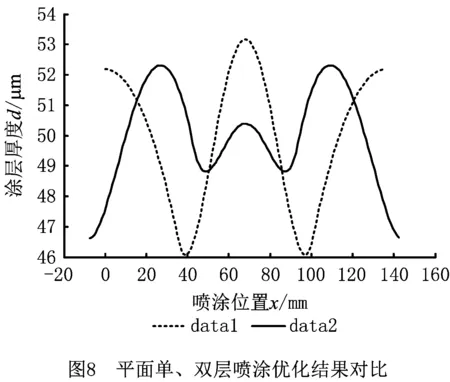
可以看出，相比于单层喷涂而言，平面双层喷涂所得涂层厚度最大值降低了0.85 um，最小值增大了0.54 um，极差降低了1.391 um，方差降低了2.309 514，提升效果较为明显。平面双层喷涂后所得到涂层厚度符合要求。

3 圆柱面双层喷涂自动轨迹规划

3.1 圆柱面涂层累积速率模型

由于不同工件表面造型各异，绝大多数工件表面并不只由平面构成，为了得到喷涂后工件表面涂层厚度分布，需要结合工件表面CAD模型，利用微分投影法，将立体涂层累积速率模型向工件表面映射，得到工件表面涂层累积速率模型，并在行对应喷涂时间上进行积分。以圆柱面为例，运用微分投影法将立体涂层累积速率模型映射到圆柱表面，得到圆柱面涂层累积速率模型。

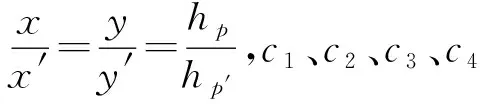
根据式(3)，结合P点与P′点的厚度及坐标关系，得出圆柱表面涂层累积速率模型为

(7)

式中：

x=-Rsinαp，

hp=hp′+R(1-cosαp)，

(8)

3.2 圆柱面双层喷涂后涂层厚度分布

圆柱面双层喷涂轨迹如图10所示，其中第1层为“Z”形轨迹，喷枪轴线与圆柱中心线垂直相交，任意两道相邻轨迹所对应的圆心角，即喷涂转角为η，喷涂距离为h0，喷涂速度为v1；第2层也为“Z”形轨迹，喷枪中心位于第1层喷涂两相邻轨迹中间位置，喷枪轴线与圆柱中心线垂直相交，喷涂距离为h2，喷涂速度为v2。对于圆柱面某点而言，共经历了3道喷涂行程，第1层有两道，喷涂转角为η，第2层有一道，位于第1层两道喷涂行程中间位置。可以看出，双层喷涂后，圆柱面上的涂层厚度分布由若干个涂层厚度分布完全相同的带状区域组成，带状区域宽度为η。可选取喷涂起始位置第一块带状区域进行规划，以减少计算量。

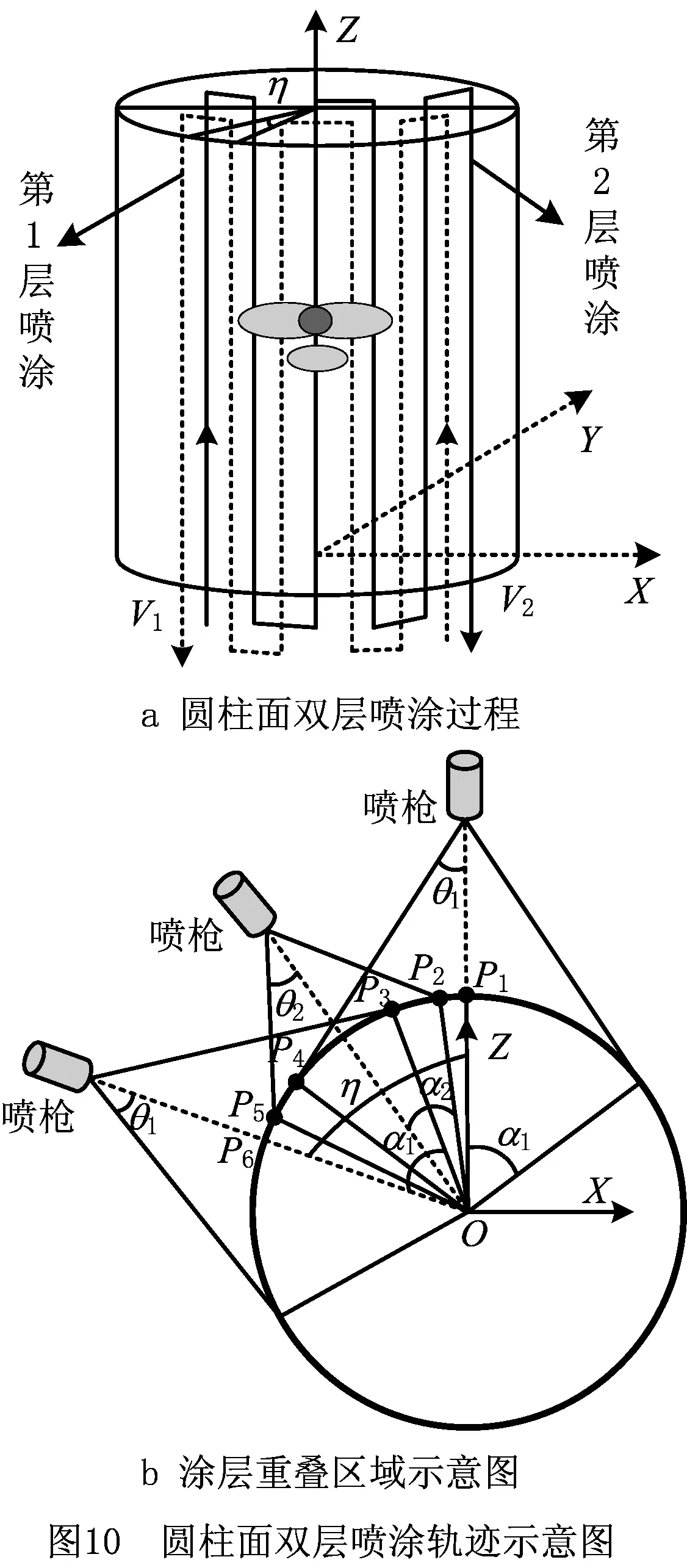
图10中：P1，P2，P3，P4，P5，P6所对应的αp值分别为0，η/2-α1，η-α1,α1，η/2+α2，η；η为喷涂转角；α1和α2分别为第1层和第2层喷涂区域极限位置所对应的最大圆心角。

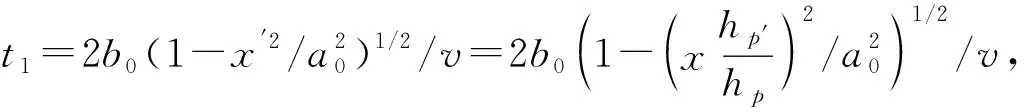
(9)

式中x,y,hp,θp与α,v的关系式如式(8)所示。

用D1a(α,v1)表示第1层第一道喷涂行程在表面P点形成的涂层厚度，则第1层第二道喷涂行程在表面P点形成的涂层厚度D1b(α,η,v1)可由D1a(α,v1)在偏转η得到；同理将式(7)中喷涂距离hp′的值由h0改为h2,喷涂速度v的值由v1变为v2，并在喷涂时间上积分，即可用D2(α,v2,h2)表示第2层的喷涂行程在P点形成的涂层厚度，得到圆柱面双层喷涂后表面点P的涂层厚度分布函数为

(10)

3.3 圆柱面双层喷涂轨迹优化目标函数

由式(10)可知，喷涂后得到均匀的涂层厚度的关键在于规划好合理的η、v1、h2和v2。相较于目前常用的单层喷涂，多引入了第2层喷涂的喷涂距离h2和喷涂速度v2两个优化变量。针对这一优化问题，在0～η之间，每隔0.002 rad选取一个点，n为总点数，以这些点的涂层厚度值Di与理想涂层厚度值DA之间的方差最小为优化目标建立优化函数：

(11)

结合喷涂经验及设备性能，对η、v1、h2和v2进行如下约束：η∈[0.208 7,0.417 4];v1∈[5,250];h2∈[150,300];v2∈[5,250]。

3.4 遗传算法求解及仿真

利用遗传算法对该优化问题进行求解，过程如下：

(1)涂层厚度分布模型参数选取 圆柱半径R=500 mm，喷涂距离h0=300 mm，a0=100.668 mm，b0=30.912 mm，Dmax0=39.8 um，β1=2.331，

β2=3.139，dA=50 um。

(2)遗传算法参数选取 适应度函数为式(11)，4个变量的取值范围下界为[0.208 7,5,150,5]，上界为[0.417 4,250,300,250]；种群规模为50，初始种群随机产生；适应度尺度变换为排序方式；选择方式为随机均匀分布；精英个数为4，交叉率为0.8；变异函数为高斯函数；交叉方式为多点交叉；迁移方向为前向，迁移率为0.2，迁移间隔为20；最大代数为800，适应度限为无穷小，停滞代数为50。

(3)优化结果 算法执行554代后结束，得到最优解为[0.257，25.427，184.700，176.364]，即第1层喷涂任意两道相邻轨迹喷涂转角η=0.257 rad，喷涂速度v1=25.427 mm/s；第2层喷涂距离h2=184.700 mm，喷涂速度v2=176.364 mm/s，此时涂层厚度分布如图11所示。

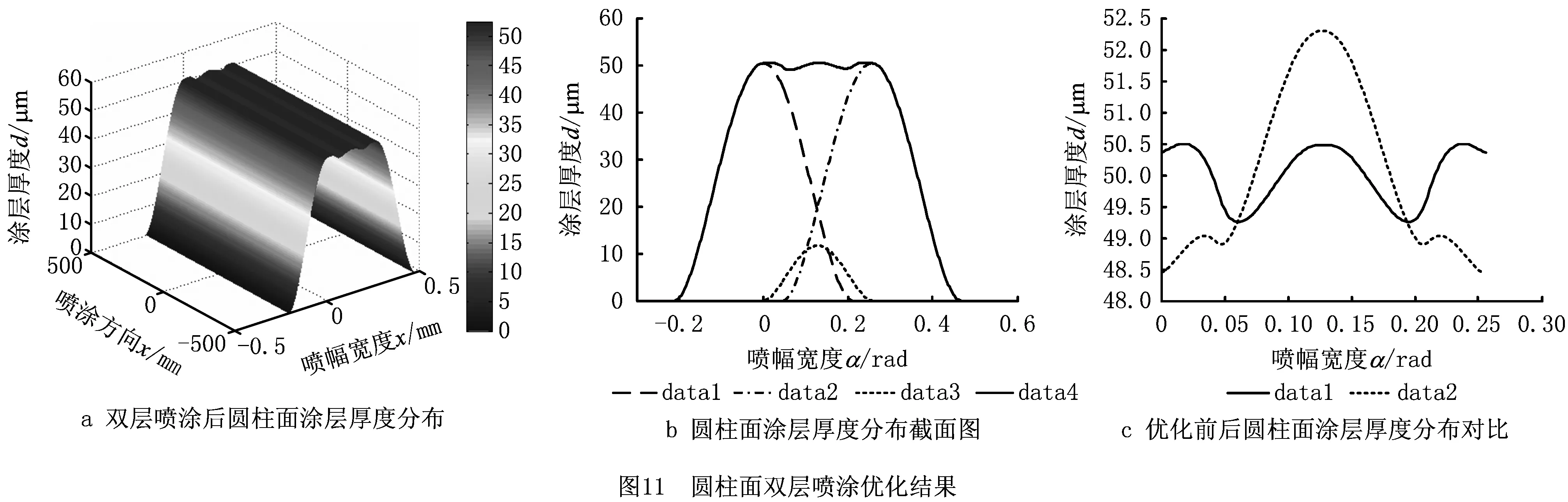
图11a为双层喷涂后圆柱面涂层厚度分布图。图11b为图11a的截面图，其中：data1和data2分别为第1层喷涂相邻两道喷涂行程所形成的涂层厚度分布；data3是第2层喷涂形成的涂层厚度分布；data4为双层喷涂后最终形成的涂层厚度分布。图11c为优化前后圆柱面涂层厚度分布对比图，只选取0～η这一代表性区域作对比，其中：data1为优化后圆柱面涂层厚度分布；data2为优化前圆柱面涂层厚度分布。可以看出，优化后涂层厚度均匀性得到了明显提升。

同理，将第2层喷涂的涂层累积速率函数设置为0，得到目前常用的单层喷涂轨迹优化结果，算法在执行252代后结束，得到最优解为[0.222，25.801]，即任意两道相邻轨迹喷涂转角为η=0.222 rad，喷涂速度v=25.801 mm/s，此时涂层厚度分布如图12所示。

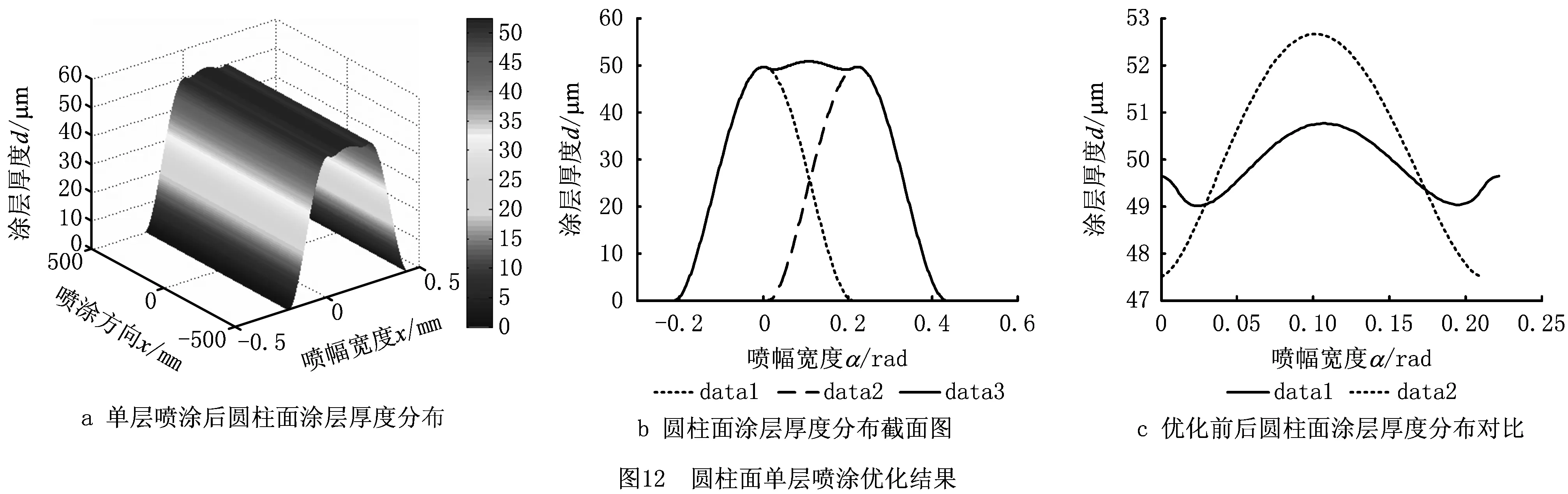
图12a为单层喷涂后圆柱面涂层厚度分布图。图12b为图12a的截面图，其中：data1和data2分别为相邻两道喷涂行程形成的涂层厚度分布；data3为单层喷涂后最终形成的涂层厚度分布。图12c为优化前后圆柱面涂层厚度分布对比图，只选取0～η这一代表性区域作对比，其中，data1为优化后平面涂层厚度分布，data2为优化前涂层厚度分布。可以看出，优化后涂层厚度均匀性得到了明显提升。

3.5 圆柱面单、双层喷涂优化结果对比

如图13所示，data1曲线是单层喷涂优化结果，此时适应度值即喷涂后各点的涂层厚度值Di与理想涂层厚度值DA之间的方差为0.402，厚度最大值为50.76 um，厚度最小值为49.01 um，极差为1.751 um；data2曲线是双层喷涂优化结果，此时适应度值即喷涂后各点的涂层厚度值Di与理想涂层厚度值DA之间的方差为0.248，厚度最大值为50.50 um，厚度最小值为49.25 um，极差为1.250 um。

可以看出，圆柱面双层喷涂相比于单层喷涂而言，所得涂层厚度最大值降低了0.26 um，最小值增大了0.24 um，极差降低了0.501 um，方差降低了0.154，提升效果较为明显。圆柱面双层喷涂后，涂层厚度均匀性符合要求。

4 喷涂实验结果分析

下面结合本文建立的立体涂层累积速率模型与双层喷涂自动轨迹规划方法进行喷涂实验。实验对象为某油箱，外表面主要由平面和圆柱面构成，尺寸为500×240×200 mm；理想涂层厚度为50 um，涂层厚度允许误差为5 um；采用课题组自主研发的六自由度喷涂机器人；重庆长江涂装设备有限责任公司生产的ZPQ9型喷枪，喷枪两端空气压力0.3 MPa；油漆选用干燥时间短的双组份丙烯酸漆工程机械用漆，涂料温度25 ℃，粘度(涂-4杯)18 s，涂料流量为0.15 L·min-1；在室温25 ℃，相对湿度50%条件下进行喷涂。喷涂过程中喷枪中心轴线始终垂直于油箱表面。油箱喷涂实验过程及喷涂效果如图14所示。

双层喷涂实验中，根据第2章和第3章的仿真结果，得到平面部分第1层喷涂任意两道相邻轨迹重叠宽度d1=50.382 mm，喷涂速度v1=27.474 mm/s；第2层喷涂距离h2=224.929 mm，喷涂速度v2=128.675 mm/s；圆柱面部分第1层喷涂任意两道相邻轨迹喷涂转角η=0.257 rad，喷涂速度v1=25.427 mm/s；第2层喷涂距离h2=184.700 mm，喷涂速度v2=176.364 mm/s。

单层喷涂实验中，根据第2章和第3章的仿真结果，得到平面部分任意两道相邻轨迹重叠宽度d=65.252 mm，喷涂速度v=24.539 mm/s；圆柱面部分任意两道相邻轨迹喷涂转角为η=0.222 rad，喷涂速度v=25.801 mm/s。

利用HS-GM200便携式涂层厚度测试仪，采用随机采样法采集喷涂后油箱表面平面和圆柱面部分20个点的涂层厚度数据。对每一个测量点，重复测量5次后取平均值作为最终结果。测量结果如表1所示，其中涂层厚度1为单层喷涂后的测量结果，单位为μm，涂层厚度2为双层喷涂后的测量结果，单位为μm。

表1 单、双层喷涂后测点涂层厚度表

如图15所示，data1为单层喷涂后测点涂层厚度折线图，data2为双层喷涂后测点涂层厚度折线图。实验结果显示，单层喷涂后测点厚度最大值为53.01 um，最小值为48.03 um，极差为4.98 um，均值为50.35 um；双层喷涂后测点厚度最大值为52.58 um，最小值为48.76 um，极差为3.82 um，均值为50.17 um。可以看出，相比于单层喷涂，双层喷涂在喷涂均匀性上有着较为明显的提升，且双层喷涂后测点最大误差的绝对值小于5 um，满足喷涂质量要求。

5 结束语

现代制造业中，越来越多的工件不仅要求涂层较厚，还要求严格控制涂层均匀性。在单层喷涂无法满足需求的情况下，本文提出一种基于遗传算法的双层喷涂自动轨迹规划方法，并将该方法应用于平面和圆柱面喷涂，取得了良好的效果。仿真及喷涂实验结果显示，双层喷涂后工件表面涂层厚度的最大值、最小值、极差及其与理想厚度值的方差，均有明显提升，所得涂层质量满足喷涂要求。在实际应用中，可通过采用喷涂机器人的流水线作业，以及不同工艺参数喷枪的组合使用，来进一步提高双层喷涂效率。后续可在双层喷涂自动轨迹规划基础上，在考虑喷涂机器人自身速度和位姿误差的条件下，开展多层喷涂自动轨迹规划的研究。