OFDM系统中的窄带干扰抑制

, ,

(1.中国电子科技集团公司 第五十四研究所，石家庄 050081;2.中国人民解放军第96764部队，河南 洛阳 471000)

0 引言

正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)由于其对多径衰落的鲁棒性和频谱效率的突出优势，已经成为一种重要方法[1]。许多无线通信系统，如数字音频广播(Digital audio broadcasting, BAD)、无线局域网(Wireless LAN, WLAN)和长期演进技术(long term evolution, LTE)等都采用了OFDM技术[2]。

在过去几年当中，无线服务的爆炸式增加导致了对频谱的需求持续增加。解决这一稀缺资源短缺的一个很有前景的方案是在几个独立的无线系统中使用相同的频率波段[3]。而这样做的弊端就是会造成不同独立的无线系统之间相互干扰，其中比较常见的一种干扰是窄带干扰(narrowband interference, NBI)。窄带干扰是对OFDM系统的有效干扰之一，它可以显著降低OFDM的误码率(Bit Error Rate,BER)性能。如图1所示，在不同的干扰信号比(interference-signal power rate,ISR)之下,系统误码率性能随着干扰信号比的提高而快速下降，在干扰过大的情况下系统甚至无法进行通信。

图1 窄带干扰对系统的影响

因此，针对OFDM系统中NBI的影响，以前已有一些研究。在有NBI影响的情况下，提高系统性能的方法可以简略地分成以下两类： 1)干扰最小化：不需要主动了解或利用与干扰相关的知识[4]；2)干扰消除：对干扰进行预测并且实现抵消[5]。

最早的干扰最小化方法是使用奈奎斯特(Nyquist)窗口，这个方法在[6]中得到了深入的探索，其中不同类型的Nyquist窗口是基于不同的信噪比最大化约束；另一种NBI最小化方法是[7]中开发的干扰抑制OFDM(IS-OFDM)。这种干扰最小化的方法不需要知道干扰信息，易于实现，但是效果不是很好。

干扰消除包括在时域或频域先验中估计干扰或其属性之一。频域干扰消除法主要是门限法，其中门限值的选定对干扰消除结果影响非常大，如果门限值设定过高，则会导致受NBI影响较小的子载波被漏检，如果门限值设定过低，则会将某些幅值较大的正常子载波当作受干扰的子载波造成误检，均会造成误码率性能降低。文献[8]中提出了一种抑制基于OFDM系统频谱泄漏的NBI抵消器，如果已知NBI信号的粗略先验信息则具有较为良好的性能。文献[9-10]探讨了基于滤波器的干扰消除方法，文献[9]中对NBI频率进行了估计并使用陷波滤波消除干扰。文献[10]中提出使用预测误差滤波器(Prediction error filter, PEF)来消除干扰，但是PEF指令必须足够长，否则有用信号将会严重受损。文献[10]提出了另一种干扰消除方法，利用最大似然(Maximum Likelihood, ML)估计法和频谱幅值信息估计频域干扰的相关参数，然后重建干扰并从接收到的信号当中消去干扰。该方法对干扰频率的估计精确度较低，对性能改善不大。并且在文献[10-11]中，都假设只有一个单音的NBI，然而在实践中NBI可能影响多个子载波。

本文描述了一个新型OFDM通信系统多音NBI抑制算法。首先尝试估计单个NBI信号，利用估计的参数重建单音NBI，随后在传输信号中消去它，接着用同样的方法移除下一个单音干扰，重复这个过程直到所有的干扰都被移除。这种方法造成的频谱泄漏非常小，并且尽可能的保留了有用信号。本文提出的算法基本保证了对NBI的准确估计，使系统的BER性能得到了非常大的提升。

本文其余部分如下所示：第一部分描述了系统模型；第二部分详细介绍了NBI抑制算法；第三部分给出了部分仿真结果图；最后第四部分总结全文。

1 系统模型

假设OFDM系统中没有符号间干扰(Intersymbol interference, ISI)和载波间干扰(Interchannel interference, ICI)，OFDM系统中的干扰只有高斯白噪声(Additive White Gaussian Noise, AWGN)和NBI。第n个采样期间接收到的时域信号由下式给出:

y(n)=x(n)*h(n)+i(n)+w(n)

(1)

其中:x(n),h(n),i(n),w(n)分别代表时域发射信号，信道冲击响应，NBI信号和AWGN，假设x(n),i(n),w(n)是相互独立的。

用单音干扰分量S来表示多音窄带干扰信号，则它的时域表达式为:

(2)

其中:T代表周期，Es,fs,θs分别是第s个单音NBI分量相应的功率，频率和相位。第s个干扰信号的频率定义为:

0≤λs≤N-1 -0.5≤αs≤0.5

(3)

(4)

此公式有两种不同干扰的情况，当αs=0时，干扰位于其中的某一个子载波上且与其正交。当αs≠0时干扰与任何子载波都不正交。

假设循环前缀(Cyclic prefix, CP)的长度Lcp大于信道时延扩展，经过去除CP和FFT之后的接收信号为:

Yk,l=Hk,lXk,l+Ik,l+Wk,l

k=0,1,…,N-1l=1,2,…,L

(5)

其中:Yk,l是接收到的信号，Hk,l是信道响应，Ik,l是窄带干扰而Wk,l是频域第l个OFDM符号的第k个子载波上的噪声，L是OFDM符号数量。时域上第l个OFDM符号的第n个子载波上的窄带干扰in,l和Ik,l的关系为:

(6)

将式(4)代入式(6)，得到Ik,l表达式如下[10]:

(7)

(8)

(9)

所以(8)可以改写为:

(10)

(11)

第k个子载波上的第s个干扰信号的功率为:

(12)

我们从式(12)中可以看出，当NBI与子载波正交(αs=0)时，第k个子载波上的干扰功率为:

(13)

在这种情况下，干扰只影响子载波λs。但是当干扰与子载波不正交时，干扰的能量就会泄漏到所有子载波上，而且当|αs|=0.5时能量泄漏最为严重。

为了反映第s个干扰分量对不同子载波的影响，图2展示了不同ISR时每个子载波上的干扰功率，其中干扰位置位于第200个子载波与第201个子载波之间。可以看出，当干扰与子载波不正交时，随着干扰功率的增加，会有更多的子载波被干扰影响。因此文献[11]中提出的方法是一个明智的选择，因为它考虑了整个频段的干扰，并有效地消除了频谱泄漏的影响。

图2 不同干扰信号比下子载波上的干扰功率

2 建议的NBI抑制算法

本文介绍的NBI抑制算法试图对频域中的NBI信号实现精确的估计和重建，再从接收信号中减去重建的NBI信号，从而完成NBI抑制。干扰消除的过程包括以下步骤：

1)通过提出的NBI估计算法来估计期望的多音干扰其中的一个干扰的参数(即频率，功率和初始相位)。

2)利用上一步骤中估计出的干扰参数来重建NBI，并在接收端将其减去以达到抑制NBI的目的。

3)计算子载波的平均功率并将其与阈值进行对比，如果其超过阈值，说明剩余仍然剩余干扰，那么就跳转到步骤1，否则的话结束整个过程。

重复以上过程，直到所有干扰都被取消。在本文中主要说明步骤1，即NBI参数的估计方法，其中的重点是NBI频率的估计算法。干扰估计算法被分为两部分，首先通过零填充插值的频谱搜索方案实现干扰频率大致估计。然后采用改进的加权相位平均(Weighted Phase Averaging,WPA)算法对干扰频率进行较为准确的估计。接下来，我们将以单音干扰为例子，分别将λ和α作为要大致估计和准确估计的干扰频率进行估计。

2.1 干扰频率大致估计

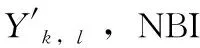
(14)

2.2 干扰频率准确估计

文献[13]中提出的WPA算法仅适用于单个复杂正弦信号的频率估计，无法很好地处理多个正弦信号，而且尽管加权相位平均法估计量计算效率较高，但是它存在严重的信噪比“门限效应”，此算法所求的单音信号频率为有用信号的频率，其能量远远大于信道噪声的能量，在信号能量比较小的情况下，此方法估计精度会大幅度下降。而本文需要求的单音信号频率为窄带干扰信号，相对于有用信号来说，窄带干扰信号的强度不一定总是远大于有用信号，当干扰较小的时候就会出现“门限效应”，造成干扰频率估计不准确。为了改善此算法的缺点，我们将加权相位平均算法应用于频域中的谱峰，因为在采用N点FFT之后，频谱峰值上的信噪比将增加N倍，所以信噪比“门限效应”将得到极大的改善。在本篇文章中，有用信号和背景噪声可以被近似地视为是干扰相位的一部分[13]。那么接收到的信号可以近似为:

(15)

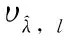
(16)

(17)

通过对式(17)应用WPA算法来获得较为准确的NBI频率估计，即:

(18)

(19)

NBI频率估计过程总结如下：

首先利用ML法结合零填充插值法得到大致的NBI频率估计；其次，将大致估计出来的NBI频率用于变换接收信号频率；最后应用改进的WPA算法来获得频域中的NBI频率的准确估计。

(20)

(21)

并且被从接收信号当中移除。在多音干扰中的一个被移除之后，以相同的方式继续估计并消除下一个干扰。重复整个过程，直到所有的NBI都被消除。整个过程总结如图3所示。

图3 算法的流程图

3 仿真结果及分析

本节介绍仿真结果验证本文提出的NBI消除算法在OFDM系统下的性能，并且将其与文献[13]中的算法进行对比。设置的仿真参数如下所示：OFDM调制使用循环前缀长度为1/4的256点FFT，数据子载波个数为223个，导频子载波个数为33个，梳状导频间隔设置为8，OFDM符号数为128，使用QPSK星座映射方式。为了专注于NBI所引起的错误而不是信道估计错误，我们假定信道估计是完美的，没有载波频率或者相位偏移，也没有样本定时偏移，NBI在信号通过信道的时候加入。其中BER是衡量系统性能的一个重要参数。

在实际应用当中，本文所提出的改进算法是通过在接收端计算接收子载波的平均功率，并将其与设置的阈值进行比较，如果子载波的平均功率大于阈值，那么就认为存在干扰，接下来需要对干扰参数进行估计。首先利用ML结合零填充插值法对干扰频率进行初步估计，再利用初步估计值变换接收信号的频率，最后应用改进的WPA算法来获得NBI频率的准确估计。然后根据邻近2P+1个子载波的平均值来估计干扰的其他参数，从而重构出NBI并进行抵消。直到处理后的接收子载波平均功率不高于阈值，即可视为NBI都被消除。

以下是不同的ISR情况下，系统误码率与信噪比的仿真结果图。分别模拟了无干扰时的情况、无干扰抑制时的情况、采用原有的算法以及采用本文提出的改进算法时的情况。如图4所示，是当α+λ=200.2，ISR=20 dB时，系统误码率随着信噪比的变化曲线图。在不进行干扰抑制时，系统的误码率很高，无法进行正常通信；采用文献[13]中的算法和本文所提的改进算法的系统中误码率曲线较为接近，并且与无干扰情况下的误码率差距不大，系统可以正常通信。

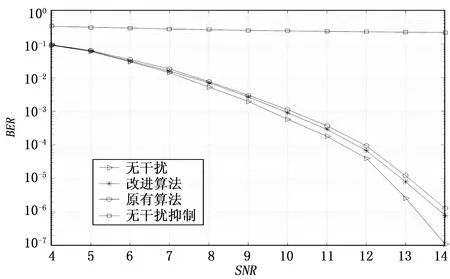
图4 干信比等于20 dB时信噪比与误码率曲线

如图5所示，是当α+λ=200.2，ISR=0 dB时，系统误码率随着信噪比的变化曲线图。在不进行干扰抑制时，系统的误码率比之前ISR=20 dB时要低，但仍不足以维持正常通信；采用文献[13]中的算法时，误码率性能与不进行干扰抑制时的性能相似，无法维持系统正常通信；而采用了本文所提的改进算法的仿真曲线因为ISR的降低，BER更加接近无干扰的情况，性能反而得到了提升。

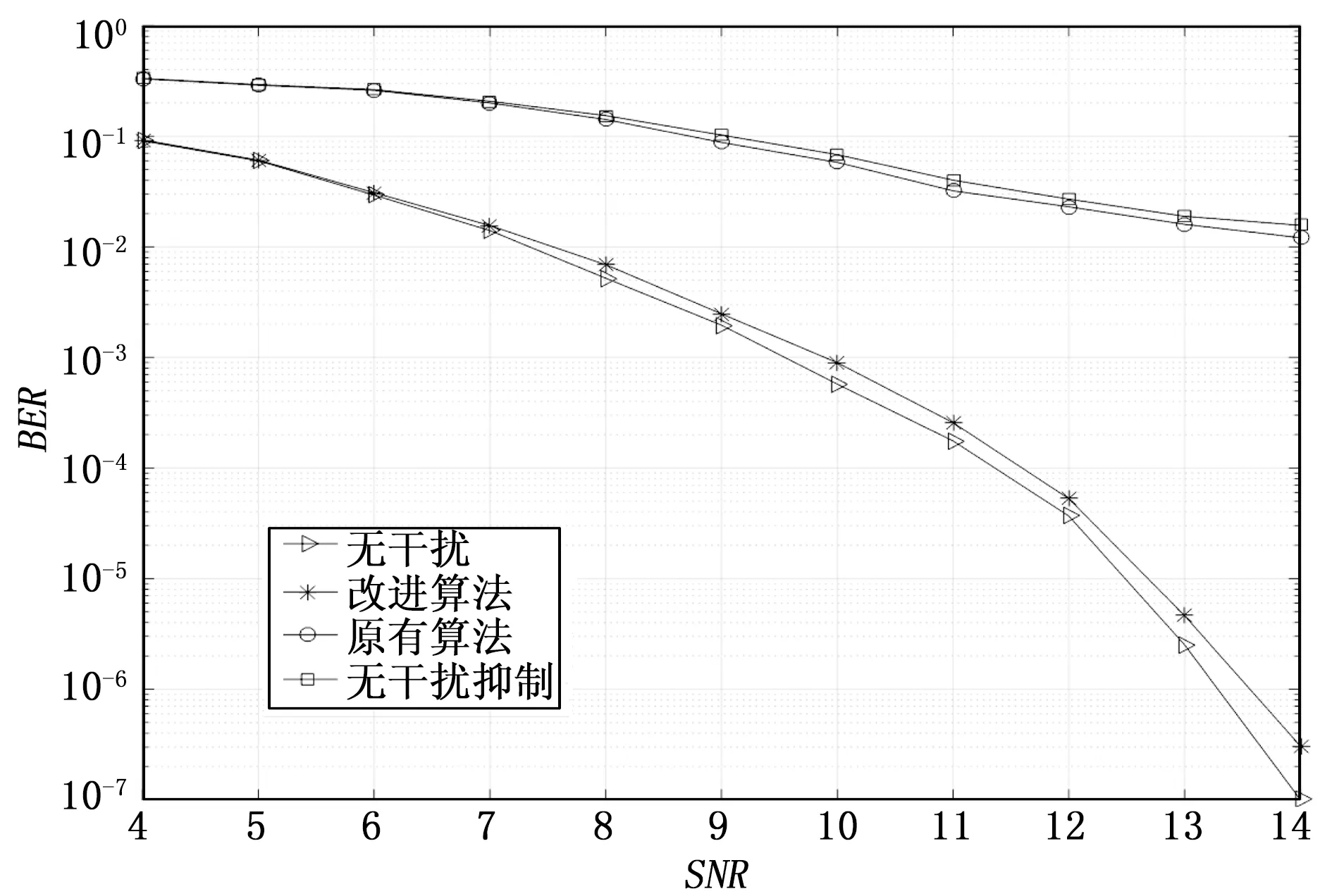
图5 干信比等于0 dB时信噪比与误码率曲线

由图4图5可以对比总结出，当系统受到窄带干扰影响时通信性能会严重下降，干扰功率越大，系统误码率越高。而算法性能会随着信噪比的增加而提升，信噪比越高，系统误码率越低。在不同的干信比情况下，本文提出的改进算法性能都很优秀，对系统性能提升有很大作用，而文献[13]中的方法只有在干扰较大的时候才对系统性能提升有明显作用，在干扰较小的情况下甚至与无干扰抑制时系统误码率相似。通过对比可以得出改进的干扰抑制算法适用性更广，在不同的干信比情况下都可以对系统性能有很大提升。

4 总结

本文针对OFDM系统中常见的NBI，提出了一种频域NBI估计和消除算法。通过估计、重构，最后从发送信号中消去多音NBI信号。上文已经详细说明了NBI的估计算法，通过利用ML法结合零填充插值法和改进的WPA算法来较为准确的估计NBI。在ISR超过0dB的情况下，算法精度非常高，并且在不降低有效信号的情况下显著降低了频谱泄露。经过计算机仿真表明其改善BER的性能优于其他抗干扰算法。