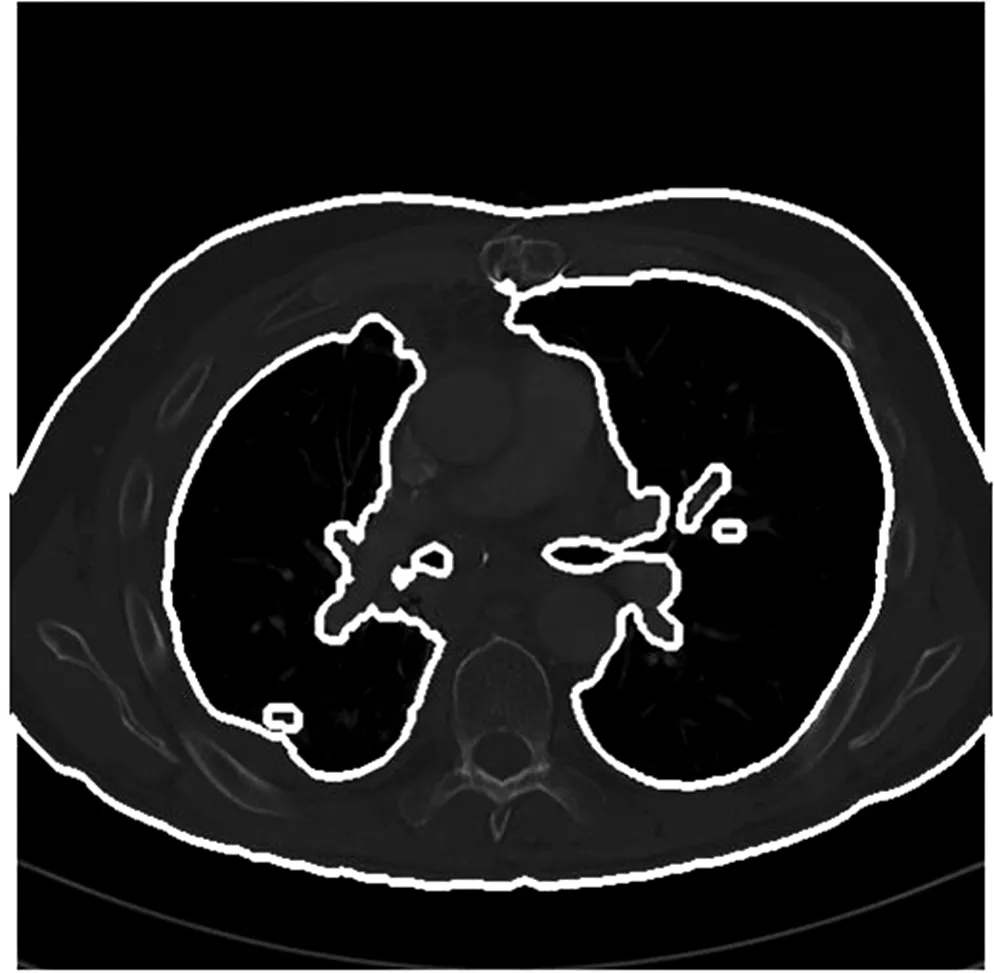
肺部ct的肺实质分割方法

(山西师范大学 山西 临汾 041000)

在传统动态曲线方法中。曲线运动过程中会出现多条曲线合并成一条，或一条分裂成多条的现象。这时拓扑结构发生了变化，无法用一条连续曲线的运动来表示轮廓的发展，在水平集中通过把上述曲线表示成一个连续变化的曲面与一个固定的平面的交线。此时可以表示拓扑结构变化。

水平集的分割过程是把图像中的轮廓看作某一个不断演化的二维函数的曲面与值为0的平面的交线。曲面按照它所满足的发展方程进行迭代，同时水平集函数也在演化，当交线演化趋于平稳时，演化停止，得到轮廓的形状。

假设分割轮廓由y=f(x)表示，隐函数表示为y-f(x)=0，此时若设：

φ(x,y)=y-f(x)

式(1)

则φ(x,y)=0就是曲线的隐式表达式。

对于φ(x,y)的构建，一般采用符号距离函数，即

式(2)

其中d[(x,y),C]是点(x,y)为曲线C的欧几里得距离。此函数即包含所求轮廓曲线。曲面的演化可分为两种类型，一种是基于图像边缘梯度信息的，一种是基于区域特征的。两种方式其实只是对曲面演化的速度方程的构建方式不同。即方程：

式(3)

中V(k)的构建。

水平集方法的基本流程：

1，初始化水平集函数φ(x,y)；

2，根据式(3)的演化方程演化曲线；

3，迭代一定的次数，提取0水平集，看是否已经收敛，如不收敛回到第一步。