岩体爆破裂隙区半径数值模拟参数分析

2018-10-17

福建质量管理 2018年18期

(华北科技学院河北廊坊 065201)

岩体爆破裂隙区半径数值模拟，即采用数值模拟软件对岩体爆破过程进行模拟，研究裂隙发育过程，并得到裂隙区半径，是岩体爆破裂隙区半径研究中很常用的方法[1-3]。一般采用实验获得岩石和炸药的材料参数，分析岩石强度理论，采用静态抗拉强度或动态抗拉强度，作为软件判断岩石单元失效的判据[4]，模拟所得半径即为岩体爆破裂隙区半径。很少有文章单独研究采用这种方法时，输入炸药不同参数对结果的影响。其次从岩石动态力学实验可知，岩石材料具有非常明显的应变率效应[5-7]，岩体爆破裂隙区半径数值模拟时考虑应变率效应和不考虑应变率效应，对裂隙区半径的影响值得研究。乳化炸药因长期存储将导致爆速和性能下降[8]，研究减小其爆速在模拟中可否体现炸药性能的下降。

一、3种典型炸药裂隙区半径数值模拟

选取三种具体代表性的炸药，C-4[9]、TNT[9]、乳化炸药[10]，分别建立岩体爆破裂隙区半径数值模拟模型，分析计算结果。

(一)计算模型

为提高计算的效率，对岩体爆破问题做以下简化：将模型考虑为深孔爆破，爆破介质假设为各向同性的均质弹塑性体。由于深孔爆破中，炮孔长度和直径比值，往往在100倍以上，因此可将岩体爆破过程当成准二维平面问题考虑。为定性分析深孔爆破裂隙区半径，建立如图1所示的有限元计算模型:模型尺寸为半径500cm；模型采用g-cm-μs单位制。爆破孔半径为5 cm，采用耦合装药结构。建模网格数量1.6万，炸药单元和岩石单元采用共节点的拉格朗日算法。

图1 有限元计算模型

(二)边界条件

本模型主要针对深孔爆破，因此不考虑边界应力波的反射作用，故计算模型的边界面添加透射边界特性，另外模型前后施加(Z轴)方向的约束。

(三)岩体状态方程参数

岩体选取LS-DYNA材料库中的弹塑性模型MAT_PLASTIC_KINEMATIC来代替，并添加MAT_ADD_EROSION关键字的方式来控制爆破过程中岩体的拉伸破坏。采用实验测得某种砂岩的材料参数，各项物理力学参数如表1所示。

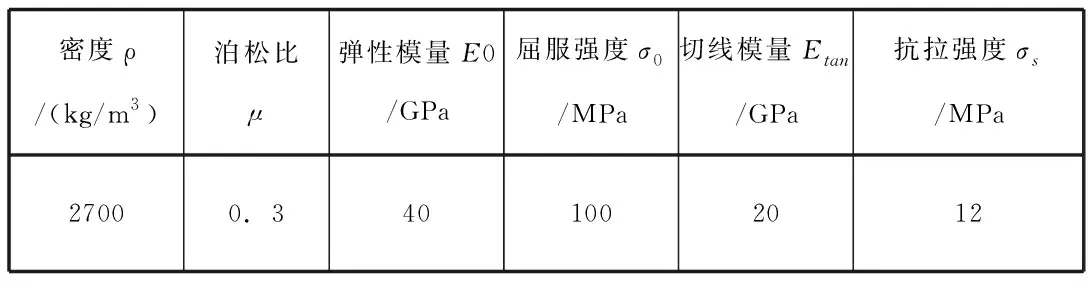
表1 岩石力学参数

(四)炸药状态方程参数

炸药选取LS-DYNA中的高能炸药模型MAT_HIGH_EXPLOSIVE_BURN，采用EOS_JWL状态方程描述炸药爆炸时的压力-体积膨胀关系。C-4[9]、TNT[9]、乳化炸药[10]三种炸药具体参数如表格2所示。

表2 炸药力学参数

(五)数值模拟结果及分析

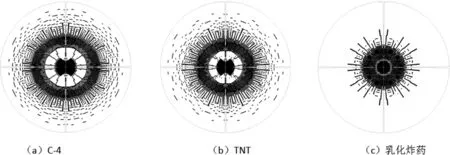
图2 t=1100μs时，不同炸药的裂纹扩展情况

由图2中模拟结果可知，不同炸药的爆破裂隙区情况有明显不同，在裂隙范围方面，C-4>TNT>乳化炸药，另外判定为失效的单元数量分别为4541、4381、3733。对于直接体现爆破损伤，C-4>TNT>乳化炸药。这与三种炸药的TNT当量大小所体现的爆炸损伤能力相吻合。说明该数值模型能够正确反应炸药性能强弱。二、应变率效应裂隙区半径数值模拟炸药爆破时近区岩体发生屈服，应变率效应明显。因此建立两个模型，分别为考虑应变率效应模型和不考虑应变率效应的模型，分析数值模拟结果。

(1)计算模型与边界条件

计算模型的几何结构、单元划分、以及边界条件与前文中的裂隙区半径数值模拟一致，不再赘述。

(2)岩体状态方程参数

岩体同样选取LS-DYNA中的弹塑性模型MAT_PLASTIC_KINEMATIC来代替，并添加MAT_ADD_EROSION关键字的方式来控制爆破过程中岩体的拉伸破坏。爆炸载荷时岩体的应变率效应明显。因此数值模拟中常采用在屈服应力中引入应变率因子的办法来模拟岩体在爆炸载荷下的性质。岩石屈服应力与应变率的关系如下：

(1)

(2)

因此分别建立添加C、P参数的考虑应变率效应岩石材料模型和不添加C、P参数的不考虑应变率效应的岩石材料模型。

岩体其他物理力学参数如表1所示。

(3)炸药状态方程参数

炸药选取LS-DYNA中的高能炸药模型MAT_HIGH_EXPLOSIVE_BURN，采用EOS_JWL状态方程描述炸药爆炸时的压力-体积膨胀关系。采用TNT[9]炸药进行模拟，具体参数如表格3所示。

表3 炸药力学参数

(4)数值模拟结果及分析

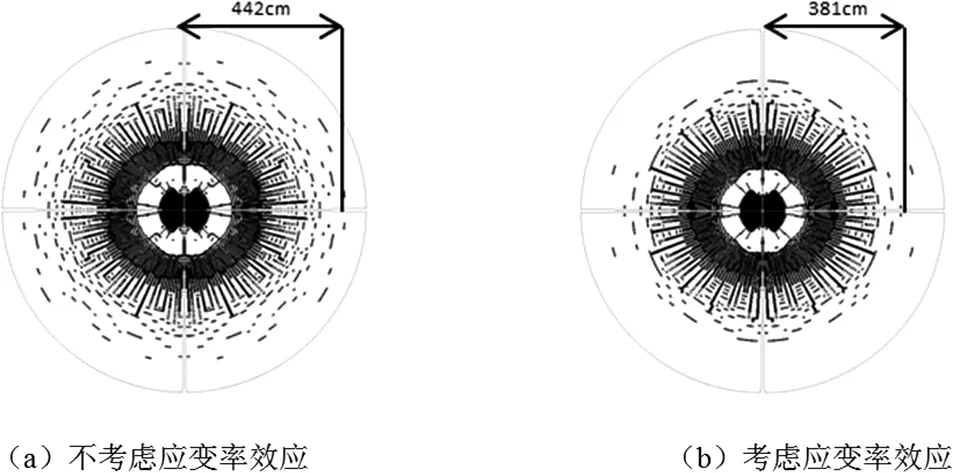
图3 t=1100μs时，不考虑应变率与考虑应变率裂纹扩展情况

由图3中模拟结果可知，不考虑应变率效应与考虑因变率效应模型，失效单元数量分别为4381和4326，二者差异不明显。但失效单元的分布明显不同，不考虑应变率效应的模型失效单元更分散，范围更广，裂隙区半径为442cm；考虑应变率效应的模型失效单元的比较集中，范围较小，裂隙区半径为381cm。对比可知，裂隙区半径减小了13%。从数值模拟理论分析可知，当考虑应变率效应时，由公式(1)可知近爆区屈服应力值更高，因此存储的弹性应变能相对提高，因此当弹性能释放时能够产生更大的拉应力，这一点与岩体在爆破载荷下的情况相符。所以采用抗拉强度作为单元失效判据时，失效单元就更容易集中于近爆区，导致爆破裂隙区范围较小。所以进行岩体爆破裂隙区模拟时，选用考虑应变率效应的岩石材料模型，能得到更符合实际情况的模拟结果。

三、乳化炸药爆速下降数值模拟

煤矿常用的乳化炸药在长期存放过程中，炸药性能会发生改变，最明显的是爆速下降。由于条件有限，无法获得炸药性能改变后的炸药状态方程参数，因此仅改变其爆速，模拟乳化炸药由于长期存放而导致的性能下降对爆破裂隙区半径的影响。

(一)计算模型与边界条件

该计算模型的几何结构、单元划分、以及边界条件仍与前文中的爆破裂隙区模型一致，不再赘述。

(二)岩体状态方程参数

岩体选取LS-DYNA材料库中的弹塑性模型MAT_PLASTIC_KINEMATIC，并添加MAT_ADD_EROSION关键字的方式来控制爆破过程中岩体的拉伸破坏。各项物理力学参数如表1所示。

(三)炸药状态方程参数

炸药选取LS-DYNA中的高能炸药模型MAT_HIGH_EXPLOSIVE_BURN，采用EOS_JWL状态方程描述炸药爆炸时的压力-体积膨胀关系。乳化炸药[10]具体参数如表4所示。

表4 炸药力学参数

(四)数值模拟结果及分析

图4 t=1100μs时，不同爆速下裂纹扩展情况

由图4中模拟结果可知，对爆速5166m/s、3700m/s、3200 m/s模型来说，随着爆速的减少，径向失效单元长度和数量也随之减少，长度275cm以上裂纹数量，按四分之一圆计算分别为5条，3条，2条。即爆速减小到3700m/s和3200m/s时，长度超275cm的径向裂纹分别减小了40%，60%。以上说明裂隙区半径随爆速变小而变小，这一点和乳化炸药存放时间长，爆炸性能有所下降的情况相吻合。这说明改变乳化炸药的爆速确实能够反应出乳化炸药由于长期存放导致的炸药性能下降。但是三者失效单元数量分别为3733、3759、3782，呈递增趋势，这与实际情况不符。这是因为JWL状态方程是反应炸药做功能力的，当乳化炸药性能下降时，JWL方程参数也随之改变。而本研究受条件限制，无法测得乳化炸药长期存放后JWL状态方程参数。如果能够获得相应参数模拟结果会更加符合实际。