肋片结构的冲击强化换热特性研究
2018-10-17曾文明谭晓茗
曾文明,谭晓茗,单 勇
(南京航空航天大学 能源与动力学院 江苏省航空动力系统重点实验室, 南京 210016)
射流冲击由于冲击流程短且被冷却表面流动边界层薄,是一种极其有效的强化局部传热或传质的方法[1-3],在航空航天、机械加工、电子器件冷却等方面应用广泛[4-6],也取得了丰富的研究成果。Farhana等[7]对二维湍流双斜缝射流进行研究,表明射流孔小于90°时,Nu由冲击面处向周围逐渐减小和平均Nu能更好地反映雷诺数大小,而冲击角度对冲击靶板间距反应不灵敏。关涛等[8]研究了射流孔交错偏置排布下的楔形凹腔表面对流换热,结果表明:射流交错孔偏置排布使得冲击驻点区对流换热增强,射流孔交错偏距比宜选着在1倍射流孔直径左右。Chaudhari等[9-10]研究了孔板参数对冲击换热的影响,发现孔板厚度与孔径是腔内对流换热的重要影响参数。
对于高性能燃气轮机高热负荷部件的冷却来说,单一射流冲击的冷却方式由于冷却能力的限制已难以满足需求,“冲击-肋片”的复合冷却具有结构简单、加工方便等优点,已成为燃气轮机涡轮叶片内部通道冷却的主要方式。
国内外研究人员对“冲击-肋片”复合式的强化换热开展了相关研究。Qiu等[11]对带肋结构的射流冲击换热特性进行研究,结果表明:带肋靶面射流冲击换热性能明显高于单一射流冲击。徐亚威等[12]对肋化平板射流冲击换热特性进行了实验研究,结果表明:间断肋片形式比连续的肋片形式有更好的强化换热效果,且冲击间距为射流孔径2倍时换热效果较好。Tan等[13]对半封闭通道内肋壁面射流冲击换热进行了实验研究,结果表明:肋壁区对流换热提高了30%,倒V形肋更有利于对流换热。谭蕾等[14]对半封闭肋化通道单排孔射流冲击进行研究,结果表明:冲击间距对肋化部分换热影响较大,V型肋化通道可获得最佳换热效果。Li等[15]对在射流孔倾斜阵列排布时低冲击间距进行了实验研究,结果表明:在低冲击间距下Nu沿流动方向逐渐减小且倾斜射流冲击Nu与常规射流冲击Nu相似。
本文基于某型涡轮导向叶片弦中心区冷却,构建“冲击-肋片”复合冷却模式。考虑到涡轮叶片弦中心区弧度较小,故简化成平直通道进行研究,主要分析冲击射流与肋片的相对排布、射流冲击雷诺数(Re)、肋片结构等参数对涡轮叶片表面对流换热的影响。
1 物理模型和计算方法
1.1 物理模型
本文以“冲击-肋片”的肋化通道作为研究对象,其结构如图1所示,由射流孔和带肋的冲击靶板组成。冷却气体从射流板上不同布置圆孔喷出后冲击到靶板表面,并经两侧排出。射流孔径通道高H=4 mm、y方向每单元周期宽W/H=4以及L/H=16;冲击孔直径d=2 mm,孔横向间距比P/d分别取2、2.65、4,排布方式如图2所示,其中冲击孔错排时在保证射流冲击孔开孔率不变,同时改变p和s为长菱形和正菱形。通道内的肋片等距排布,肋片形状分别是方形肋、梯形肋和三角肋(h为肋高,e为肋宽,h=e=1 mm),肋间距P1/h=8。
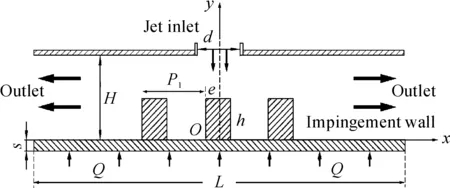
图1 冲击-肋片复合冷却示意图

图2 孔排结构示意图
鉴于物理模型的周期性结构特征,计算域在y向的两个端壁可以处理为周期性边界,在计算过程中,相应的边界条件和物性参数选着如下:
进口边界条件:给定射流管进口的进口质量流量,所对应的射流雷诺数(Re)分别为6 000、14 000、22 000和30 000;湍流度设定为5%且水力直径为射流孔孔径d;气流温度为300 K。
出口边界条件:设定出口为压力出口,出口大气压为101 325 Pa。
冲击靶板和肋边界条件:采用无滑移壁面边界条件,壁面和肋设定为恒定热流,热流密度为5 000 W/m2。
1.2 计算方法
采用ICEM对计算模型进行网格划分。图3所示为肋和射流孔网格划分。为了准确模拟射流冲击,在射流孔、肋壁面处采用附面层局部加密使得y+<5。为了验证网格的独立性,本文设计了4套网格,网格数分别为120万、160万、200万和240万,其差异主要是射流孔网格加密区及壁面和肋片近壁区加密所致。网格实验结果表明:当网格数为200万时,射流孔处温度、速度以及靶面、肋片的温度和换热系数分别不再随着网格量的增加而变化。

图3 肋和射流孔网格划分
利用Fluent软件,采用剪切应力输运SSTk-ω湍流模型,压力场求解采用SIMPLEC算法进行压力-速度耦合求解,离散方程均采用二阶迎风差分格式进行计算,收敛精度为10-5,残差趋势趋于平直且监测面的温度变化不大。
1.3 模型验证
湍流模型验证取自文献[6],射流雷诺数Re=10 000,H/d=2.0,L/d=41.7,W/d=10.42,射流孔直径d=6 mm。得到x方向上壁面Nu的分布,Nu的计算式为
(2)
式中Dh、Tw、Tin分别是入口的水力直径、壁面温度和进气温度。
图4为平板表面沿着x方向上展向平均努塞尔数(Nu)计算值,与文献[6]的对比得出,运用SSTk-ω模型计算结果与文献中实验数据吻合较好,计算值与实验值相差约在8%以内,其他对比相差均大于13.7%。而且文献[3]运用SSTk-ω模型,较好地预测了靶板的换热特性。

图4 计算结果的模型验证
2 计算结果与分析
2.1 肋片形状的影响
选择通道尺寸D/H=4,射流雷诺数Re=30 000,射流孔呈长菱形排布,研究光滑平板和肋片形状分别为方形、梯形和三角形的流动换热特性。图5为y=0(横截射流孔中心)截面上局部流场。可以看出:当射流孔长菱形排布时,射流冲击直接冲击到靶板上,在肋片周围形成较明显的涡流且肋为方形肋时较梯形肋和三角肋涡量尺度大,通道内部两侧的流动不对称。涡流的形成主要是由于肋的存在,随着肋结构改变,通道内涡流相对也随之改变。可以从图5中看出:为三角肋时,通道内涡流尺寸最大。涡量尺度增加主要是出现在肋片附近,在近壁处的气流流动受阻导致相应肋片处形成相对较大的角涡区。这一流动差异带来的换热影响如图6所示。
图6为不同肋结构和光滑表面时靶板表面Nu的分布云图。可以看出:在开孔率不变、射流孔为长菱形排布时,靶板和肋表面上射流冲击驻点区Nu较高,此外由于横流效应使得对流换热最弱的局部区域位于肋两侧;肋片结构为三角形布置方式时,其对于靶面冲击换热面积较大且相对均匀,即不会出肋结构为方形时对流换热出现最强局部区域的情况。从图中还可以看出:三角形肋的射流冲击靶面的对流换热最均匀;其次是梯形肋和方形肋,最后是光滑靶面。这主要是由于射流冲击到靶板上时,三角肋受到流阻要小于梯形肋和方形肋,使得冲击靶板上对流换热最均匀,而射流冲击到光滑靶板表面时驻点区Nu最大并沿着驻点向四周逐渐减小。此外,在横流作用下y方向上换热面积不均匀且存在较弱的局部对流换热区域,如图6(d)所示。

图6 带肋结构和光滑靶板表面对流换热影响
图7显示在通道尺寸W/H=4、射流雷诺数Re=30 000时,不同肋结构对展向平均Nu分布的影响。这里,沿展向平均Nu定义为
(3)
式中Nu(s,x)为冲击靶面的局部努塞尔数。
从图7可以看到在射流雷诺数Re=30 000时3种不同排布下的射流孔对冲击靶板展向Nuave,s分布的影响。不管射流孔如何排布,冷气流直接冲击靶板处的Nuave,s都存在峰值。注意到在肋结构为三角形对靶板表面对流换热相对均匀,最重要是在通道两端的对流换热更强。三角肋通道对应的冲击靶板上Nuave,s比梯形肋和光滑板面分别提高了7.1%和7.8%;梯形肋通道比方形肋通道上的Nuave,s提高了4.9%。

图7 不同肋结构通道和光滑靶板上展向Nuave,s分布
2.2 射流孔排布的影响
选择三角形肋片结构通道,射流雷诺数Re=30 000,在射流孔开孔率不变时分析射流孔排布方式对通道内对流换热的影响。图8为靶板表面展向Nuave,s的分布云图。可以看出,射流孔排布为长菱形布置方式时,靶板表面展向Nuave,s分布比顺排、正菱形布置方式更均匀,不存在局部对流换热强和局部对流换热弱的情况,同时由于肋存在对靶板内部通道涡流诱导也起一定作用。

图8 不同排布射流孔对靶板表面对流换热的影响
图9为不同冲击孔排布下冲击靶板展向Nuave,s分布。其中冲击孔为长菱形和顺排排布时,射流冲击下的靶板展向Nuave,s较冲击孔为正菱形排布的对流换热高。原因在于射流孔为正菱形较其他孔排时孔间距减小,并且靶板上局部对流换热更高,主要出现在驻点区。此外,孔为长菱形排布时靶板上驻点区对流换热相对均匀,不会出现孔为顺排时波峰与波谷处展向Nuave,s相差较大的情况。如图9所示,驻点区对流换热更高。射流孔为长菱形排布时靶板表面展向Nuave,s比顺排排布和正菱形排布相对应分别提高了10%和26.9%。

图9 不同冲击孔排布下冲击靶板展向Nuave,s分布
2.3 射流冲击雷诺数的影响
选择三角形肋结构通道,射流孔为长菱形排布,分析射流雷诺数对靶板表面对流换热的影响,结果如图10所示,从图中可以看出:射流冲击驻点区对流换热较大,随着雷诺数的增加,射流冲击靶板上展向Nuave,s越大,且主要集中在射流冲击驻点区,可能是由于肋的存在使得射流间距缩小导致射流冲击靶板上对流换热系数局部较大。此外,肋片结构为三角形时,射流冲击靶板上对流换热均匀,换热效果最好。
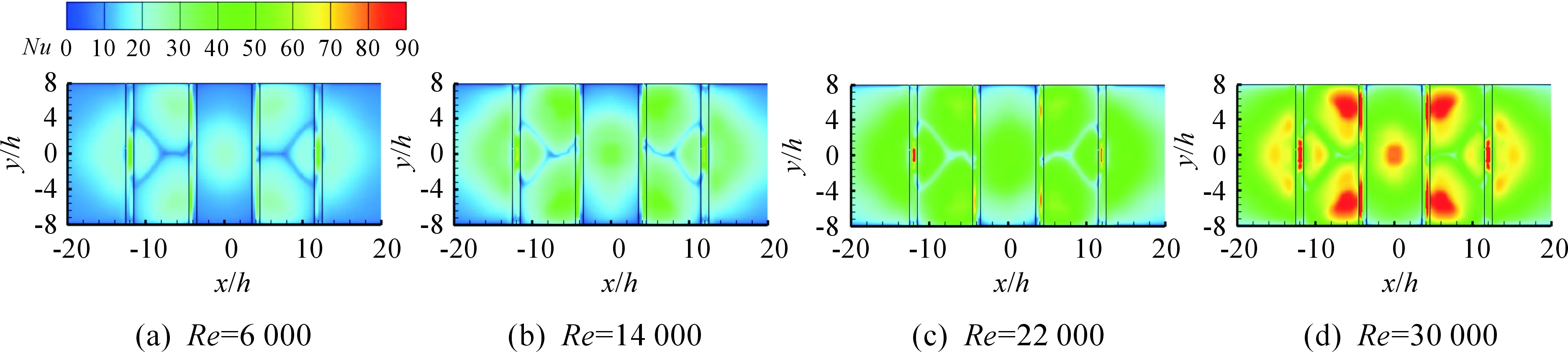
图10 射流雷诺数对靶板表面对流换热的影响
图11为不同射流雷诺数Re(6 000~30 000)下靶板展向Nuave,s分布影响。从图中可以看出:随着射流雷诺数Re增加,冲击靶面上对流换热不断增加。其原因在于,射流孔到靶板法向间距不变,增加射流雷诺数的大小,有利于提高冲击驻点区的局部表面传热系数。注意到冲击驻点区对流换热能力最强对应于图中波峰区域。此外,由于横流效应和肋片存在,出现局部最弱的对流换热区域,如图中波谷区域。在肋结构为三角形、射流孔为长菱形排布时,射流雷诺数Re=30 000较其他射流雷诺数Re(6 000、14 000和22 000)对靶板表面展向平均努塞尔数(Nuave,s)分别增加了31.12%、51.43%和70.57%。

图11 不同Re对靶板展向展向Nuave,s分布影响
为了在保持冲击靶板上对流换热能力不受到明显削弱的前提下,改善冲击靶板上射流冲击对流换热能力,射流冲击孔排布宜选择长菱形布置,且肋片结构选择三角肋,可以明显改善冲击靶板的对流换热能力。
3 结论
1) 当射流孔长菱形排布时,在肋片周围形成较明显的涡流,且肋为方形肋时较梯形肋和三角肋涡量尺度大,通道内部两侧的流动不对称;涡流的形成主要是由于肋的存在,随着肋结构改变,通道内涡流相对也随之改变;在近壁处的气流流动受阻导致在相应肋片处形成相对较大的角涡区。
2) 在开孔率不变、射流孔为长菱形排布时,靶板表面上射流冲击驻点区Nu较高。由于横流效应使得对流换热最弱的局部区域位于肋两侧。此外,靶面上冲击换热面积较大且相对均匀,即不会出现局部区域内对流换热最差的情况。当射流孔为正菱形布置,射流冲击驻点区Nu较长菱形布置时大,但对于靶面射流冲击换热不均匀。此外,肋片结构宜采用三角肋,当射流直接冲击靶板上时由于流阻减弱其对流换热更均匀。
3) 在本文所研究“冲击-肋片”复合冷却,为了在保持冲击靶板上对流换热能力不受到明显削弱的前提下改善冲击靶板上射流冲击对流换热能力,射流冲击孔排布宜选择长菱形排布,且肋结构选择三角肋,可以明显改善冲击靶板的对流换热能力。
