耦合非线性Schrödinger方程初边值问题整体解的适定性

陈渝芝，张晓强, 金世刚

(重庆理工大学 理学院， 重庆 400054)

1 Introduction

The coupled nonlinear Schrodinger equations:

(SE)

were proposed by [3] to describe the two-wave interaction through cubic nonlinear optical media(see also [2,4]). LetΩbe a domain inR2with compactly smooth boundaryΓ. We consider the following initial-boudary value problem:

(1.1)

(1.2)

u(t,x)=0,v(t,x)=0 (t,x)∈[0,∞)×Γ

(1.3)

u(0,x)=u0(x),v(0,x)=v0(x),x∈Ω

(1.4)

whereu(t,x) andv(t,x) are complex valued functions denoting the complex amplitudes of two interacting waves in nonlinear optical media,respectively.

Problem (1.1)-(1.4) whenΩ=R2has been studied in[2-5],but to our best knowledge,there is no any result whenΩ≠R2. In the present paper, we study the existence and uniqueness of global solution to the initial-boundary value problem (1.1)-(1.4). The main result of this paper reads as follows.

(1.5)

Δφ-φ+φ3=0

(1.6)

Then there exists a unique solution (u,v) for the problem (1.1)-(1.4) such that

(u,v)∈[C([0,∞);H2(Ω))∩C1([0,∞);L2(Ω))]×

[C([0,∞);H2(Ω))∩C1([0,∞);L2(Ω))]

2 Preliminaries

In this section, we give some preliminaries which are key to the proof of Theorem 1.1. In what follows we denote byCvarious constants depending only onΩ.

Firstly, the following result holds from Lemma 2 in[1]

Lemma2.1For (u,v)∈H2(Ω)×H2(Ω) with ||u||H1(Ω)+||v||H1(Ω)≤1, we have

(2.1)

Lemma2.2For (u,v)∈H2(Ω)×H2(Ω), we have

(2.2)

(2.3)

(2.4)

(2.5)

ProofFor (u,v)∈H2(Ω)×H2(Ω),letDdenote any first order differential operator, we have

(2.6)

which implies that

(2.7)

On the other hand,by Gagliardo-Nirenberg inquality,one has

(2.8)

(2.7) and (2.8) yield the estimante (2.2).

We next prove the estimate (2.3).By a direct calculation, we have

(2.9)

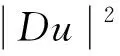
(2.10)

Combining (2.9) with (2.10) yields that

(2.11)

Thus, (2.3) follows from (2.11).

Similarly,we can obtain the estimates (2.4) and (2.5).

At the end of this section, we give the following result which is similar to Theorem 1 in Segal [6].

Lemma2.3Assume thatHis a Hibert space andAi:D(Ai)⊂H→His an m-acctrtive linear operator,wherei=1,2. LetFi(i=1,2) be a mapping fromD(A1)×D(A2) into itself which is Lipschitz on every bounded set ofD(A1)×D(A2).Then for any (u0,v0)∈D(A1)×D(A2),there exists a unique solution (u,v) of the Cauchy problem

(2.12)

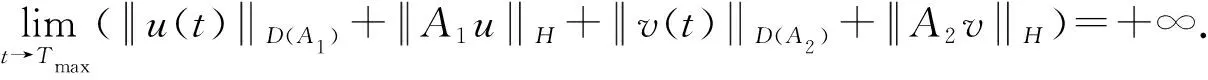
3 Proof of Theorem 1.1

In this section,we prove Theorem 1.1.We first give a lemma which concerns the conservation laws of the energy and of the mass by a direct calculation.

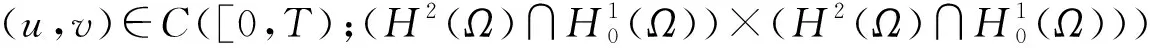
||u(t)||L2(Ω)=||u0||L2(Ω), ||v(t)||L2(Ω)=||v0||L2(Ω)

(3.1)

E(u(t),v(t))=E(u0,v0)

(3.2)

where

(3.3)

We now return to show Theorem 1.1

ProofofTheorem1.1Using Lemma 2.3, we let

(3.4)

We divide the proof into two steps.

Step1In this step, we show that ||u(t)||H1(Ω)and ||v(t)||H1(Ω)remain bounded fort>0.

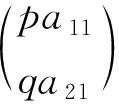
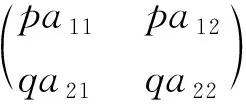
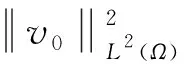
(3.5)

Applying Gagliardo-Nirenberg inequality

(3.6)

whereφis the ground state solution of (1.6), noting that (3.1), we have

(3.7)

Combining (3.5) with (3.7) yields that

||u(t)||H1(Ω)+||v(t)||H1(Ω)≤C

whereCis independent oft.

Step2In this step, we istablish that boundedness of ||u(t)||H2(Ω)and ||v(t)||H2(Ω).

LetSu(t) be theL2isometry group generated byA1,Sv(t) be theL2isometry group generated byA2. By (1.1) and (1.2), we have

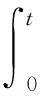
(3.8)

(3.9)

and

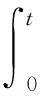
(3.10)

(3.11)

Thus one has

(3.12)

(3.13)

It follows from Lemma 2.2 that

(||u(s)||H2(Ω)+||v(s)||H2(Ω))≤C(||u(s)||L∞(Ω)+||v(s)||L∞(Ω))2·

(||u(s)||H2(Ω)+||v(s)||H2(Ω))

(3.14)

(||u(s)||H2(Ω)+||v(s)||H2(Ω))≤C(||u(s)||L∞(Ω)+||v(s)||L∞(Ω))2·

(||u(s)||H2(Ω)+||v(s)||H2(Ω))

(3.15)

Furthermore, Lemma 2.1, (3.12), (3.13), (3.14) and (3.15) lead to

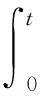
[1+log(1+||u(s)||H2(Ω)+||v(s)||H2(Ω))]ds

(3.16)

Let

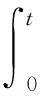
(3.17)

Then we have

J′(t)=C(||u(t)||H2(Ω)+||v(t)||H2(Ω))·[1+log(1+||u(t)||H2(Ω)+||v(t)||H2(Ω))]≤

CJ(t)[1+log(1+J(t))]≤C(1+J(t))[1+log(1+J(t))]

(3.18)

Hence (3.18) yields that

(3.19)

Hence Integrating (3.19), we obtain the estimate for ||u(t)||H2(Ω)+||v(t)||H2(Ω)of the form

||u(t)||H2(Ω)+||v(t)||H2(Ω)≤eαeβt

(3.20)

whereαandβare two constants indepent oft. Therefore, ||u(t)||H2(Ω)+||v(t)||H2(Ω)remains bounded on every finite time interval. Thus we must haveTmax=∞.

The proof of Theorem 1.1 is completed.