与行列式有关的一些比较

房喜明

（肇庆学院 数学与统计学院，广东 肇庆 526061）

0 前言

线性代数是高校理工专业本科学生的必修课程,比较思想在该学科中涉及的方面比较多.通过比较,有助于学生对线性代数有关理论和方法的掌握.行列式是线性代数的一个重要组成部分[1-5],也是整个线性代数理论的基础.熟练掌握行列式的有关理论和方法，对后续理论学习和学生逻辑思维能力的培养,以及其他学科学习均有益处.行列式的相关知识如下:数域、排列的定义,排列的逆序数,排列的一个对换,对换对排列逆序数的影响,n阶行列式的定义,特殊行列式的计算公式,行列式的性质,行列式中某个元素的余子式和代数余子式概念,行列式按某一行（或列）展开的定理,行列式的计算方法,求解线性方程组的克莱姆法则,用行列式的值判定系数矩阵为方阵的齐次线性方程组解的情况等.本文中,笔者探讨一些与行列式有关的比较思想.

1 一些与行列式有关的比较思想

1)关于行列式的定义,通常是在给出2阶和3阶行列式定义的基础上逐步定义n阶行列式[1,5].对于2阶和3阶行列式,为便于计算,给出了对角线法则的计算方法,但4阶以上的行列式没有对角线法则.针对随着阶数增加,计算行列式的对角线法则消失这种情况,可以用定义分别计算低阶和高阶行列式,并将之与对角线法则计算方法所得结果进行比较.

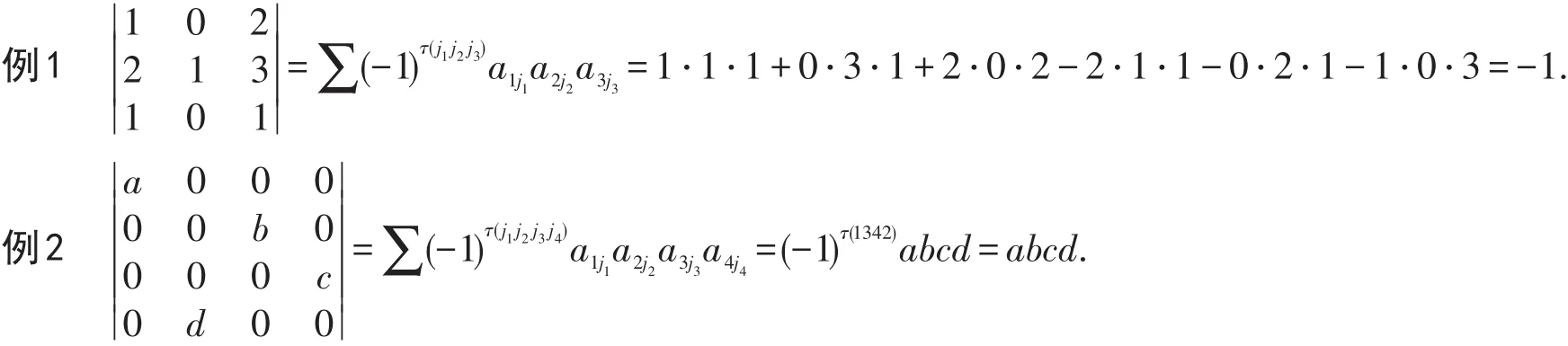
通过比较可以看出,前一个例子与用对角线法则计算结果一致,但第2个例子如果也采用类似3阶行列式的对角线法则计算,则是错误的.

2)在n阶行列式的定义中,有按行和按列取元素作乘积2种定义方法,这2种方法可以统一如下:每一项都是取自不同行、不同列的n个元素的连乘积,在其前面添加1个符号.这里存在比较思想,可以用实例显示出2种定义方法的一致性.如果用定义计算行列式,选取元素的方式会影响计算过程.

前一个例子分别按行和按列取元素作乘积计算同一行列式,显示2种定义方法一致.后一个例子采用按行选取元素的定义计算比较简便.

3)在行列式中确定某一项前面的符号存在比较思想.行列式中取自不同行、不同列的n个元素的连乘积要想成为行列式中的1项,其前面需添加1个符号,该符号的确定方法有3种.现给出实例将3种确定符号的方法进行比较,以体现三者的一致性.

例4确定5阶行列式中a21a34a15a42a53的符号.

4)在行列式计算方面存在比较思想.化为上(或下)三角形行列式和降阶法是计算行列式的2种常用方法,这2种方法也可以综合使用.下面以实例对这2种方法的特点与结果的一致性进行比较,以便更好地掌握这2种方法.

5)在行列式中某个元素aij的余子式和代数余子式相关问题存在比较思想.行列式中某个元素的余子式和代数余子式只与该元素的位置有关,而与该元素本身的值无关,也与该元素所在行和列的其他元素的值无关.为掌握和理解这一知识点,给出2个实例进行比较.

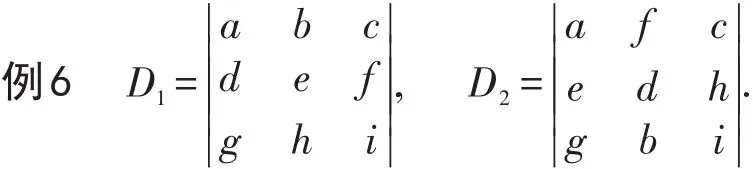
2个行列式中的(2,2)位置元素虽然不同,但这个位置元素的余子式和代数余子式都分别相同.

6)在行列式的计算与矩阵的初等变化方面存在比较思想.用行列式的性质计算行列式的值与用矩阵的初等行变换化矩阵为阶梯形或行最简形矩阵时,虽然是对2种不同对象的操作,一个用等号连接,另一个用箭头连接,但由于有些操作相同,故容易混淆.引入1个例子进行比较,可以区分两者的异同.

例8求行列式的值,并将矩阵化为阶梯形矩阵.

7)用行列式的值判断线性方程组解的情况存在比较思想.用行列式的值只能判断系数矩阵为方阵的齐次和非齐次线性方程组解的情况.其中对于非齐次线性方程组,用行列式只能判断有唯一解的情况,其他情况不能判断.这种方法与用矩阵的秩判断线性方程组解的情况相比,具有局限性.为区别这2种方法,现将其使用情况分别列表进行比较,详见表1.

表1 用矩阵的行列式的值或秩判断线性方程组解的情况对比表

2 小结

本文介绍了线性代数理论中一些与行列式有关的比较知识和实例,线性代数中其他涉及比较思想的知识还有:克莱姆法则与初等行变换法解线性方程组的比较;使用配方法和矩阵初等行列变换法求二次型的标准型的比较;有限维线性空间的线性变换在不同基下的矩阵的比较;实有限维线性空间上内积的不同定义方式(进而构成不同的欧氏空间)的比较等.通过比较,可以加深学生对线性代数理论和方法的掌握,为进一步学习打下良好基础.