观点传播的双世界网络模型

臧泽林，王万良

(浙江工业大学 计算机科学与技术学院， 杭州 310023)

(浙江省可视媒体智能处理重点实验室， 杭州 310023)

1 引 言

研究观点传播的客观规律有助于信息传播者更有效、更经济地使社会成员接受对自己有利的宣传信息，从而达到信息的社会推广的目的[1].因此，社会观点传播的研究在商业经营，政治竞争，观念引导中有着重要的作用.

谣言传播[2, 3]问题、热点话题传播问题[4, 5]、博客演化问题[4,6]都属于观点传播问题.这类问题有两个主要的难点需要解决:其一是如何确定观点传播所依赖的社会关系网络，其二是如何描述观点在社会关系网络的传播方式.

在社会关系网络方面，有一部分学者使用小世界网络模型来描述观点传播所依赖的关系网络[7].小世界网络模型是Watts等[8]提出的一种短路径、高聚度的复杂网络模型.具体地，小世界网络是规则网络和随机网络的中间产物，通过不确定的随机互联将集合内的节点进行链接[9].小世界网络常被广泛的应用于疾病传播[10]，电子邮件信息发送[11]，大脑结构分析[12]和人工智能[13]等领域.

小世界网络的应用十分广泛，但与此同时，普适的小世界网络而无法完全匹配特定问题[14].小世界网络虽然抽象了节点之间的一般联系，但是实验证明，在讨论特定问题(如观点传播问题)时会表现出对某些传播现象拟合误差较大的缺点.原因是小世界网络仅仅考虑了社会关系网络建立的随机性，并没有对社会关系网络建立所依赖的人文、地理等因素进行充分的考虑.因此在建立观点传播模型时有必要引入限制条件描述人文地理等因素对模型的影响：本文结合小世界网络模型，同时考虑关系世界与地理世界的相互影响提出了双世界网络模型.

双世界网络以地理位置为标准建立所有的传播节点，然后通过一定的信息传播规律，在传播节点上建立小世界性质的社会网络，从而建立一个更加灵活，更加直观的社会关系网络.

在描述观点在社会关系网络的传播方式方面.从单个节点对观点的接受情况的变化看来，一般存在泊松模型[15]和临界值模型[16, 17]两种模型，两者分别从连续和离散的角度，以从众心理的形式，对信息传播进行了微观描述.另外，为了方便计算机的仿真模拟，本文提出了置信法则来判别每一个节点的接受情况.精确的讲，本文使用正态随机的方式定义了节点的接受临界值，并使用元胞自动机的更新策略对节点进行同步更新，完成对整个社会传播模型的仿真.

为了合理地对评价双世界网络的通用性，本文使用5组数据集合[18]对双世界网络和小世界网络进行了对比仿真实验.首先，使用数据集合中的传播数据，通过最小二乘法确定两个模型的最优系数，而后对最优系数下的两个模型的仿真结果进行误差分析.分析结果显示，对于大部分数据，双世界网络模型可以更加精确的拟合真实数据点.这说明双世界网络模型相较小世界网络模型有更强的泛化能力.在最后本文对双世界网络模型的模型参数进行了敏感性分析.

基于上述要点，本文的主要贡献如下：

1)发展了小世界网络模型，利用地理因素对社会信息传播的影响，首次提出建立了更加直观，更加适用于信息传播模型的双世界网络模型，用以描绘信息传播机制.

2)依据从众心理，设计了置信法则.该法则可以有效的以微观的形式描述接受观点的动态过程.

3)通过计算机仿真详细的对社会信息传播进行了模拟，使用最小二乘法确定参数后对比了两种模型的优劣，并且对相关模型参数的敏感性做出了有效的分析.

2 双世界网络模型的建立

2.1 小世界网络模型

小世界网络模型[19]是一种复杂网络模型[20, 21]，其特性介于规则网络与复杂网络之间.WS小世界网络是Watts和Strogatz提出的建立方法建立的小世界网络.

可以按照如图1方法建立WS小世界网络：

1)首先将含有N个节点的最近邻耦合网络围城一个环，每个节点都有与其左右k/2个节点具有相邻的性质，式中k为节点的度，是偶数.

2)进行随机化的重连，以概率p随机的重连网络的每个边，保持一个端点不变，另一个端点取为网络中随机选择的一个节点.并且规定任意两个不同节点间只能有一条边.

小世界网络生成如图1所示，系数p规定了网络的随机性:

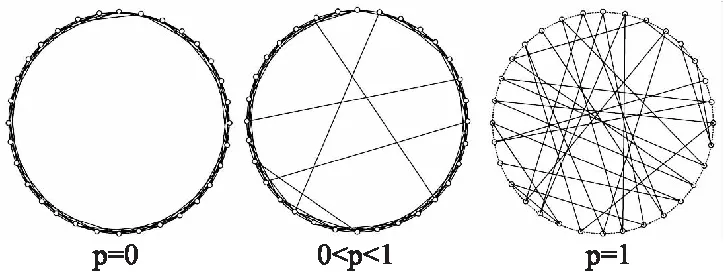
图1 小世界网络生成示意图Fig.1 Schematic diagram of small world network generation

在小世界网络中，p=0对应了完全规则的网络，p=1对应了完全随机的网络，通过调节p的值可以控制从规则网络到随机网络的变化，从而生成了生成小世界网络.

但是对于信息传播问题，小世界网络对人际关系的描述是模糊的.小世界网络默认网络中节点之间的联系是随机生成的，但是在现实中，即使是随机性最强的互联网用户之间关系也会受到地理等因素的制约.小世界网络并没有对节点的位置赋予明确的地理意义.由于在人际关系网络中，地理因素对社会社会关系的形成有着明确的限制作用，所以在模型中应该建立相应的机制.因此本文以小世界网络为核心并对其进行了发展，设计了双世界网络模型.

2.2 双世界网络模型的定义与数学描述

双世界网络模型是一种可以解决信息社会信息传播问题的复杂网络模型.模型通过建立一个物理关系与社会关系相互制约的信息传播网络，对社会信息的传播路径进行描述.

双世界网络模型可以表示为如下数学形式：

在无向有权连通图G(V,E)中，V代表联通图的范围，E代表联通图的链路，接受状态矩阵NETt满足方程(1).

NETt=NETt-1∪Bt

(1)

其中NETt代表t时刻网络对某信息的接受状态，图D(x,y)节点接受该信息时NETt(x,y)=1，此时该节点称为接受节点，不接受时NETt(x,y)=0，此时该节点称为不接受节点，公式(1)中Bt满足公式如(2)(3)(4)：

(2)

(3)

(4)

双世界网络模型的示意图如图2所示.

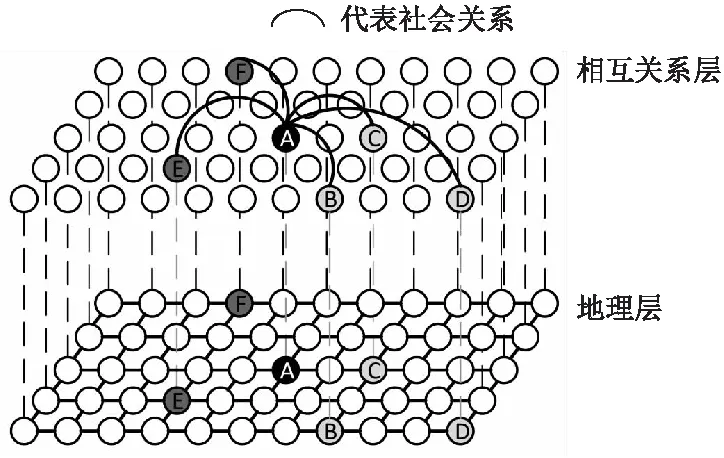
图2 双世界网络示意图Fig.2 Dual-world network diagram

对于任意节点，节点同时存在于两个世界.一个是地理世界，一个是相互关系世界.在地理世界中节点在地理上紧密的排列，这种排列的结构描述了节点之间的位置关系.另一个是相互关系世界，相互关系世界描述节点之间的相互的信息传递关系，比如图中节点A，在信息传递世界中与五个其他的节点存在信息交换的关系.但是这些与其有关系的节点不一定是其周围的节点.

2.3 置信法则

从众心里在信息接受与信息传播中的影响巨大.本文根据从众心里(从众心理是从众心理即指个人受到外界人群行为的影响，而在自己的知觉、判断、认识上表现出符合于公众舆论或多数人的行为方式)设计了置信法则.

置信法则是微观的衡量每个节点对信息接受态度的判别准则.为了模拟信息在社会中的传播情况，在通过双世界网络模拟社会中人际关系的同时，有必要设计置信法则对信息在人机关系网络中的传播情况做出分析.

置信法则描述如公式(5)所示.

(5)

其中，P(i,j)表示索引为(i,j)的节点对信息的相信情况，规定1为接受该信息.Nb表示其朋友圈中相信该信息的人数，Na表示朋友圈的总人数.αi,j为置信系数，在模型中所有节点的置信系数服从正态分布α～N(Jq,Jf).T(i,j)为置信转移矩阵，用来描述本次传播使不相信消息的人接受消息的情况.在所有节点的置信转移矩阵更新完毕后通过或运算对矩阵P进行更新.

2.4 双世界网络模型的参数设计

不同的信息传播在不同的社会结构上会产生不同的结果.其中的差异在双世界网络模型中表现在不同的模型参数上.本文定义模型的参数如表1所示.

表1 变量名、含义对照表Table 1 Comparative table of variable names and meanings

表中定义了朋友关系数量Nf、交友距离Lf、仿真区域[Wc,Wk]、节点易信度均值Jq、节点易信度方差Jf与媒体宣传力度Mp六个重要的参数.其中朋友关系数量Nf、交友距离Lf、仿真区域[Wc,Wk]为双世界网络模型参数，是用来描述社会关系网络的参数；节点易信度均值Jq、节点易信度方差Jf与媒体宣传力度Mp是置信法则传播参数，用来描述信息传播过程的参数.

具体地，Nf用来描述在双世界网络中，每个节点与外界节点建立联系的数量.该联系是单向的，也就是说节点A与节点B有连接关系并不代表节点B与节点A有着相同的连接关系.这也反映了社会网络中存在的不对等的信任现象.

Lf描述建立上述信任关系的最长距离，在现实的社会网络中，代价过大(表现在地理世界)的信任关系是无法维系的，即使在网络发达的当代，大多数人的信任的人都存在于一定范围内.另外，对于不同的信息，人们信任的圈子也会不同.比如，比较私密的问题信任的范围比较小，人们求证的渠道也比较小；而比较公开的问题，人们的信任的范围会比较大，也可以进行比较全面的求证.

为了方便计算机模拟，设定仿真区域为正方形，区域的大小为[Wc,Wk]，Wc与Wk分别代表仿真范围的行数与列数.

Jq、Jf描述每个节点在置信法则下进行更新的置信度的αi,j的平均值与方差，当αi,j较大时，节点更容易接受某一观点.Mp为模型迭代时的媒体推动，在传播的开始，模型模拟会先将易信的一些节点设置为相信节点作为整个模型的初始推动力，这样的过程被视为社会媒体对传播的推动作用.

3 双世界网络的计算机实现

双世界网络的实现分为双世界网络的生成算法和双世界网络的迭代两部分.

3.1 双世界网络模型的生成

模型通过MATLAB 2015软件进行实现，流程图见图3.

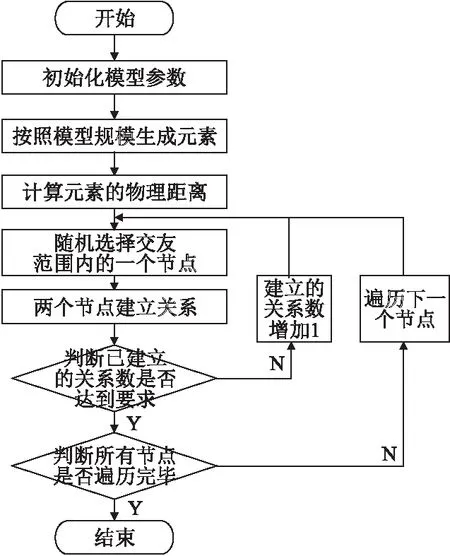
图3 双世界网络流程图实现Fig.3 Implementation of dual-world network flow chart

生成算法主要包括参数初始化、节点生成和关系生成三个部分：

参数初始化部分在程序开始前将上文中定义的参数进行初始化，并保存在计算机的内存中.

在节点生成部分，程序会生成一个大小为[Wc,Wk]的矩形排列的节点.并且根据此节点一一对应的生成一个朋友节点列表和易信程度列表.朋友节点列表根据参数Nf和Lf随机确定每个节点的朋友节点.易信程度列表根据参Jf和Jq确定每个节点的易信度.

生成朋友节点的过程中，使用欧式距离，公式如下：

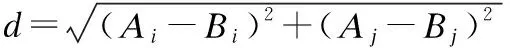
(6)

式中d为生成的距离，Ai，Aj，Bi，Bj代表A，B两点的横纵坐标.

在建立网络时，根据随机算法在交友范围内确定朋友节点，直到所有的节点都被确定了朋友节点.

3.2 双世界网络模型的迭代

双世界网络的迭代算法流程图如图4所示.

每次遍历按顺序逐个访问对某一观点持不接受意见的节点，判断其朋友节点中的相信百分比是否满足置信法则.如果满足置信法则(Nb/Na>αi,j)将该节点更新为接受节点.节点的更新形式设定为异步更新，即在完成每次遍历后统一更新节点的相信情况.

当模型中再没有可供更新的节点时，仿真完成.

4 模型的仿真结果

本节首先阐述小世界网络模型与双世界网络模型在拓扑特性上的联系与差别，然后对双世界网络模型描述的传播过程进行图形仿真和数值论证，最后对模型进行了敏感性分析.

图4 双世界网络遍历流程Fig.4 Dual-world network traversal process

4.1 双世界网络模型的拓扑特性探讨

双世界网络可以看成是小世界网络的一种拓展，下面通过仿真实验来分析双世界网络模型与小世界网络模型的拓扑特性的关系.

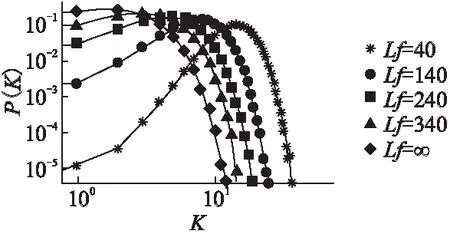
图5 双世界与小世界网络度的分布随模型参数交友范围的变化图Fig.5 Mapping of the distribution of dual-world and small world networks with model parameters

度[14]是单独节点的概念，节点的度是指与该节点相关的边的条数，也就是与该节点连接的其他的节点的数目.度分布是指网络中的节点具有的度，一般记作P(k).双世界网络与双世界网络的度分布图如图 5所示.

图5中描绘了不同模型交友范围Lf下的度的分布函数，当Lf较小时，度的分布接近一个正太的分布，朋友节点数过多或者过少的节点的个数都比较少.随着Lf的增加，双世界的度分布越来越接近于小世界网络的度分布，即表现为度较小的节点较多，度较大的节点较少.当Lf趋向于正无穷时，在度分布的表现上，双世界网络与小世界网络相同.

聚类系数[14]表征的是网络的聚类特性，也就是群落特性，一般假设网络中的节点i与ki条边关联，i节点中最多可能有ki(ki-1)/2条边，而i节点实际存在的边数是与总的边数Ei的比定义为节点的聚类系数Ci的公式为：

(7)

式中ki表示i节点的边数.

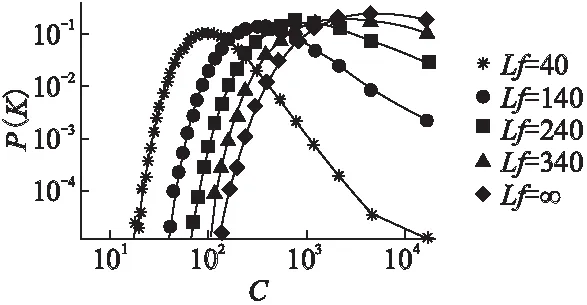
图6 双世界与小世界网络度的聚类系数随模型参数交友范围的变化图Fig.6 Clustering coefficient of dual-world and small world network with the range of model parameters

图6中描绘了不同模型参数交友范围Lf下的聚类系数的分布函数，当Lf较小时，聚类系数集中在100左右，过大或者过小的频数都不高.随着Lf的增加，双世界的度分布越来越接近于小世界网络的单调递增的分布函数分布，即表现为度较小的节点较多，度较大的节点较少.当Lf趋向于正无穷时，双世界网络与小世界网络的度的分布相同.

实际的网络虽然具备小世界性，但是并不是完全随机的小世界特性，而是会受到地理因素的限制.由于受到地理因素的限制，每个人无法随机的选择自己的信任节点，导致信任节点较小的节点的数量减少，从而产生与小世界网络的差异.双世界网络模型能够有效的描绘这一现象，在地理限制和小世界性中做出优秀的权衡.

4.2 观点传播的图像仿真

双世界网络模型与小世界网络模型相比具有更加优秀的可视性.由于其模型的建立遵循地理限制，所以可以通过二维图像容易的对模型的传播情况进行视觉上的展示.图 7所示的是观点某一在方形区域中传播情况.

图7 信息传播情况仿真图Fig.7 Simulation diagram of information dissemination

图7中4幅图片分别展示了时间单位为1、5、7、17时的对某一观点(下称观点A)的群众接受情况，其中白色节点代表并未接受观点A的节点，黑色代表接受观点A的节点.可以看到在传播的开始阶段(T=1)，经过媒体的宣传，已经有少数的人先接受了观点A.在媒体宣传过后，消息进入社会传播阶段，观点A随着时间的推移，开始被社会广泛接受.在T=20时，大多数的节点都接受了观点A，观点A的传播结束.

4.3 观点传播的数值仿真使用的数据集合介绍

在互联网时代，使用易于采集的大型社交媒体的转发数据代替无法精确采集的社会传播数据可以有效的降低数据采集的难度，与此同时互联网中所采集的社会传播数据也能够很大程度上反应出社会观点传播的趋势和动态.

因此，本文数值仿真所使用的数据集合是由唐朝生[18]在博士论文中使用北京大学可视化与可视分析研究组开发的 PKUVIS 微博可视分析工具(Weibo Events)，抓取微博中的热点事件的传播事件的五组传播数据集合.

其中数据集合1中的数据为"昆明火车站暴力袭击事件" 中VIP 用户对谴责"昆明火车站暴力袭击事件微博消息"的转发情况数据.数据集合2中的数据为全体网民对谴责"昆明火车站暴力袭击事件微博消息"的转发情况数据.数据集合3是2014年3月8号发生的马来西亚航空370号班机空难事件消息转发情况数据.数据集合4是在2013年发生的"美国同性恋立法事件"中微博VIP 用户的转发情况数据.数据集合5是在2013年发生的"北海宰客事件"中所有用户对谴责"昆明火车站暴力袭击事件微博消息"的转发情况数据.

仿真使用的数据集合的统计表如表2所示.

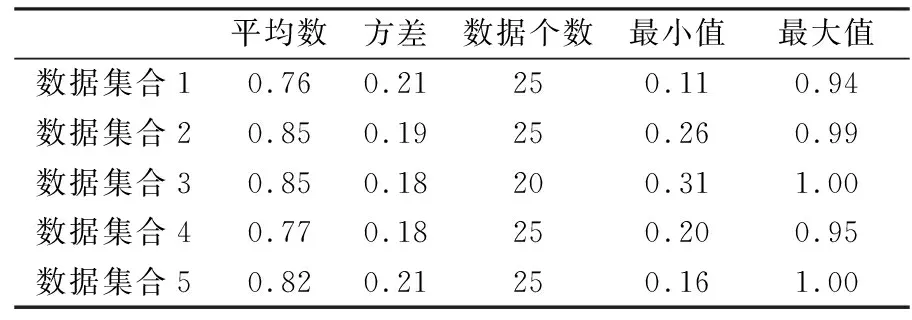
表2 仿真使用的数据集合的统计表Table 2 Statistical table of data sets used for simulation

表中列出了5个数据集合中相信人数百分比的平均数、方差、数据个数、最小值、最大值等5个统计变量.由于数据集合中数据的数量级差异悬殊，为了对5组数据集合进行有效的横向对比，将数据通过公式(8)映射到0-1区间.

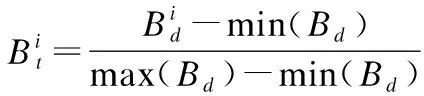
(8)

为了解决每个数据集合的数据个数不统一的问题，本文使用插值算法对数据个数较少的数据集合进行插值扩充，使各个数据集合的数据个数相同，方便运算与比较.

4.4 观点传播的数值仿真与对比

数据在上述数据集合的基础上，本文通过最小二乘法分别对双世界网络与小世界网络的参数进行拟合.使用最小二乘法分别调整模型参数后得到的仿真图像(只画出数据集合一的图像)如图 8所示.

图8 小世界网络与双世界网络拟合效果对比图Fig.8 Comparison of small world network and dual-world network fitting effect

图8中横坐标代表时间轴，纵坐标代表相信人数占总人数的百分比.虽然社会的传播情况受到信息的特点、当地传统文化、时间与地点等因素的影响，有限数量的仿真结果并不能完全的反应传播模型的优劣，但是该结果同样可以反映出模型对不同的传播数据的适应能力.

具体地，图中黑色圆点代表数据集合中的数据，图中实线代表了双世界网络经过参数最优化的传播数据，虚线代表了小世界网络经过参数优化的传播数据.在不增加附加约束的情况下，可以看到小世界网络无法像双世界网路一样逼近给定目标数据集合，这种现象在本文给出的所有仿真结果中拥有共性.

表3 使用最小二乘法对双世界网络与小世界网络进行调参后的最优参数与误差统计表Table 3 Optimal parameters and error statistics for dual-world networks and small world networks using least squares method

使用最小二乘法对所有的5个数据集合进行参数调整，并且使用调整后的参数进行计算机模拟仿真，仿真的结果和经过调整的参数统计如表3所示.

表3中分别列出了双世界网络模型和小世界网络模型的仿真结果，结果显示双世界网络模型的仿真结果平均误差、标准差与最大误差分别在2.3%，2.5%与6%左右，明显小于小世界网络的平均误差、标准差与最大误差.不同的数据集合对应着不同的消息在不同的社会网络与地理限制下进行传播，因此数据集合确立的模型参数也并不相同.比如有些消息只能在较为亲密的人群间进行传播，而有些消息可以传播给更多的节点.在本文的数据集合中，数据集合四由于传播节点的平均数Nf较低，相互之间给予了更大的信任(Jf更大)，更加倾向于私密信息的传播情况.

4.5 模型的敏感性分析

在固定某一观点(下称观点A)传播的其他参数的基础上，本文改变Nf，与Lf为进行敏感性的分析.分析见图9图10.

图9中每一张图片都描述了在Lf的值为特定值的情况下，接受观点A的百分比的变化情况.可以看到，当Lf过小时，会使得社会团体的分散程度过低，造成信息过渡集中，与信息流通不畅.这也解释了为何当信息媒介不发达时并不会产生世界性的大新闻的现象.随着人们的交友范围的提升，信息拥有了更大的传播空间.随着人们交友范围的增加，信息的传播速度会出现飞跃式的提升.但是随着交友范围的进一步提升，信息传播的效率又会出现非线性的下降.原因是，当交友范围大过某一阈值后，小世界现象消失，社交网络趋向于随机网络.在随机网络型社会关系的链接下观点要么在极短的时间内被社会接受，要么在极短的时间内被世界拒绝，不存在本文研究的传播过程.

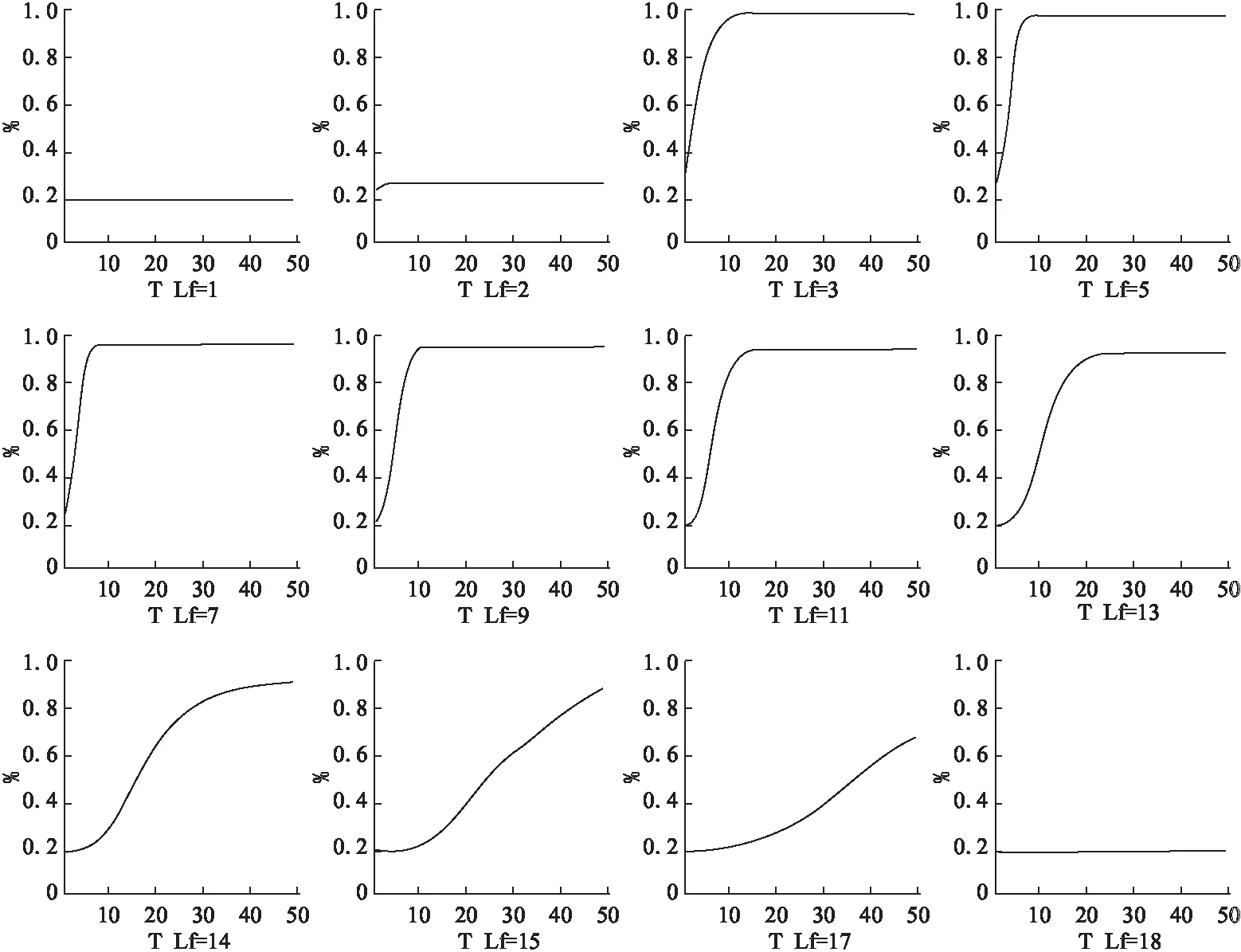
图9 交友范围Lf敏感分析图Fig.9 Lfsensitive analysis chart of dating range

图10 朋友个数Nf敏感分析

如图10所示为节点朋友数量对传播模拟的影响.结果显示，在其他条件不改变的情况下，节点的朋友数越多，就会使得社会关系越紧密，从而会带来传播速度的相应提高.但是在仿真的结果中可以看到朋友数的参数会产生屋顶效应，也就是说当朋友数到达一定的较大值后，传播的结果对朋友数的敏感性不高.

5 结 论

本文发展了小世界网络模型，充分考虑了地理因素对社会信息传播的影响，提出了双世界网络模型.并且依据从众心理和等信息传播特点，设计了置信法则.该法则可以有效的以微观的形式描述接受观点的动态过程.

为了衡量置信法则和双世界模型优势，本文通过计算机仿真对社会信息传播进行了模拟.带入实际的信息传播数据，使用最小二乘法确定两种模型各自的最优参数.并对比了两种模型的仿真误差.结果显示双世界网络模型仿真结果产生的误差的均值与方差均优于小世界网络模型.说明双世界网络模型对于不同的信息传播数据集合有着更好的拟合性.