基于FLAC3D方法对某边坡的稳定性分析
2018-10-16李勇辉朱伯文唐江涛
李勇辉,孙 勇,朱伯文,唐江涛
(1.贵州大学 国土资源部喀斯特环境与地质灾害重点实验室,贵阳 5500033; 2.成都理工大学 地质灾害与防治与地质环境保护国家重点实验室,成都 610059)
西南地区主要是山区,在修建公路铁路的过程中会遭遇大量的边坡。而边坡的稳定性分析是重中之重,首先要分析该边坡的稳定与否,如若需要进行开挖,则需要对该开挖方案进行稳定性分析,从而判断该方案的可靠度与可行性。近年来,数值模拟在边坡稳定性分析中得到大量的运用,其中FLAC3D软件因其模拟结果与实际情况更加相符,从而得到更广泛的应用。
1 FLAC3D原理
FLAC3D是由美国itasca公司开发的一种模拟仿真计算软件,是对二维有限差分程序FLAC2D的扩展,能够对土体、岩石和其它材料进行三维结构的受力特性模拟和塑性流动分析。通过对三维网格中的多面体单元进行不断调整来拟合实际的结构单元。单元材料主要有线性和非线性两种本构模型,在外力作用下,当材料达到屈服流动后,网格可以产生相应的变形和移动(大变形模式)。FLAC3D主要采用显式拉格朗日算法和混合-离散分区技术,能够十分准确模拟材料的塑性流动和破坏。因为不用形成刚度矩阵,所以该软件用较小的内存空间就可以求解相当大范围的三维问题。FLAC3D主要有三大类模型:开挖模型、弹性模型和塑性模型。FLAC3D网格中的每个区域都可以赋予不同的材料模型,并且可以指定材料参数的统计分布以及变化梯度。而且模型中还包含有节理单元,也称之为界面单元,可以模拟两种以及多种材料界面,不同材料性质的间断特性。节理允许发生滑动或者分离,因此能够用于模拟岩体中的断层、节理和摩擦边界。FLAC3D中的网格生成器gen,可以通过匹配、连接在网格生成器中生成局部网格,从而方便地生成模拟所需要的三维结构网格。还可以自动产生交叉结构网格(比如说相交的巷道),三维网格由整体坐标系X、Y、Z系统所确定,不同于FLAC程序是由行列方式确定。这就提供了比较灵活的产生和定义三维空间参数。FLAC3D计算步骤为建立网格,划分网格,选择本构模型,赋参数,选择初始边界条件达到原始平衡,模拟开挖监测坡内响应[1-2]。
2 研究区三维模型建立
2.1 模型的建立
正确的地质模型是计算的基础,在计算中不可能也无必要将所有细节考虑进去,因此对工程地质条件的深入认识与抽象是建立合理地质概化模型的前提和关键。研究区边坡顺拟建公路走向约121 m,垂直公路走向约151 m,最大垂直开挖深度约28 m。边坡上堆积的残坡积物较薄,基本为一岩质边坡,岩性主要为白云岩、泥质白云岩、泥岩等三大类,根据现场调查,研究区边坡并无大型断层,结构面面等,因此不考虑断层及结构面等的影响,为模型长度取121 m,宽度取151 m,底部高程为800 m,参照坝址区工程地质平面图、剖面图以及边坡岩级分带图等,建立研究区数值模型。FLAC3D数值模型建立方法大体上有两种,一种是通过前处理较为方便的其他软件建立数值模型并划分网格,将网格节点和单元信息导出,经处理后再导入FLAC3D中[3];另一种是直接在FLAC3D程序中采用堆砌法生成模型,本文采用第一种方法,利用cad-surfer-ansys-flac联合建模方法,建立其数值模型。见图1。

图1 研究区三维模型Fig.1 Three dimensional model of research area
2.2 模型本构关系的选取
数值计算中,将岩土体看作理想弹塑性材料,屈服准则采用内置的Mohr-Coulomb准则,即:
(1)
式中:NΦ=(1+sinφ)(1-sinφ);σ1为最大主应力;σ3为最小主应力;φ为内摩擦角;C为内聚力。
若fs<0,表示岩体发生剪性屈服;fs≥0,表示岩体未发生剪性屈服。
当法向应力为张应力时,则超出了莫尔-库仑准则的力学有效性范围,此时要求最小主应力不得超过岩体的抗拉强度,否则岩体将出现张性屈服,其判别公式为[4]:
ft=σ3-σt
(2)
若ft≥0,表示岩体张性屈服;若ft<0,表示岩体未发生张性屈服。
对于FLAC-3D数值计算所要求的参数体积模量(K)和剪切模量(G)可以通过下式进行换算[5]:
(3)
(4)
式中:E为弹性模量;γ为泊松比。
实际上,在FLAC3D中使用M-C本构模型时也可直接输入弹模和泊松比,程序可实现自动换算。
2.3 模型边界的选取
FLAC3D提供两种应力边界条件,一种是位移(速度)边界条件,一种是应力边界条件。应力边界一般用于需考虑原岩应力的情况下。对模型底部采用完全约束,约束其3个方向的自由度;而对模型的前后左右均只作单向约束,即仅约束水平方向速度而不约束其竖向速度。除此之外,由于上部房屋的影响,因此需要考虑施加均布载荷,就需要使用应力边界荷载条件。这样,岩土体在生成自重应力阶段可发生自由沉降,符合实际情况。
3 边坡稳定性分析
3.1 自然斜坡稳定性分析
为了解自然斜坡在天然条件下的稳定性情况,考虑上部房屋荷载情况下斜坡在自身重力作用下的稳定性,分别进行斜坡应力分析、斜坡变形分析以及斜坡稳定性分析
3.1.1 斜坡应力分析
斜坡应力分析主要从斜坡的重力场以及最大最小主应力场3个方面进行,斜坡重力场模拟图见图2-图7。
由图2-图3可知,坡体应力量值范围在-2.04~0.13 MPa,坡体应力分布均匀,自上而下逐步增加,应力最大值分布在斜坡地面,坡面由于施加有房屋荷载,所以在一定范围内,坡表的应力值较大,极少数地方出现拉应力。
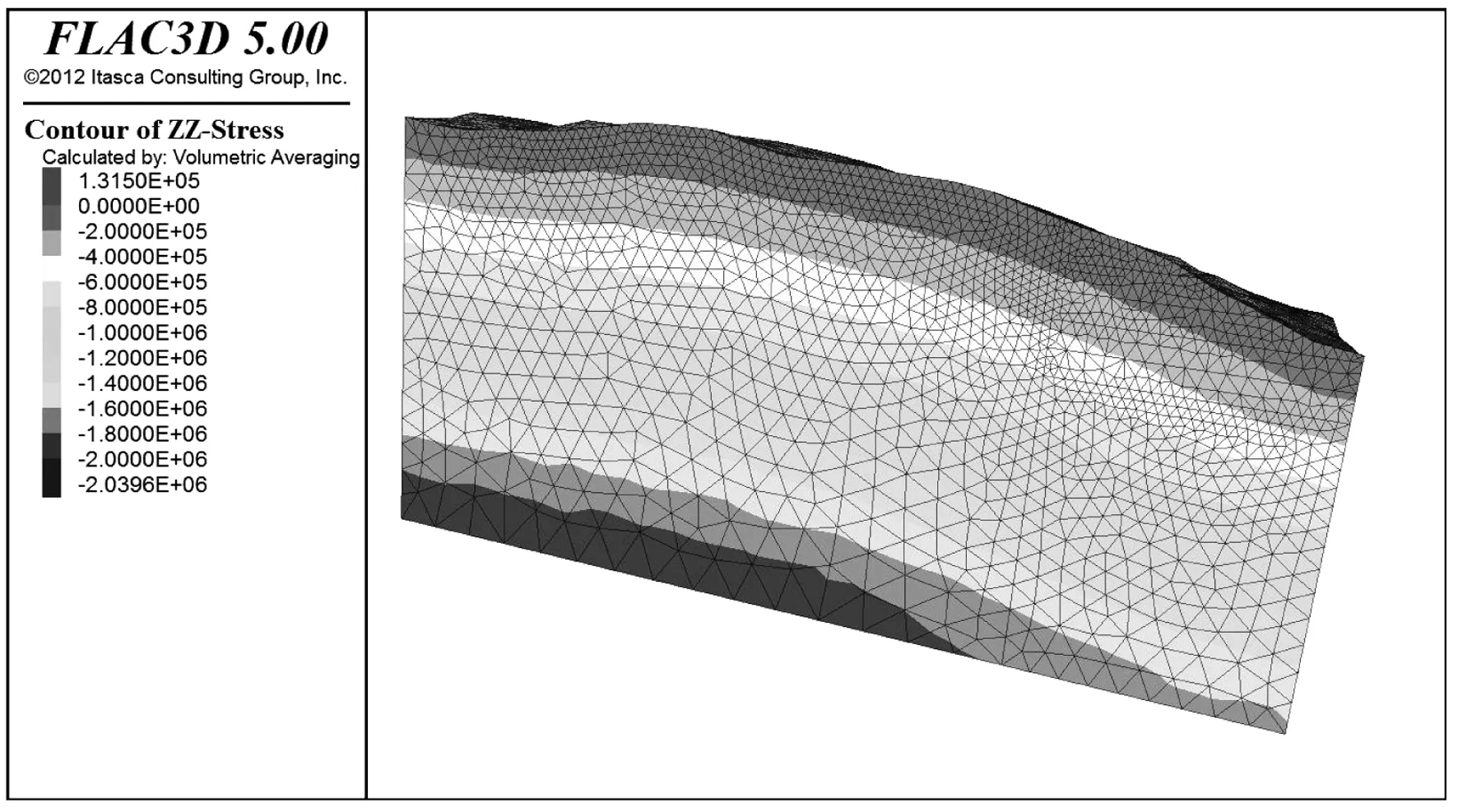
图2 坡体自重应力云图Fig.2 The slope self-weight stress nephogram

图3 坡表自重应力云图Fig.3 The slope surface self-weight stress nephogram
由图4-图5可知,边坡最大主应力的量值范围为-0.85~0.58 MPa,坡体的最大主应力位于底面,与重力方向的应力相似,坡体中大主应力分布均匀,由上往下逐渐增大,坡体中无应力集中现象。在坡表最大位移云图中可以知道,位于右侧的局部地区出现了拉应力。主要是地形起伏大以及层面间的接触面处。

图4坡体最大主应力云图Fig.4 The slope max principal stress nephogram

图5 坡表最大主应力云图Fig.5 The slope surface max principal stress nephogram
由图6-图7可知,斜坡的最小主应力的量值范围为-2.04~0.09 MPa,坡体中最小主应力分布与重力分布类似,由上到下逐渐增大,均匀分布。坡表的最小主应力云图可知,只有作用均布荷载的地方应力出现一点异常,其他都正常。
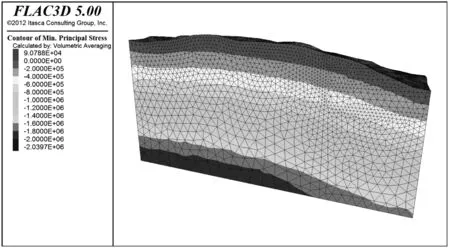
图6 坡体最小主应力云图Fig.6 The slope mini principal stress nephogram

图7 坡表最小主应力云图Fig.7 The slope surface mini principal stress nephogram
3.1.2 斜坡变形分析
坡体变形一定程度上可以反映边坡的稳定状态,斜坡的变形分析主要从X方向以及Y方向的位移入手,模拟结果图见图8-图9。
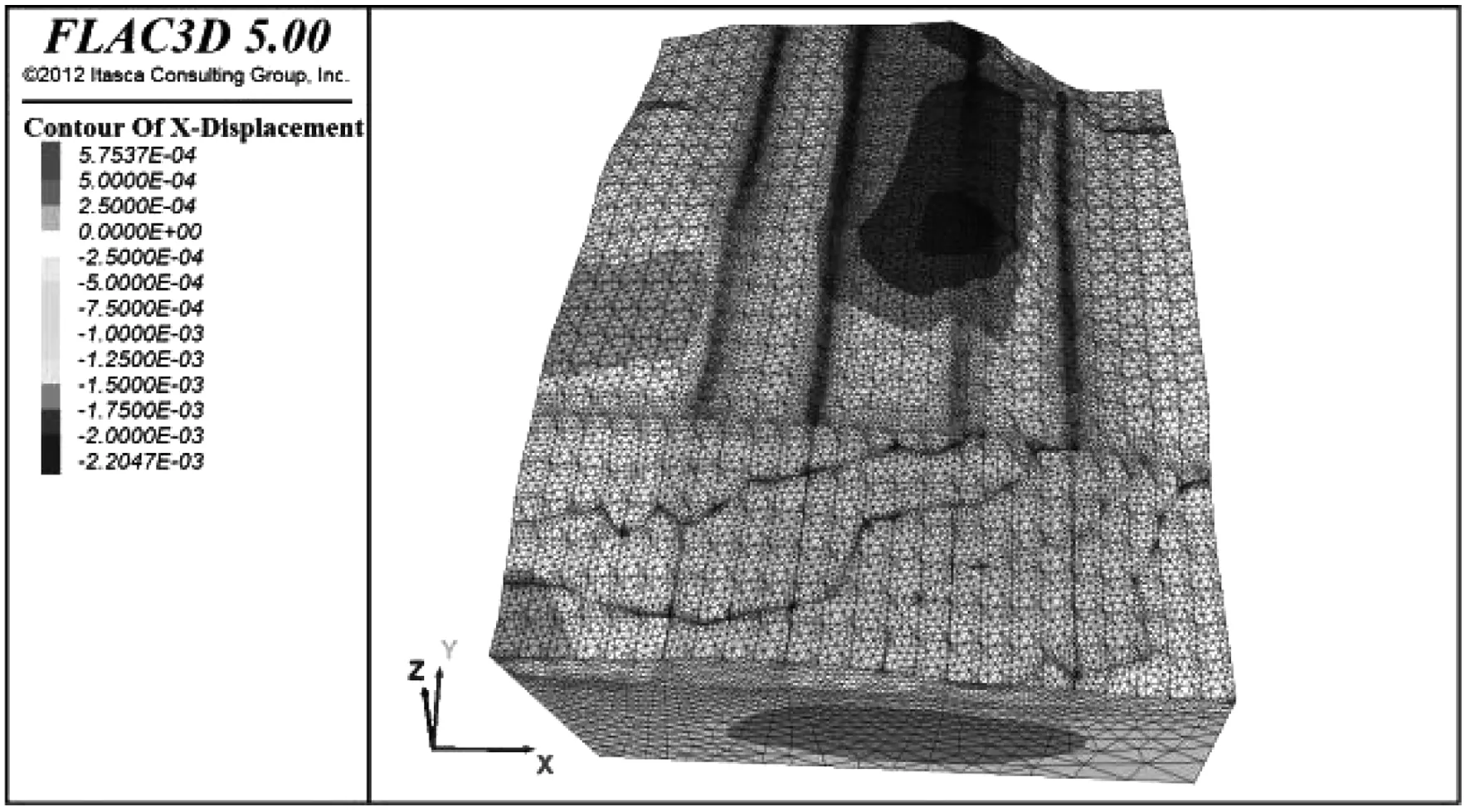
图8 斜坡X方向位移云图Fig.8 X direction displacement nephogram of slope
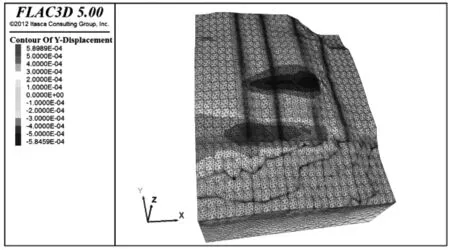
图9 斜坡Y方向位移云图Fig.9 Y direction displacement nephogram of slope
图8-图9为数值模拟结果图,从作图可以知道,坡表X方向的最大位移为2.2 mm,主要集中不同岩性相交位置处,坡表Y方向最大位移为0.6 mm,主要集中在施加均布荷载的前段。自然斜坡的变形量非常小
3.1.3 斜坡稳定性分析
塑性区以及剪应变的增量可以反映边坡的稳定状态,一般来说,边坡塑性区越大,深度越深,则对边坡的不离程度也相即增大,对模拟结果进行切片,分别沿斜坡横向以及纵向切片,得到横向以及纵向的最大剪应变速率。见图10、图11。
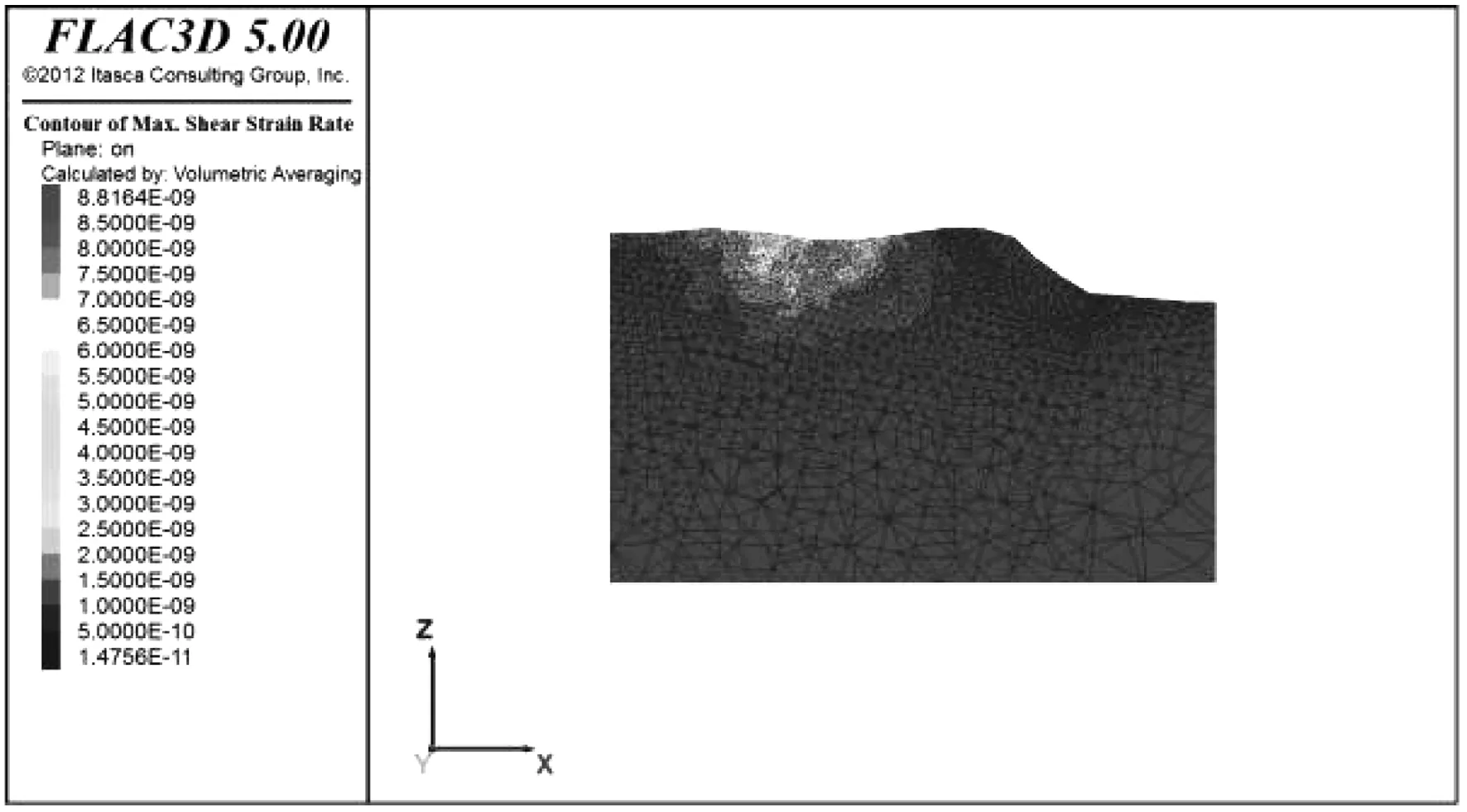
图10 斜坡横向剪应变速率云图Fig.10 Transversal shear strain rate nephogram of slope
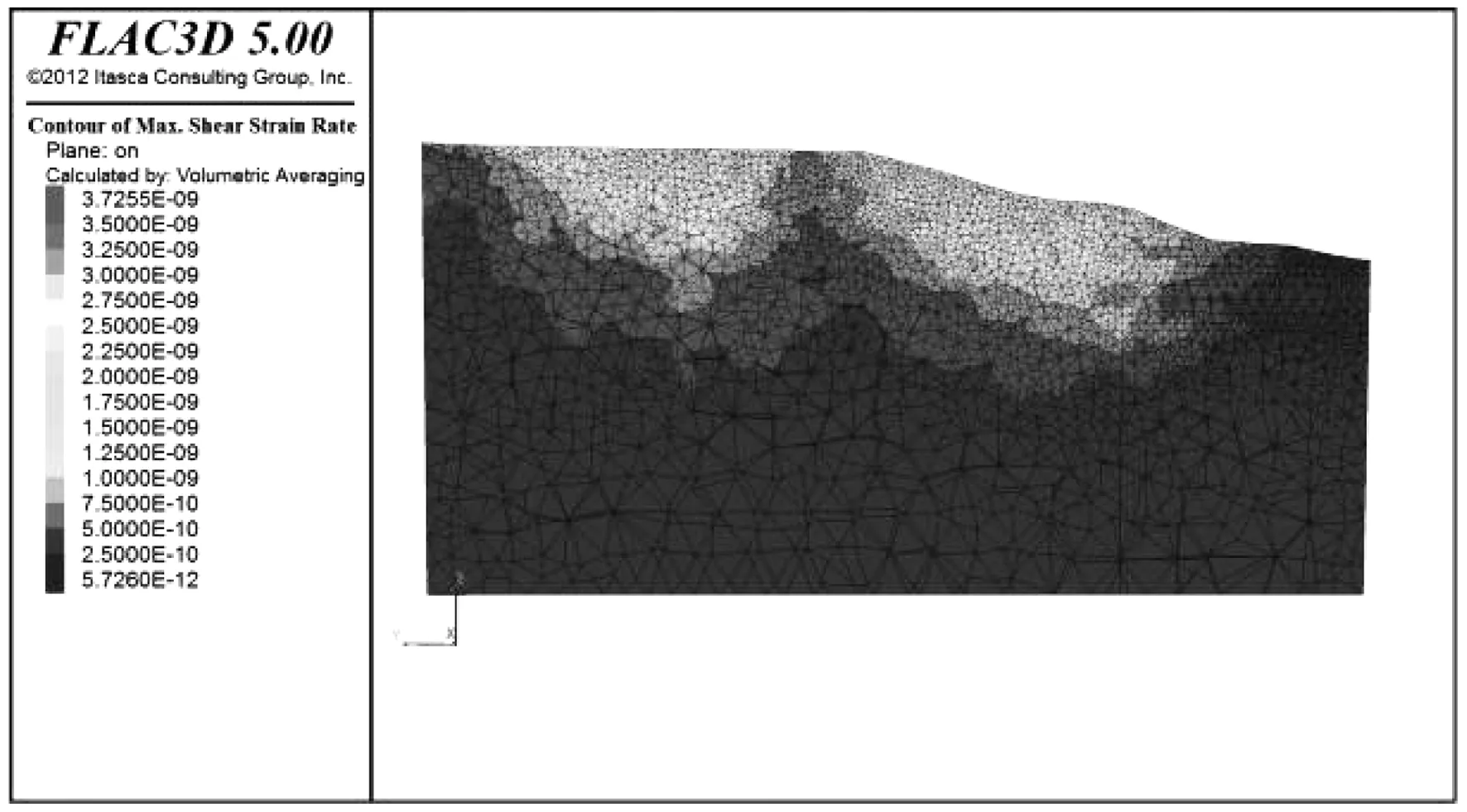
图11 斜坡竖向剪应变速率云图Fig.11 Longitudinal shear strain rate nephogram of slope
由图10、图11可知,横向以及竖向的剪应变速率都非常小,几乎可以忽略不计,说明斜坡处于一个稳定的状态。
3.2 开挖条件下边坡稳定性研究
开挖方案为沿着开挖线垂直开挖至指定高程843.0 m处,最大的开挖深度局部可以达到28.0 m,开挖将会形成陡立边坡,模拟开挖之后边坡的稳定性以及变形。
首先在自然斜坡达到上述自重平衡的条件下,对原本存在的位移进行清零处理,以便可以清楚掌握在开挖情况下边坡产生的位移情况。
3.2.1 边坡应力分析
开挖边坡主要从最大主应力、最小主应力进行初步分析,分析是否存在应力集中部位,模拟结果见图12-图16。
由图12-图13可以看出,开挖情况下,坡体的最大主应力总体分布较均匀,自上而下逐步增加,最大主应力的量值范围为0.055~-0.85 MPa,但在开挖的坡脚出现了应力集中的情况,应力的大小约为-0.2 MPa。此外,在坡表作用于均布荷载的地方,应力也出现“异常”,其他地方都应力分布形式都为正常情况。
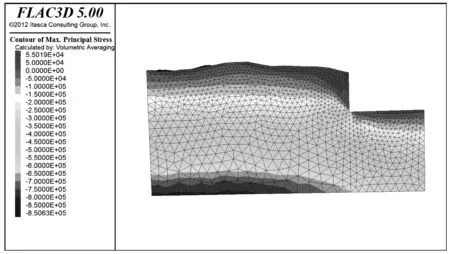
图12 坡体最大应力分布图Fig.12 Max stress distribution in slope
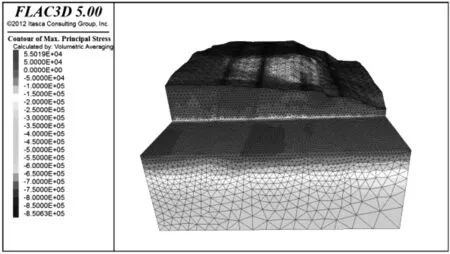
图13 坡表最大应力分布图Fig.13 Max stress distribution in slope surface

图14 坡体最小应力分布图Fig.14 Mini stress distribution in slope
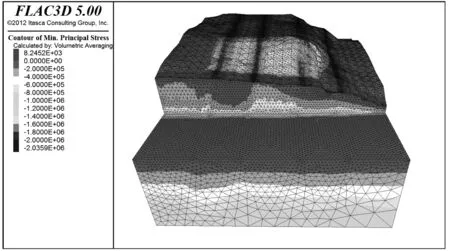
图15 坡表最小应力分布图Fig.15 Mini stress distribution in slope surface
坡体最小主应力图的分布形式与坡体最大主应力分布形式类似,应力分布总体均匀,自上而下应力逐渐增大,应力分布的量值为0.008~-2.054 MPa,最小主应力的最大值分布在坡地,最小值分布于坡表面,在开挖的坡脚段也出现了应力集中的现象,作用于均布载荷的上部应力“异常”,边坡其他部位都处于正常状况。
从图16可以看出,边坡的最大剪应力分布在开挖段坡脚部分,剪应力的量值范围为0.005~0.682 MPa,图16红色区域就是最大剪应力分布区域,值的大小约为0.67 MPa。综合以上分析可知,在开挖坡脚部分出现应力集中的情况,可能对边坡的稳定性造成不小的危害,需要进行进一步的分析论证。
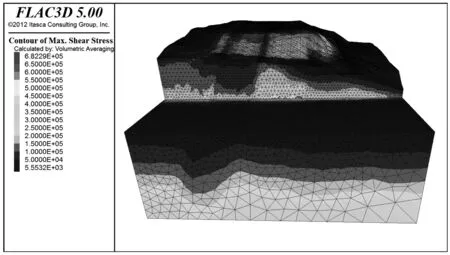
图16 边坡最大剪应力分布图Fig.16 Max shear stress distribution of slope
3.2.2 边坡变形分析
对边坡的变形分析主要从开挖之后坡体在X以及Y方向的位移及其位移值,布设的监测点进行分析。见图18-图19。
从边坡X方向的位移云图可知,X方向最大位移量值方位为-13.6~12.5 mm,最大位移主要是层面接触方向以及均布荷载作用的边缘,如图左上角红色区域为均布荷载作用边缘处。在Y方向的位移云图中可知,位移的量值范围为3.2~-93.2 mm,最大位移集在相对岩体力学性质软弱处,在边坡的右侧,由于其开挖量比较小,边坡Y方向的位移值比较小,呈现mm级别的,但是在边坡左侧由于上部房屋的作用以及开挖高度大的影响,边坡Y方向的位移呈cm级别,最大位移为9.3 cm,边坡处于不稳定状态。
3.2.3 边坡稳定性分析
塑性区以及剪应变的增量可以反映边坡的稳定状态,一般来说,边坡塑性区越大,深度越深,则对边坡的不离程度也相继增大,对模拟结果进行切片,分别沿斜坡横向以及纵向切片,得到横向以及纵向的最大剪应变速率。见图19-图22。

图17 边坡X方向位移云图Fig.17 X direction displacement nephogram of slope
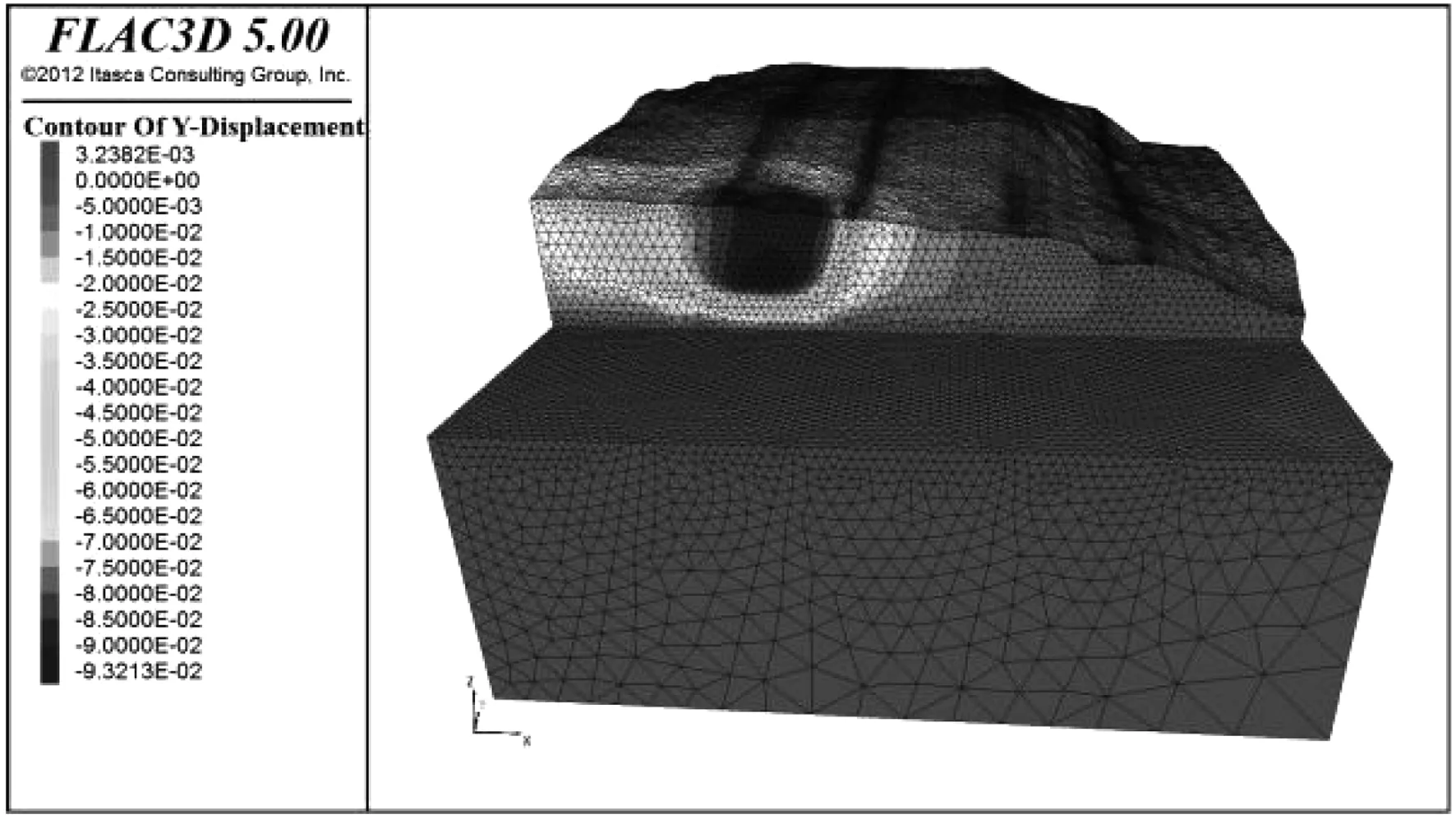
图18 边坡Y方向位移云图Fig.18 Y direction displacement nephogram of slope
由图19-图22可以看到,X方向的最大剪切应变处于开挖坡脚线附近,其量值范围为1.00×10-6~8.48×10-6,Y方向的最大剪切应变位于坡表,量值范围为1.00×10-7~9.50×10-7。从Y方向塑性区的分布云图可以知道,开挖线后约20 m范围内岩体处于受剪切的状态,受剪区与开挖线的夹角大约为45°。在X方向塑性区分布云图可知,在高程为850.0 m以上的岩体基本处于受剪切状态,表面岩体受拉张作用。

图19 X方向最大剪应变云图Fig.19 X direction max shear strain nephogram
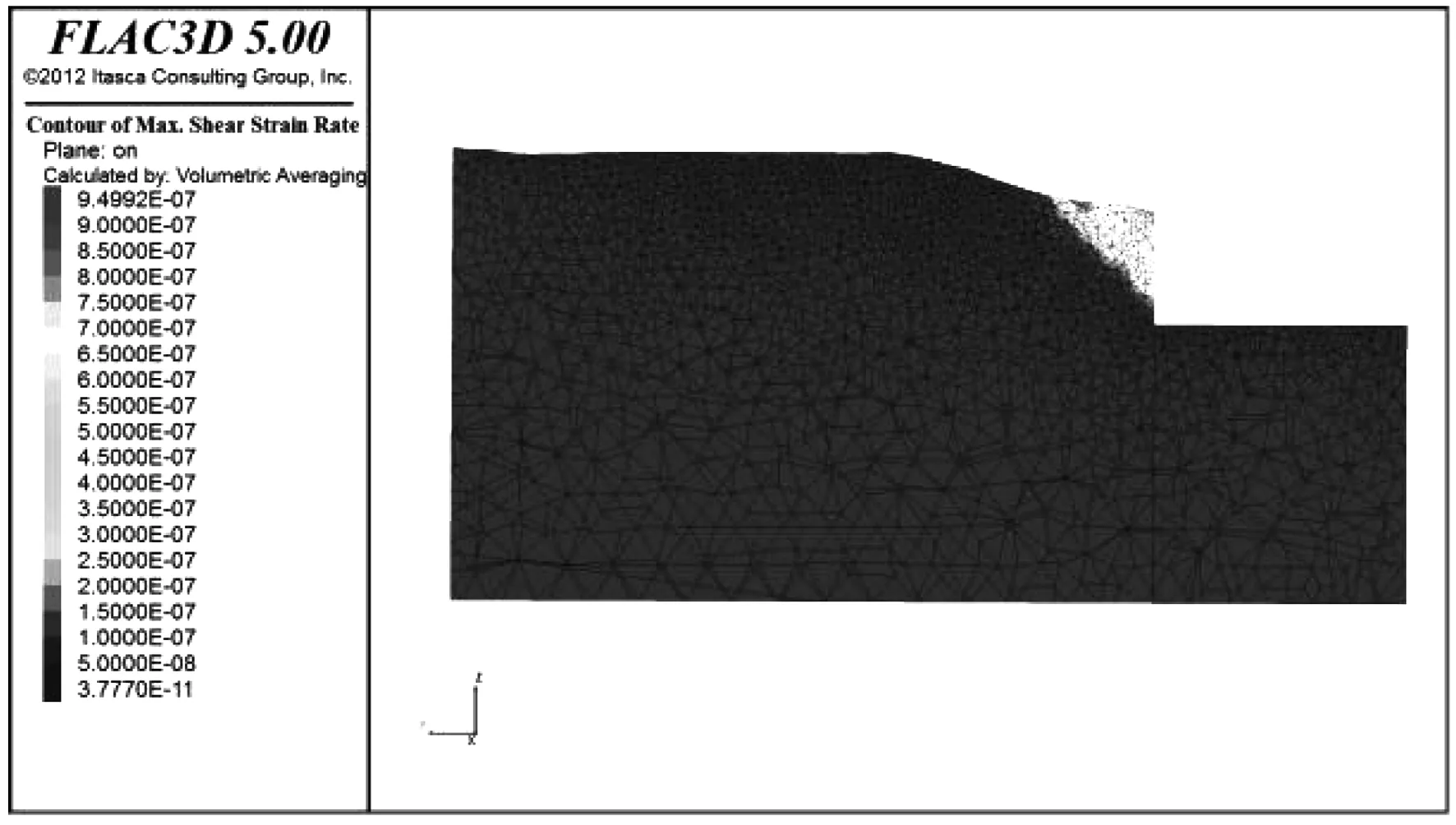
图20 Y方向最大剪应变云图Fig.20 Y direction max shear strain nephogram

图21 X方向塑性区分布云图Fig.21 X direction plastic zone distribution nephogram

图22 Y方向塑性区分布云图Fig.22 Y direction plastic zone distribution nephogram
4 结 论
由FLAC3D数值模拟软件做出的以上两种分别在自然工况和开挖工况的稳定性分析,得到以下结论:
1) 自然条件下斜坡处于一个稳定的状态。
2) 在该方案开挖条件下,边坡的位移量值非常大,边坡开挖,房屋的稳定性会受到极大的影响,容易造成房屋的开裂,建筑物发生拉裂缝,开挖线后20 m以及高程850.0 m以上的岩体都会因开挖受到非常大的影响,在此种方案下,边坡处于不稳定状态,极易产生失稳变形破坏。
