基于白河沟水利工程泄洪隧洞的水-力耦合模型研究

2018-10-16张开玉

水利科技与经济 2018年9期

张开玉

(贵州省水利水电勘测设计研究院，贵阳 550001)

1 工程背景

隧洞施工开挖是工程中存在较多安全问题的一个项目，主要因为其具有地质情况的不确定性，一是地下开挖过程常伴随着地下水位的变化；而且开挖过程中对山体围岩压力的卸荷导致山体应力重分布也会造成一系列的问题。常见的隧洞开挖问题为开挖过程中掌子面处出现突发性的涌水，这种工程灾害常影响隧洞结构稳定，形成施工现场的水量淤积，从而延误工期。

渗流是造成隧洞涌水的一个非常重要的原因，参数渗流量则是隧洞在设计和施工过程中所考虑到的一个关键参数[1]。在工程设计过程中，渗流量能够决定隧洞衬砌的整体型式，还会影响排水孔、灌浆深度、廊道布置等防渗措施的布置情况；在隧洞施工阶段，渗流量又会影响工程安排、工程安全措施等，并且影响工程进度；在隧洞工程竣工验收后的运营过程中，渗流量是评价工程安全、工程效益、环境影响情况等工程经济指标的重要参数[2-5]。因此，渗流量在隧洞工程中扮演着一个贯穿整个工程全过程的角色。近些年来，国内外众多学者及工程人员对渗流进行了大量的试验研究和现场研究等工作，但因为岩体本身所具有的不确定因素太多，以及隧洞开挖对围岩的影响较大，很难从系统上对渗流有准确的计算研究。目前，对于渗流计算尚未产生一套完整的理论以及公认计算方法，因此很难对其进行精确计算，只能根据工程实际情况进行针对性分析，从而得到渗流的计算方法。

盘县白河沟水利工程正常蓄水位1 840.00 m，正常蓄水位以下库容1 400×104m3，设计洪水位1 841.09 m，相应库容1 530×104m3，校核洪水位1 842.26 m，总库容1 670×104m3。兴利库容1 083×104m3，P=95%年供水量2 194×104m3。它的开工建设，对于进一步加快盘县水电资源开发、推进清洁可再生能源建设、促进县域经济社会发展具有重要意义。本文依托其右岸泄洪隧洞兼导流隧洞的开挖，通过数值模拟方法，对其不同开挖半径下的渗流情况进行研究，得到一种考虑工程所在地隧洞开挖半径和起始地下水位影响的渗流计算模型，对于工程防渗具有重要意义。

2 渗流场数值计算

2.1 边界条件

假设围岩为满足各向同性假设，地下水渗流过程为达西渗流，则计算参数、边界条件Darcy定律进行确定：

Qc/2πr=kcdh/dr

(1)

衬砌边界条件为：

h|r=r1=p1,h|r=r2=p2

(2)

由此可以得到能够流进衬砌里边的渗流量为：

(3)

考虑围岩范围内的情况：

Qr/2πr=krdh/dr

(4)

围岩边界条件为：

h|r=r2=p2,h|r=R=p3

(5)

由此可以得到能够流进围岩里边的渗流量为：

(6)

根据流入和流出衬砌的渗流量相等，得到：

(7)

式中：kr和kc分别为围岩和衬砌渗透系数；r1、r2分别为衬砌内径和衬砌外径；p1和p2分别为衬砌内外表面孔隙压力；R为远场半径，p3为远场水压。

围岩渗流解析图见图1。

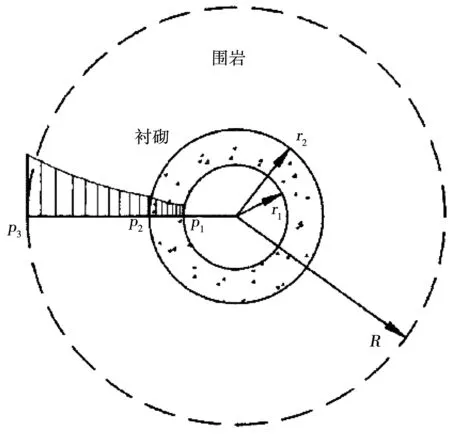
图1 围岩渗流解析图

2.2 渗流场计算结果

对于隧洞渗流计算，需要先对开挖过程的地下水位变化进行一定的分析。利用数值模拟方法，通过建立网格进行渗流有限元分析，建立地下水网格模型，模型所包括的横向范围是从洞室到左右50倍洞径，纵向范围为从洞室顶部一直到达地表。为了对渗流量在不同埋深下的影响进行分析，分别将隧洞的中心线一直到地下水位线所处的高度距离为20、30、40、50、100、150、200和300 m来进行计算，而其中的一些Darcy定律中的计算参数以及边界条件则根据现场资料而定。地下水位线网格图见图2。

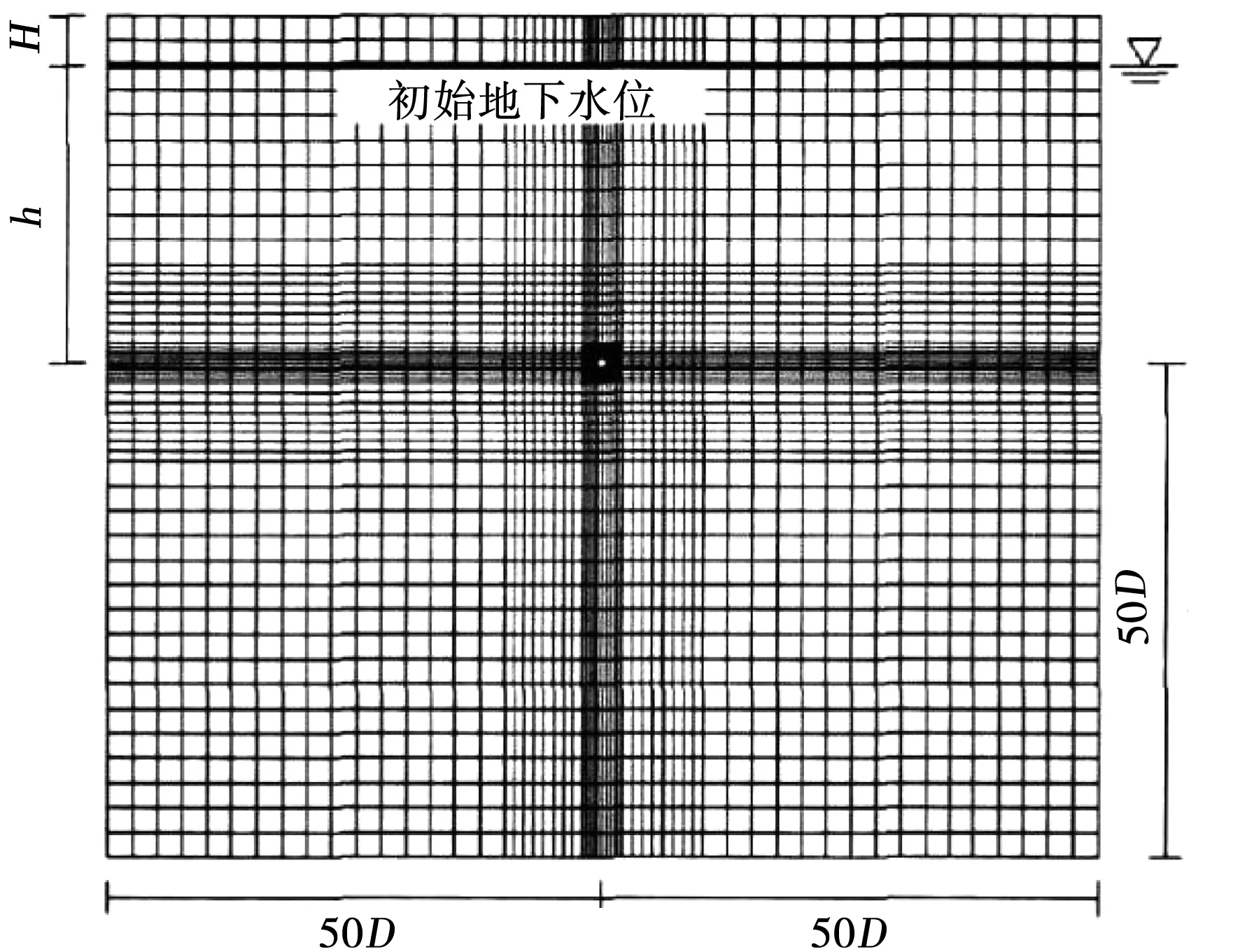
图2 地下水位线网格图

这里主要对隧洞的中心线一直到地下水位线所处高度距离为300 m的水平面为例进行分析，见图3。

图3 地下水位线变化模拟图

从图3可以明显看出，在隧道开始开挖进行的0.5 d、1 d、5 d、10 d和20 d，周围地下渗流场的孔压开始降低，并从中部向下凹陷，随着时间的推移，凹陷程度逐渐升高，到隧道完全开挖完成，临街面处的孔压已经降到0 MPa。此外，由于隧洞周围开挖排水对周围孔压产生一定的影响，使孔压急速下降，随着时间推移，下降的范围逐渐扩大，且孔压愈发减小。地下水位在此过程中也逐渐降低，在最初的0.5 d内，由于开挖时间较短，地下水位下降幅度为19.2 m，但是在开挖完成后的20 d内，地下水位的下降幅度已经达到79 m，所造成的地下水位变化是非常明显的。

3 开挖半径的影响分析

3.1 地下水位情况

为了考虑不同的埋深及隧洞开挖半径对于渗流的影响，需要先对开挖后过程中的地下水位下降过程进行分析，并根据不同隧洞开挖半径下的地下水位变化情况，对开挖过后的地下水位进行分析。这里主要分别对2.5、3.5、5和7.5 m的隧洞开挖半径下的情况进行分析，并取4种情况下的围岩的渗透系数分别为10-6、10-7、10-8和10-9m/s，隧洞的中心线一直到地下水位线所处的高度的距离与上文一致。

当隧洞的围岩渗透系数维持为10-7m/s的情况时，为了分析隧洞半径在渗流场上的一些影响，通过计算出2.5、3.5、5和7.5 m的隧洞开挖半径下的地下水位变化情况，并由之前的分析可知，对洞开挖后，地下水位将会下降，并在这种状态持续一段时间后恢复到稳定阶段。通过对渗流场稳定后的情况计算得到地下水位变化情况，见表1和图4。

表1 不同开挖半径下地下水位表

图4 开挖后地下水位与起始地下水位、开挖半径关系图

3.2 孔压情况

对于隧洞中心以上地下水位线不同高度的计算方案，整理开挖完成后20 d洞周垂直方向以及水平方向的孔压分布见图5。从图5可看出，不同计算方案下洞顶铅直方向上孔压分布规律基本一致，隧洞拱顶位置由于临空面排水作用，孔压为0 MPa。随着距顶拱铅直距离逐渐増大，洞顶孔压先迅速増大到最大值，之后孔压数值缓慢减小，在地下水位线浸润面处降低为零，在开挖完成后20 d，不同计算方案下地下水位线降低高度为55.6 m(h=100 m工况)至91 m(h=300 m工况)。

图5 不同埋深条件下隧洞垂直、水平孔压分布图

4 渗流模型分析

针对隧洞渗流量，将数值计算结果渗流场达到稳定后的数值解与解析解进行对比，选取Goodman[6]公式和Moon[7]公式作为参考，其中前者假定开挖过程中地下水位线保持不变，后者采用开挖降低后水位进行计算。在隧洞不同地下水位高度情况下，通过各种计算方法所得到的结果与数值解见图6。根据计算结果可以看出，当横坐标r/h从0.016 7逐渐增大至0.251 2时，隧洞埋深逐渐减小，3种计算方法得到的渗流量均逐渐减小。然而相比而言，Goodman公式计算结果最大，Moon公式结果最小，数值计算结果恰好处于两者包络线之间。这是由于在Goodman公式中，地下水位线假定保持初始状态不变，隧洞渗流场水力势一直相对较高，计算得到的渗流量较大；而在Moon公式中仅考虑开挖降低后水位，作用水头取为隧洞顶拱到降低后水位线的垂直最短距离，对于隧洞整个洞周而言渗透水力势偏小，该公式计算得到的渗流量较小，数值计算方法能够减少开挖降低后水位的影响，计算得到渗流量更为合理。