未知环境下移动机器人实时路径规划

张捍东，陈 阳，吴玉秀

安徽工业大学 电气与信息工程学院，安徽 马鞍山 243002

1 引言

移动机器人自主导航技术是移动机器人研究的重要分支之一，而路径规划是导航研究的一个重要环节，所谓路径规划是指在具有障碍物的环境中，按照一定的评价标准，寻找一条从起始状态到目标状态的无碰撞最优或次优路径[1]。

根据对环境信息的掌握程度可以将移动机器人路径规划问题分为全局路径规划和局部路径规划[2-3]。全局路径规划需要掌握所有的环境信息，根据所有的环境信息再进行路径规划，而局部路径规划只需掌握移动机器人当前可获取的环境信息。

快速扩展随机树（Rapidly-exploring Random Tree，RRT）算法[4]是近几年发展起来的基于采样的单查询路径规划方法，在处理非完整约束的路径规划问题时具有较大的优势。这种基于随机采样的运动规划方法由于其搜索方向的随机性，具有概率完备性，在有解的前提下，算法可获得可行解[5]。但由于该算法通常只能应用于已知环境中，所以环境信息获取时的计算量会很大[6]。

本文提出一种改进的RRT算法，该方法在滚动窗口内实现RRT算法，计算量大大减少；在随机环境中，机器人应用搭载的激光雷达，采集可调节滚动窗口内的环境信息，针对不同环境自主调整规划参数，实现随机环境中实时的路径规划。

2 RRT算法的基本原理

RRT算法在路径规划时以状态空间中的一个初始点作为根节点，通过随机采样增加叶节点的方式，生成一个随机扩展树。当随机树的叶节点包含目标点或目标区域时，从目标状态出发，找到父节点，依次进行，直至初始状态点，即可得到一条规划路径。

对移动机器人的工作空间（WorkSpace）进行环境建模，考虑轮式移动机器人的工作环境是二维工作空间W，且W∈R3，移动机器人的状态空间包含机器人的坐标位置和朝向角。基本的RRT算法描述[7-8]如下所示：首先将起点xinit放入随机树T中，作为根节点；在Wfree中随机选取一个位姿状态xrand；用Nearest_Neighbor()函数搜索树上距离xrand最近的扩展节点xnear；根据给定的标准选取输入u使得xnear尽可能接近xnew，反复调用函数EXTEND()，直到检测到障碍物为止，此时产生的一个新节点xnear被添加到树T上；选择新的随机状态xrand，重复执行上述算法，直至xnew=xgoal或xnew∈xgoal时，程序结束。

基本的RRT算法描述：

3 改进的RRT算法

3.1 基本原理

移动机器人实际工作环境是未知甚至复杂的，往往很难获取完整全局信息，且为了保证实时性，系统计算量不宜过大。针对上述问题，首先采用仅获取滚动窗口内环境信息的方法，因为RRT算法具有概率完备性，进而采用将RRT算法与滚动窗口相结合的方法，该方法通过分析滚动窗口内移动机器人上搭载的传感器探测到的环境信息结合RRT算法进行路径规划。考虑到某些环境下固定的窗口大小不能满足要求，本文提出了一种滚动窗口大小根据环境自适应调节的方法，并引入启发式估价函数，规划机器人从当前位姿到子目标点的路径，再控制移动机器人运动至子目标点。为了避免移动机器人运动到子目标点后陷入死锁，添加了一种动态监测机制，保证机器人到达合理的子目标点，重复上述过程，直至到达目标区域。

3.2 启发式估价函数的引入

类比A*算法[9-10]，为每个子节点x定义一个估价函数：表示从当前滚动窗口内的起始位姿到节点x的实际代价即实际路径长度，h(x)表示从节点x到目标xgoal的估计代价即启发式估价函数，令Dis(x1,x2)代表随机树中两个位姿节点间的欧几里得距离，取h(x)=Dis(x,xgoal)，x的节点选取满足使得f(x)最小。这样可以保证扩展树始终朝着目标点的方向生长，但是这可能会使得扩展树陷入局部最优，本文采用文献[11]提出的节点取消复原的方法来解决局部最优问题。主要思想是探索以前用过的空间是无用的，且易陷入局部最优。解决办法是生成新节点时，若xnew与父节点xnear的距离小于其与扩展树上的其他任何节点的距离，则将该节点加入扩展树。

3.3 滚动窗口的构建

移动机器人的实际工作环境往往是未知且复杂的，且对于实时性的要求高，所以全局路径规划往往是不可行的。

滚动规划算法主要包括：环境信息预测、局部滚动优化、反馈信息校正[12]。主要思路是将传感器可探测的环境作为当前窗口，在该窗口内进行路径规划，选取最优子目标点，找出起始位置到子目标点可行的局部路径，子目标点的选取方法将在下一小节说明。机器人运动过程中，每一个运动周期内的环境信息总在更新，从而将完整的规划路径分割成一步步的局部路径，与全局路径规划相比，计算量大大减小，可用于实时路径规划。

滚动窗口的选取过程如下：如图1所示，令机器人搭载激光雷达传感器的扫描半径为r，扫描区域为图1中View代表的区域即0～180°，直角坐标系表示当前时刻机器人的坐标系，朝向目标区域。

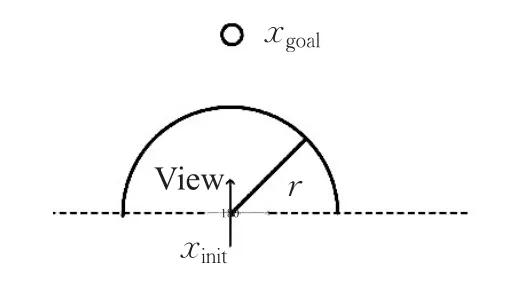
图1 滚动窗口示意图

3.4 子目标点的选取

当随机树在扩展过程中遇到障碍物时，为了使随机树快速成功地绕过障碍物，避免在局部复杂区域进行无效搜索，消耗迭代次数，这时就需要确定随机树的局部扩展方向[13-14]。如图2所示，Obs区域为工作空间中的障碍物区域，实际操作时将激光雷达扫描到的障碍物进行膨胀处理即可。膨胀处理后的障碍物如图2中Obs区域中用纯黑色区域表示，定义移动机器人当前位姿为滚动窗口圆心处S，目标区域中心G，为获取滚动窗口边界上的子目标点，定义子目标点为点P。有其中为定值与正相关，图2中取B为子目标点xsub。

图2 子目标点选取示意图

由于滚动窗口的状态空间采样次数和窗口大小有关，在不同的工作环境，应当配置不同的参数[15]，而实际的环境是未知的甚至是复杂的；如图3所示，移动机器人所处环境为通道环境且障碍物已经过膨胀处理，若采用原始半径为r的滚动窗口，则机器人前方0～180°滚动窗口边界无满足子目标点选取的xsub，从而使移动机器人陷入死锁。为解决该问题，本文提出一种滚动窗口大小自适应的方法，当局部环境中无障碍物，则子目标点为起始位姿和目标位姿连线与滚动窗口的交点，当局部环境类于图2。滚动窗口上存在xsub∈Wfree，通过计算筛选选取B为子目标点xsub，当局部环境如图3所示，半径为r的滚动窗口上不存在xsub，分析激光雷达获取的环境信息，取最大障碍距离dmax和最小障碍距离dmin，令新的滚动窗口半径为rnew=(dmax+dmin)/2，在新的滚动窗口中判断是否存在可行的子目标点xsub，若存在，xsub的选取类于图2的局部环境；否则，更新滚动窗口下dmax、dmin、rnew值，并继续上述判断过程。为了防止移动机器人从复杂环境逃离后一直以较小滚动窗口进行路径规划，从而导致系统效率过低，所以当移动机器人到达子目标点后需判断新的窗口环境，若新的窗口环境存在满足要求的子目标点xsub，则将已经更新了的rnew还原至初始值r，并继续上述判断过程。

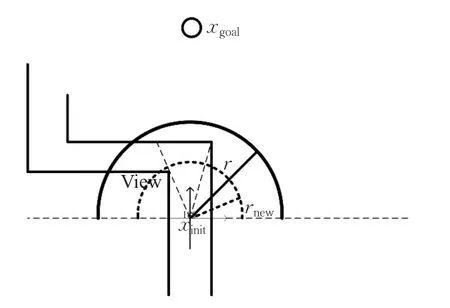
图3 复杂环境子目标点选取

3.5 动态监测机制的引入

当环境信息如图4所示，障碍物类似于图中Obs的凹型障碍，移动机器人的起始位姿xinit，起点为O，如图4所示的实线空心半圆，根据前文所述的子目标点选取策略，选取B为子目标点，若移动机器人运动至B点，考虑到实际所采用传感器的最小测量距离，此时机器人距离障碍物太近，导致传感器无法进行下一步规划，无法继续进行避障。为了解决该问题，引入了一种动态监测机制，当机器人位于起始点O，滚动窗口外的区域对于机器人而言为未知环境，此时规划路径时当作无障碍路径处理，B为子目标点，OB为路径规划方向，动态监测机制将在移动机器人运动的过程中监测事先规划好的路径，向未知区域延伸，并实时更新滚动窗口内的环境信息，若原路径方向出现障碍物，则重新选取子目标点，如图4所示，当机器人移动至点O1，滚动窗口更新为图中虚线空心圆，此时监测到原路径OB方向出现障碍物，重新选取子目标点，考虑在图4环境中启发式估价函数约束下RRT选取的随机性，假定选取右侧路径，更新后的环境信息类似于前文中图2所示环境；为了让机器人逃逸出这种陷阱环境，采取的方法是约束RRT的扩展范围，使其朝着临近障碍物的位置扩展，图4中线段L的方向为机器人大致的运动方向即当前时刻机器人的朝向；通过实验分析，在该类环境下还需考虑机器人逃逸出障碍时的朝向问题。在机器人实际运动过程中，对传感器采集到的环境中的障碍物进行膨胀处理。当机器人运动至点O2，此时滚动窗口边界与连续的障碍物存在交点，而当机器人运动至点O3，此时滚动窗口内的可视障碍物边界点为点E，点E位于滚动窗口内而非边界上，由于空间物体的连续性，可知此时障碍物的延伸方向为机器人当前坐标系下的O3S的左侧，控制机器人到达子目标点Ssub，滚动窗口环境如图5所示，分析机器人逃逸后的朝向问题。

图4 动态监测机制图示

图5 机器人朝向分析

图5 中，点S为滚动窗口内传感器可探测的最边界，根据前文所述的约束，控制子目标点到达膨胀处理后的点Ssub，此时机器人的View范围没有探测到障碍物，且考虑到障碍物边界的种类，大致可以分为如图5所示的m、n、k三种类型；为了保证机器人成功逃逸出陷阱环境，当机器人成功越过障碍物边界顶点E、点E1或点E3即可，采取的方法是：当机器人位姿从O3变为Ssub，即从窗口可探测到障碍物进入窗口无障碍物环境，此时RRT的扩展方向参考上一次规划的方向，即在当前机器人坐标系下的第二象限结合启发式估价函数在临近-x轴方向进行子目标点的选取。当目标位于机器人坐标系下前方区域，且滚动窗口View内在目标物方向有可行通道时，解除陷阱障碍逃逸约束。

成功越过障碍物边界顶点的可行性分析如下：

若障碍物边界的延伸方向为m、n、k，由于子目标点的选取在当前机器人坐标下的第二象限临近-x轴的方向，所以最多进行两次规划，规划的子目标点为Ssub1、Ssub2，此时O3SsubSsub1Ssub2组成的封闭几何图形近似为正方形，比值越小越接近正方形，rrobot表示机器人半径，且，则存在点Ssub2在O3S1上的投影可越过障碍物边界顶点。

3.6 步长的选取

随机树在扩展过程中，设定步长的不同会导致路径规划结果的不同，规划所消耗的时间也会不同。若步长太小，相应的扩展节点会增多，会导致处理时间增加，不利于系统的实时性要求，若步长太大，当机器人处于复杂环境下，可能不存在满足步长要求的随机点xnew，导致随机树重复搜索甚至陷入死锁[14]。为了满足实际需求，本文采用了一种变步长的方法。当搭载的传感器探测到局部环境中不存在障碍物时，则采用原始步长λ且采用贪婪法使得移动机器人向目标区域移动，当探测到的局部环境类似于前文图2所示，则选取步长为原始步长和滚动窗口半径二者取小，即λnew=min(λ,r)，当探测到的局部环境类似于前文图3所示，选取步长为原始步长和更新后的滚动窗口半径二者取小，即λnew=min(λ,rnew)。

3.7 算法的实现

综合前文所述，所提算法具体的实现步骤如下：

步骤1初始化，包括根据机器人的尺寸将获取的障碍物进行膨胀处理、移动机器人识别出目标机器人的位姿并朝向目标、全向激光雷达获取前方的环境信息，设置初始 r、λ(r＞λ)等。

步骤2判断滚动窗口边界是否存在可行的子目标点xsub，若存在，跳转至步骤3，否则跳转至步骤4。

步骤3在滚动窗口内的Wfree空间中随机选取一个状态xrand，并根据最短路径思想选取xnear，根据步长λ和节点取消复原方法确定xnew，跳转至步骤5。

步骤4 自适应调整λ、r为λnew、rnew，并跳转至步骤3。

步骤5判断扩展树是否到达子目标点，若到达，控制移动机器人输入（速度、角度）使得机器人朝向子目标点运动，动态监测规划的路径，若路径中无障碍物，跳转至步骤6，否则跳转至步骤3。

步骤6判断移动机器人是否到达目标区域xgoal，若到达，结束，否则跳转至步骤3。

4 实验

4.1 实验平台和实验环境

实验平台为HCR开源移动机器人机械套件和自主搭建的软硬件平台，采用的主控制器为嵌入式ARM开发板，主频1.6 GHz，如图6所示，该平台搭载全景视觉模块和激光雷达模块。实验环境为室外非强光环境。该平台搭载的激光雷达，扫描频率为6 Hz，精度为1°，可获取移动机器人前方0～180°区域的环境信息，该平台搭载了全景视觉模块，具有识别特定特征目标的能力，且可计算出目标相对于机器人当前位姿的坐标和角度，实验中将目标物用另外一台符合识别特征的机器人代替，期望的结果是移动机器人从起点出发，向目标机器人移动，且运动过程中仅通过分析滚动窗口内激光雷达获取的实时环境信息，结合算法进行路径规划，躲避环境中的障碍，并成功抵达目标区域。

图6 实验平台

将如图7的实验环境在移动机器人平台上处理后，环境显示如图8所示。可知，在当前窗口边界内激光雷达可探测到的环境是已知的，窗口外以及未探测到的环境是未知的，环境中激光雷达可探测到的障碍物（例如障碍物A）已进行了可视化标记处理，无法探测的信息（例如障碍物B）仅显示。

图7 实际的环境

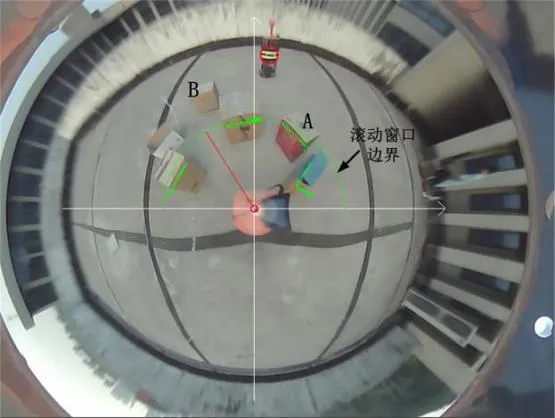
图8 处理后的环境信息显示

4.2 随机点状环境

当移动机器人处于如图9所示的随机点状环境中，针对两种算法分别进行了20次实验，图10给出了两种算法的路径规划过程，顺序为A-B-C-D。可知，在该环境下机器人在滚动窗口内根据约束条件自主实时规划可行的局部路径，控制机器人到达子目标点，并重复上述过程，最终到达目标区域；其中，实心圆为目标机器人，空心圆为目标区域，障碍物已经过膨胀处理；图11给出了二者实际路径结果对比，其中滚动RRT路径的平均路径长度为3 267 mm，所提算法的平均路径长度为3 228 mm。实验表明，所提算法和常规滚动RRT规划算法在随机点状环境中都可以实时规划路径，且规划的路径平均长度接近。

图9 随机点状实验环境

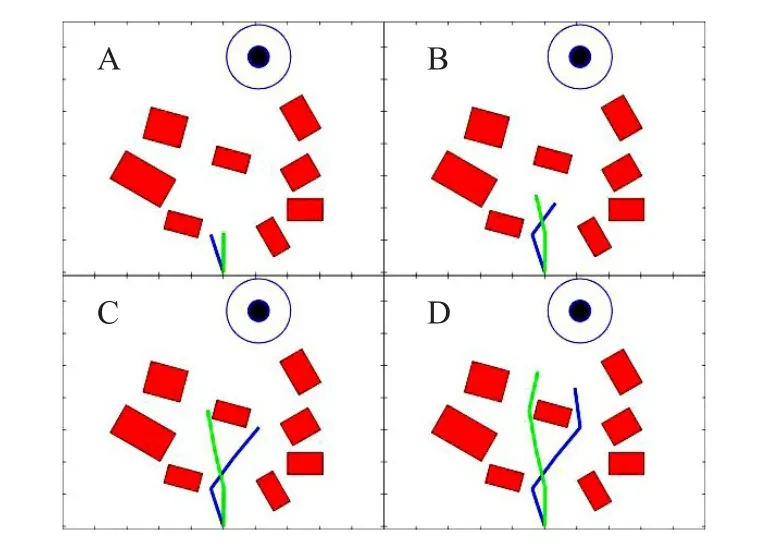
图10 随机点状环境下路径规划过程对比

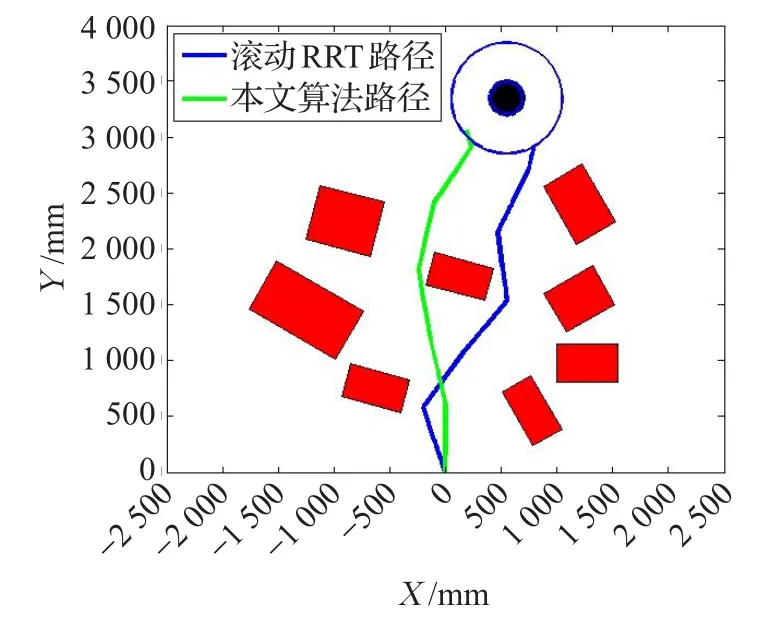
图11 随机点状环境下实际路径对比

4.3 通道环境

当移动机器人处于如图12所示的通道环境中，此时环境类似于图3所示。图13给出了两种算法的路径规划过程对比，顺序为A-B-C-D，其中虚线半圆为所提算法当前时刻滚动窗口大小，可知，在该环境下，由于传统滚动RRT算法滚动窗口半径固定，当机器人运动至A中的子目标点后会导致无法继续选取满足条件的子目标点，从而使移动机器人陷入死锁，而所提算法由于窗口半径可自适应调整，当机器人到达A中的子目标点后，自主调整窗口半径，使得移动机器人在窗口边界上可以找到满足条件的子目标点，由B、C可知调整后的滚动窗口避免机器人陷入死锁，由D可知机器人成功通过了该环境。图14给出了所提算法与滚动RRT算法实际路径的结果对比，其中，实心圆为目标机器人，空心圆为目标区域，障碍物已经过膨胀处理。实验结果表明所提算法在通道环境中可实时进行路径规划。

图12 通道实验环境

图13 通道环境下路径规划过程对比

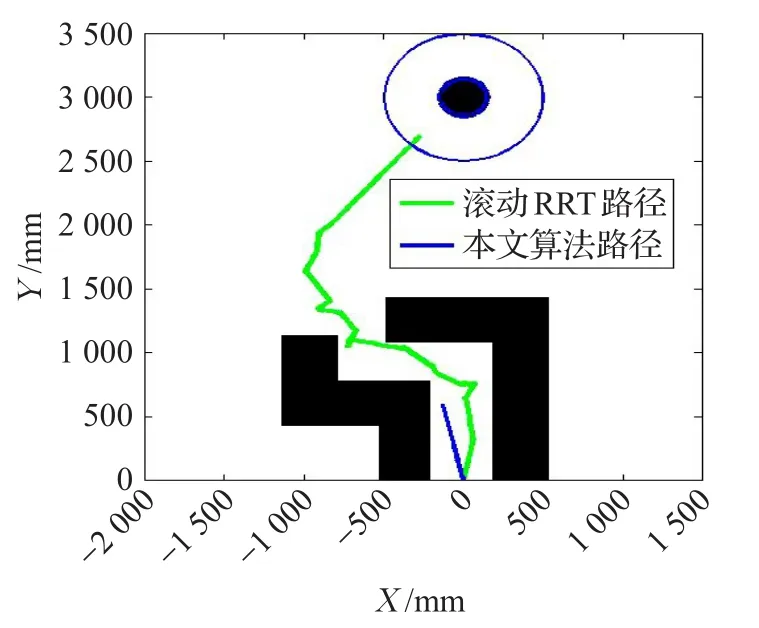
图14 通道环境下实际路径对比

4.4 陷阱环境

当移动机器人处于如图15所示的陷阱环境中，此时环境类似于图4所示。图16给出了两种算法的路径规划过程对比，顺序为A-B-C-D-E-F-G-H-I，可知，传统的滚动RRT算法在选取了当前环境下的子目标点后，由于窗口外的环境为未知环境，机器人运动至D中的子目标点后，由于此时视野域已被障碍物完全覆盖，无法进行下一步规划，从而使机器人陷入死锁。而所提算法中加入的动态监测机制，实时监测规划好的路径，在机器人向B和C中的子目标点运动的过程中，监测到原路径不可行，重新规划路径，根据前文所述的约束，机器人在D、E、F中沿着障碍物前进，在G、H中成功越过了障碍，逃逸成功后在i中解除约束。图17给出了所提算法与滚动RRT算法实际路径规划的结果对比，其中，实心圆为目标机器人，空心圆为目标区域，障碍物已经过膨胀处理。实验结果表明所提算法在陷阱环境中可实时进行路径规划，且可逃逸出该障碍环境并成功抵达目标区域。

图15 陷阱实验环境

图16 陷阱环境下路径规划过程对比

图17 陷阱环境下实际路径对比

5 结束语

本文分析了基本的RRT算法，将基本RRT与自适应滚动窗口相结合，并加入了动态监测机制，用于实时监测规划好的路径，将该方法应用于未知环境下的移动机器人实时的路径规划。通过对大量实验的结果对比分析，表明该方法可以满足实时路径规划的需求，在随机点状环境中所提算法和滚动RRT的效果比较接近，在通道环境下，固定窗口半径的滚动RRT算法相较与所提算法易陷入死锁，在类似于凹型陷阱环境下，所提算法加入的动态监测机制，可以使得移动机器人逃逸出陷阱并成功抵达目标区域，避免陷入死锁。由于机器人在运动过程中对规划好的路径是实时监测的，当监测到原规划路径时可行变为不可行，则进行重新规划，该过程为实时的，因此本文算法对于动态环境下的机器人实时路径规划同样具有一定的实用性和有效性。