分布式驱动电动车电机失效后行驶稳定性研究

刘雨晖，陈光耀，冉 渊，李 涛

(武汉理工大学 汽车工程学院，湖北 武汉 430070)

鉴于分布式驱动电动车具有底盘空间大、传动效率高、动力经济性好、操纵稳定性突出等优势[1-2]，目前已成为电动汽车研发领域的重点研究对象[3-4]。分布式驱动电动车车身稳定控制、横摆力矩控制研究是保障车辆安全行驶的关键因素[5-11]。在分布式驱动电动车行驶稳定性研究方面，针对电机失效后的行驶稳定性研究较少。电机失效后仍具有良好的行驶稳定性是保证行车安全的关键。因此，分布式驱动电动车电机失效后行驶稳定性的研究，对降低行车隐患有着重要意义。

笔者提出了一种电机失效安全控制策略，针对分布式驱动电动车直线高速行驶时的电机失效情况，提供了相应的控制方案，提高电机失效后的行驶稳定性。采用CarSim和MATLAB/Simulink联合仿真的方式对安全控制策略干预和不干预电机失效过程进行仿真实验并对仿真结果进行分析。

1 分布式驱动电动车动力学模型

CarSim软件提供大量具有准确参数的模型库以及MATLAB/Simulink软件图形化编程提供动态系统建模、仿真、分析集成环境，笔者采用CarSim和MATLAB/Simulink联合仿真的方式建立分布式驱动电动车整车动力学模型并对电机失效过程进行仿真。采用CarSim软件建立整车模型中车体、空气动力学、制动系统、悬架系统、轮胎模型，采用MATLAB/Simulink软件建立电机模型，通过CarSim和MATLAB/Simulink联合仿真实现分布式驱动的效果。

永磁同步电机具有转矩密度高、转矩脉动低、振动噪声小、过载能力强等优点，被广泛用作电动汽车驱动电机。笔者采用永磁同步电机作为分布式驱动电动车的驱动电机。利用MATLAB/Simulink软件建立用于分布式驱动电动车电机失效仿真的三相永磁同步电机矢量控制系统模型，如图1所示。

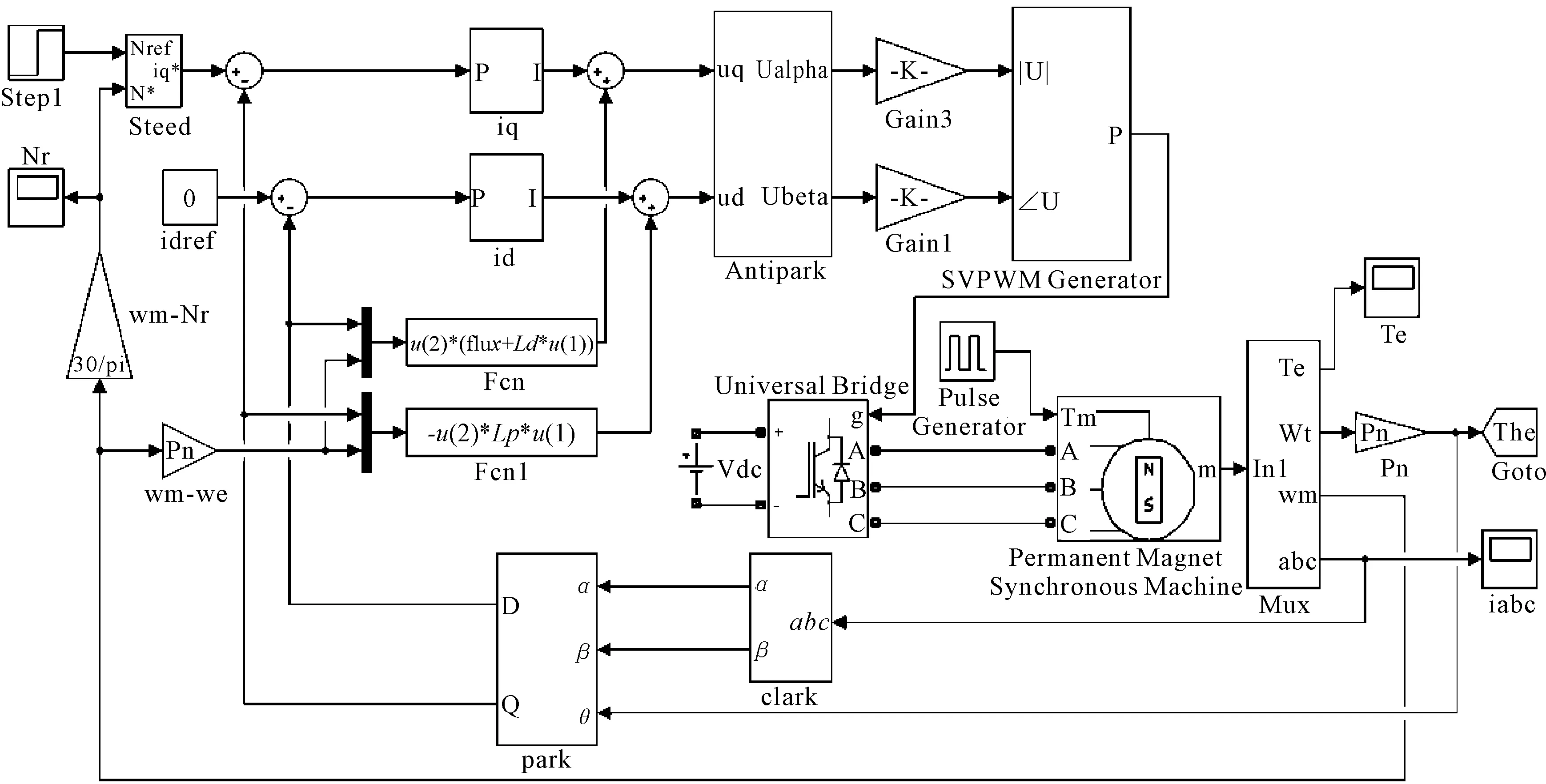
图1 三相永磁同步电机矢量控制系统模型

2 电机失效后行驶稳定性仿真分析

2.1 单电机失效的仿真分析

单电机失效包括：左前、右前、左后、右后轮失效4种情况。笔者对分布式驱动电动车直线高速行驶电机失效后行驶稳定性进行分析时，左前、右前轮失效视为同种情况，左后、右后轮失效视为同种情况。笔者选取左前和右后轮失效情况进行分析，单电机失效后各行驶稳定性指标变化曲线如图2所示。

图2 单电机失效后各行驶稳定性指标变化曲线

由图2(a)可知，1 s时左前轮失效，1～1.2 s横摆角速度激增至0.35 deg/s，1.2～1.5 s回落至0.17 deg/s，1.5～1.7 s缓升至0.21 deg/s，1.7～5 s稳定在0.21 deg/s附近。1 s时右后轮失效，1～1.2 s横摆角速度激增至0.18 deg/s(绝对值)，1.2～1.5 s回落至0.09 deg/s(绝对值)，1.5～1.8 s缓升至0.11 deg/s(绝对值)，1.8～5 s稳定在0.11 deg/s(绝对值)附近。

由图2(b)可知，1 s时左前轮失效，1～1.3 s质心侧偏角激增至0.043°(绝对值)，1.3～1.6 s回落至0.035°(绝对值)，1.6～1.9 s缓升至0.036°(绝对值)，1.9～5 s稳定在0.036°(绝对值)附近。1 s时右后轮失效，1～1.3 s质心侧偏角激增至0.025°，1.3～1.6 s回落至0.02°，1.5～1.8 s缓升至0.021°，1.8～5 s稳定在0.021°附近。

由图2(c)可知，1 s时左前轮失效，1～1.3 s侧向加速度激增至0.13 m/ s2，1.3～5 s在0.11 m/s2上下浮动，最大值达到0.15 m/s2。1 s时右后轮失效，1～1.3 s侧向加速度激增至0.074 m/s2(绝对值)，1.3～5 s在0.055 m/s2(绝对值)上下浮动，最大值达到0.093 m/s2(绝对值)。

由图2(d)可知，1 s时左前轮失效，车辆向左偏移，1～5 s最大侧向位移为0.86 m。1 s时右后轮失效，车辆向右偏移，1～5 s最大侧向位移为0.42 m(绝对值)。

2.2 双电机失效的仿真分析

双电机失效包括：同轴、异轴对侧、异轴同侧双电机失效。笔者选取左前右前轮失效、左前右后轮失效、右前右后轮失效进行分析，双电机失效后各行驶稳定性指标变化曲线如图3所示。

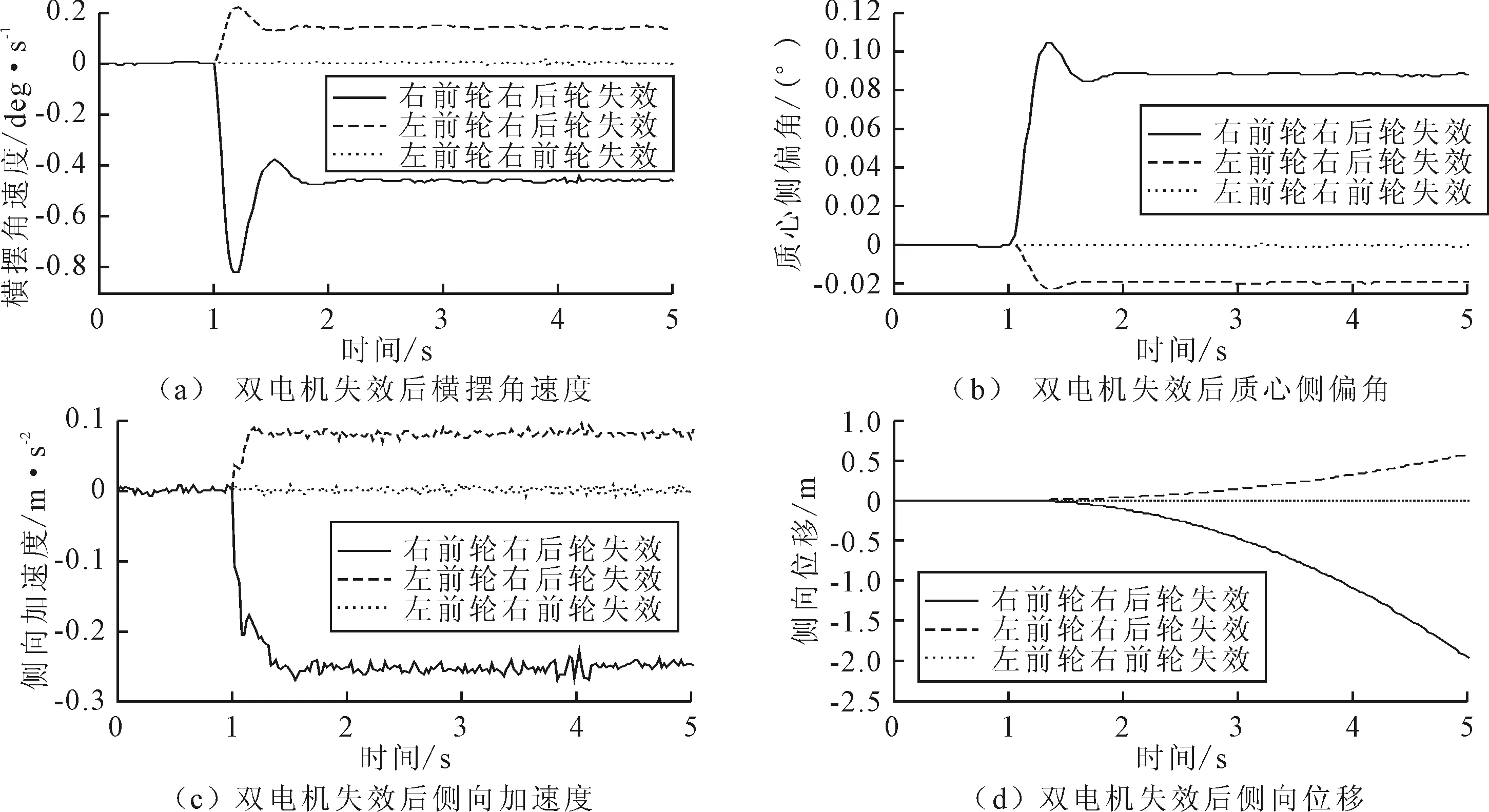
图3 双电机失效后各行驶稳定性指标变化曲线

由图3(a)可知，1 s时同轴双电机失效，1～5 s横摆角速度在0 deg/s上下波动。1 s时异轴对侧双电机失效，1～1.2 s横摆角速度激增至0.82 deg/s(绝对值)，1.2～1.5 s回落至0.38 deg/s(绝对值)，1.5～1.7 s缓升至0.47 deg/s(绝对值)，1.7～5 s稳定在0.47 deg/s(绝对值)附近。1 s时异轴同侧双电机失效，1～1.2 s横摆角速度激增至0.22 deg/s，1.2～1.5 s回落至0.12 deg/s，1.5～1.7 s缓升，1.7～5 s稳定在0.14 deg/s附近。

由图3(b)可知，1 s时同轴双电机失效，1～5 s质心侧偏角在0°上下波动。1 s时异轴对侧双电机失效，1～1.4 s质心侧偏角激增至0.10°，1.4～1.8 s回落至0.086°，1.8～5 s略微缓升。1 s时异轴同侧双电机失效，1～1.4 s质心侧偏角激增至0.023°(绝对值)，1.4～1.7 s回落至0.019°(绝对值)，1.7～5 s趋于稳定。

由图3(c)可知，1 s时同轴双电机失效，1～5 s

侧向加速度在0 m/s2上下波动。1 s时异轴对侧双电机失效，1～1.5 s侧向加速度激增至0.27 m/s2(绝对值)，1.5～5 s在0.25 m/s2(绝对值)上下浮动。1 s时异轴同侧失效，1～1.3 s侧向加速度激增至0.082 m/s2，1.3～5 s在0.079 m/s2上下浮动，最大值达到0.093 m/s2。

由图3(d)可知，1 s时同轴双电机失效，侧向位移在0 m上下波动。1 s时异轴对侧双电机失效，车辆向右偏移，最大侧向位移为1.97 m(绝对值)。1 s时异轴同侧双电机失效，车辆向左偏移，最大侧向位移为0.57 m。

2.3 三电机失效的仿真分析

三电机失效包括：仅左/右前轮未失效、仅左/右后轮未失效。笔者选取右前轮左后轮右后轮失效、左前轮右前轮左后轮失效进行分析，三电机失效后各项行驶稳定性指标变化曲线如图4所示。

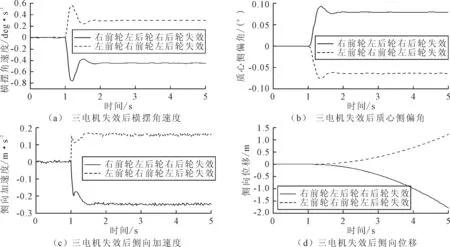
图4 三电机失效后各行驶稳定性指标变化曲线

由图4(a)可知，1 s时左前轮右前轮左后轮失效，1～1.2 s横摆角速度激增至0.56 deg/s，1.2～1.5 s回落至0.24 deg/s，1.5～1.8 s缓升至0.31 deg/s，1.8～5 s之间稳定在0.31 deg/s附近。1 s时右前轮左后轮右后轮失效，1～1.2 s横摆角速度激增至0.76 deg/s(绝对值)，1.2～1.8 s回落至0.38 deg/s(绝对值)，1.8～5 s缓升至0.45 deg/s(绝对值)趋于稳定。

由图4(b)可知，1 s时左前轮右前轮左后轮失效，1～1.3 s质心侧偏角激增至0.076°(绝对值)，1.3～1.6 s回落至0.061°(绝对值)，1.6～1.9 s缓升至0.062°(绝对值)，1.9～5 s稳定在0.062°(绝对值)附近。1 s时右前轮左后轮右后轮失效，1～1.3 s质心侧偏角激增至0.093°，1.3～1.6 s回落至0.076°，1.5～1.8 s缓升至0.079°，1.8～5 s稳定在0.079°附近。

由图4(c)可知，1 s时左前轮右前轮左后轮失效，1～1.4 s侧向加速度激增至0.17 m/s2，1.3～5 s在0.16 m/s2上下浮动，最大值为0.17 m/s2。1 s时右前轮左后轮右后轮失效，1～1.4 s侧向加速度激增至0.26 m/s2(绝对值)，1.3～5 s在0.24 m/s2(绝对值)上下浮动，最大值为0.26 m/s2(绝对值)。

由图4(d)可知，1 s时左前轮右前轮左后轮失效，车辆向左偏移，最大侧向位移为1.2 m。1 s时右前轮左后轮右后轮失效，车辆向右偏移，最大侧向位移为1.8 m(绝对值)。

综上所述，同轴双电机失效对行驶稳定性影响不大。单电机、异轴对侧和异轴同侧双电机、三电机失效，车辆两侧驱动力矩不同，产生非期望横摆力矩导致横摆角速度、质心侧偏角激增，侧向加速度、侧向位移增加。悬架的动态特性和轮胎的侧向弹性使得横摆角速度、质心侧偏角和侧向加速度达到峰值后回落，最终趋于稳定。

3 电机失效安全控制策略及仿真研究

3.1 控制规则

笔者提出了一种电机失效安全控制策略，采用关闭一个或多个电机的方法保证行驶稳定性。电机失效安全控制策略根据不同失效情况实施相应控制方案。电机失效安全控制策略如表1所示。

表1 电机失效安全控制策略

3.2 电机失效安全控制策略仿真验证

3.2.1 单电机失效的控制策略和仿真

通过仿真分析可得单电机失效后电机失效安全控制策略干预和不干预失效过程的各行驶稳定性指标变化曲线，如图5所示。

图5 单电机失效控制

由图5(a)～图5(d)可知，1 s时单电机失效，横摆角速度在1～1.1 s激增至峰值，其峰值约为电机失效安全控制策略未干预时峰值的1/10，1.1～1.2 s迅速回落，1.2～1.3 s趋于稳定，1.3～5 s稳定在0 deg/s附近；质心侧偏角在1～1.2 s激增至峰值，其峰值约为电机失效安全控制策略未干预时峰值的1/20，1.2～1.3 s开始回落，1.3～2 s趋于稳定，2～5 s稳定在0°附近；侧向加速度1～1.1 s达到峰值并做锯齿形波动，其峰值约为电机失效安全控制策略未干预时峰值的1/5，1.3～5 s在0 m/s2上下做小幅度锯齿状浮动；1 s时单电机失效，侧向位移基本保持在0 m的稳定状态。

3.2.2 双电机失效的控制策略和仿真

通过仿真分析可得双电机失效后电机失效安全控制策略干预和不干预失效过程的各行驶稳定性指标变化曲线，如图6所示。

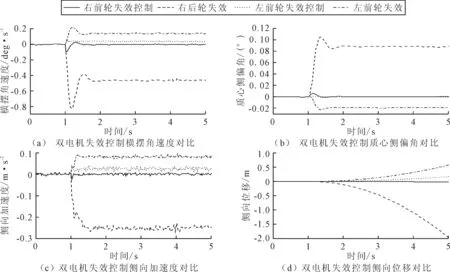
图6 双电机失效控制

由图6(a)可知，1 s时异轴异侧电机失效，横摆角速度在1～1.05 s激增至峰值0.058 deg/s，其峰值约为电机失效安全控制策略未干预时峰值的1/4，1.05～1.1 s回落至0.028 deg/s，1.1～1.7 s缓升并趋于稳定，1.7～5 s趋于稳定，其稳定值约为电机失效安全控制策略未干预时峰值的1/4。1 s时异轴同侧电机失效，采取关闭对侧电机的方式，车辆完全失去动力，横摆角速度在1～1.5 s存在一次明显波动，1.5～5 s趋于稳定值0 deg/s。

由图6(b)可知，1 s时异轴异侧电机失效，质心侧偏角在1～5 s基本维持在0°的稳定状态。1 s时异轴同侧电机失效，采取关闭对侧电机的方式，质心侧偏角在1～1.5 s之间存在一次明显波动，在1.5～5 s之间趋于稳定值0°。

由图6(c)可知，1 s时异轴异侧电机失效，侧向加速度在1～1.025 s达到峰值0.003 6 m/s2，其峰值约为电机失效安全控制策略未干预时峰值的1/2，1.3～5 s趋于稳定，其稳定值约为电机失效安全控制策略未干预时稳定值的1/2。1 s时异轴同侧电机失效，采取关闭对侧电机的方式，侧向加速度在1～1.05 s存在一次明显波动，1.5～5 s趋于稳定值0 m/s2。

由图6(d)可知，1 s时异轴异侧电机失效，车辆向左偏移，最大侧向位移为0.17 m，其峰值约为电机失效安全控制策略未干预时峰值的1/3。1 s时异轴同侧电机失效，采取关闭对侧电机的方式，侧向位移1～1.5 s存在一次明显波动，1.5～5 s趋于稳定值0 m。

3.2.3 三电机失效的控制策略和仿真

通过仿真分析可得三电机失效后电机失效安全控制策略干预和不干预失效过程的各行驶稳定性指标变化曲线，如图7所示。

由图7(a)～图7(d)可知，1 s时三电机失效，横摆角速度在1～1.5 s激增至峰值并迅速回落趋于稳定，1.5～5 s维持在0 deg/s附近；质心侧偏角在1～1.5 s激增至峰值并迅速回落趋于稳定，1.5～5 s维持在0°附近；侧向加速度在1～1.05 s激增至峰值并迅速回落趋于稳定，1.05～5 s维持在0 m/s2附近；侧向位移基本保持在0 m的稳定状态。

综上所述，电机失效安全控制策略干预电机失效过程，横摆角速度、质心侧偏角和侧向加速度的峰值明显减小，稳定后波动幅度降低，侧向位移基本不变。异轴异侧电机失效后，横摆角速度、侧向加速度和侧向位移的峰值和稳定值降低但仍存在不稳定倾向，质心侧偏角在0°附近波动。异轴同侧电机、三电机失效后，电机失效安全控制策略为保证行车安全关闭正常电机，车辆完全失去动力，各项指标最后均稳定在零值附近。电机失效安全控制策略干预电机失效过程能够对行驶稳定性4项指标进行控制，有效提高电机失效后的行驶稳定性。

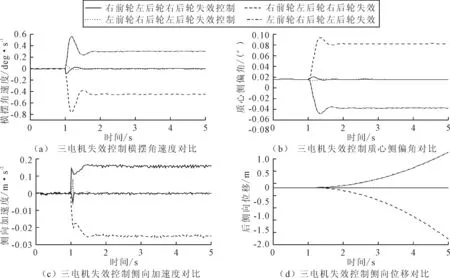
图7 三电机失效控制

4 结论

分布式驱动电动车直线高速行驶时，电机失效会引起行驶稳定相关性指标大幅波动，存在行车隐患。笔者提出的电机失效安全控制策略根据不同电机失效情况，提供不同控制方案，能够改善电机失效初期引起的横摆角速度、质心侧偏角和侧向加速度的短时激增，降低以上3项指标稳定后的幅值，缩短电机失效后相同时间内侧向位移大小，提高行驶稳定性。