减振器阻尼非线性对汽车平顺性影响分析
2018-10-15王丽红
吴 波,王丽红
(武汉理工大学 机电工程学院,湖北 武汉 430070)
悬架系统是影响车辆舒适性、操纵稳定性、安全性的关键总成之一,目前针对线性悬架系统的研究比较多,但在非线性方面还没有很成熟的理论[1]。汽车悬架总成是一个复杂的非线性系统,也正是这些非线性特性,极大地改善了汽车的性能。因此在进行整车性能仿真时,建立各个环节准确的非线性模型显得十分必要[2-3]。在以往的研究中,大部分学者都是建立最基本的七自由度整车平顺性模型,忽略了不同车型之间的差异,如以往的大多数模型都忽略了人椅系统,而不同位置的人椅系统对路面激励的响应不同[4],导致仿真结果存在较大误差;或者在以整车数学模型为基础研究悬架时,用理论公式而非用实验数据表示其非线性特性,降低了仿真分析的准确性[5-6]。随着计算机仿真技术的快速发展及动力学理论的不断完善,理论模型更接近真实系统,但也意味着计算中需要识别的参数更多,求解更麻烦。因此根据现代汽车的特点,建立更为准确的系统动态模型,将实验数据与理论模型相结合,为汽车研发提供更有力的依据,是研究者们共同的目标。笔者将某跨界车简化成十二自由度模型,考虑了人椅系统对激励的响应,从减振器的阻尼-速度特性实验数据着手,建立阻尼器的非线性特性模型,并分析其对整车性能的影响。
1 系统模型的建立
1.1 跨界车十二自由度动力学模型
汽车是由悬架、车身、轮胎、人椅系统等组成的复杂的振动系统,各子系统之间的相互约束及路面激励都影响着车辆的平顺性,故建立了图1所示的跨界车十二自由度模型,其中包括车身的垂向、俯仰和侧倾3个自由度,轮胎垂直方向的4个自由度以及人椅系统垂直方向的5个自由度。
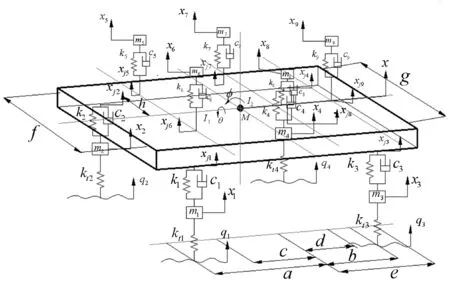
图1 跨界车动力学模型简图
对跨界车整车做如下假设:
(1)忽略轮胎阻尼对整车性能的影响;
(2)在车辆满载时,将人和座椅看作一个整体,其中第三排人椅系统包含3个人,在分析时考虑人椅系统的刚度、阻尼;
(3)将车身视为具有集中质量的刚体。其中,mi(i=1,2,…,4)为非簧载质量;Mi(i=1,2,…,5)为人椅系统质量;ki和ci(i=1,2,…,4)分别为悬架等效刚度和阻尼系数;Ki和Ci(i=1,2,…,5)分别为人椅系统等效刚度和阻尼系数;kti为轮胎等效刚度系数;qi为四轮路面输入;xi(i=1,2,…,4)为非簧载质量位移;Xi(i=1,2,…,5)为人椅系统位移;xji和Xji分别为车身连接悬架系统及人椅系统处的位移;M为车身质量;x为质心处位移;θ和φ分别为车辆侧倾运动和俯仰运动的角度;I1和I2分别为侧倾运动和俯仰运动的转动惯量;a和b分别为前后轴距质心距离;c、d、e分别为前中后排人椅距质心距离;f、g分别为前轮距和后轮距;h为左右人椅距中轴距离。
1.2 系统数学模型
当悬架、人椅系统、轮胎等子系统刚度与阻尼为线性时,根据图1所示模型中各系统之间的关系,可得整车模型的动力学方程为:
(1)
式中:Fti分别为4个轮胎的垂向力;Fsi分别为4个悬架的垂向力(弹簧力和阻尼力的合力);FSi分别为5个人椅系统的垂向力(弹簧力和阻尼力的合力),其计算式为:
(2)
1.3 建立非线性减振器模型
十二自由度线性模型虽考虑人椅系统对激励的响应,便于汽车平顺性分析,但忽略了悬架系统的非线性环节(如减振器非线性)对平顺性的影响。根据图2所示的某公司实测跨界车后独立悬架阻尼特性参数曲线,建立减振器非线性模型,并嵌入到传统的线型模型中。
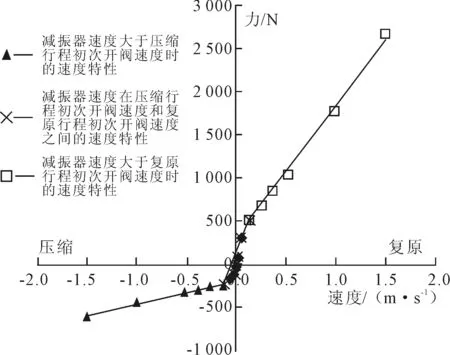
图2 减振器特性参数实验数据拟合曲线
根据实验数据的特点,为准确反映模型的响应特性,采用分段线性的方法进行拟合,以减振器的初次开阀速度vki(i=f,y分别代表复原行程和压缩行程)为分界点[7],每一段的斜率即该速度范围内的阻尼系数为C1i(i=1,2,3)。
通过拟合,后悬架减振器阻尼系数为:
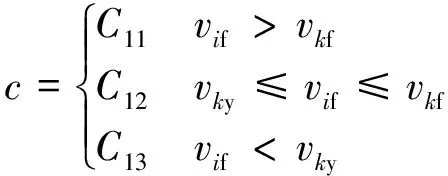
(3)
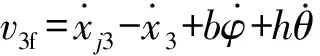
2 路面激励时域模型
路面激励作为车辆行驶过程中最基本的振动输入信号,选择合适的模拟方法,建立准确的路面模型,对于研究车辆平顺性、操纵稳定性尤为重要。为了更接近实际情况,故考虑了左右车轮轨迹的相干性和前后车轮轨迹的迟滞性,利用白噪声滤波法建立路面激励时域模型。
其中,路面功率谱为:
(4)
式中:Gs(n0)为路面不平度系数;n0为参考空间频率,n0=0.1;n为空间频率。
路面不平度对单个轮胎产生的激励模型[8]可以表示为:
(5)
式中:n1为道路空间截止频率,n1=0.011;u为跨界车行驶速度;w(t)为白噪声激励;q(t)为路面不平度激励模型。
考虑左、右轮迹的相干性,可将其看作是由两个不相关的单位白噪声的双输入线性系统响应[9],而汽车等速直线行驶时,前轮的路面激励qf和后轮路面激励qr是相同的,只不过存在一个滞后时间τ[10]。其中τ=(a+b)/u,则前、后轮路面激励关系为:
qr(t)=qf(t-τ)
(6)
利用滤波白噪声法,对车速为60 km/h,B级路面不平度时四轮激励时域模拟信号进行模拟,结果如图3和图4所示。
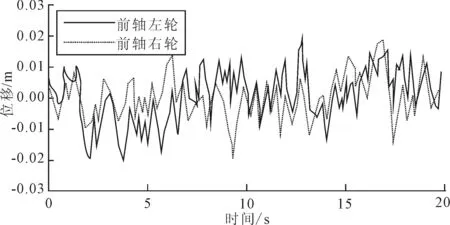
图3 跨界车前轴左轮和右轮路面激励
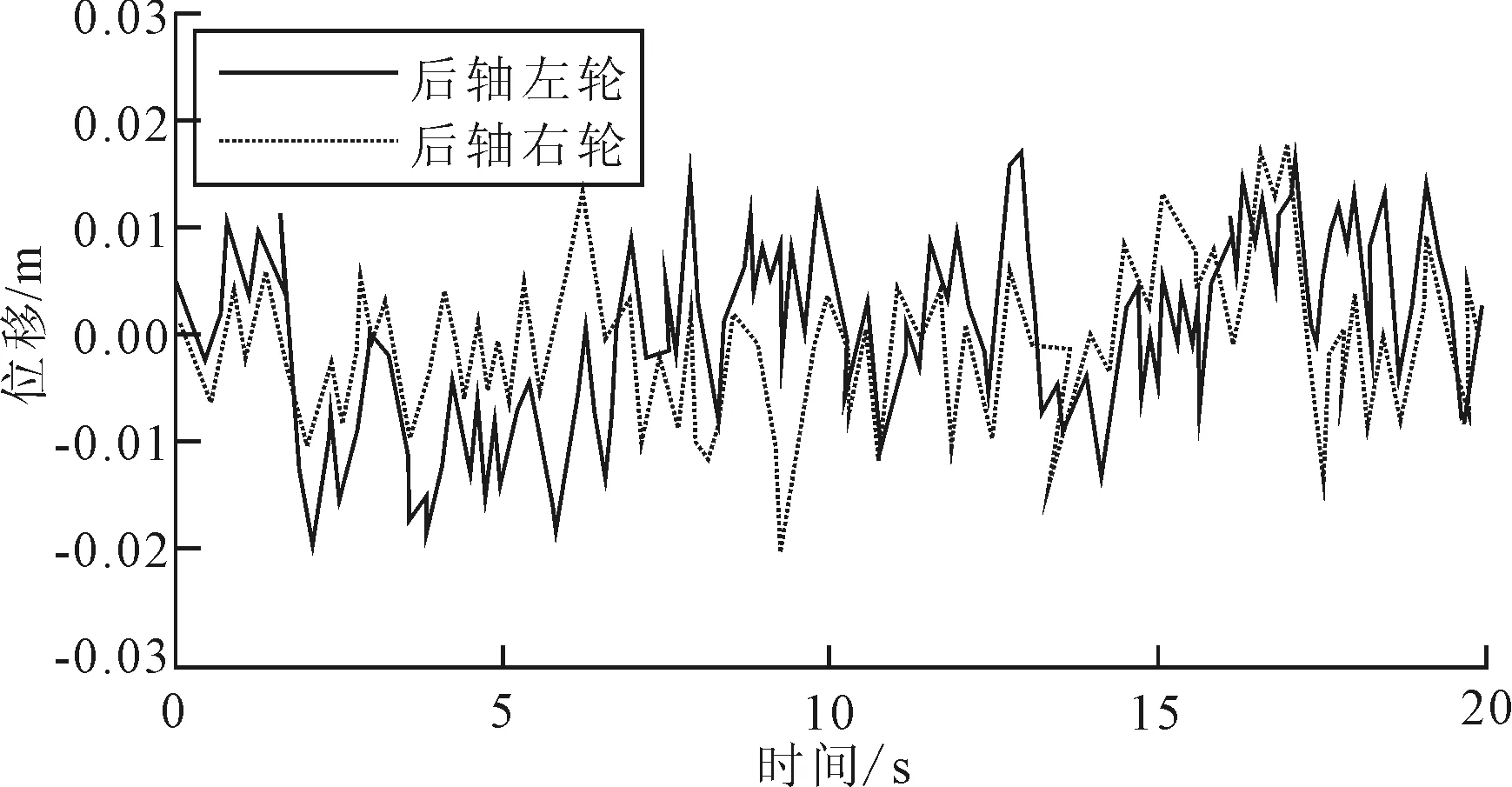
图4 跨界车后轴左轮和右轮路面激励
3 仿真结果及分析
根据已建立的整车数学模型和路面激励时域模型,利用MATLAB中的Simulink工具箱搭建整车动力学仿真计算模型,输入已知的整车参数,采用变步长Ode45求解器进行求解,以保证足够的精度。
3.1 线性模型仿真结果
结合上文中建立的整车动力学方程及路面不平度模型,利用Simulink进行仿真分析,结果如图5~图6所示。
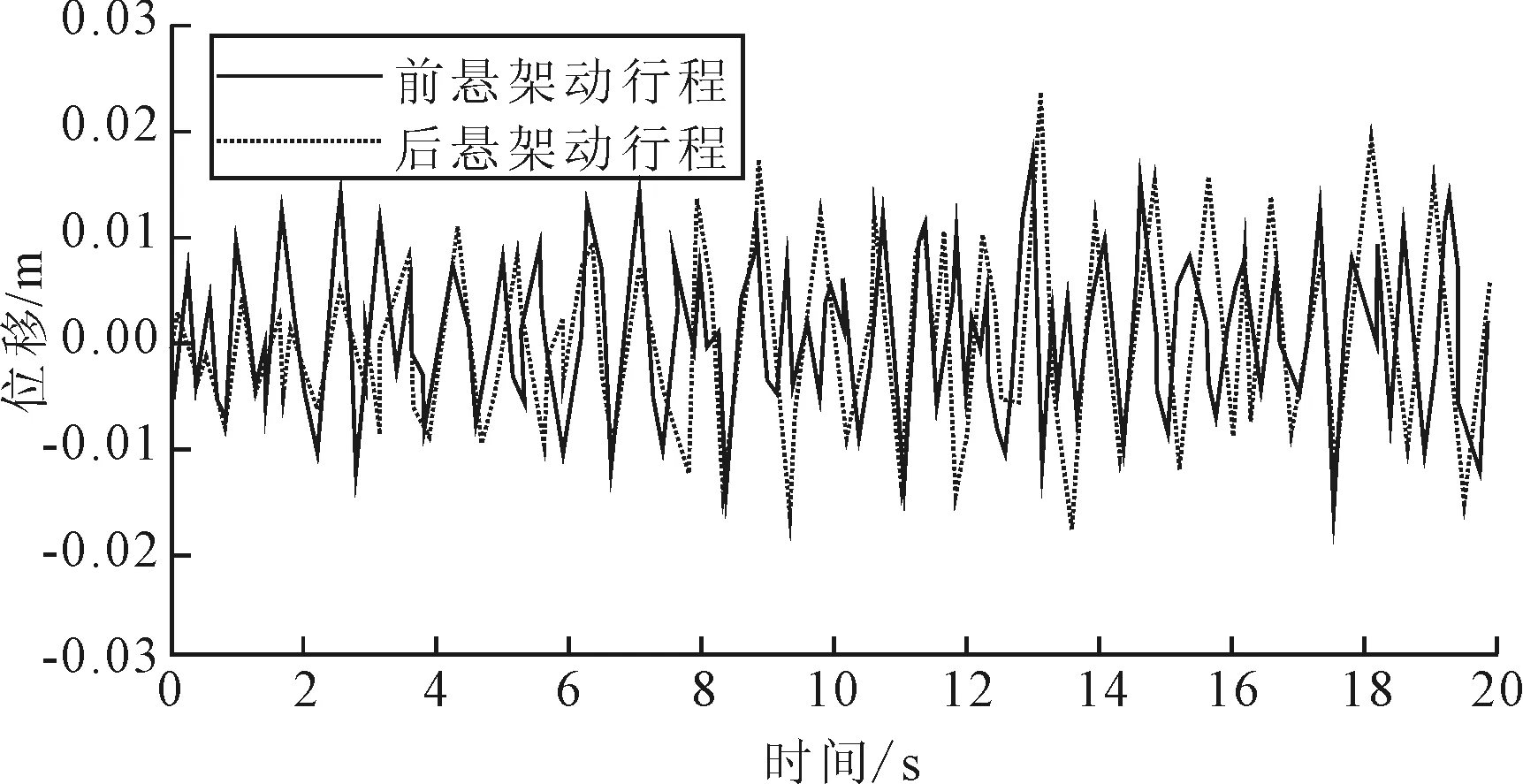
图5 60 km/h在B级路面上的悬架动行程曲线
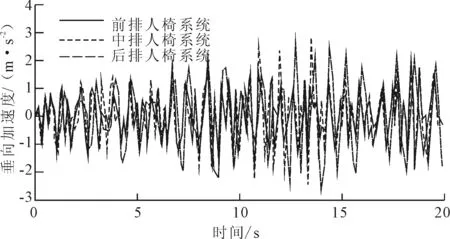
图6 60 km/h在B级路面上人椅系统加速度曲线
为更清晰地对比前、中、后三排人椅系统的垂向振动情况,求得各部分的垂向加速度均方根值如表1所示。

表1 三排人椅系统的加速度均方根值 m/s2
从图5~图6及表1可知,车辆正常行驶过程中,前、后悬架动行程相差较大,前中后三排人椅系统的振动情况有一定差别,并且后排的振动相较于前中排要明显剧烈些。说明研究跨界车悬架对乘员舒适性影响时,建立包含三排人椅系统的跨界车整车模型是有必要的。
3.2 线性与非线性仿真结果对比
整车模型以50 km/h,60 km/h,70 km/h,80 km/h,90 km/h的车速在B级路面直线行驶,分别进行十二自由度非线性模型和传统线性模型的仿真,仿真结果如图7~图8所示。
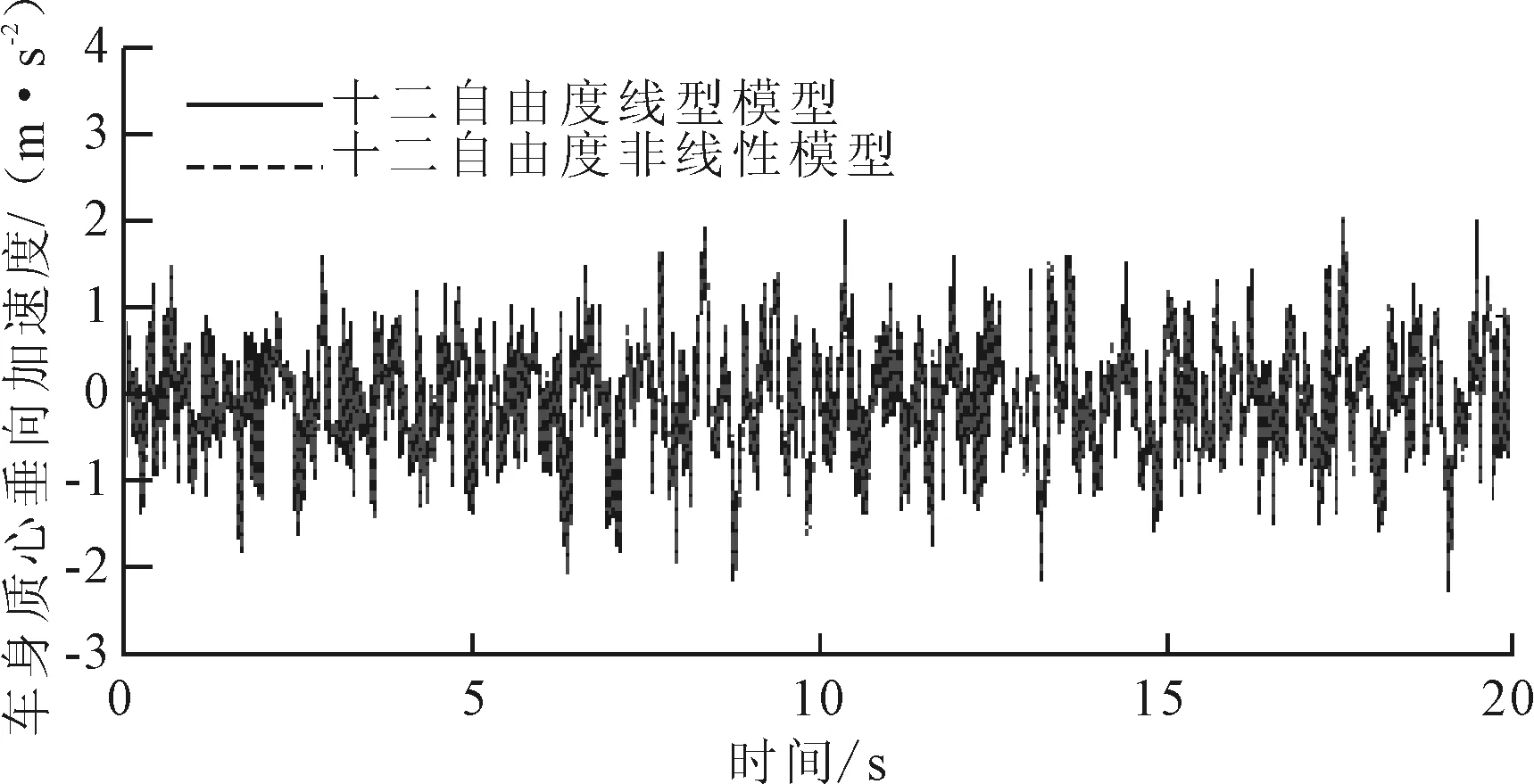
图7 60 km/h在B级路面上的车身质心加速度曲线

图8 不同车速下线性与非线性仿真结果
从仿真计算结果可以看出,两种模型车身质心的振动增长趋势是一致的,但在数值上有一定区别。说明在建立整车模型时考虑非线性因素的影响,模型仿真结果能够更接近真实的车辆系统,从而提高仿真分级的准确度。
3.3 非线性减振器对汽车平顺性的作用
跨界车以60 km/h的速度在B级、C级路面直线行驶及以80 km/h的速度在C级路面行驶时,分别进行十二自由度非线性模型和传统线性模型的仿真计算,各评价指标的均方根计算结果如表2~表4所示。
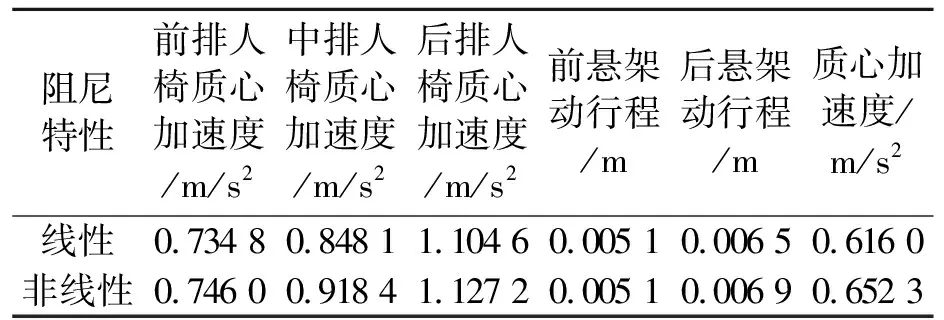
表2 跨界车以60 km/h行驶在B级路面下阻尼线非线性特性影响
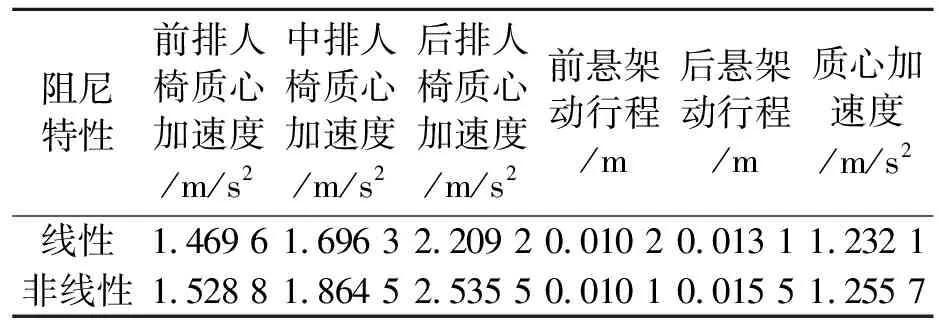
表3 跨界车以60 km/h行驶在C级路面下阻尼线非线性特性影响
将表2~表4中结果进行对比分析,得出以下结论:
(1)阻尼非线性模型的引入对后悬架动行程的影响最大,其次是人椅系统,而前悬架动行程几乎不受影响。
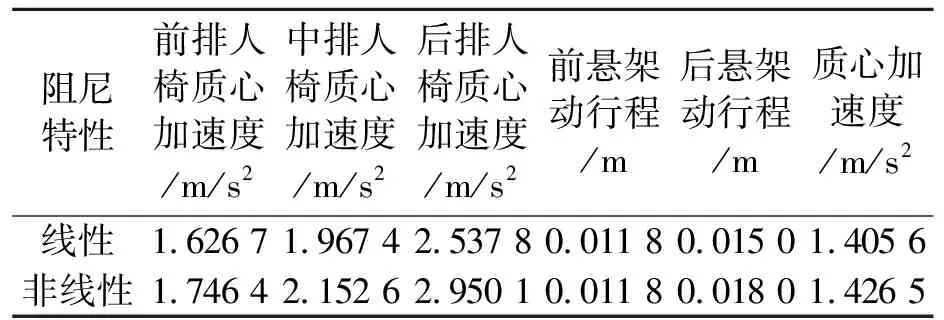
表4 跨界车以80 km/h行驶在C级路面下阻尼线非线性特性影响
(2)车速一定时,路面等级越低,车身振动越大。同样的,路面不平度系数一样时,车速增加也会恶化汽车的行驶平顺性。
(3)随着行驶条件变差(路面等级变低或车速增加),阻尼非线性对人椅系统及后悬架动行程的影响增大,但对质心加速度的影响趋势变小。
以上分析结果表明:悬架阻尼非线性特性对整车性能有一定影响,且影响程度随路面等级、速度改变而变化,可见不可忽视阻尼的非线性特性对跨界车性能的影响。
4 结论
(1)以实验数据为依据建立了分段线性的减振器阻尼非线性模型,将建好的模型嵌入到传统线性模型中,得到跨界车的十二自由度非线性模型。路面输入考虑了左右轮相干性和前后轮迟滞性的影响,与以往的线性模型相比,仿真能够更真实地反映车辆行驶过程中车身质心加速度等的变化情况。
(2)通过典型工况仿真结果可知,前、中、后三排人椅系统质心垂向振动加速度有一定差别,因此在研究跨界车乘坐舒适性时三排人椅系统应该被考虑在内。
(3)通过不同工况下的仿真结果对比分析可知,随着车速及路面等级的变化,人椅系统、悬架动行程及车身质心加速度都有一定程度的变化,且非线性与线性模型的仿真计算结果也有差别,可见在研究车辆性能时,建立可靠的非线性模型是至关重要的。
