水力喷射径向水平井钻井水力参数计算及优选方法
2018-10-15李根生黄中伟高辉窦亮彬
毕 刚,李根生,屈 展,黄中伟,高辉,窦亮彬,赵 凯
(1.西安石油大学 石油工程学院,陕西 西安 710065;2.陕西省油气井及储层渗流与岩石力学重点实验室,陕西 西安 710065;3.中国石油大学(北京) 油气资源与探测国家重点实验室,北京 102249)
引 言
水力喷射径向水平井技术完全依靠水力能量破岩的射流钻头与高压软管的配合在地层中钻进[1]。由于高压软管尺寸有限,其通过的钻井液流量较小,钻井液压力经连续油管及高压软管的沿程损耗后,真正分配给射流钻头的能量极其有限。为了寻求合理的水力参数配合,使井底获得最优的水力能量分配,从而达到最优的井底优化效果,需要在了解射流钻头水力特性、循环能量损耗规律、径向水平井岩屑运移规律和地面设备特性的基础上,对径向水平井水力参数进行优化设计[2]。国外学者对径向水平井水力参数的研究主要集中在循环压耗方面,从二十世纪末至今,Mishra and Gupta[3],Mashelkar and Devarajan[4],Shah[5-6]为代表对于非牛顿流体在连续油管中的流动特性进行了理论和实验研究。国内研究起步较晚,并且基本都停留在理论和数值模拟研究,牛涛[7]等人对于微小井眼的系统压耗进行了研究。张晋凯[8]等人提出了一个新的连续油管螺旋段的磨阻系数公式并进行了数模验证。马东军[9]等人提出了连续油管侧钻径向水平井循环系统压耗计算模型。目前,关于水力喷射径向水平井完整的水力参数计算及优化方法研究较少。
1 径向水平井水力参数计算方法
1.1 钻进最小排量
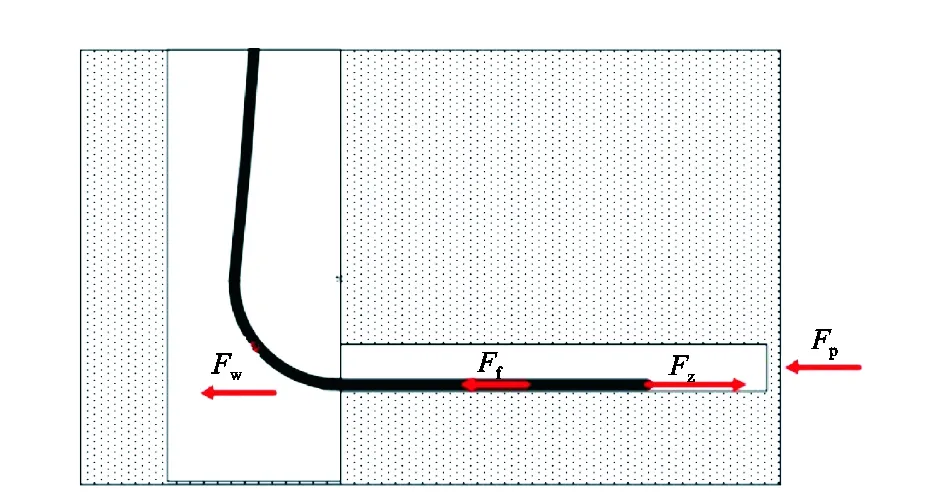
图1 高压软管钻进受力分析Fig.1 Mechanical analysis of high pressure hose in drilling process
根据现场实际工况,径向水平井在钻进过程的受力如图1所示,主要包括:水射流钻头提供的自进力Fz(动力),高压软管在水平段与井壁的摩擦阻力Ff,以及高压软管过转向器时受到的摩擦阻力Fw,射流钻头前端所受外部流体的压力Fp。设高压软管在水平延伸方向所受到的合力为F,则
F=Fz-Ff-Fw-Fp。
(1)
(1)自进力计算模型
根据笔者之前研究成果[10]可知,射流钻头的自进力Fz的计算式为
(2)
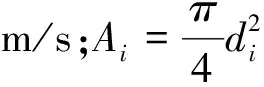
射流钻头的各喷嘴流速与各自的局部阻力系数相关,建立各喷嘴的伯努利方程:
(3)
式中:Zin为射流钻头入口处比位能,m;Zout为孔眼出口处比位能,m;ζi为第i(i=1,2,3,…,m)个正向孔眼的局部阻力系数,无因次;ζj为第j(j=1,2,3,…,n)个正向孔眼的局部阻力系数,无因次。
由式(3)得方程组
(4)
其中:
(5)
式中,n为射流钻头前向喷嘴个数,di为前向喷嘴直径,m为射流钻头后向喷嘴个数,dj为后向喷嘴直径。
将式(4)和(5)代入式(2)可得到射流钻头自进力关于钻头结构参数和水力参数(排量Q)的计算模型,根据现场施工参数可求得自进力。
(2)水平井壁对高压软管系统的阻力计算模型
在径向井钻进过程中,高压软管水平段受到重力、浮力和滑动摩擦阻力作用,可得滑动摩擦阻力
Ff=μqhKBL,
(6)
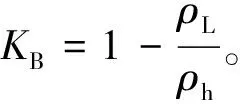
(7)
式中:L为目前所钻径向分支长度,m;qh为高压软管线重,kg/m;KB为浮力系数;ρL为钻井液密度,kg/m3;ρh为高压软管密度,kg/m3。
(3)转向器对高压软管系统的阻力计算模型
为了分析转向器轨道与高压软管之间的受力情况,对高压软管在转向器内运动过程中所受摩擦力进行实验测试。具体过程为:将转向器固定在实验台架上,高压软管一端封闭,并连接拉力计,另一端连接试压泵,通过试压泵向高压软管内打入静压液体,测量匀速水平拉动高压软管的拉力,通过实测可以得到高压软管在不同内压下通过转向器的滑动摩擦阻力Fw,在该实验条件下两者之间的关系如图2所示。通过线性拟合,得到摩擦力与高压软管内压力之间的关系式为:
Fw=aphd+b。
(8)
式中:a和b为方程拟合系数,单位分别为N/MPa、N,phd为转向器处高压软管内流体的压力,MPa。

图2 高压软管过转向器滑动摩擦阻力与内压关系Fig.2 Relation between sliding frictional resistance of high pressure hose passing through deflector and internal pressure
(4)射流钻头前端所受外部流体的压力
在实际工况下,转向器内被水充分润滑,而高压软管的内压为高压软管段的压耗,由于在软管不同位置软管所受内压值不同,取以软管半长处的压力作为软管内压的平均值,然后由软管承压值推算滑动摩擦阻力值。
射流钻头前端所受外部流体的压力Fp可由式
(9)
计算。式中,D为射流钻头外径,mm。
根据上述分析,求得射流钻头自进力及各阻力以后,即可求得高压软管和射流钻头水平钻进的合力F。显然,当F>0的时候,径向水平井才能水平钻进不断延伸井眼长度,即:
F=Fz-Ff-Fw-Fp>0
(10)
将射流钻头自进力及各阻力的计算模型代入式(10),设定相关参数,即可得到径向井延伸最小排量。
1.2 携岩最小排量
径向水平井的携岩过程与传统水平井钻井有着很大不同。径向水平井钻进过程中产生的岩屑沿着水平井眼运移出水平段,最后进入垂直井筒中预留的沉砂口袋,并不排出井筒。同时,在整个钻进过程中其钻杆是不旋转的。
径向水平井的携岩与连续油管钻水平井携岩过程很相似,H.Cho[11]对连续油管钻水平井的岩屑传输过程进行了详细的分析,可以大体分为3个过程:当排量足够大时所有的岩屑以悬浮状态运移;随着排量的降低,岩屑为3层流动,最上层为悬浮运移层,中间层为一层翻滚运动的岩屑床,最底层是固定岩屑床,整体看来就是一个个连续的岩屑床整体向前运移;当排量足够低,3层流动转变为2层流动,上层基本为单相流体流动,下层为固定不动的岩屑床。根据以上水平井岩屑运移规律,可以定义2个环空临界速度,第一临界流速(Critical resuspension velocity,CRV)和第二临界流速(Critical deposition velocity,CDV),CRV是指固定不动岩屑床开始运动的环空临界流速,CDV是指悬浮岩屑刚开始形成岩屑床的临界流速[12]。
径向水平井井筒的清洁程度直接决定了高压软管与井壁之间的摩擦力,对于其水平延伸能力有较大影响,第二临界流速要大于第一临界流速,因此取CDV为径向水平井环空携岩最低反速标准。
根据文献[13],Oroskar and Turian的CDV临界流速模型[14]比实测值通常要高5%~30%,其临界流速计算式为:
(11)
其中,ρm和μm为固液两相混合液的密度与黏度,混合液的密度与Thomas黏度计算式分别为:
ρm=Ccρs+(1-Cc)ρL;
(12)
(13)
因此径向水平井的携岩最小排量
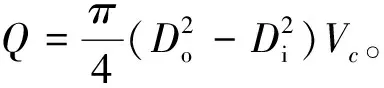
(14)
式中:Vc为临界流速,m/s;ρs为固相颗粒密度,kg/m3;ρL为液相密度,kg/m3;ρm为混相液体密度,kg/m3;μm为混相液体黏度,Pa·s;μL为液相液体黏度,Pa·s;S为固液相密度比,ρs/ρL;Cc为固相体积浓度;d为颗粒直径,m;D为水平段环空水力直径,m;Do为井眼直径,m;Di为高压软管外径,m;χ为颗粒沉降阻力系数,估算值为0.95。
1.3 钻进最大排量
地面泵的工作参数对径向水平井高效开采和安全钻进有重要影响,施工排量过高容易造成循环系统的压耗过大,使泵压升高,管内流体的压力升高可能影响管线的安全工作。由于泵和管线需要在安全条件下连续工作,排量和泵压应在额定的范围内,因此需要对某一排量下的泵压进行估算,一方面合理选择排量使泵和管线在小于额定压力的条件下工作,另一方面最大限度地发挥泵的工作性能,增大径向水平井的延伸极限,从而提高采收率。因此,径向水平井钻进过程中需要满足条件:
(15)
式中:pr,p为泵的额定泵压,Pa;pm,ct和pm,fh分别为连续油管和高压软管的最大工作压力,Pa;Q和Qr分别为泵的工作排量和额定排量,m3/s。
泵的额定功率、额定泵压和额定排量的关系为:
Prη=prQr。
(16)
式中:Pr为泵的额定功率,W;η为泵的效率,无因次。
因此,径向水平井钻进最大排量可由式(15)和式(16)确定。
1.4 循环系统压耗计算
水力喷射径向水平井钻井过程中,水功率从泵沿着连续油管、高压软管传递到射流喷嘴,然后经水平段环空返回至主井筒中,不考虑地面管线的压耗,泵压等于流体在循环系统各部分中流动的压耗之和,即
pp=Δpct1+Δpct2+Δpfh+Δpjn+Δpha。
(17)
式中:Δpct1为连续油管螺旋段压耗,Pa;Δpct2为连续油管直管段压耗,Pa;Δpfh为高压软管段压耗,Δpjn为射流喷嘴压降,Pa;Δpha为水平段环空压耗,Pa。
马东军等人的研究[9]表明,水平段环空流体的流速较低,压耗较小,可以忽略不计。因此,可将式(17)简化得泵压的计算式
pp=Δpct1+Δpct2+Δpfh+Δpjn。
(18)
(1)连续油管螺旋段压耗
连续油管螺旋段的压耗计算式[9]为
(19)
式中:Lct1为连续油管螺旋段的长度,m;dcti为连续油管内径,m;D为连续油管滚筒直径,m。
为准确计算连续油管螺旋段压耗,对连续油管螺旋段压耗进行现场测试。在泵的排量为60 L/min时测得外径为0.025 4 m,内径0.021 m,滚筒直径1.375 m的4 km连续油管在螺旋状态下的压耗为22 MPa,本文根据实验结果对螺旋段压耗式(19)进行修正,修正后的连续油管螺旋段压耗计算式为
(20)
(2)连续油管直管段压耗
引入前人的研究结果,连续油管直管段的压耗计算式为[9]:
(21)
(3)高压软管段压耗
水力喷射径向水平井中,高压软管结构为内层是橡胶芯管,外层由钢丝缠绕结构组成。因为连续油管内管材料为金属,而高压软管内层材料为橡胶,所以关于高压软管的摩阻系数需在金属内平管摩阻系数的基础上进行修正。本文应用金属内平管摩阻系数公式计算高压软管压耗,并通过实验方法测量高压软管压耗,发现在相同管长、泵排量下,高压软管的实测压耗大约为计算值的2倍,修正后的高压软管摩阻系数的计算式为:
(22)
式中,ffh为高压软管摩阻系数,dfhi为高压软管内径。
求得摩阻系数后,根据范宁—达西方程,流体在管内的压耗可由式
(23)
求出。
把式(22)代入式(23)即可推导出循环系统中高压软管段压耗的计算式
(24)
式中,Lfh为高压软管段长度,m。
为了验证高压软管段压耗计算的准确性,对高压软管段压耗进行多次实验测试,测试方法为:选取长度为10 m和20 m的高压软管,将高压软管一端接柱塞泵出口并装有压力表,另一端放置于大气中,开泵后压力表所显示数值,就是这一段高压软管的压耗。对不同排量情况下的压耗进行测试,得出泵排量与单位长度高压软管压耗的关系曲线(图3)。可以看出,随着排量的增大,单位长度高压软管的压耗近似线性增加,因此实际试验时设定的排量不宜过大。并且相同流量下的20 m和10 m软管的压耗之差有逐渐增大的趋势,这也反映出在径向井钻井中,随着软管长度的增加,地面泵压上升得很明显。同时应用式(24)分别对长度为10 m和20 m的高压软管的压耗进行计算,所得结果如图3所示,由图可知,计算所得高压软管压耗随排量变化关系与实验测试值类似,且大小差别不大,相同条件下,实测值与计算值最大差值仅为实测值的5.08%。
由于不同的高压软管材料会存在差别,因此在制定施工方案前,可以利用上述测试和分析方法对不同规格和性能的高压软管内压耗计算公式进行修正。
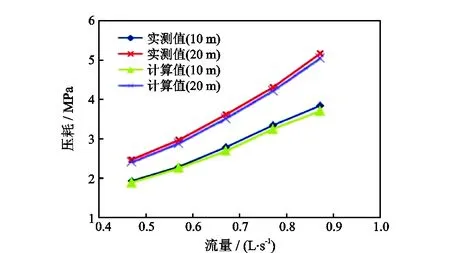
图3 高压软管压耗实测值与修正计算值对比Fig.3 Comparison between measured value and corrected calculated value of pressure loss of high pressure hose
(4)射流喷嘴压降
根据李根生等人的实验结果[15],射流喷嘴压降可通过式
(25)
计算。式中,C为喷嘴流量系数,无因次。
2 水力参数优化设计方法
径向水平井钻井水力参数优化方法是以最大射流冲击力为目标,考虑径向水平井的延伸能力、携岩能力和设备管线安全的基础上,对施工排量进行优化,从而得到最优排量,然后根据上述水力参数计算理论,优化确定其他水力参数。具体过程为:首先计算径向水平井钻进最小排量Qp和携岩最小排量Qr,取两者较大值作为最小排量Q0;然后逐渐增加排量,并计算对应的径向水平井钻井泵压Δp和射流冲击力Fj;以最大射流冲击力为目标,由径向水平井钻井泵压Δp可以推算出各设备管路工作压力pw,并根据现场工况,确定各管路、设备的安全工作压力psafe,在满足工作压力低于设备管路安全压力的基础上,得到最大射流冲击力的排量为最优排量。笔者应用VB软件编制了水力参数优化设计程序,计算流程如图4所示。
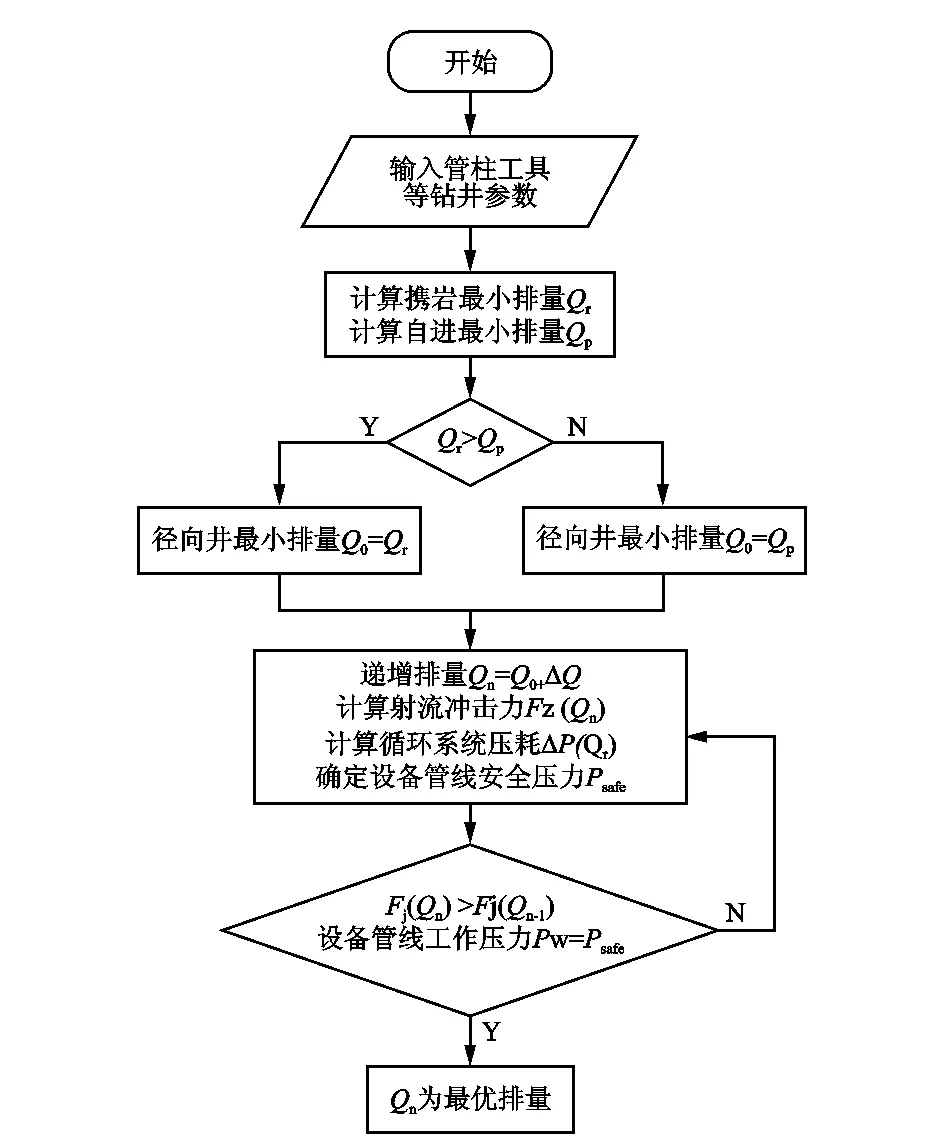
图4 径向水平井水力参数优化程序框图Fig.4 Flow chart of hydraulic parameter optimization of radial horizontal well drilling
3 实例计算
假设施工井深2 km,油层套管外径0.139 m,内径0.121 m,作业油管外径为0.073 m,现场使用的连续油管总长4 km(施工时,连续油管螺旋段2 km,直管段2 km),连续油管滚筒直径1.828 m,连续油管外径0.038 m,内径0.031 m,工作压力70 MPa,连续油管管壁粗糙度10.16×10-8m;施工流体使用清水,水的密度1 000 kg/m3,水的黏度10.05×10-6Pa·s,高压软管总长度50 m,高压软管外径0.014 m,内径0.01 m,工作压力40 MPa,爆破压力100 MPa,线重0.2 kg/m,材料密度2 183.6 kg/m3。
自进式射流钻头钻出的径向孔眼直径为0.04 m,井壁摩擦系数0.3,射流钻头内径为0.012 m,前向喷嘴6个,出射角度12°,直径0.7×10-3m,后向喷嘴9个,直径0.9×10-3m,出射角度30°,喷嘴流量系数0.8;根据钻井携岩常用参数,拟定岩屑颗粒直径0.004 m,颗粒密度2 650 kg/m3,岩屑体积浓度2%。
3.1 钻井最小排量
基于高压软管和射流钻头系统的动力方程,分别计算出径向水平井的自进力、转向器和水平井眼对高压软管的摩擦阻力,如图5所示,由图可知,随着排量的增加,自进力和转向器及水平井眼井壁对高压软管的摩擦总阻力都增大,当流量较小时,阻力增加速率更大,并且大于自进力,当流量增大到一定值时,自进力增加速率增大,此时,随着排量的增加,自进力的值都大于阻力值,选取此时的流量为径向水平井钻进最小流量,在该算例中,根据计算结果保持径向井自进的最小排量为42.25 L/min。基于径向水平携岩最小排量计算模型,在该算例中,可以计算出最小携岩排量53.91 L/min。
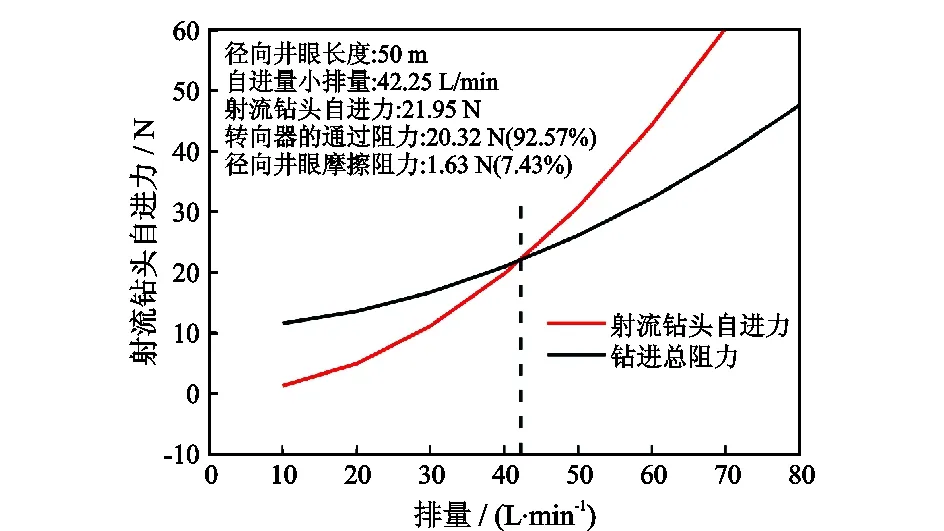
图5 径向井排量与钻进自进力及阻力关系Fig.5 Relationships between self-propelled force and resistance of jet bit and its flow rate
综上可得,保持水平井眼清洁和自进的径向井最小排量为53.91L/min。
3.2 径向水平井钻井最优排量
根据最大射流冲击力,确定径向水平井钻进的最优排量。由实际施工经验可知,在施工条件下排量越大射流冲击力越大,但是排量越大管线和地面设备所承受的压力也越大,根据径向水平井循环系统压耗各部分的计算公式,可算出各部分管线压耗和管线承压,如图6和图7所示,由于高压软管承受的压力由高压软管和水射流钻头的压耗决定,连续油管和柱塞泵承受的压力为循环系统压耗。其中,连续油管和柱塞泵的安全工作压力值为70 MPa,对应的安全排量为92.82 L/min;高压软管的安全工作压力值为60 MPa,对应的安全排量为89.81 L/min,该排量大于径向井最小排量,综上可得,为了保证安全钻进,选择89.81 L/min为该施工井的最优排量。

图6 径向水平井系统压耗与排量的关系Fig.6 Relationships between pressure loss and flow rate of radial horizontal well system
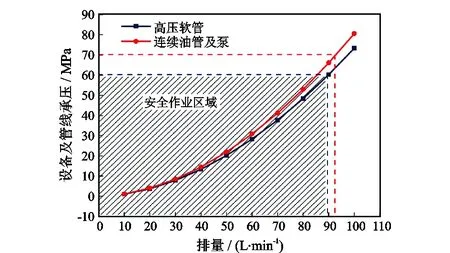
图7 设备及管线承压与排量的关系Fig.7 Relationships between pressure-bearing of equipment and flow rate
4 结 论
(1)连续油管侧钻径向水平井钻井与常规井眼钻井水力参数设计的不同主要表现在以下几方面:岩屑运移规律、循环系统压耗、钻头水射流特性以及地面设备特性等。
(2)给出了水力喷射径向水平井钻进最小排量及携岩最小排量的计算方法,提出了高压软管的压耗计算公式,并与实测高压软管压耗数据进行对比,相同条件下,实测值与计算值最大差值仅为实测值的5.08%,可以满足工程计算要求。
(3)以最大射流冲击力为目标,综合考虑钻进与携岩需要的最小排量和管线的承压能力,优化了径向水平井作业的最优排量,初步形成了径向水平井钻井水力参数优化设计方法。根据此方法,可得到径向水平井钻井过程中的最优排量,从而得到其他最优参数,可为水力喷射径向水平井技术现场配套设备和施工参数的选择提供依据。
