海上稠油聚合物驱剖面返转机理及影响因素

未志杰，康晓东，孙 哲，刘玉洋，张 健

(1.海洋石油高效开发国家重点实验室，北京100028； 2.中海油研究总院有限责任公司，北京 100028)

引 言

海上油田聚合物驱具有多层合注渗透率级差大、原油黏度大的特点，实施以来收到了明显的增油降水效果[1-2]，然而也出现了部分受效井含水回返、产聚浓度高且上升速度快等问题，聚合物利用率下降。研究发现，这与“剖面返转”有关，即在注聚过程中较低渗层相对吸液量先上升而后下降的现象。剖面返转发生后，聚合物纵向波及能力持续降低，层间矛盾更为突出，导致中后期聚合物在较高渗层低效循环，不利于低渗层剩余油的有效动用与聚合物驱油作用的充分发挥[3-6]。

目前聚合物驱剖面返转相关的研究，主要针对中等黏度稀油油藏晚期注聚的情形[3-4]，这与海上聚合物驱油田油稠、注聚时机早、合注渗透率级差大的特点有显著区别，且侧重剖面返转抑制/控制手段[5-7]，对剖面返转本身尤其是诱导其产生的力学机理的剖析有待深入。此外，目前研究手段一般采用室内物理模拟方法[4,5,7]，周期长，成本高，受人为因素影响大，缺乏数学模型进行快速定量表征，且所考察的影响因素相对受限。基于此，本文开展了海上多层稠油聚合物驱剖面返转机理及影响因素研究，通过构建非均质油藏聚合物驱吸液剖面数学模型，揭示剖面返转产生的力学机理，较全面分析剖面返转影响因素，获得影响剖面返转的关键因素及其变化规律，为聚合物驱持续高效开发提供指导。

1 非均质油藏吸液剖面数学模型

1.1 吸液剖面方程

对于多层非均质油藏而言，各层的注入体积流量可表示为

(1)

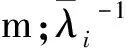
(2)

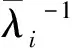
引入注入孔隙体积倍数Qi，定义为各层累积注入量与该层孔隙体积的比值(PV)，则各层注入速度也可以表示为注入孔隙体积倍数的函数，即

(3)

式中：VPV,i为第i层的孔隙体积，m3；L为注采端距离，m；φi为第i层孔隙度；t为油田开发时间，s。

联立式(1)与式(3)，可得

(4)

则层间视黏度关系满足

(5)

1.2 视黏度方程

(6)

1.2.1 水驱阶段 由Buckley-Leverett公式，水驱过程的连续性方程为

dxi=LQidf′w,i。

(7)

式中：fw,i为分流量，f′w,i表示fw,i关于含水饱和度Sw,i的偏导数，即f′w,i=∂fw,i/∂Sw,i。

给定相渗曲线与油水黏度，则油水总体相对流度λT,i是含水饱和度Sw,i的函数，即λT,i=λw,i+λo,i=g(Sw,i)；且在注入水波及区域内，分流量导数f′w,i是Sw,i单调函数，即f′w,i=h(Sw,i)，则Sw,i=h-1(f′w,i)。故总体相对流度可表示为f′w,i的函数，即

λT,i=g(Sw,i)=g(h-1(f′w,i))=m(f′w,i)。

(8)

若注入水已经在产出端突破，则将式(7)与式(8)代入式(6)得

df′w,i=n(Qi)。

(9)

若注入水尚未突破，则推进前缘位置xwf,i=LQif′wf,i，代入式(6)，得

(10)

1.2.2 聚合物驱阶段

聚合物为高分子化合物，在地层孔隙中存在不可波及区域，业界采用不可波及孔隙体积数IPV来表征。结合描述水驱过程的Buckley-Leverett公式，聚合物驱连续性方程为

(11)

聚合物具有增加水相黏度、降低水相有效渗透率的作用(吸附滞留导致)，则聚合物驱波及区总体相对流度与水波及区有所不同，即

(12)

相应地，第i层聚合物波及区分流率为

(13)

参考水驱阶段，推导出聚合物驱阶段的视黏度为前置水驱段累积注入量Qw,i、聚合物注入量·Qp,i的函数，即

(14)

其中聚合物推进前沿Lp,i=LQp,i/(1-IPVi)×f′pf,i。式中：f′pf,i表示聚合物推进前缘处分流率关于含聚水饱和度的偏导数。

1.2.3 后续水驱阶段

后续水驱阶段的视黏度为水驱段累积注入量Qw1,i、聚合物段累积注入量Qp,i、后续水驱注入量Qw2,i的函数，即

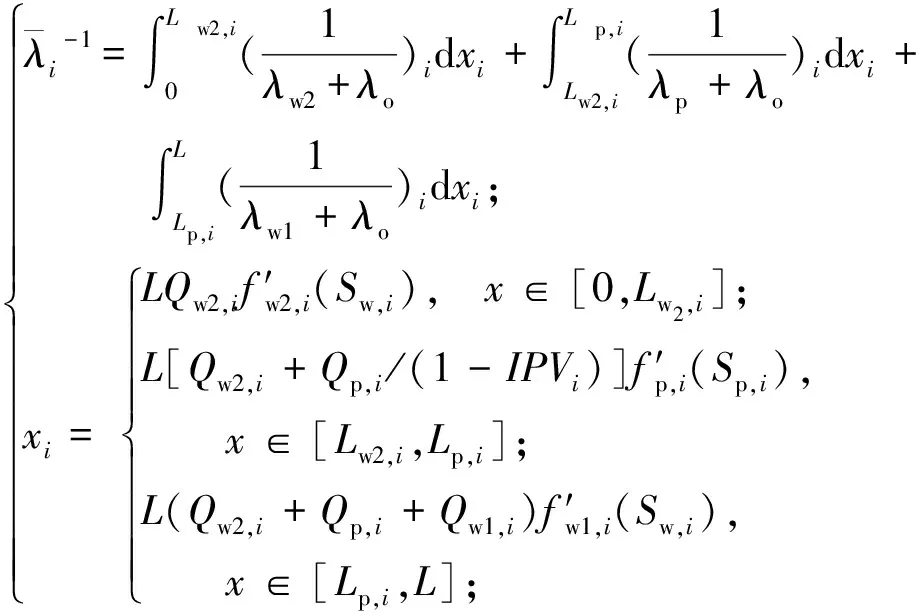
(15)

式中聚合物推进前沿位置Lp,i、后续水驱推进前沿位置Lw2,i为

(16)

(17)

1.2.4 约束方程

qdt=∑VPV,idQi。

(18)

对式(18)两边积分，可得

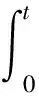
(19)

1.2.5 方程组求解

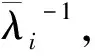
(20)

方程组(20)涉及复杂的非线性求解，直接计算困难且耗时费力，需要采用Newton-Raphson 迭代方法求解得出。应用Matlab软件编制了迭代求解程序，能够方便快捷地得到不同时刻各层累积注入孔隙体积数Qi，进而获得各层视黏度及各层相对吸液量，注采端压差可根据各层视黏度间接求得。

1.3 准确性验证

--模型准确性通过对室内实验结果的历史拟合来验证。双层并联长岩心驱替实验条件如下：①结合渤海SZ油田的油层物性参数，制作人造均质长方岩心，岩心规格4.5 cm×4.5 cm×30.0 cm，岩心饱和油范围60%～68%；②原油和航空煤油按一定比例配成模拟油，在60℃下黏度为70.0 mPa·s；③采用非稳态法测量了两块岩心的相对渗透率曲线，归一化后的相对渗透率曲线如图1所示(以束缚水饱和度下油相相对渗透率作为基准渗透率)；④模拟平台实际配制聚合物条件，采用地层水配制、污水稀释的方式配制1 750 mg/L聚合物溶液，目标黏度8.0 mPa·s；⑤水驱阶段注水速度2.0 mL/min，注水0.23 PV后转入聚合物驱，聚驱阶段注入速度1.0 mL/min，注入0.50 PV聚合物溶液时转入后续水驱，直至累计注入2.0 PV。驱替过程中，实时计量各层注入量、产液量以及注采端压差等数据。

图1 不同渗透率岩心的相对渗透率曲线Fig.1 Relative permeability curves of cores with different permeability

应用计算模型对岩心驱替结果进行了拟合，对比指标包括各层相对吸液量以及压力数据，模型计算结果与实验结果对比如图2所示，两者相对偏差低于5.0%，吻合度较好。

图2 实验结果与模型计算结果对比 Fig.2 Comparison of experiment data with calculation data of relative imbibition profile and injection-production pressure difference

2 剖面返转力学机理及影响因素分析

应用多层非均质油藏吸液剖面数学模型，对渤海稠油油田开展了聚合物驱剖面返转力学机理及影响因素研究。参考渤海SZ油田特征参数，建立了典型模型：①双层层状油藏，行列式井网，井距300 m，垂向有效厚度均为15 m，渗透率分别为500′10-3μm2、2 000′10-3μm2，渗透率级差为4；②压力、体积、温度等采用油田实际数据(地层原油黏度70.0 mPa·s)，两层的归一化相对渗透率曲线如图3所示，相比较低渗层，高渗层两相共渗区的范围更大，束缚水饱和度与残余油饱和度值更低，残余油饱和度下水相相对渗透率更高，等渗点对应含水饱和度更低；③注入聚合物质量浓度为1 750 mg/L，对应地下工作黏度8.0 mPa·s，残余阻力系数为1.6；④注入速度0.06 PV/a，注采比1.0；⑤注入顺序，先水驱1.0 PV，之后注入0.67 PV聚合物，最后转入后续水驱。

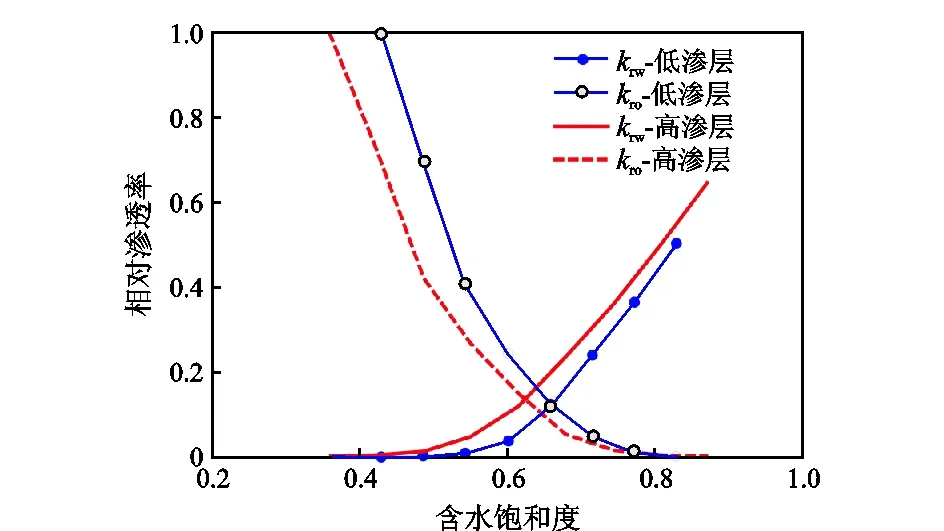
图3 目标油田不同渗透层相对渗透率曲线Fig.3 Relative permeability curves of different permeabilitylayers in the target reservoir

2.1 剖面返转力学机理

稠油聚合物驱剖面变化如图4所示：水驱阶段，较低渗层相对吸液量持续下降；注聚后，先近乎线性快速上升，达到峰值后折返并直线下降，吸液量高峰值甚至高于初期值，剖面整体形态呈现倒“V”型。

图4 吸液剖面随注入孔隙体积倍数的变化情况Fig.4 Variation of imbibition profile with injection volume

下面分析聚合物驱剖面返转产生的力学机理，聚合物驱过程中低渗层相对吸液量及其导数为

(21)

(22)

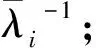
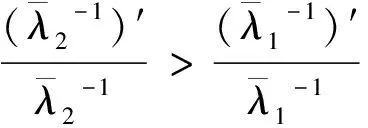
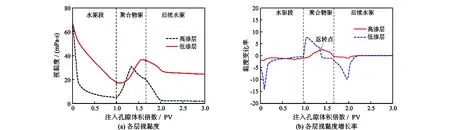
图5 各层视黏度及其增长率随注入孔隙体积倍数的变化情况Fig.5 Relationships between apparent viscosity and its varying rate of each layer and injection volume

2.2 影响剖面返转的敏感因素分析

由多层油藏吸液剖面数学模型，影响稠油聚驱吸液剖面的因素包括原油黏度、渗透率级差、高低渗层孔隙度比、低高渗层厚度比以及聚合物浓度。

为定量刻画剖面返转现象，引入返转幅度和返转时机两个参数，定义返转幅度Δη为低渗层相对吸液高峰值与转注聚时相对吸液量之间的差值(见图4)，返转时机Δt为低渗层相对吸液量达到高峰时所对应的累积注聚孔隙体积倍数。

2.2.1 原油黏度 图6为不同原油黏度下各层相对吸液量变化情况。当原油黏度在5～70 mPa·s变化时，随着原油黏度升高，剖面形态由倒U型转变为倒V型，低渗层同期相对吸液量及高峰值降低，剖面返转时机提前，低渗层吸液量明显降低。可见聚合物驱改善纵向波及的能力随着原油黏度增大而降低，稠油油藏吸液剖面趋于倒V型，易造成聚合物在高渗层低效循环，不利于低渗层剩余油动用及聚合物高效利用。

图6 不同原油黏度时吸液剖面变化情况Fig.6 Variation of relative imbibition profiles of different permea-bility layers with injection volume under different oil viscosity

2.2.2 渗透率级差 图7为不同渗透率级差下相对吸液量变化情况。当渗透率级差在4～10变化时，随着渗透率级差增大，低渗层相对吸液量与返转幅度均显著下降，返转时机显著提前。聚合物驱改善纵向波及的能力随着渗透率级差增大而明显下降，低渗层总吸液量降低。

2.2.3 高渗层与低渗层孔隙度比 保持高渗层孔隙度0.32不变，依次改变低渗层孔隙度至0.08、0.16、0.24、0.32，相应的高低渗孔隙度比分别为4.0、3.0、2.0、1.0，各孔隙度比下相对吸液量变化情况见图8。随着低渗层孔隙度降低， 该层相对吸液能力升高，峰值吸液量提高，返转时机推迟。值得注意的是，当孔隙度低至0.08时，吸液剖面在注水和注聚过程中均保持不变，剖面返转现象消失，分析认为此时高低渗层K1/φ1=K2/φ2，根据方程式(5)，两层渗流阻力时刻相同，各层前缘推进速度相同。因此，渗透率级差一定时，低渗层孔隙度越小，越有利于实现各层均衡推进，返转幅度越低，返转时机推迟。

图7 不同渗透率级差时吸液剖面变化情况Fig.7 Variation of relative imbibition profiles of different permeability layers with injection volume under different permeability difference

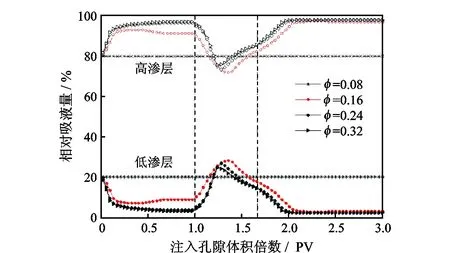
图8 不同孔隙度比时吸液剖面变化情况Fig.8 Variation of relative imbibition profiles of different permeability layers with injection volume under different porosity ratio

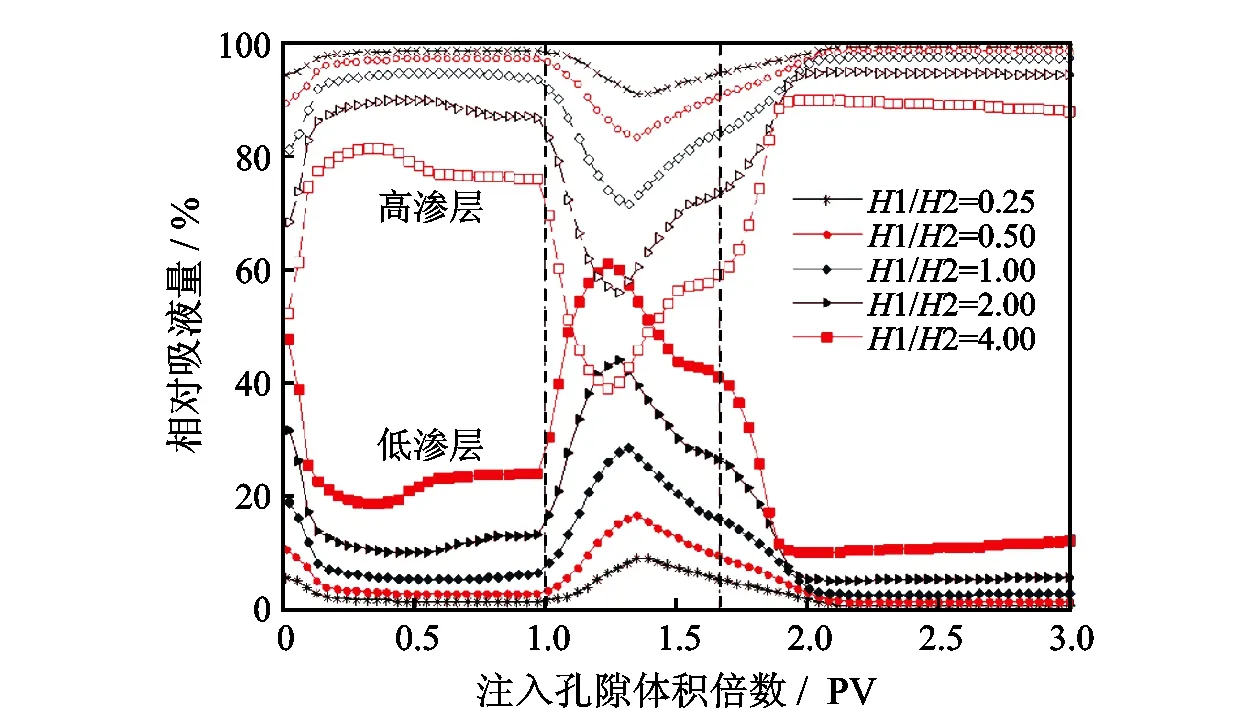
图9 不同低高渗层厚度比时吸液剖面变化情况Fig.9 Variation of relative imbibition profiles of different permeability layers with injection volume under different layer thickness ratio

2.2.4 低高渗层厚度比 图9为不同低渗层与高渗层厚度比下各层相对吸液量变化情况。当厚度比在0.25～4.00变化时， 随着低渗层相对厚度增大，地层系数差异缩小，低渗层相对吸液量明显提高，高峰值及返转幅度均显著升高，返转时机提前。当厚度比为4时低渗层相对吸液量峰值为60.1%，大于同期高渗层的39.9%。

2.2.5 聚合物浓度 图10为不同聚合物浓度下相对吸液量变化曲线，当聚合物浓度在800～2 300 mg/L变化时，随着注聚浓度/黏度升高，低渗层相对吸液高峰值明显提高，但是返转时机显著提前，由0.49 PV提前至0.26 PV，低渗层剖面形态由倒V型向倒U型转变。聚合物调节剖面的能力随浓度的增大而升高，适当提高聚合物浓度，可有效提高聚合物纵向波及，提高低渗层剩余油动用程度。

图10 不同聚合物浓度时吸液剖面变化情况Fig.10 Variation of relative imbibition profiles of different permeability layers with injection volume under different polymer concentration

3 结 论

(1)基于多相渗流Buckley-Leverett方程的非均质油藏聚合物驱吸液剖面数学模型，可以实现对聚合物驱剖面返转的快速定量表征。

(2)聚合物驱剖面返转产生的力学机理是：聚合物优先注入高渗层，导致高渗层渗流阻力快速上升而低渗层变化相对迟缓，低渗层相对吸液量先提高，进而造成低渗层阻力增长率提升而高渗层减缓，两者相等时产生剖面返转，之后低渗层阻力变化率超越高渗层，致其相对吸液量回落。

(3)海上聚合物驱油田多层合采渗透率级差大、原油黏度高、注聚时机早的特点，使剖面返转形态倾向于呈现倒“V”型，易造成聚合物在高渗层低效循环。

(4)随着原油黏度或渗透率级差的增大、低渗层相对厚度或聚合物浓度的降低，低渗层剖面返转高峰值与返转幅度降低，返转时机提前，低渗层吸液量降低，聚合物改善纵向波及的能力降低。随着低渗层孔隙度下降，返转时机推迟，该层相对吸液量升高，当孔隙度比值接近渗透率级差时，剖面返转现象甚至可消失。