面向环境适应性的无人机飞行姿态模拟器设计与仿真

杨剑锋，黄创绵，李小兵，潘广泽，闫攀峰，袁 婷

(1.工业和信息化部电子第五研究所，广东 广州 510610;2.广东省无人机可靠性与安全性工程技术研究中心，广东 广州510610;3.广东省工业机器人可靠性工程实验室，广东 广州 510610;4.广东省电子信息产品可靠性技术重点实验室，广东 广州 510610;5.航空工业第一飞机设计研究院，陕西 西安 710000)

0 引 言

随着无人机技术的飞速发展及市场需求的日益增长，旋翼类无人机越来越多地被用于航拍、农林、安防、电力等行业[1]。由于消费级无人机技术门槛低，市场前景又巨大，缺乏统一制造要求，不仅一些从事航空相关配套的企业大力发展无人机，许多航模企业也可通过购买零件来完成无人机的组装。由于缺乏有效的测试方法与技术，无人机可靠性与安全性水平参差不齐，因此无人机安全事故频频发生。目前关于无人机可靠性与安全性的测试技术相关研究较少[2-3]，特别是关于无人机环境适应性的测试方法与技术研究则更少[4]，亟需相关的检测装置及测试方法来规范无人机市场的发展。

为了分析风场对无人机性能的影响，美国航空航天局（NASA）的Russell等[5]研发一种综合测试系统来测试无人机单个电机及整机在风场环境下的升力随转速及风速的变化情况。国防科技大学的谷新宇等[6]提出一种微小型电动无人机动力系统试验台。北京航空航天大学的Deng等[7]提出一种关于无人机飞行安全性控制与地面测试的思想，通过利用地面测试数据对无人机飞行安全进行评估与认证来提高无人机的飞行安全性。以上研究大都从无人机性能和安全性提升的角度开展的，而关于无人机环境适应性测试装置的研究则较少。对于消费级无人机，常见的环境适应性测试项目包括：温度、抗风等级、低气压等[8]，目前的测试手段由于受到技术条件及成本的限制，无人机只能固定与温度或低气压试验箱中进行测试，无法进行飞行状态的测试，或者固定于试验箱中进工作时温度及低气压适应性的测试，该试验方法无法真正得到无人机的飞行性能水平。

基于此，本文提出一种用于模拟无人机飞行姿态的模拟器。该模拟器可以通过输入飞行任务剖面实时模拟无人机的飞行姿态，并利用ADAMS和Matlab/Simulink对该姿态模拟器进行联合仿真分析[9]。

1 飞行姿态模拟器结构及使用场景

1.1 模拟器结构设计

对于飞行器来说，其空间飞行位置信息可以用横向（sway）、升沉（heave）、纵向（surge）来表示，姿态信息可以用俯仰（pitch）、偏航（yaw）、横摇（roll）来表示，见图1。由图可知，如果要模拟飞行器的飞行姿态，飞行模拟器的自由度至少为3个，但对于四旋翼无人机而言，由于其俯仰角与横摇角相同，而且对于飞行试验来说，影响较小，因此飞行器模拟器只需两个自由度即可满足四旋翼无人机的飞行姿态模拟要求。本文设计无人机飞行姿态模拟器的结构如图2，该模拟器主要包括偏航轴系统、俯仰轴系统和无人机负载平台，其中偏航轴系统由偏航轴伺服电机、偏航轴减速器、偏航轴制动器、偏航轴联轴器、圆锥滚子轴承等部件组成，俯仰轴系统由俯仰轴伺服电机、俯仰轴减速器、俯仰轴联轴器、滚珠轴承等部件组成。工作原理：当飞行姿态模拟器未通电时，俯仰轴与偏航轴上的制动因断电而自锁，当在上位机输入无人机的飞行姿态曲线时，伺服控制器控制俯仰轴与偏航轴上的伺服电机进行联动，同时带动各轴上的减速器进行旋转，从而驱动无人机负载平台进行俯仰与偏航角的转动，进而模拟无人机的实时飞行姿态。

图1 飞行器空间位姿信息表示方法

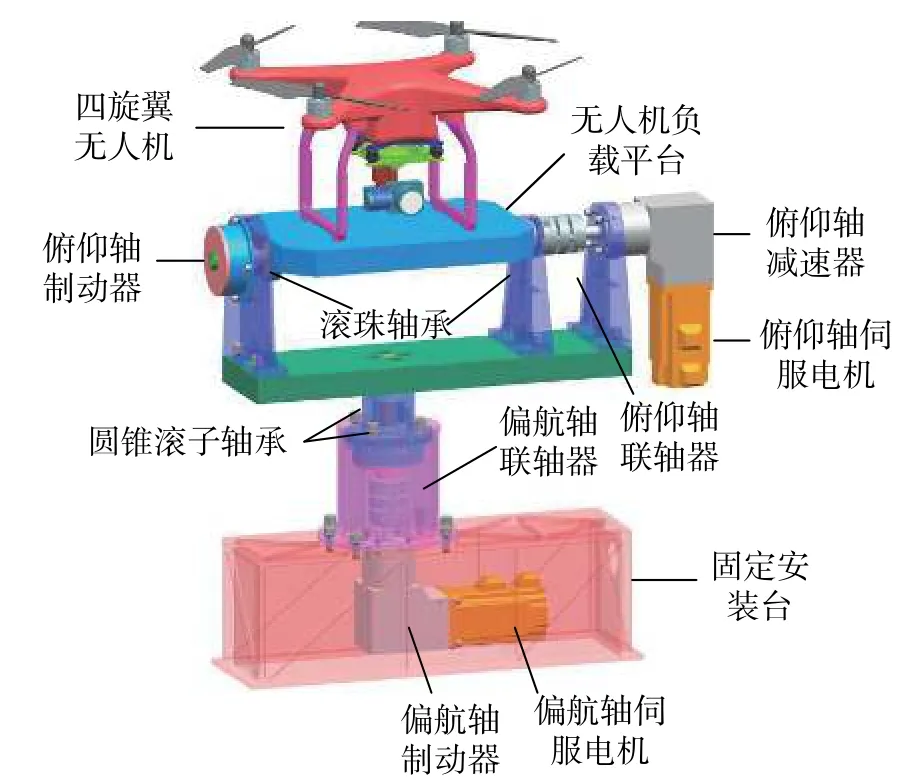
图2 无人机飞行姿态模拟器结构

1.2 飞行姿态模拟器使用场景

本文研制的无人机飞行模拟器的主要目的是模拟四旋翼无人机的飞行姿态，通过与其他环境试验设备协同配合，可以用来测试无人机飞行时的环境适应性。图3为无人机飞行姿态模拟器放置在温度-湿度-高度三综合试验箱中对无人机的温度、湿度、高海拔的环境适应性进行测试。该使用场景可以测试无人机在不同飞行姿态下对温度-湿度-高度综合应力环境的适应能力，其中温度-湿度-高度三综合试验箱由广州五所环境仪器有限公司生产，可满足GJB 150.2A——2009相关试验标准。同时本文研制的飞行姿态模拟器也可以放置在台风淋雨系统（该系统为本实验室开发研制）中对无人机的抗风及抗雨性能进行飞行测试，如图4所示。该使用场景可以测试无人机在不同飞行姿态下应对吹风与淋雨的适应能力，其中台风淋雨系统由课题组开发，最大风速可达 28.5 ～ 32.6 m/s，可满足 GJB 150.8A——2009淋雨试验的相关标准。

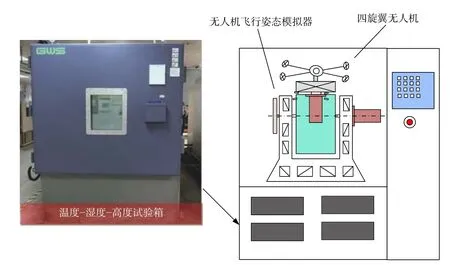
图3 无人机飞行姿态模拟器置于三综合试验箱

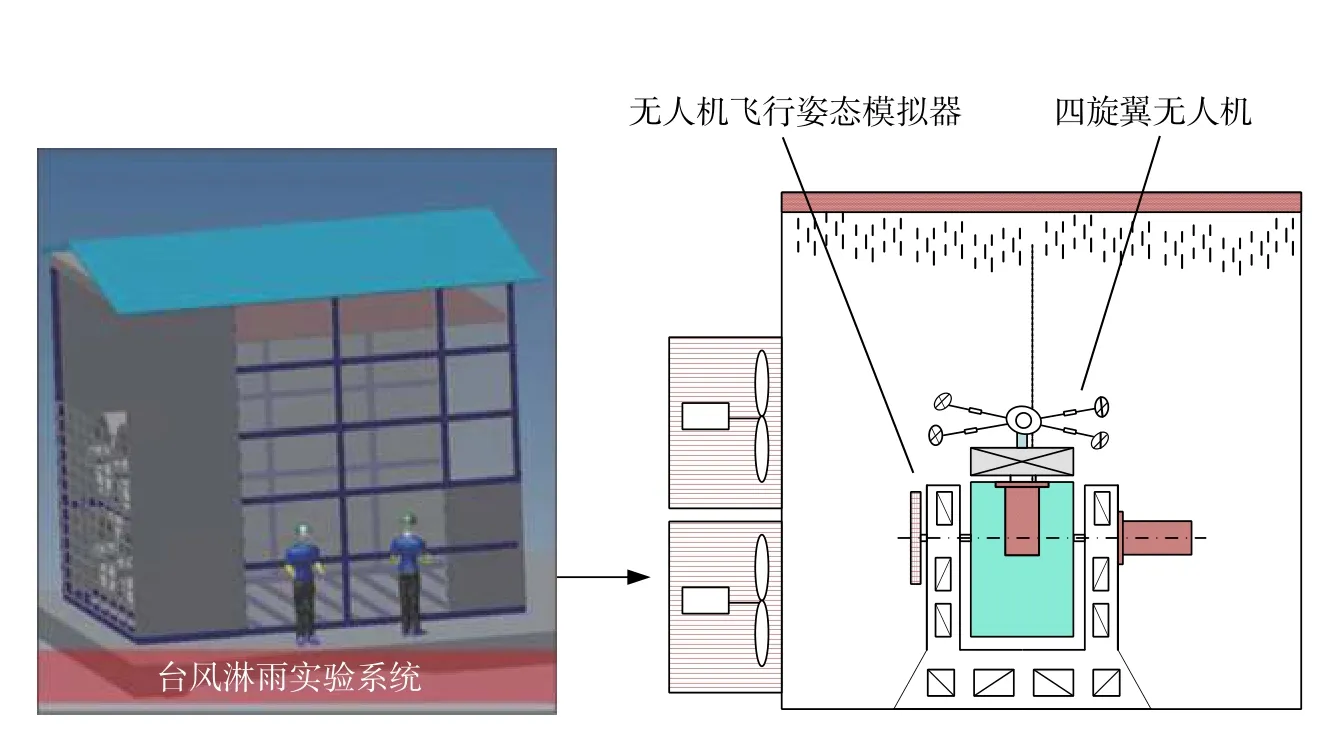
图4 无人机飞行姿态模拟器置于台风淋雨系统

2 联合仿真技术方案

本文利用ADAMS与Matlab/Simulink[10-11]进行联合仿真分析，利用Simulink进行控制系统的设计，来控制ADAMS[12]中的虚拟样机模型，并对仿真结果进行分析，从而优化设计。图5为联合仿真的技术方案框架图，首先通过CAD软件建立机械系统的数字样机模型；接着利用多体系统仿真软件建立机械系统的虚拟样机，在虚拟样机里定义好监控参数及接口变量，并生成Matlab/Simulink能识别的状态空间方程；然后在Matlab/Simulink建立机械系统的控制系统模型，设置好仿真参数，并在Matlab的工作空间中定义好ADAMS生成的状态空间方程的环境变量；最后进行仿真分析，该仿真方法可以实现Matlab/Simulink与ADAMS生成的状态空间方程之间数据的双向传递，仿真的核心思想为利用Matlab/Simulink进行控制系统的仿真，ADAMS进行虚拟机械系统的仿真，相互之间的桥梁为状态空间方程，以此达到仿真结果与实际结果一致性最大化的目标。

3 伺服控制系统工作原理

无人机飞行姿态模拟器的偏航轴与俯仰轴的控制原理相同，其控制框图见图6所示。将转轴的转动角速度设置为伺服系统的控制目标变量，比较偏航轴的实际速度与目标速度之间的误差；根据控制系统电压-扭矩的传递函数计算得到伺服电机的输出扭矩，通过伺服电机对偏航轴的工作速度进行调整，并将速度信息反馈给伺服控制系统，进行反馈，形成闭环控制。

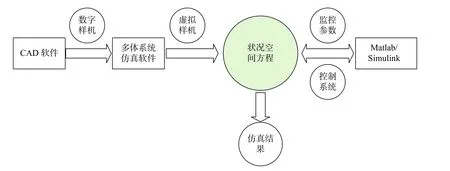
图5 联合仿真技术方案框架图

图6 伺服控制系统框图

根据直流伺服电机的工作原理，可得电机的电压-角位移传递函数，如图7所示。图中Va、Ia、Ra、La分别为伺服电机控制回路的工作电压、电流、电阻和电感；Cm和Ce分别为伺服电机转矩系统和电动势系数；J为电机轴总转动惯量；Md为电机轴输出扭矩；Mf为电机轴摩擦扭矩；ω和θ分别伺服电机轴角速度和角位移。

图7 俯仰轴伺服电机控制策略框图

对于图7的控制策略有两种仿真建模方法，方法1为伺服电机的电压-扭矩传递函数在Matlab/Simulink中建立，输出扭矩-角位移传递函数在ADAMS中建立。方法2为从伺服电机的输入电压到俯仰轴转动角位移之间的传递函数建模全部在Matlab/Simulink中完成。方法1与方法2相比，其好处是可以充分考虑伺服电机的转动惯量及摩擦扭矩对控制系统的影响。

方法1中伺服电机电压-扭矩的传递函数可以表示为

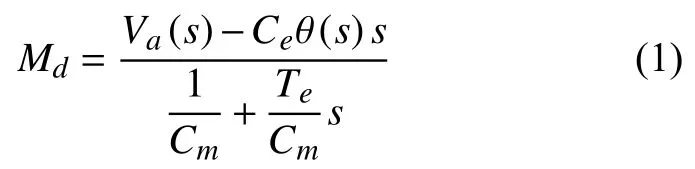
方法2中伺服电机电压-角位移传递传输可以表示为

其中Te和Tm分别为伺服电机控制回路电磁时间常数和电机常数，Te=La/Ra，Tm=RJa/CeCm。本文机-电系统联合仿真伺服控制系统的实现采用方法1，根据式(1)在Matlab/Simulink中建立伺服电机的控制系统。

4 ADAMS与Simulink联合仿真

4.1 联合仿真模型构建

在ADAMS/View中建立飞行姿态模拟器的虚拟样机模型，为简化仿真模型，删除所有连接件，并对材料参数相同的零部件进行了布尔合并处理，具体模型见图8所示。为实现与Matlab/Simulink之间数据的双向传输，在ADAMS模型中定义输入和输出变量，输入状态变量为偏航轴力矩（.MODEL_1.Yaw_torque）和俯仰轴力矩（.MODEL_1.Pitch_torque）；输出状态变量为偏航轴角位移（.MODEL_1.Yaw_Angle）、偏航轴角速度（.MODEL_1.Yaw_Angle Velovity）、俯仰轴角位移（.MODEL_1.Pitch_ Angle）、俯仰轴角速度（.MODEL_1.Pitch_ AngleVelovity）。利用ADAMS/Controls模块将建立的虚拟样机模型转成状态空间方程，并采用Simulink建立飞行姿态模拟器建立偏航轴和俯仰轴的PID伺服控制模型。在Matlab环境下建立联合仿真控制系统模型，该仿真模型包括俯仰轴伺服控制单元、偏航轴伺服控制单元、状态空间方程接口模块等3部分内容，如图9所示。偏航轴与俯仰轴的伺服控制系统相同，已俯仰轴为分析对象介绍了控制系统的基本特性，表1给出了俯仰轴伺服系统的基本工作参数。

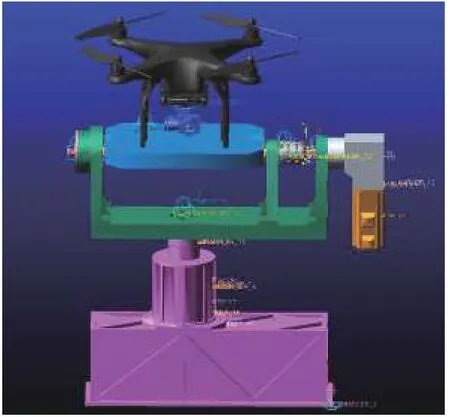
图8 无人机飞行姿态模拟器虚拟样机

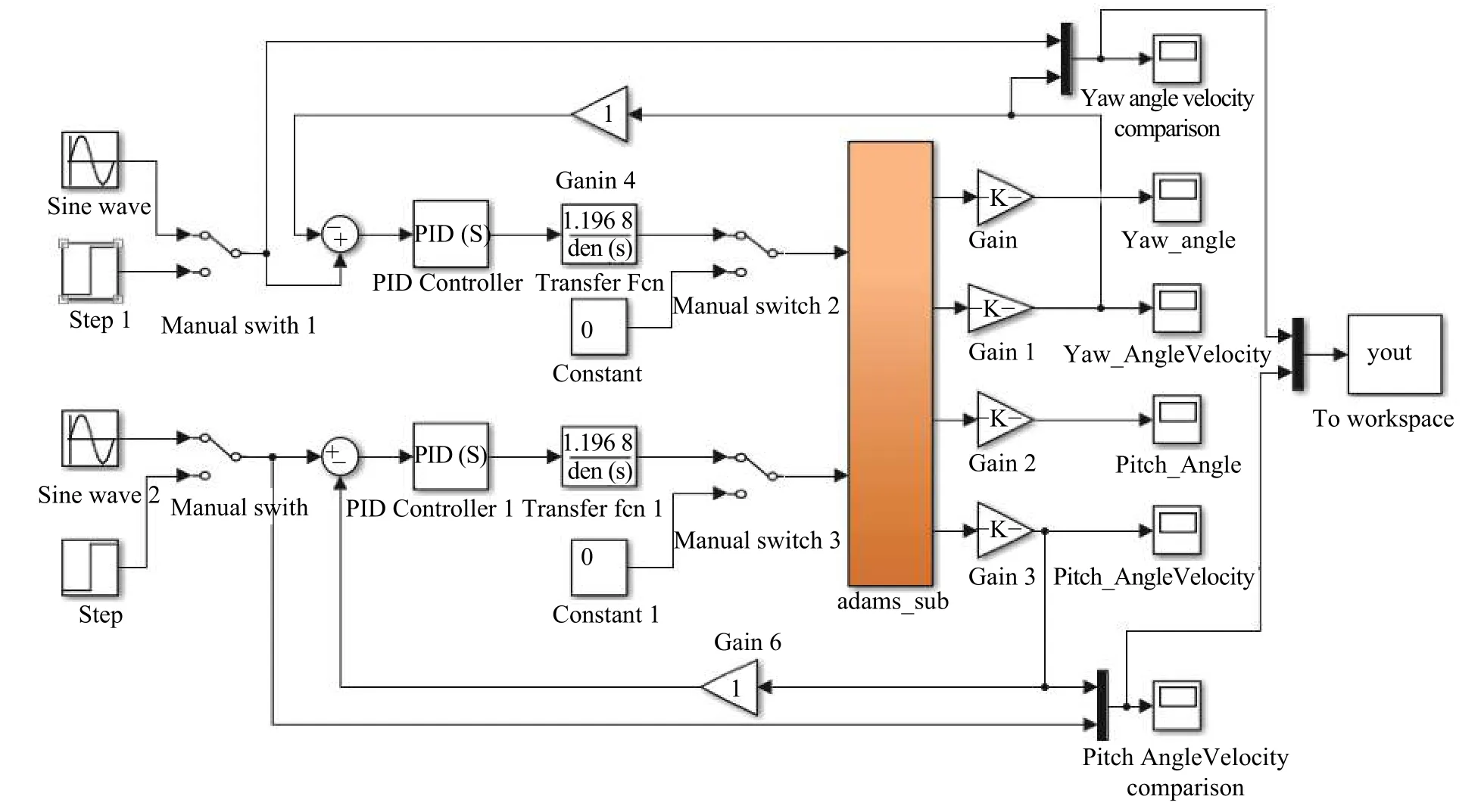
图9 无人机飞行姿态模拟器控制系统模型

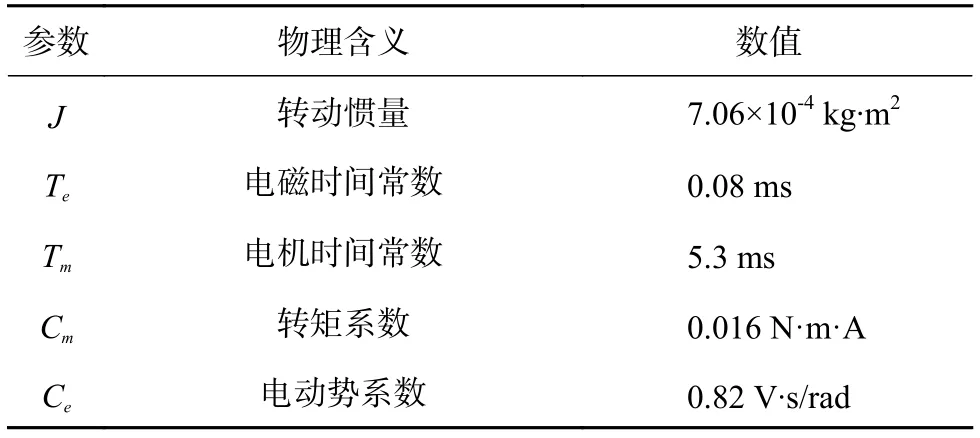
表1 俯仰轴伺服控制系统基本参数

4.2 联合仿真分析

在Matlab/Simulink求解器中设置数值分析方法为 ode3（Bogack–Shampine），采用固定步长，采样时间为0.001 s，动画模式为交互式，仿真模式为离散式。采用方法1进行伺服控制，分别设置目标信号为阶跃信号和正弦信号，得到偏航轴和俯仰轴的角速度响应及误差曲线，见图10和图11所示。由图10(a)可知，当目标函数为阶跃函数时，偏航轴伺服控制系统的超调量为8.25%，调整时间约为0.7 s，调整误差小于2%。由图11(a)可知，俯仰轴伺服控制系统的超调量为4.49%，调整时间为0.75 s，调整误差小于2%。设置偏航轴与俯仰轴的目标角速度都为 10 sin(0.4π·t)（°/s），可以得到偏航轴与俯仰轴的仿真曲线，见图10(b)和图11(b)所示。由图可知，在跟踪目标正弦信号的开始阶段，由于系统跟踪存在调整时间，跟踪曲线存在一定的延时，但考虑本机械系统为飞行姿态模拟器，只须复现目标曲线即可，延时对于测试结果影响较小，因此本文设计的PID伺服控制系统具有较好的波形复现性能。

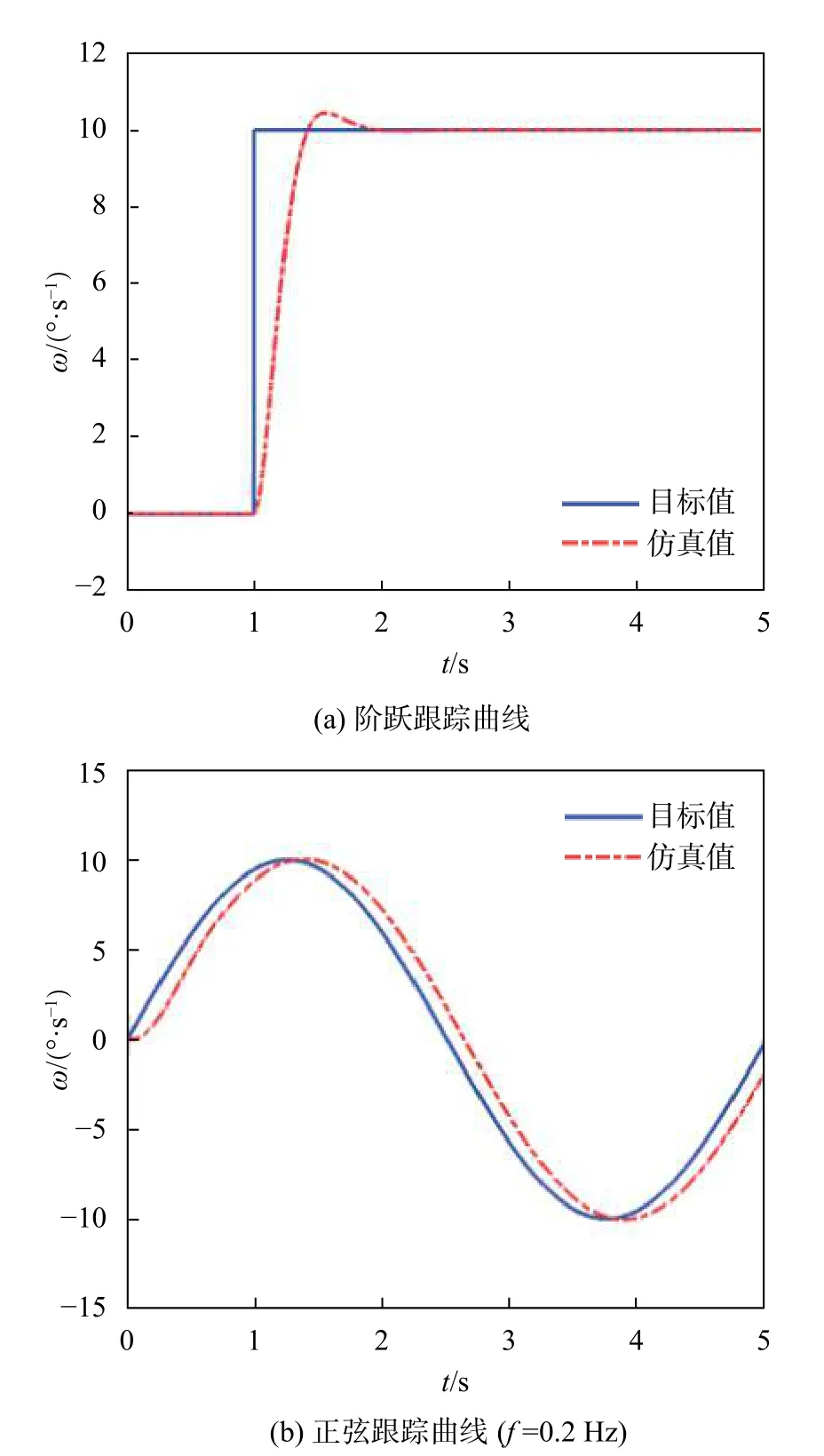
图10 偏航轴仿真曲线

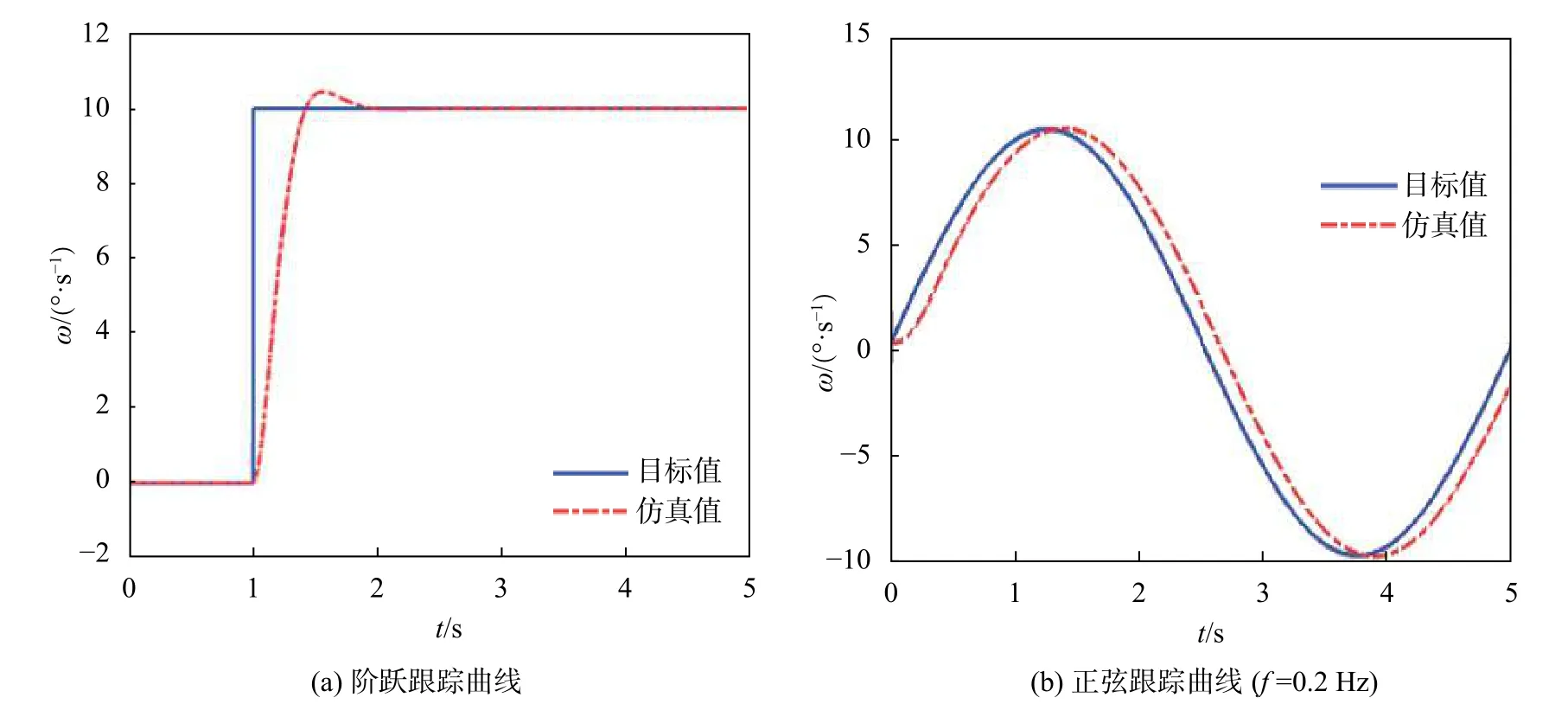
图11 俯仰轴仿真曲线

5 结束语

本文提出一种面向环境适应性的无人机飞行姿态模拟器，对该模拟器的伺服控制系统的工作原理进行了详细阐述。文中提出两种仿真方法，比较了其优缺点，并利用ADAMS与Matlab/Simulink对设计的飞行姿态模拟器进行了联合仿真，仿真结果表明：本文设计的飞行姿态模拟器整体机械结构及伺服控制系统对目标角速度曲线具有较高的复现能力，能较好地模拟旋翼类无人机的飞行姿态。同时，本文提出的联合仿真方法可为复杂机-电系统的设计与开发提供可靠依据，具有实际的工程价值和现实意义。