重力坝在两种溃决方式下的数值模拟研究

2018-10-15胡文兵伍学文胡海松

三峡大学学报(自然科学版) 2018年5期

柳滔胡文兵伍学文胡海松张杨

(1. 三峡大学水利与环境学院，湖北宜昌 443002； 2. 湖北能源集团溇水水电有限公司，武汉 430077)

1 研究背景

重力坝结构作用明确，设计方法简便，对地形、地质条件适应性强，主要依靠自身重量维持稳定，属于较安全坝型．尽管发生的重力坝溃决事故较少，但由于勘察、施工、设计和管理缺陷，重力坝溃决事故仍偶有发生．不同于土石坝的溃决有一个相对漫长的过程，重力坝的溃决大都在瞬间发生，故一旦溃决将给下游带来巨大的危害．

研究大坝的溃决方式一直是一项重要工作，这项工作的开展将有助于我们更加深入的了解大坝的溃决机理，也能对大坝溃决产生的危害有一个预估．吴世伟等[1]将重力坝的上下游水位、坝体坝基强度等作为随机变量，首次用随机有限元法探讨了重力坝在自重和水压等荷载作用下的最大可能破坏模式；傅忠友等[2]基于典型溃坝案例和重力坝工作机理，总结了重力坝溃决原因，并分析与讨论了溃决模式和溃决路径；胡江等[3]在极限倾覆失效状态研究的基础上，建立了包含主要极限稳定失效状态的重力坝的通用系统失效模型；姚霄雯等[4]根据收集的国内外74座混凝土坝溃坝资料，提出了混凝土坝的主要溃坝模式及其潜在的溃坝路径．

本文在总结前人研究成果的基础上提出假设，设计了两种重力坝溃决方式：1)滑移溃决，即坝基失稳导致坝体在水压的作用下整体向下游河道产生滑动而后冲走．2)翻倒溃决，即坝肩破坏导致坝体整体以坝基所在轴线为旋转轴向下游翻倒，而后以翻倒形态留在原地．如图1所示，这两种溃决方式分别对应坝基占主因和坝肩占主因导致的溃坝，通过研究它们的差异可以为重力坝设计施工及安全管理运行提供一定参考．

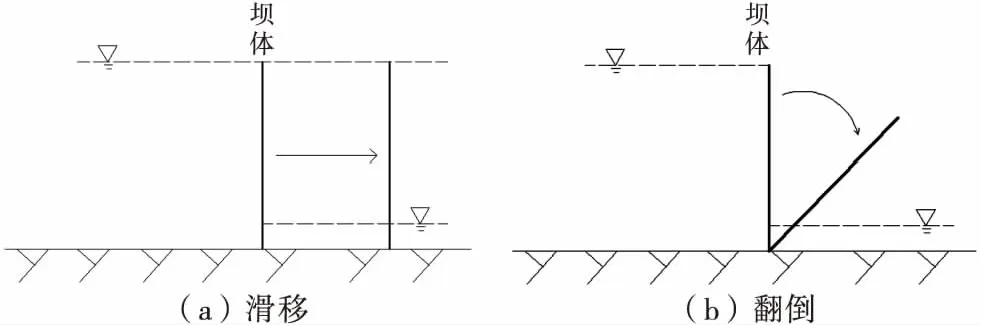
图1 两种重力坝溃决方式

2 数学模型

对溃坝水流的研究方法有物理试验和数值模拟两种．其中物理试验存在可重复性差、耗时耗力等问题，而数学模型经过精确的验证后能满足研究的需要，并且还能克服试验条件的限制，模拟更加复杂工况下的水流情况．众多学者[5-7]通过数值模拟的研究方法均得到了较好的结果．本文基于专业流体计算软件Flow-3D，采用RNGk-ε[8]模型，并结合VOF[9]法来模拟重力坝在两种溃决方式下溃口的水力学特性．

2.1 控制方程

连续方程：

动量方程：

紊动能k方程：

紊动能耗散率ε方程：

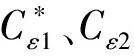
2.2 模型建立

数学模型是按某实际水库制作的物理模型以1∶1的比例建立．模型坝型选取混凝土重力坝，坝高50 cm，坝顶宽15 cm，坝底宽30 cm，斜坡比1∶0.7．溃决时坝前水面宽为100 m，溃决坝段为矩形，尺寸为30 cm×50 cm．数学模型整体构造如图2所示．

图2 模型整体构造

计算区域范围：x轴方向-227～608 cm，y轴方向-357～1 153 cm，z轴方向-53～53 cm．将计算区域范围划分为结构化网格，在坝体部分局部加密，总网格数为240万．

2.3 边界条件和初始条件

边界条件：整体计算区域上方采用大气压边界；出水口所在的面采用自由出流边界；除出水口外的其它3个侧面、底面均采用固体边界．

初始条件：在坝体以上河道设定水深为50 cm，坝体下游河道根据计算工况的不同设定水深为0 cm、10 cm、20 cm．设定河道的表面糙率为0.021 5．考虑到缩尺后溃坝时间的缩短，将时间步长设为0.01 s．

流量监测：Baffles在Flow-3D中定义为没有厚度的孔隙孔板，用来控制或引导水流．实际工作中，完全不影响水流运动，常用来测量通过某断面的水流流量与计算通过的颗粒数量．本文在溃口所在断面设置Baffles，以监测溃口流量变化过程．

2.4 模型验证

为验证所建数学模型的可靠性，将数学模型模拟的结果与物理模型试验中得到的同种工况下的溃口水位和流量数据验证．所选工况为上游水深50 cm，下游水深0 cm，溃决模式为漫顶溃决．验证结果如图3～4所示．

图3是在滑移溃决时溃口的水力参数变化情况，其中水位在下降约10 cm后达到最小值，而后渐趋稳定，试验值和模拟值基本一致；流量的变化中，模拟最大流量值比试验最大流量值大，相差4.49%，但它们的总体变化趋势基本吻合．

图4是在翻倒溃决时溃口的水力参数变化情况，其中水位的变化在0.3～1.2 s模拟值与试验值有一定偏差，且水位开始有一个急速下降的过程，这可能是因为翻倒后的坝体对水流有一定的阻碍作用，但它们的总体变化趋势比较吻合；流量的变化中，模拟值和试验值的最大值基本一致，而后的变化趋势也比较吻合．综上所述，所建数学模型准确可靠，满足继续研究的需要．

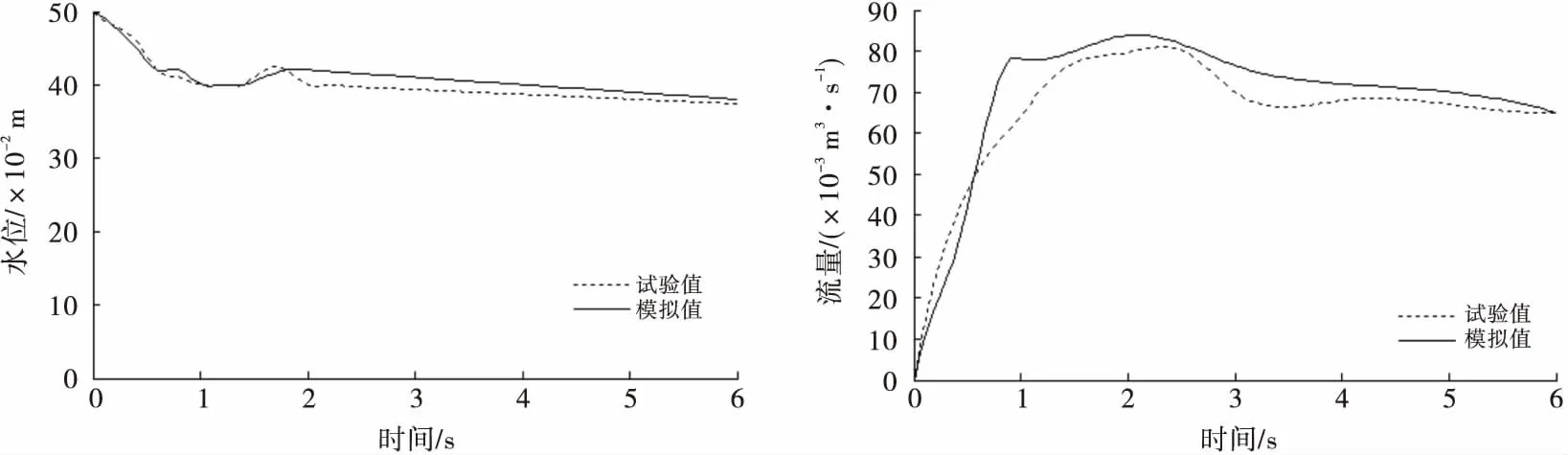
图3 滑移溃决时溃口水位、流量对比

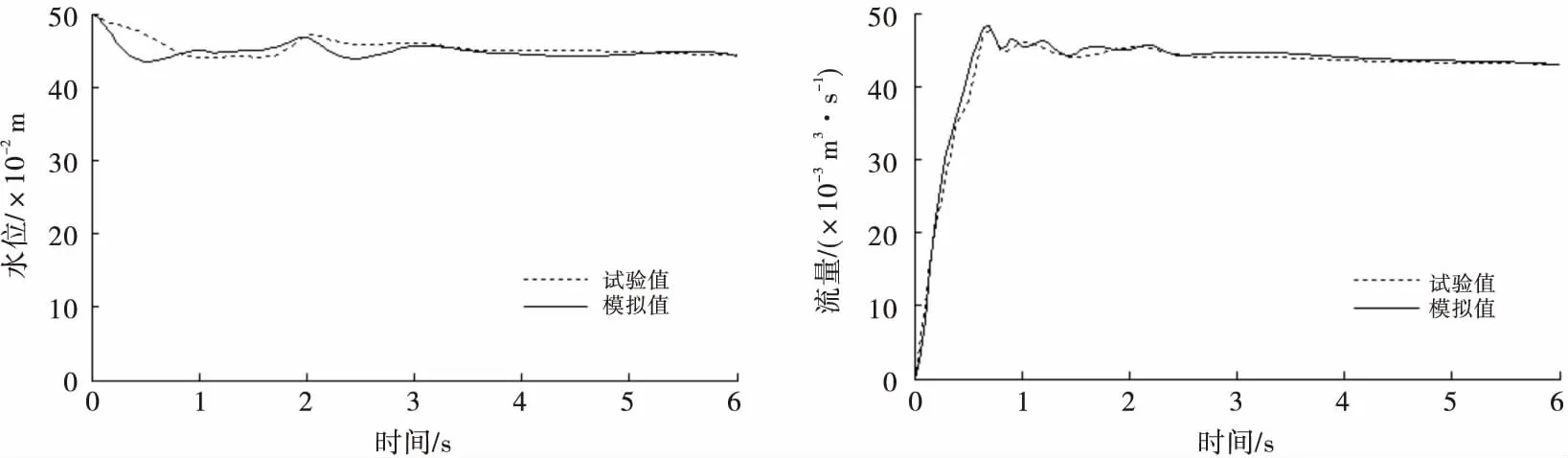
图4 翻倒溃决时溃口水位、流量对比

3 计算工况与结果分析

3.1 计算工况

在上述验证模拟的工况中，所选工况是下游无水的特殊情况，而一般大坝下游是存在一定水深的．所以，研究下游水深与大坝溃决时溃口最大流量的关系具有重要的实际意义，这不仅能得出危害最大的溃决方式，也能为水库的安全调度运行提供一定参考．根据溃决方式和下游水深可设计6种工况，见表1．

表1 设计工况

3.2 计算结果分析

从图5可知，工况1、工况2和工况3的溃口最大流量分别为45.31 L/s、68.14 L/s和83.89 L/s，最大相差46.26%，最小相差18.77%．流量都是先急剧上升而后缓慢下降，这是因为溃坝是在瞬间发生的，溃口从小到大的发展时间很短，当溃口稳定后水流出流受到限制，随着水库的蓄水流出，溃口流量逐渐下降；而下游水深对溃口水流有一定顶托作用，所以随着下游水深的增加，溃口最大流量也随之减小，并且流量的下降趋势变缓．

从图6可知，工况4、工况5和工况6的溃口最大流量分别为41.60 L/s、46.00 L/s和48.34 L/s，最大相差13.94%，最小相差4.84%．流量的变化也是先急速上升而后缓慢下降，原因也同滑移溃决时一样，但不同的是，由于翻倒溃决形成的溃口比滑移溃决小，且翻倒溃体留在原地形成阻碍，所以导致溃口最大流量也要小；同时下游水深的顶托作用依然存在，但由于溃口的缩小，所以相对滑移溃决，溃口流量的下降趋势更缓．

图6 翻倒溃决在不同水深下的溃口流量

对于在相同下游水深时，不同溃决方式也存在差异：对比工况3和工况6(下游水深为0 cm)，滑移溃决的最大流量比翻倒溃决大42.38%；对比工况2和工况5(下游水深10 cm)，滑移溃决的最大流量比翻倒溃决大32.49%；对比工况1和工况4(下游水深20 cm)，滑移溃决的最大流量比翻倒溃决大8.19%．这说明在下游水深的顶托作用下，溃决方式的差异变小了．