桥梁结构非平稳随机抗震分析

但庆文 张传勇 刘章军

(三峡大学 土木与建筑学院， 湖北 宜昌 443002)

桥梁结构是人类社会发展的重要基础设施，随着科技进步和建造材料的开发，桥梁结构日益朝着大跨高墩的方向发展，越来越多的大跨高墩刚构桥、斜拉桥以及悬索桥建成服役，这些桥梁结构在强震作用下都不可避免地会产生非线性响应．对大跨度桥梁随机地震响应分析和抗震可靠度评价是桥梁结构设计的重要内容，而地震动时程的模拟是基于动力时程分析的桥梁结构抗震研究所面临的首要课题[1]．由于强度非平稳地震动模型的物理意义明确、使用简便，人们大多采用其作为地震动输入模型[2-4]．然而，地震动的频率非平稳对结构的非线性动力作用同样重要，需要更全面真实地反映结构的动力响应，因此，近年来合理考虑地震动的全非平稳特性成为地震动建模的重点和热点．曾珂等人发展了一类地震动时变模型，该模型较好的考虑了频率非平稳性[5]；张翠然等人在Priestley[2]演变谱理论的基础上通过拟合目标演变谱构造了强度-频率非平稳地震动模型；同样地，胡灿阳等人在此演变谱理论基础上，通过引入了强度-频率双调制函数模型，建立了一类双调制地震动过程模型[6]；刘章军等人从工程应用的角度出发，通过构造与现行水工抗震规范相结合的强度-频率调制函数，建立了一类强度-频率演变功率谱模型[7]，其优点在于参数可以方便地由抗震规范确定，且适用于公路工程抗震规范．

本文将借鉴文献[7]中构造广义演变功率谱的思路，结合最新的《公路工程抗震规范》(JTG B02-2013)[8]，发展一类与最新桥梁抗震规范相结合的改进Kanai-Tajimi功率谱，同时考虑地震动的强度非平稳特性和频率非平稳特性，建立非平稳地震动过程的强度-频率演变功率谱模型．然后，结合强度-频率演变功率谱密度模型和非平稳地震动过程的谱表示-随机函数降维法[9-11]，生成610条与公路工程抗震规范相对应的地震波样本集合，并对模拟结果的二阶统计量、演变功率谱密度函数和平均反应谱进行了分析，以验证本文方法的有效性．最后，将生成的概率完备的代表性时程集合和概率密度演化方法[12-13]结合，对范和港大桥的随机地震动响应及抗震可靠度进行了精细化的分析．

1 非平稳过程模拟的谱表示-随机函数方法

根据非平稳地震动过程模拟的谱表示方法，对于零均值、双边演变功率谱密度函数为SX(t，ω)的非平稳地震动过程X(t)(一维单变量随机过程)可近似表示为[9]：

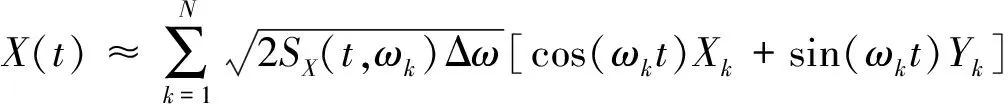
(1)

式中，SX(t，ω)满足SX(t，ω0)=SX(t，0)=0；Δω=ωu/N为频率步长，ωu为上截断频率，N为频率截断项数，ωk=kΔω．Xk和Yk(k=1，2，…，N)为一组标准正交的随机变量，其满足如下基本条件[9]：

E[Xk]=E[Yk]=0，E[XkYl]=0，

E[XkXl]=E[YkYl]=δkl

(2)

式中，E[·]为数学期望，δkl为Kronecker记号．

在式(1)中，当N取有限项时，X(t)的均方相对误差为[9]：

(3)

式中，T为地震加速度过程的持时．

在此模拟方法中，其核心在于确定式(1)中功率谱密度函数SX(t，ω)的表达式和正交随机变量{Xk，Yk}的表达式，利用随机函数的降维思想[11]，式(1)中的{Xk，Yk}可方便的确定为：

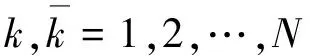
(4)

其中，基本随机变量Θ在区间(-π，π)上均匀分布．

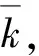
2 时-频非平稳地震动模型

在传统的结构非线性地震分析中，一般采用仅考虑强度非平稳的地震动模型，然而频率非平稳对结构的非线性分析同样有着重要的影响．为此，本文在平稳地震动过程的Kanai-Tajimi功率谱[14-15]基础上，采用文献[7]中的方法构造了一类时-频非平稳地震动模型．

首先，根据文献[14-15]，Kanai-Tajimi的广义功率谱可定义如下：

(5)

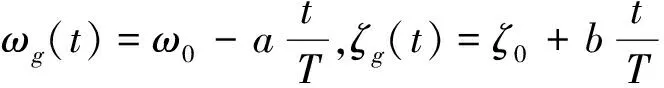
(6)

式中，ωg(t)和ω0分别为场地土的时变频率和卓越圆频率；ζg(t)和ζ0分别为场地土的时变阻尼比和阻尼比．参数ω0、ζ0和a、b可根据场地类别来确定；S0(t)为谱强度因子，其表达式为：

(7)

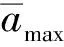
其次，选取强度调制函数，本文选取Shinozuka提出的一种强度调制函数[16]：

(8)

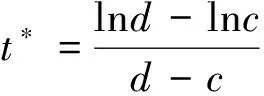
(9)

式中，t*为地震动峰值到达时间的均值，参数c和d可根据场地类别来确定，且参数c和d反映了地震动过程的强度非平稳性．

最后，根据上述Kanai-Tajimi的广义功率谱模型和强度调制函数，可以给出如下修正的演变功率谱模型：

SX(t，ω)=|f(t)|2S(t，ω)

(10)

式中，SX(t，ω)为演变功率谱密度函数．

图1为采用本文方法生成的时-频演变功率谱密度函数图，从图中可以看出在频域和时域内均表现出明显的非平稳特性．

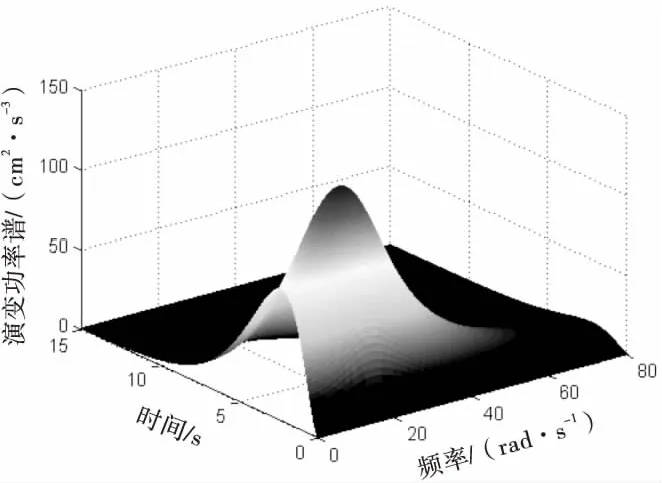
图1 时-频演变功率谱密度函数

3 非平稳地震动过程的模拟与验证

为了生成非平稳地震动代表性时程样本集合，首先需要对基本随机变量Θ选取代表性点集，本文对基本随机变量在区间(-π，π)上选取610个均匀散布的代表性点，同时计算每一个代表性点的赋得概率为1/610．然后，将选取的每一个代表性点代入式(4)中，并完成一一映射，便可得到标准正交随机变量{Xk，Yk}的代表性集合．最后，将正交随机变量{Xk，Yk}带入到非平稳地震动随机过程的谱表示-随机函数模拟公式(1)中便可生成非平稳地震动过程的代表性时程．

表1 演变功率谱模型参数

图2为采用本文方法生成的非平稳地震动过程代表性时程，从图中可知，代表性样本具备地震动时程的典型特征，且强震阶段一般出现在1/6～1/3持时范围内；图3为生成的610条加速度时程的平均傅里叶幅值谱，其反映了地震动能量在频域中的分布，从图中可以看出，不同频率谐波振动所携带的能量主要分布在0～15 Hz范围内．

图4为采用本文方法模拟的610条地震动加速度时程集合的均值及标准差与目标均值及标准差的比较图，从图中可知，模拟值与目标值十分接近，集合均值和集合标准差均在目标均值和目标标准差的上下波动，总体上与目标值的相对误差均在5%以内．对应地，图5为采用本文方法生成610条地震动加速度时程集合的估计反应谱与规范反应谱的比较，从图中可知，模拟值与三段式的规范反应谱拟合很好．上述对比分析说明了利用本文方法生成的地震动加速度时程具有较高的精度，可以用于工程结构抗震分析．

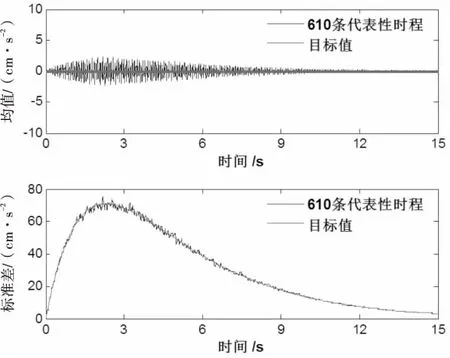
图4 610条代表性时程二阶统计值与目标值比较

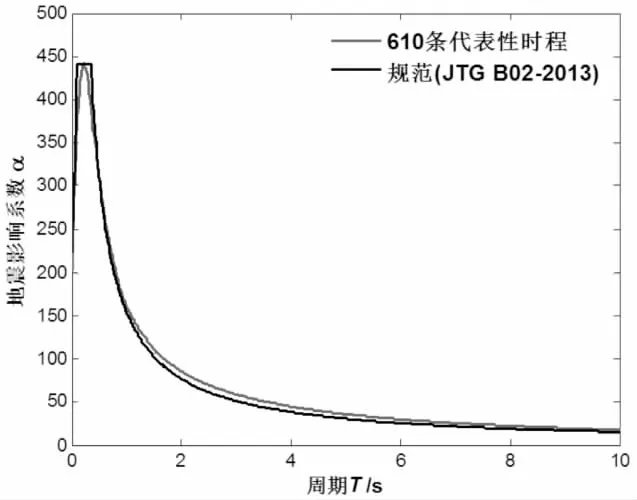
图5 平均反应谱与规范反应谱的比较

4 范和港跨海斜拉桥抗震分析

由于非平稳地震动随机过程的谱表示-随机函数方法生成的地震动加速度时程具有给定的概率信息，且所有的代表性时程构成一个完备的概率集，因而可结合概率密度演化理论对范和港跨海大桥的随机地震响应及抗震可靠度进行精细化的分析．

范和港跨海大桥的基本参数如下[17]，桥梁跨径(52.5+99.5+300+99.5+52.5)=604 m，桥面宽26.9 m，采用双塔单索，塔高28.31 m．主梁采用C55混凝土，截面形式为单箱三室三角箱型，横隔梁间距为6 m，箱梁底板厚度为25 cm，顶板为27 cm．索塔为独柱塔型，顺桥和横桥向分别宽6.9 m和3.4 m，顺桥向1.5 m，横桥向壁厚0.8 m至1.1 m，索塔采用C60混凝土．主塔与主墩刚接，主墩为圆端形截面，长端沿顺桥向为13.8 m至15 m，短端沿纵桥向为5.8 m至7 m，壁厚1 m至2 m．全桥设23对一共184根斜拉索，采用8种规格拉索，从PES(FD)7-109到PES(FD)7-211，拉索最小倾角约为24度，梁上索距为6 m，横向2.2 m，塔上竖向索距为1.6 m，横向为0.8 m．采用有限元软件Midas Civil对范和港斜拉桥进行有限元建模，如图6所示．

图6 范和港大桥有限元模型

采用多重Ritz向量法对桥梁结构进行模态分析以获取桥梁结构的自振频率和各阶振型，限于篇幅，仅列出部分模态，见表2．

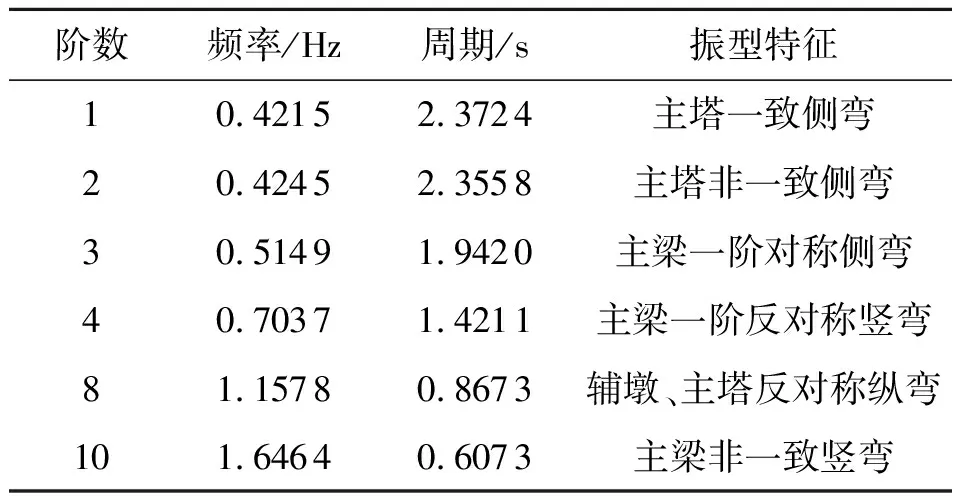
表2 结构部分动力特性

从表中可知：该斜拉桥结构的基频为0.421 5 Hz，对应的振型为主塔一致侧弯，这是因为索塔、主梁、主墩采用了固结形式，有很大的整体刚度；且前三阶模态的振型均表现为主塔侧弯，说明桥塔的横向刚度很小；结构的频谱较为密集，振型分布均匀，尤其高阶振型表现为明显的相互耦合作用．

值得说明的是，式(1)所定义的谱表示模拟公式仅适用于一维单变量随机过程，其模拟结果只能获得单点地震动输入，同时为简化计算，本文仅考虑一致激励下的桥梁结构抗震分析，不考虑地震动的多维相关性以及空间变化特性．将采用本文方法生成的610条代表性时程输入到结构有限元模型中进行确定性的动力时程分析，并结合概率密度演化方法，考虑纵向+横向和纵向+竖向两种地震输入方式，对范和港跨海大桥的非线性地震响应及抗震可靠度进行精细化的分析．方向组合采用SRSS方法，其中水平向地震加速度峰值为0.2g，竖向地震加速度峰值取水平向的0.6倍．限于篇幅，本文仅给出纵向+横向地震输入方式下主墩墩底弯矩响应的二阶统计量和典型时刻的概率信息，如图7所示，从图中可以看出，桥梁结构在地震作用下产生强烈的非平稳响应，且主墩墩底弯矩不同时刻的典型概率密度曲线表现出明显的随机性特点．

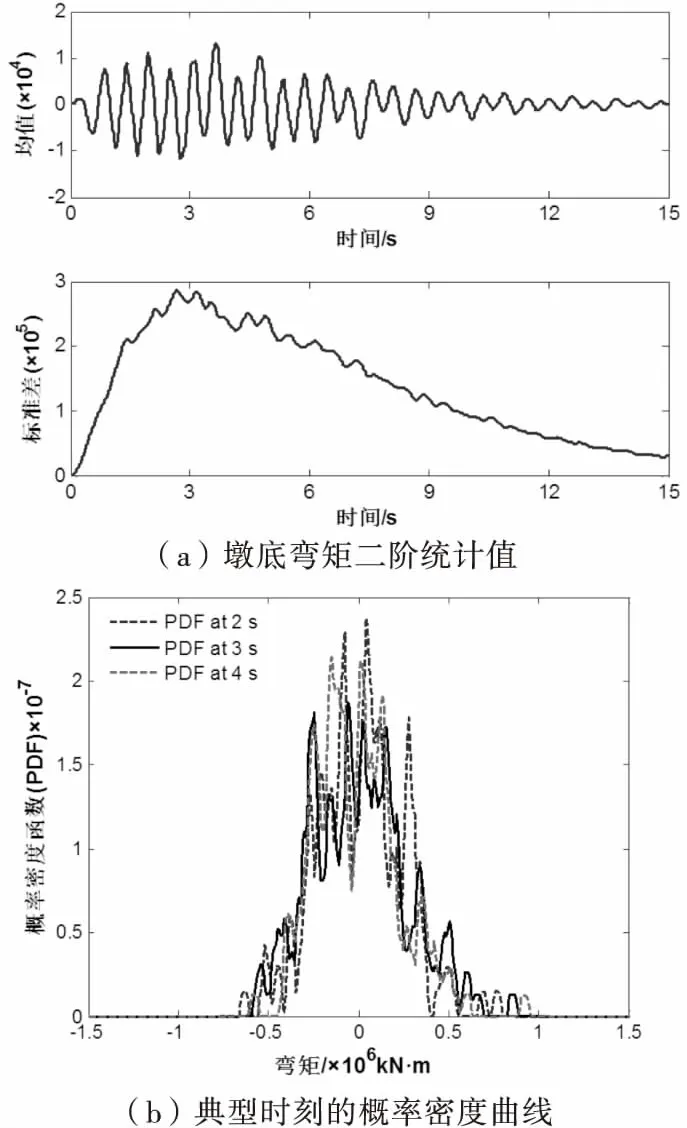
图7 结构地震反应的概率信息

在上述桥梁结构非平稳地震动响应分析的基础上，结合等价极值事件的思想[12]，分别取主墩墩底的轴力和弯矩作为可靠度评价指标，对桥梁结构抗震可靠度进行定量的评价．根据大量的震害资料，分别选取可靠度阈值为1.8×104kN和1.0×106kN·m．图8为纵向+横向和纵向+竖向地震输入方式下的桥梁抗震可靠度计算结果，从图中可以看出，当采用轴力作为可靠度指标时，纵向+横向和纵向+竖向地震输入方式下的可靠度分别为100%和65%；当采用墩底弯矩作为可靠度指标时，两种地震输入方式下的可靠度曲线几乎重合，且抗震可靠度均为100%，这说明横向地震激励和竖向地震激励对主墩墩底弯矩的影响是一致的．对比图8(a)和图8(b)可以发现，对于同一失效阈值，轴力在纵向+竖向地震输入方式下的可靠度远小于纵向+横向地震输入的抗震可靠度，这说明竖向地震激励对墩底轴力的可靠度有较大的影响，其抗震可靠度明显不满足，因此在桥梁结构抗震设计中需重点考虑竖向地震激励对主墩墩底轴力的影响．

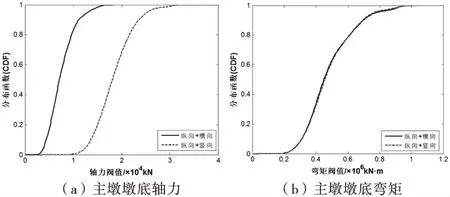
图8 结构抗震可靠度

5 结 论

本文在平稳地震动过程的Kanai-Tajimi功率谱基础上，建议了一类时-频非平稳地震动演变功率谱模型，结合《公路工程抗震规范》(JTG B02-2013)和非平稳过程模拟的谱表示-随机函数降维方法，生成了与规范反应谱相一致的地震动加速度代表性时程集合．利用 有限元软件建立斜拉桥有限元模型，对桥梁非平稳地震响应进行了概率密度演化分析．在此基础上，结合等价极值事件的思想，分别选用主墩墩底轴力和弯矩作为可靠度评价指标，对桥梁结构抗震可靠度进行了精细化的分析．研究结果表明，地震动随机过程的时-频非平稳演变功率谱模型能够充分体现强度和频率非平稳特性，且该模型与规范结合紧密，从而可以方便地用于工程实践．对范和港跨海大桥的抗震分析表明，竖向地震激励对墩底轴力的可靠度有较大的影响，因而在进行桥梁设计时需重点考虑竖向地震激励对主墩墩底轴力的影响．