几种空间谱估计测向算法的比较
2018-10-15朱肃娴
朱肃娴
(中国船舶重工集团公司第七二三研究所,江苏 扬州 225001)
0 引 言
阵列信号处理的一个重要应用是在空间谱估计测向中的应用,而空间谱估计测向在雷达、通信等很多方面有着极其广泛的应用。介绍常用的空间谱估计算法,包括MUSIC算法、ESPRIT算法及改进算法,并进行仿真分析,比较其优缺点,以期为装备科研生产提供理论依据。
1 空间谱与DOA估计
对于均匀线阵,当空间仅有一个信号源且不考虑信号噪声时,均匀线阵接收到的信号可表示为:

定义xm(n)的空间傅里叶变换为:

因为:

所以:

|x(φ)|2常称为空间谱。当φ=φ1时,式(4)取得最大值。因此,可以通过搜索|x(φ)|2峰值位置,利用φ1=2πdsinθ1/λ来确定信号源的方向。
2 空间谱估计测向
空间谱估计测向系统的原理[1]:空间谱估计测向采用信号来波在每个天线阵元上感应产生电压信号幅度和其信号相位,与来波方向相关对应特性而实现对空间多个信号同时测向。空间谱估计测向应用多元天线阵,如图1所示。

图1 空间谱估计测向系统组成
空间谱估计测向系统设计[2]:实现空间谱估计测向系统应具备物理支持(天线阵列和数字接收机)和软件系统支持。硬件和软件两者应相辅相成,硬件的高能性、一致性可以减小采样数据的误差,可以很好地表现软件的超分辨性能。
3 经典空间谱估计算法
3.1 MUSIC算法
3.1.1 算法原理
假设空间远场信号源共有D个,各信号互不相关,各阵元噪声nm(t),m=1,…,M也互不相关,噪声与信号Sk(t),k=1,…,D也不相关[3]。
第m个阵元的输出结果为:

式中:

θk为k个信号的到达方向(线阵的法向为0°),d为阵元间隔,λ为信号工作波长。
将式(5)(共M个方程)写成矩阵方程,有:

其中:

求各阵元输出的空间相关矩阵,有:

式中:

其中,E{·}为求期望值,T为转置,H为复共轭转置,σ2为噪声的方差。
对R进行特征值分解,并将其特征值按降序排列,可以得出下面关系:
(1)特征值 λ1≥ λ2…λD> λD+1=…=λM;
(2)特征向量 V1、V2…VD、VD+1、VM。
进一步分析,得如下结果:
(1)R的最小特征值等于σ2,重数为M-D,即:

据此空间信号源的数目,可立即估计出来:

最小重数为1。因此,M元阵可同时侧向的信号数目的最大值为:

(2)矩阵R列空间的基是各相互正交的向量,ΩN为其中噪声特征的子列空间项,Ωs为其中信号序列的子列空间,是由除最小特征值以外的特征值对应的特征向量形成的子空间。在信号源所在方向上,诸方向向量a(θk),k=1,…D均处在信号子空间Ωs中。因此,构造矩阵:

显然,有:

MUSIC算法就是根据式(19)求空间谱PMU(θ),有:

式中 ||·||2表示向量的 2范数,PMU(θ)峰值所对应的θ值是信号源方向的估值[4]。
3.1.2 Matlab仿真
输入信号:输入三个不同频率(即就是不相关信号)的复信号,频率分别为1 100 Hz、1 300 Hz和1 500 Hz,阵元数目为8,采样频率为5 000 Hz,信源入射角度分别为20°、30°和45°。输出结果分别如图2、图3、图4所示。

图2 信噪比SNR=0 dB,快拍数L=2 048的MUSIC算法仿真

图3 信噪比SNR=20 dB,快拍数L=2 048的MUSIC算法仿真

图4 信噪比SNR=20 dB,快拍数L=128的MUSIC算法仿真
对于图2,信噪比SNR=0 dB,快拍数L=2 048,测向结果为20.007 9、30.149 2和45.160 7。
对于图3,信噪比SNR=20 dB,快拍数L=2048,测向结果为20.065 2、30.034 7和45.046 2。
对于图4,信噪比SNR=20 dB,快拍数L=128,测向结果为20.179 8、30.149 2和45.046 2。
通过对比可得,对于MUSIC算法,相对于快拍数的影响,信噪比的影响更明显。由本算法的原理可知,该算法的缺点在于不能够区分相干信号的信号源方向。
因此,为解决相干信号的处理问题,通常采用两种算法:
(1)通过牺牲一定有效的阵元数量,使信号具有不相干性,即通过预处理使天线接收到的阵列信号失去相干性,然后应用相关算法获得精确的到达角。相关算法包括前后向预测投影矩阵方法、空间平滑方法和数据矩阵分解方法。
(2)应用移动阵列的方法或应用频率平滑的方法处理相干信号,但是不损失阵元数,应用结合去相干与空间谱估计方法处理。此算法包含频率平滑方法和旋转不变子空间算法。
下面对常用的两种算法(旋转不变子空间算法和前向空间平滑算法)进行应用仿真,并比较其优缺点。
3.2 前向空间平滑算法
3.2.1 前向平滑
众所周知,均匀线阵(ULA)算法(如图5所示)具有的特性是平移的固定性,所以将这个阵列采用相关特性可分化为与其互相重叠的L个分子阵列,然后它们相互关联的每个子列阵中的阵元数量为m=M-L+1,且每个子列阵包含同一个信源方位的信息。下面按照多重信号分类算法计算这L个子列阵的自协方差矩阵,计算它们的算术平均值,然后形成一个相对等效的m阶子列阵列的协方差矩阵Rf[5]。

图5 平滑空间的计算方法的示意图
对协方差矩阵方法求得的数值做特征值分解处理构造噪声子空间,根据正交性估计信源方向。可以看出,若m>D且L≥D时,经过其子阵平滑的m阶对应的信源协方差矩阵的秩恢复为D。另外,空间平滑技术的缺点是由于子阵列比原阵列小导致阵列有效孔径减小。
3.2.2 Matlab仿真
输入信号:输入为两个频率为1 000 Hz的相干信号,采样频率为2 000 Hz,阵元数目为8,快拍数为1 024,信源入射角度分别为-30°、45°,信噪比为20 dB。
输出结果:分别输出子阵个数为1、2、3、4、5、6、7、8,对应子阵阵元数为8、7、6、5、4、3、2、1时,测向结果分别如图6、图7、图8、图9、图10、图11、图12、图13所示。

图6 L=1,m=8的前向空间平滑算法仿真

图7 L=2,m=7的前向空间平滑算法仿真

图8 L=3,m=6的前向空间平滑算法仿真

图9 L=4,m=5的前向空间平滑算法仿真
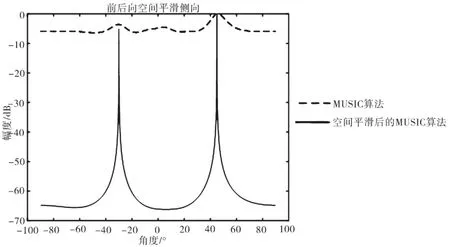
图10 L=5,m=4的前向空间平滑算法仿真
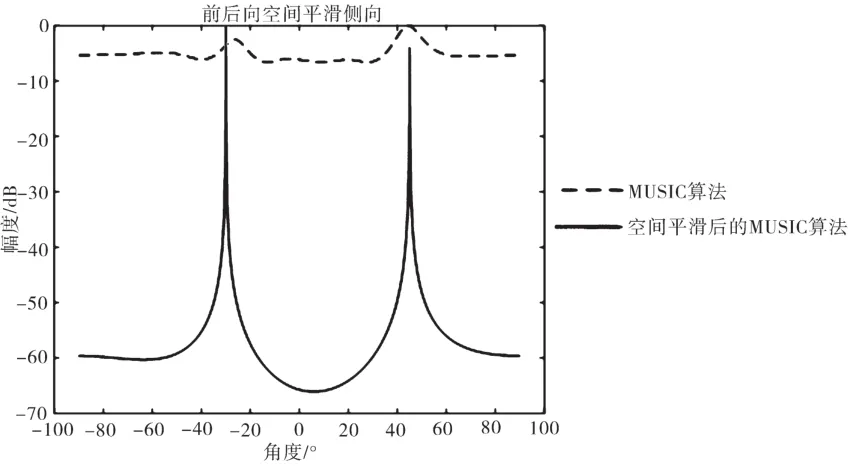
图11 L=6,m=3的前向空间平滑算法仿真

图12 L=7,m=2的前向空间平滑算法仿真
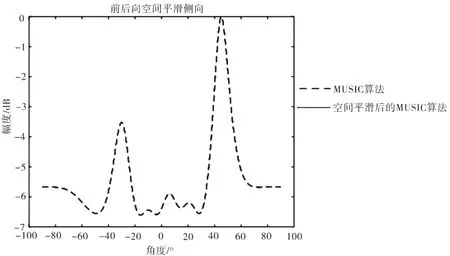
图13 L=8,m=1的前向空间平滑算法仿真
结论:当信源数<子阵阵元数且信源数≤信源数时,可以准确测量经过前后向平滑阵列协方差矩阵的信源数个相干信源。缺点在于,算法原理决定了该算法不能区分特别近情况下的相干信号[6]。
3.3 旋转不变子空间算法
3.3.1 旋转不变子空间算法原理
旋转不变子空间算法包含MUSIC算法和ESPRIT算法,都是对阵列接收数据协方差矩阵进行特征分解。虽然这两种算法采用的特征分解特性不同,但是两种算法可以互为补充进行计算。
假设存在两个一样的子阵,且每个子列阵Δ确定,有着相同的信号,每个子阵列释放的信号相位差Φ(i=1,2,…N)。
假设两个子阵的第一个接收数据是X1,其中另外一子阵的收获数据是X2,按照上述所述阵列的数学模型可以获知:

式中,N1、N2为M-1维度的噪声矢量代号;S为空间信号的N×1维度的信号矢量代号;A为阵列的M×N维度的流型矩阵。
其中:

根据Φ对角阵,根据公式可以简化矩阵如下:

可以发现,要能够获得到达角信号,只要得到每个子阵列关系的旋转不变关系Φ。
下面只需从式(21)和式(22)中得到每个子阵列之间的关系。具体地,需要先将这两个子阵列模型合为一,如下:

理想状况下,计算出X协方差矩阵的R:

特征分解,得:

可以得到这些特征值之间的相互关系为:

再根据快速拍摄获得的数据,对式(27)进行修正得到结果:
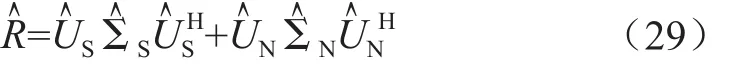
于是,有:

根据只有一个非奇异矩阵T,得出:

得出的结构对每个子阵列都是可以应用的,如下:

可以发现,US1=US2=A,即有:

再根据阵列流型在每个子阵列上如下的关系:

采用式(31)计算这两个子阵间对应的信号子空间有如下关系:
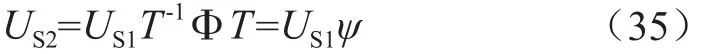
若US1满秩,则具有唯一的解释,可以得出:

然后特征分解:

式中ψ的特征值对应构成其对角阵在数值上和Φ一定等同,且ψ特征矢量是矩阵的各列。因此,可以获得旋转不变关系矩阵ψ,然后可以应用公式得信号的来源。
3.3.2 Matlab仿真
输入信号:输入为两个频率为1 000 Hz的相干信号,采样频率为2 000 Hz,阵元数目为8,快拍数为1 024,子阵数为4,信源入射角度分别为-45°、30°、60°,信噪比为20 dB。
输出结果,如表1所示。

表1 旋转不变子空间算法仿真
4 结 论
空间谱测向中两种典型的算法——MUSIC算法和旋转不变子空间(ESPRIT)算法。对阵列接收数据协方差矩阵进行特征值分解,是这两种算法的相同点。MUSIC算法和旋转不变子空间(ESPRIT)算法差异是采用特制分解的特性不同,且它们之间不是相互独立的。MUSIC算法的改进方法是使用前向空间平滑算法,使其可以适用于相干信号源。以上算法通过仿真验证可以看出,采样率、快拍数、信号的相干性都对测向有一定影响。
通过仿真分析可以看出,MUSIC算法和ESPRIT算法主要采用了接收数据协方差矩阵的噪声子空间的正交特性和旋转固定性(计算量小,不需要进行谱峰搜索)。实际工程中,可根据对应的信号相关性、测向分辨率的要求及硬件约束来选择恰当的谱估计算法。
