基于遗传算法的潮流能水轮机叶片翼型优化设计研究❋
2018-10-15王旭超王树杰谭俊哲司先才边冰冰
袁 鹏, 王旭超, 王树杰, 谭俊哲, 司先才, 边冰冰
(1.中国海洋大学工程学院,山东 青岛 266100; 2. 山东省海洋工程重点实验室,山东 青岛 266100)
叶片是潮流能水轮机直接承受水动力并将其转化为机械能的部件,其性能对潮流能水轮机的获能效率有重要的影响。而叶片的水动力学性能与叶片各剖面的翼型密切相关[1]。因此,开发适合潮流能水轮机性能要求的专用翼型对提高潮流能水轮机的获能效率有重要意义。
目前,对翼型的研究多集中在飞行器和风力机领域。飞行器上应用的主要是美国国家航空航天局(NASA)开发的NACA系列翼型,如NACA44系列、NACA63-2系列、NACA64-4系列等。为了适应风力机的运行特点,从1980年代开始,一些风电技术发达的国家相继开始了风力机专用翼型的研究,并取得了显著的成果。现在应用比较成熟的风力机翼型主要包括美国可再生能源实验室开发的NREL-S系列翼型[2]、荷兰代尔夫特工业大学(Delft university of technology)发展的DU系列翼型[3]、丹麦RIS国家重点实验室开发的RIS系列翼型[4]以及瑞典航空研究院(FFA)开发的FFA-W系列翼型[5]等。近几年,国内一些科研单位和科研院校也陆续开展了对风力机专用翼型技术的研究,并且开发出了具有自主知识产权的风力机专用翼型,主要包括中国科学院工程热物理研究所开发的CAS-W系列翼型[6]、西北工业大学开发的NPU-WA系列翼型[7]、重庆大学设计的CQU-A系列翼型[8]等。
近年来,国内外相关学者针对潮流能水轮机翼型开展了相关研究,Goundar等采用数值模拟和试验方法对HF-Sx、Fx63137、以及NACA63815翼型进行了升阻特性对比[9];英国南安普顿大学的Bahaj等对水平轴海流能发电机叶轮及叶轮翼型进行了大量的试验及测试工作[10];Grasso利用RFOIL软件和序列二次规划法相结合开展了翼型优化设计[11];Molland等利用XFOIL软件对二维水翼的空泡问题进行了研究[12]。任毅如、张田田等人基于遗传算法建立了水轮机翼型优化设计模型,并用XFOIL软件对翼型的水动力学性能进行了评估[13];朱国俊、冯建军等人采用RBF神经网络与NSGA-Ⅱ相结合的现代优化技术对潮流能水轮机的多工况优化问题进行了研究[14];王俭超等人用CFD软件Fluent对多种NACA系列翼型进行了数值模拟研究,获得了翼型的水动力特性曲线[15]。这些研究极大地促进了潮流能水轮机翼型技术的发展,本文在上述研究的基础上,开展了潮流能水轮机翼型的优化设计研究工作。
NACA4418翼型具有阻力系数小、最大升力系数高、扭距低等特点,在一些风力机和潮流能水轮机中得到了应用[16],因此本文以NACA4418翼型为初始翼型,对初始翼型进行参数化拟合,确定目标函数、设计变量和约束条件,通过遗传算法找到最优解后,采用数值模拟的方法对初始翼型和优化翼型进行水动力学分析,并讨论、分析数值模拟结果。
1 潮流能水轮机翼型设计要求
目前,在潮流能水轮机叶片上主要应用的是航空翼型和风力机翼型,但是潮流能水轮机的工作介质、工作条件与飞行器和风力机有很大区别,本文将从潮流能水轮机翼型与航空翼型及潮流能水轮机翼型与风力机翼型的区别方面来讨论潮流能水轮机翼型的设计要求。
1.1 潮流能水轮机翼型与航空翼型的区别
潮流能水轮机翼型与航空翼型的主要区别在于以下几个方面:
(1)飞行器主要是在高空条件下运行,所以航空翼型是按表面光滑设计的;由于海水中浮游生物的附着会导致潮流能水轮机叶片表面变粗糙,所以在潮流能水轮机翼型设计过程中,必须考虑粗糙度敏感性对潮流能水轮机翼型水动力学性能的影响。
(2)飞行器处于失速状态时,会导致坠机的危险,所以航空翼型在设计过程中应尽量避免其处于失速状态;而大攻角会引起流体与潮流能水轮机叶片翼型的分离,升力剧烈下降,导致水轮机的振动[17],因此潮流能水轮机翼型要具有良好的失速特性。
(3)飞行器一般在高空条件下运行,高空空气比较稀薄对叶片的冲击较小,所以航空翼型的最大相对厚度一般不超过20%;而潮流能水轮机处于海水运行条件下,海水对叶片的冲击要比高空稀薄的空气大的多,为了保证潮流能水轮机叶片的结构和刚度要求,叶片根部翼型的厚度一般都比较大,有时最大相对厚度甚至达到40%以上[18]。
1.2 潮流能水轮机翼型与风力机翼型的区别
潮流能水轮机翼型与风力机翼型的主要区别在于以下几个方面:
(1)风力机叶片一般都比较细长,叶片旋转过程中会产生较大的扭转力矩,所以力矩系数是风力机翼型设计过程中必须需要考虑的一个重要参数;而潮流能水轮机叶片一般都比较刚硬,力矩系数并不是潮流能水轮机翼型设计过程中考虑的关键因素。
(2)由于风速比较大,并且风向和风速变化都比较频繁,在风力机翼型设计过程中,一般选择较高的设计升力系数来降低疲劳载荷和阵风载荷;而潮流能水轮机所处的流场环境湍流度较低、流速和流向都具有较强的规律性,所以疲劳并不是潮流能水轮机翼型设计过程中考虑的主要因素。
(3)风力机所处的运行环境,一般风速都比较大,并且变化频繁,风力机经常在失速区运转,所以在风力机翼型设计过程中,失速点的设计非常重要。而潮流能水轮机所处的运行环境,虽然也会出现失速现象,但流速和流向具有较强的规律性,翼型失速点的设计并不是潮流能水轮机翼型设计过程中考虑的关键因素。
2 潮流能水轮机翼型设计方法
目前,常用的翼型优化设计方法主要有正问题设计法和反问题设计法[19]。反问题设计法一般是以速度分布、压力分布为目标参数,通过迭代求解几何和流动控制方程来达到目标的速度和压力分布。这种方法难以处理多学科问题,并且翼型的控制点很难确定。正问题设计法以数值优化方法为基础,对初始翼型不断进行几何修形,直至达到目标升力或升阻比,这种设计方法可以改善多个设计参数并施加多种约束,随着计算机技术的发展,正问题设计法得到了广泛发展。
本文以在潮流能水轮机叶片上常用的NACA4418翼型为初始翼型,采用正问题设计法进行翼型的优化设计。用儒可夫斯基保角变换的方法对初始翼型进行参数化拟合,确定目标函数、设计变量和约束条件,通过寻优算法寻找最优解,找到最优解后,对初始翼型和优化翼型进行水动力学分析,并比较分析结果。具体的设计流程见图1。
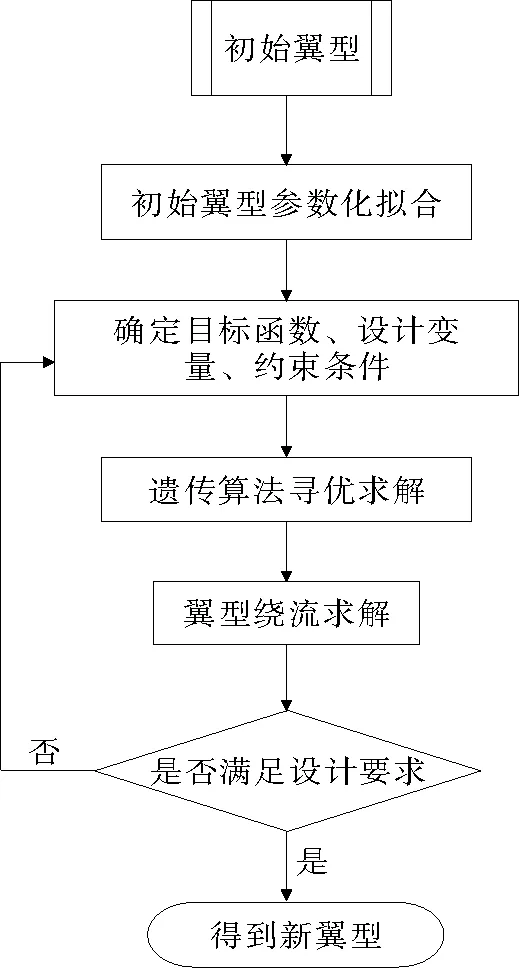
图1 翼型设计流程图 Fig.1 Flow chart of the hydrofoil design
3 潮流能水轮机翼型优化设计模型的建立
3.1 翼型的参数化建模
翼型参数化方法的优劣对翼型的设计效果有重要影响,它是决定翼型设计效率和翼型水动力性能的关键因素。本文选用基于儒可夫斯基保角变换的方法对潮流能水轮机翼型进行参数化表达。
利用儒可夫斯基保角变换式[20]:
ζ=f(x)=z+e2/z。
(1)
就可以将z平面上的一个圆变换为ζ平面上的一个翼型。其中e表示1/4翼型弦长。
ζ平面上的翼型在笛卡尔坐标系下就可以表示为:
(2)
其中:l表示翼型的矢径长度,将其表示为θ的函数:
l=e·exp(φ(θ))。
(3)
根据Taylor级数对的思想,将φ(θ)展开为:
φ(θ)=m1(1-cosθ)+n1sinθ+m2(1-cosθ)2+
n2sin2θ+L+mk(1-cosθ)k+nksinkθ+L,
k=1,2,3,L
(4)
从公式(4)可以看出当θ=0时,φ(θ)=0,从而保证了翼型的尖尾缘特性。通过mk、nk的不同取值就可以得到不同的翼型。
3.2 目标函数
潮流能水轮机叶片设计的主要目标是使潮流能的功率系数CP达到最大,而CP通常是通过叶素理论来进行计算。
选取距叶片旋转中心距离为r处的叶素进行研究,叶素上速度与受力分布见图2。虚线为叶素所在的旋转平面,V为来流速度,U为水流相对于叶素的合成来流速度,α为来流攻角,Ф是入流角,β为叶素扭角,c叶素弦长。
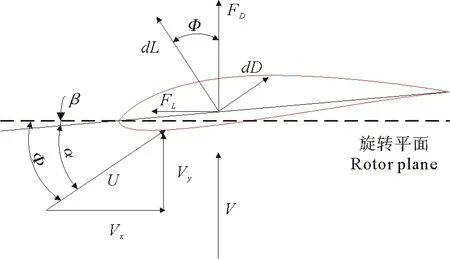
图2 叶素速度与受力图Fig.2 Blade element velocity and load diagram
合成来流速度U为平行于旋转平面的切向速度Vx与垂直于旋转平面的法向速度Vy的合成速度,其中:
Vx=Ucosφ=(1+a′)Ωr。
(5)
式中:Ω为水轮转动角速度。
Vy=Usinφ=(1-a)V。
(6)
而水流流过水轮机产生的升力效应会使水轮机旋转做功,水流的轴向速度减小,并产生切向旋转速度。定义a为轴向诱导因子,a′为切向诱导因子,分别表示水流轴向与切向速度的变化量,在稳态运行情况下,a、a′存在稳定值[21]:
(7)
式中:λ为局部尖速比,为距旋转中心r处的叶素旋转速度与水流速度之比,即
(8)
根据库塔儒可夫斯基升力方程可以推导出叶素微元的升阻力为:
(9)
(10)
为了使单个叶素的升、阻力的比值最大,即dL/dD最大,有公式(9)、(10)可知:
(11)
式中:CL为升力系数;CD为阻力系数。
由公式(11)可知要想使叶素的升、阻力的比值达到最大,就需要保证升阻比(CL/CD)最大,因此确定目标函数为:
f(X)=max(CL/CD)。
(12)
3.3 设计变量
为了完整的表达翼型,同时减少计算量,本文选择公式(4)中φ(θ)的前6项作为优化设计变量,记作:
X=(x1,x2,x3,x4,x5,x6)。
(13)
3.4 约束条件
本文是针对NACA4418翼型进行优化,其最大相对厚度为18%,即施加约束:
t/c=18% 。
(14)
式中:t为翼型的最大厚度;c为翼型的弦长。
NACA4418翼型的最大厚度所在的弦向位置在距前缘30%处,为了保证优化翼型的几何兼容性,施加约束:
Lmax=0.30。
(15)
考虑到翼型的强度要求,需要对它的截面积进行约束:
(16)
式中:S为优化翼型的截面面积;S0为初始翼型的截面面积。
减小翼型的前缘半径可以使转捩点位置前移[22],从而保证光滑和粗糙条件下翼型的转捩点位置基本相同,减小翼型的前缘粗糙度敏感性。因此,需要对翼型的前缘半径进行约束:
Le≤3% 。
(17)
潮流能水轮机作为一种大型旋转类机械,需要对其进行降噪处理,而翼型尾缘是主要的噪声来源,根据翼型噪声预测理论,其尾缘噪声随着尾缘厚度的增加而增大,因此,需要对翼型尾缘厚度进行约束[23]:
yu,1-yl,1≤0.01。
(18)
式中:yu,1—x=1时翼型上表面的y坐标值;yl,1—x=1时翼型下表面的y坐标值。
增大翼型最大相对弯度可以提高翼型的升力系数和升阻比,因此本文对最大相对弯度进行约束:
4%≤w/c≤6% 。
(19)
其中:w为翼型最大弯度;c为翼型弦长。
翼型的最大相对弯度所处的弦向位置愈靠近翼型后缘,其升力系数愈高、阻力系数愈低、升阻比愈大,因此,需要对最大相对弯度所处的弦向位置进行约束:
45%≤Lw≤50% 。
(20)
3.5 优化设计程序
遗传算法作为一种现代优化方法,借鉴了达尔文的进化论和孟德尔的遗传学说,其本质上是一种高效、全局搜索的方法[24]。本文采用遗传算法进行翼型的寻优求解,以期获得全局最优解。该算法从一组初始种群开始求解,每一组解都采用二进制形式进行编码,选择一个适应度函数,对每一个解的适应度进行评估,选出适应度好的个体进行选择、交叉、变异,最后选出最优个体。其具体的优化求解过程见图3。
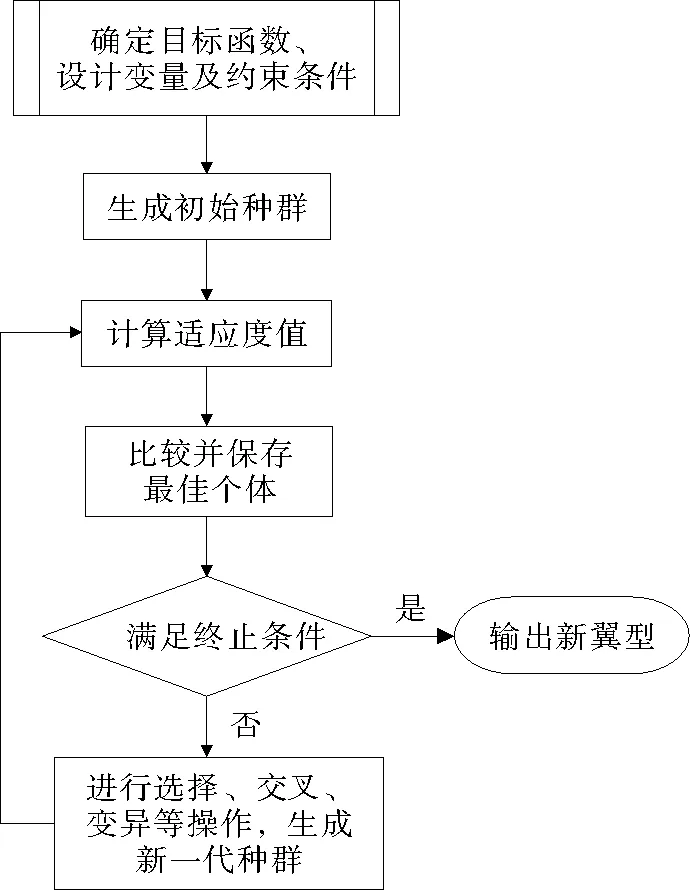
图3 翼型优化设计流程图Fig.3 Flow chart of the hydrofoil optimization and design
4 优化结果及结果分析
4.1 潮流能水轮机翼型优化结果
本文以NACA4418翼型为初始翼型,通过在MATLAB中对遗传算法进行编程求解得到了一种新的翼型,图4为初始翼型与优化翼型的形状对比。优化后的翼型上翼面变厚,下翼面变薄翼型的弯度更大。
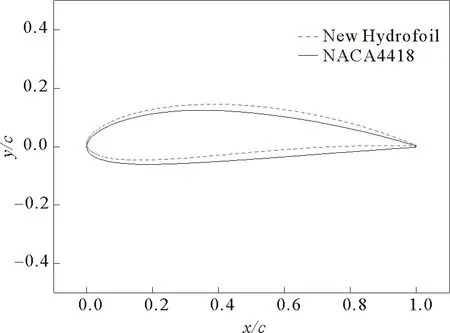
图4 初始翼型与优化翼型的形状对比图 Fig.4 Comparison diagram of the initial hydrofoil and optimized hydrofoil
4.2 潮流能水轮机翼型的水动力学分析
优化后的翼型需要进一步通过水动力学来确定其优化效果,目前常用的翼型动力学分析方法主要有两种,一种是把粘性和无粘性相结合考虑的涡面元法,另外一种是CFD求解N-S方程的方法。
基于涡面元法和边界层理论开发的XFOIL软件,被广泛应用于翼型的设计和分析,并且用en法来预测转捩点的位置,对薄翼型、小攻角的翼型水动力学分析准确性较高,但是在大攻角和翼型厚度比较厚的情况下准确性降低。
CFD软件Fluent被广泛应用于流体的动力学分析,它不仅能准确预测翼型的水动力学性能,而且能得到一些相关的流场信息。
本文采用CFD软件Fluent进行翼型的水动力学分析,其分析的关键是对翼型进行网格划分。本文用Gambit软件进行网格划分,采用了C型结构化网格,对翼型周围进行局部加密处理,翼型网格结构见图5。
在Fluent求解计算过程中假定来流速度1.5 m/s,通过改变x、y方向上的速度大小来计算-5°~25°攻角下的升、阻力系数。Standard k-ε湍流模型对二维翼型绕流数值计算具有较高的准确性,尤其是对于大攻角分离流动的计算精度高[25],因此湍流模型选用Standard k-ε两方程湍流模型。

图5 NACA4418翼型整体网格图和网格局部放大图Fig.5 The whole grid diagram and the grid partial enlargement diagram of NACA4418 hydrofoil
4.3优化结果分析
通过CFD软件Fluent的迭代求解计算,得到NACA4418翼型和优化翼型在不同攻角下的升力系数曲线及升阻比曲线,见图6、7。

图6 NACA4418翼型和优化翼型升力系数对比图Fig.6 Lift coefficient comparison diagram of NACA4418 and the optimized hydrofoil
从图6可以看出优化后的翼型,在整个攻角范围内,都比初始翼型拥有更大升力系数。优化后的翼型最大升力系数达到了1.017 8,相比于初始翼型的0.863 5提高了17.87%;并且,优化翼型具有更缓和的失速特性。
从图7可以看出优化后的翼型相比于初始翼型在整个攻角范围内都拥有更高的升阻比。优化后的翼型最大升阻比达到了15.351 3,相比于初始翼型的10.489 2提高了46.35%。
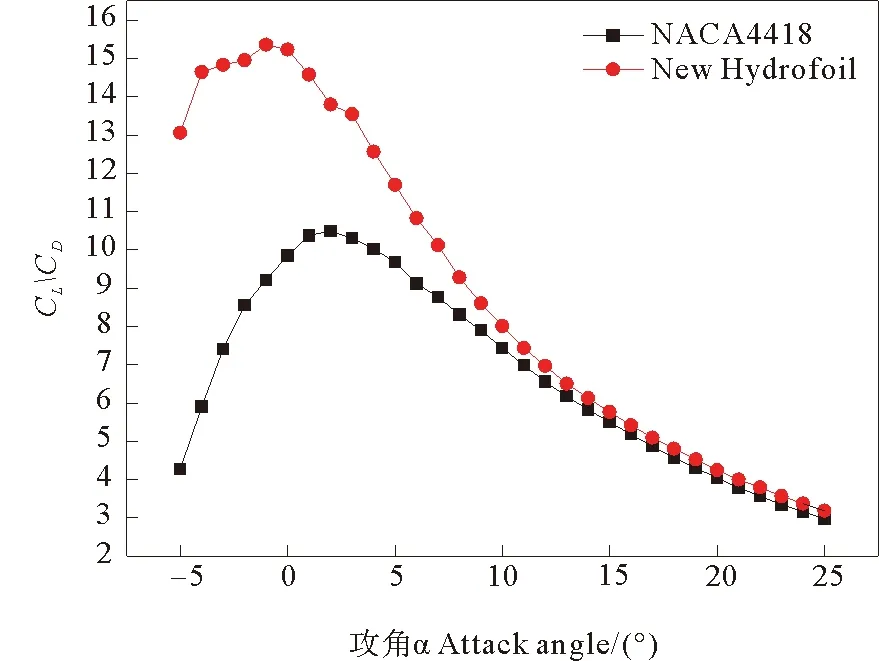
图7 NACA4418翼型和优化翼型升阻比对比图Fig.7 Lift-to-drag ratio comparison diagram of NACA4418 and the optimized hydrofoil
由此可见,优化后的翼型拥有更佳的水动力学性能,有利于潮流能水轮机获能效率的提高。
5 结论
通过分析潮流能水轮机翼型与航空翼型的区别以及潮流能水轮机翼型与风力机翼型的区别,提出了潮流能水轮机翼型的设计要求,为潮流能水轮机翼型的设计提供了借鉴。
采用儒可夫斯基保角变换的方法对翼型进行参数化表达,实现了翼型表达完备性和可控性的要求,并且保证了尖尾缘特性,为后续的翼型设计、研究提供了理论基础。
采用遗传算法进行全局寻优求解,通过设定多个约束条件来实现翼型的多种设计要求。求解出最优解以后,通过CFD软件Fluent进行潮流能水轮机翼型绕流数值计算,验证了优化翼型相比于初始翼型拥有更高的升阻比,证明了该翼型设计方法的可行性。
