基于萤火虫算法的磁信标自主定位方法

刘超越，王 冠，夏红伟，马广程，马广生，王常虹

(哈尔滨工业大学，哈尔滨 150080)

0 引言

传统定位和跟踪应用如雷达和全球定位系统(Global Positioning System，GPS)，受到天气和地域的限制，无法适应水下、室内和地下等应用场合。因此，利用其他的信号源进行定位的研究应运而生。

在一些特殊的应用领域，基于磁信标定位方法具有其他定位导航方式无法取代的重要地位。低频准静态磁场可穿透土壤、岩石、海水、建筑物和许多其他类型的介质，不受恶劣的天气条件或昼夜变化的直接影响，在许多室内和室外的应用十分方便。准静态磁场的应用包括定位、通信、磁场监测、地震预测研究等等。特别是相对于传统定位和跟踪应用需要视线来进行有效的操作，如声纳和雷达。而低频磁信标定位则不需要视线来进行操作，所以在许多室内和室外的应用十分方便。例如许多救援行动同样应用了低频磁场，对被困矿工进行定位。在上述的应用中需要多点测量，在某些情况下是无法实现的。它们可以被归类为地下位置的定位方法。

2010年，美国 Dr. Clay Davis 等仿照 GPS 定位原理，利用3个以上的磁信标，通过计算目标点与3个磁信号源的相对位置关系，根据提前布置的信号源位置，得到目标的绝对位置坐标，并利用卡尔曼滤波技术进行优化。这种方法提供了一种新的利用交变磁场定位的思路，但其研究中没有给出具体解算步骤以及误差方程[1]。

M Diaz-Aguiló等研制了一种利用4个磁线圈构成磁信标定位的系统，应用神经网络算法，对所测量的磁场大小进行一定时间的训练，最后通过估计得出最终目标位置[2-3]。

这些方法已经通过大量的计算机模拟测试，定位结果十分精确。仿真结果可以预测定位精度信标偏差、传感器偏差、接收机仰角、测量噪声等。开发了一套系统原型，包括磁信标和要被定位的接收机。在实际条件下进行实验，验证了仿真结果，并保证了模型的有效性。所提出的方法因精确的结果和简单的实现对许多实时领域的应用具有很强的吸引力。

目前，无论是航空领域、军事领域还是民生方面，利用低频交变磁信号建立磁信标进行定位的方法都存在着广泛的应用前景，因此基于磁信标定位定向系统逐渐受到更多研究者的重视。

本文提出的基于萤火虫算法的磁信标自主定位方法就是一种基于低频准静态磁场的定位方法。通过应用萤火虫算法对标准磁场信息进行匹配，进而得到相关的位置信息。

1 磁信标定位方法

磁信标定位是基于毕奥-萨伐尔定律，该定律揭示了空间位置、电流大小和磁场强度之间的关系。下面先给出毕奥-萨伐尔定律的基本内容。

1.1 毕奥-萨伐尔定律

毕奥-萨伐尔定律：载流导线上的电流元Idl在真空中某点P的磁感度dB的大小与电流元Idl的大小成正比，与电流元Idl和从电流元到P点的位矢r之间的夹角θ的正弦成正比，与位矢r的大小的平方成反比。

毕奥-萨伐尔定律揭示了磁场与空间位置的关系，因此利用这一定律，可以通过测量磁场的大小确定空间的位置。

1.2 磁信标定位原理

分别将2个通入不同频率正弦电流的磁信标放置在原点和(0,-R)处，信标的空间分布如图1所示。

每个磁信标的磁矩方向平行x轴，这样在二维平面内将会产生一个磁场，该磁场由2个线圈产生的独立磁场矢量和组成。每个线圈在此时产生的磁场强度公式如下：

(1)

(2)

H=H1+H2

(3)

其中，M为每个线圈的磁矩大小，r1为磁通门传感器距离信标1的距离，r2为磁通门传感器距离信标2的距离。由于线圈的磁矩是平行x轴的，故可以将矢量式转换成标量式。

信标1和信标2在空间中均根据式(1)产生相应的磁场，两者的磁场强度相互叠加就可以得到总的磁场强度。此时，每一个空间位置都对应了一个相应的磁场强度。

根据上式确定的标准磁场信息的两轴分量与磁通门传感器测量到的磁场强度信息进行匹配，就可以确定磁通门传感器的位置信息。

2 萤火虫定位算法

2.1 萤火虫算法的背景

萤火虫算法(Firefly Algorithm)源于模拟自然界萤火虫在晚上的群聚活动的自然现象而提出。一般来说，荧光素越亮的萤火虫其号召力也就越强，最终会出现很多萤火虫聚集在一些荧光素较亮的萤火虫周围。在人工萤火虫群优化算法中，每只萤火虫被视为解空间的一个解，萤火虫种群作为初始解随机地分布在搜索空间中，然后根据自然界萤火虫的移动方式进行解空间中每只萤火虫的移动。通过每一代的移动，最终使得萤火虫聚集到较好的萤火虫周围，也就是找到多个极值点，从而达到种群寻优的目的。

2.2 萤火虫算法的基本概念及流程

由上文可知，光强度与2个量有着密切的关系：距离与介质对光的吸收系数。为了表示萤火虫之间的吸引力，需要定义萤火虫的相对亮度与绝对亮度的概念。

绝对亮度：对于萤火虫i，初始光强度(r=0处的光强度)定义为萤火虫i的绝对亮度，记作Ii。

相对亮度：萤火虫i在萤火虫j位置上的光强度定义为萤火虫i对j的相对亮度，记作Iij。

萤火虫算法的中心思想在于萤火虫被吸引向其所处的种群中的亮度大于它的萤火虫移动，并根据萤火虫算法的位置更新公式进行位置更新，直到达到设定的寻优精度或者达到指定迭代次数。

将萤火虫算法与实际萤火虫运动规律连接起来的桥梁是：将待优化函数在特定点的函数值抽象为萤火虫在该点的绝对亮度。假设待优化函数是n维的，且在其解空间共有a只萤火虫，则每个萤火虫的位置对应一个由n个自变量组成的向量xi=(xi1,xi2,xi3，…，xin),i=1,2,…,a,该向量代指解空间中一个潜在解，将向量中的值对应代入待优化函数，则得到每个萤火虫的绝对亮度。绝对亮度的大小就可以代指目标函数在该点处的优劣，亮度大就代表萤火虫所代表的潜在解好。即

Ii=f(xi)

(4)

萤火虫亮度i的亮度随着距离以及空气吸收率变化，定义萤火虫i对于萤火虫j的相对亮度为

(5)

其中,Ii为萤火虫i的绝对亮度，γ为光吸收系数，是一个常数；rij定义为萤火虫i与萤火虫j的笛卡尔距离，它是n维的。

两萤火虫之间的吸引力大小是由萤火虫j对萤火虫i的相对亮度决定的，相对亮度越大，吸引力越大。

吸引力:类比萤火虫之间的相对亮度定义，萤火虫之间的吸引力为

(6)

其中，β0为位于光源处的最大吸引力因子，萤火虫i的吸引力，即萤火虫i的最大吸引力。

位置更新：由于被萤火虫j吸引，萤火虫i改变自己的位置向j靠近，i位置更新公式为

(7)

其中，t为算法迭代次数；ε1是由高斯分布、均匀分布得到的随机数，α为随机项系数。由式(7)可知，萤火虫位置更新由三部分组成：萤火虫上一时刻位置、萤火虫之间由于相互吸引产生的运动以及带有特定参数的随机项。

2.3 萤火虫算法在磁信标定位中的应用

基于萤火虫算法的磁信标自主定位方法的基本原理是建立标准磁场信息，与通过磁通门传感器测量到的磁场强度信息进行匹配，得到位置信息。具体流程如下：

萤火虫算法是求解函数最大值的方法，故应用时首先建立目标函数。在磁定位中所建立目标函数如下：

e(i,j)=∑|Bη(measured)-B(i,j)|

(8)

其中，Bη(measured)为测量信息，在编程测试时以一输入常量代替。B(i,j)为所建立的标定函数，输入(i,j)为位置信息，返回值为(i,j)处的磁场强度。

B(i,j)的求解是通过式(1)计算，将位置信息存储在一个数组或者矩阵之中，再将其代入到公式中，得到磁场的x分量及y分量，而e(i,j)在这里取的是分量的二范数的平方。这样就得到了所要求得的标定函数e(i,j)。通过求取e(i,j)的最小值就可以得到位置信息。

萤火虫算法是求最大值的智能优化算法，故e(i,j)应转换为e-1(i,j)，从而将求解最小值的问题转换为最大值的问题。通过求解e-1(i,j)的最大值，就可以得到待求的位置信息。

2.4 基于萤火虫的磁信标定位算法的软件实现

萤火虫算法的具体实施过程为：首先在解空间中随机分布一定数量的萤火虫；根据萤火虫所处位置坐标计算待优化函数的函数值，即绝对亮度；根据吸引力定义计算萤火虫之间的吸引力；根据位置更新进行萤火虫位置的刷新。循环往复，经过有限次迭代之后，萤火虫聚在一起，得到待优化函数全局最优解，实现过程流程图如图2所示。

在应用萤火虫算法过程中，上述公式中的几个参数会对算法快速性以及全局搜索的局部挖掘能力存在较大影响，每个参数对于算法的性能具有特定的影响，所以在本节中将简要介绍每种参数的改变会对算法结果产生怎样的影响。

(1)光吸收系数对算法性能的影响

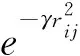
当光吸收系数γ增大时，由于其衰减作用，会使距离对于相对亮度大小的影响程度提高。整个算法在运行过程中，由于临近的萤火虫吸引力要远强于距离远的萤火虫，所以整个种群会分割成多个子种群，每个种群中的萤火虫都朝向自己种群中的局部最优解移动，如此可以保证在最后得到全局最优解之前尽可能多地搜索到局部最优解。

因此，选择合适的光吸收系数可以有效提高效率，并且能够做到平衡算法的全局探测与局部挖掘的能力。

(2)最大吸引力对算法性能的影响

最大吸引力指的是萤火虫在光源处的吸引力，由于该参数的大小选择对于整个种群中所有萤火虫影响相同，相当于同时乘以一个比例系数，所以其对整个算法影响非常小。在实际实践中通常选β0=1。

(3)随机项系数对算法性能的影响

随机项算法对于算法的快速性也具有很大影响，如果随机项系数过大，则会导致新产生的解与上一步得到的解之间相差过大，使得算法随机性太强，破坏算法的规律性；但是同时也能增加算法的全局探测能力，能够使算法进入新的可行解区域。如果随机项系数太小，则算法对于最优解的搜索能力变弱，萤火虫会缓慢向最优解移动，导致算法效率降低。

在算法初期，随机项系数应该较大，用于搜索更多可行域并加快算法速度，而算法后期应该适当降低随机项系数，以防止由于随机项过大导致丢失最优解的情况。

3 仿真分析

本节通过仿真验证上述算法的有效性。以实际位置(8m，12m)为例，将萤火虫算法应用于磁信标定位时，首先确定目标函数，利用Matlab软件，建立标准磁场信息并利用萤火虫算法找到标准磁场的最大值，从而确定位置信息。

标准函数的图像如图3所示。

由图3可知，该函数的最大值有一个，但是峰值极高，在进行萤火虫算法时需要较多的迭代次数，可以得到一个较好的最大值。但是在实际应用中不能进行多次迭代，因为所需时间过长，不能实现实时的定位与跟踪，若仅仅是对静态目标进行定位则可以适当提高迭代次数。

所以为了准确确定目标所在位置，算法在主体进行萤火虫算法的同时，无需设置太多的迭代次数，在迭代次数较小时会有多个收敛结果，通过对这些收敛结果进行遍历验证，得到诸多最小值的点，找到收敛的点中效果最好的点。这样，函数的时间特性与准确性可以同时得到满足。

函数的等高图会出现尖峰，所以将函数的等高图放大，如图4所示。

由函数的等高线可见，该函数的最大值的尖峰很高，萤火虫算法的收敛结果将会有限，不会得到特别完美的运行结果。

函数的萤火虫算法迭代结果如图5所示。

通过图5可以看出，萤火虫算法最终收敛到几个点上，通过对上述100个萤火虫的横纵坐标进行优化，就可以得到正确的目标位置。这里选择函数图像中聚集最多的2个点，通过将这2个点代入目标函数值，找到这2个中较大的那个作为最优点，这样就可以输出正确的位置。

最终函数运行时间为5.6s，算法输出的位置信息是(7.82，11.80)m。取不同位置进行多次仿真，并将结果汇总如表1所示。

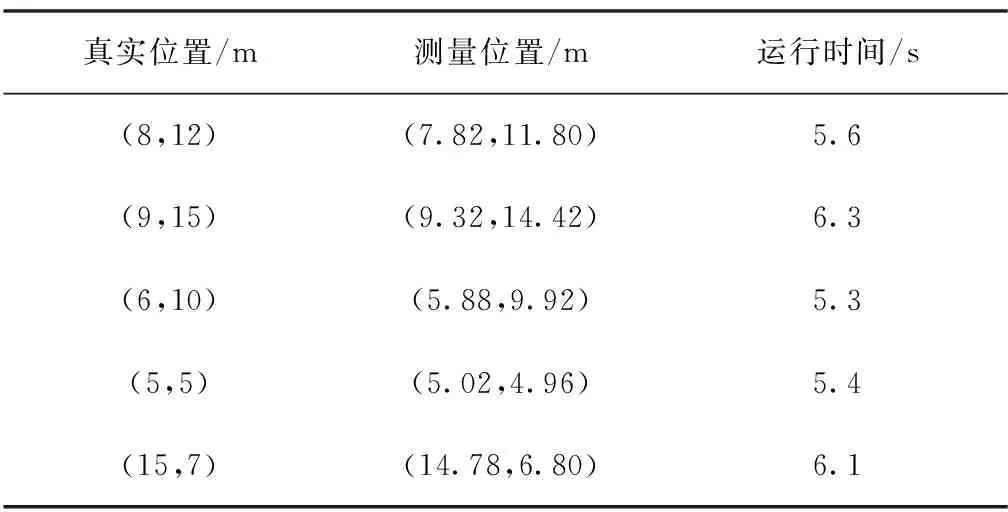
表1 萤火虫定位算法仿真结果

4 结论

1)研究了基于萤火虫算法的低频磁信标定位算法。

2)给出了磁信标定位的原理。

3)介绍了萤火虫算法的仿生学原理及其数学模型的建立过程与物理意义。

4)对于萤火虫算法中3个主要参数：光吸收系数γ、最大吸引力因子β0和随机项系数α的选取原则以及其如何影响算法性能进行了分析研究。

5)通过数学仿真验证了提出算法的有效性。