小波滤波在光纤惯导抗干扰初始对准中的应用

石利利，张志鑫，吴海仙，吉云飞

（北京航天时代光电科技有限公司，北京100094）

0 引言

初始对准是捷联惯导系统的关键技术之一，初始对准的精度和时间很大程度上决定着武器系统的性能和战斗力。在工程应用中，由于外界干扰因素的存在，惯导系统不可避免地存在角运动和线运动的干扰，从而难以实现快速对准。文献［1］详细推导了基于惯性系的粗对准算法来隔离晃动基座的影响，提高了晃动基座条件下的粗对准精度。但是，该方法只能有效隔离角运动干扰的影响，当线运动干扰较大时，对准结果收敛过程仍振荡剧烈，对准时间长，对准精度低。为解决此问题，可在对准之前进行预滤波，以减小高频噪声对对准性能的影响。

一般情况下，由于噪声主要分布在高频部分，通过合理设置截止频率，采用低通滤波器即可达到消除高频噪声的目的。但是，当有用信号和噪声相互混叠时，低通滤波效果不太理想。而小波滤波具有良好的时频特性和多尺度分析特性，能够分离出与噪声相混叠的有用信息。部分文献研究了小波滤波在初始对准中的应用。文献［2］证明了小波滤波可以提高光纤惯导精对准的精度，但对准时间较长。文献［3］、文献［4］讨论了在基于惯性系粗对准之前先进行小波预滤波对粗对准精度的影响，没有分析对精对准的影响，且以上文献都不满足实时性的要求。基于文献［5］、文献［6］提出的实时小波滤波方法，结合惯性系粗对准和Kalman滤波，本文通过车载实验重点研究小波实时去噪对对准精度和收敛时间的影响。

1 系统实现

传统的基于惯性系的双矢量定姿算法可以有效隔离角运动干扰，但是对线运动干扰敏感［7］，当线运动干扰较大时，若采用如图1所示的传统初始对准算法，光纤捷联惯导系统的对准性能仍较差。而本文先通过小波实时滤波算法对惯性仪表输出数据进行预处理，以减小高频噪声对对准性能的影响，然后进行惯性系粗对准和Kalman滤波精对准，系统实现流程如图2所示。

2 多尺度分析方法——Mallat算法

小波多尺度分析在时域、频域都有良好的局部化性质，具有 “数学显微镜”之称。利用小波的多分辨率特性对信号进行处理，尺度较大时，频率分辨率高，适于分析低频信号；尺度较小时，时间分辨率高，适于分析高频信号［8］，相当于多个带宽不同的滤波器对信号进行处理，滤波效果通常优于传统滤波器，近年来在音频、图像、探地雷达和医学成像与诊断等领域的信号处理中得以应用［9］。应用于小波多尺度分析的常见算法为Mallat塔式分解与重构算法［10］。以2阶样条小波函数ψ（x）为例，算法分为分解和重构两个过程，如图3所示。

设其分解的低通和高通离散滤波器分别为H和G，重构的低通和高通离散滤波器分别为h和g（h、g分别是H、G的对偶算子）。其中，C0为原始数据，C′0为经小波滤波处理后的数据；Ci（i＝1， 2，…，n）为低频系数，表征了信号的概貌信息；Di（i＝1，2，…，n）为各尺度高频系数，表征了信号的细节信息；“↓2” 代表2取1的 “抽取计算”，“↑2”代表在两个数据之间的 “插零运算”。重构过程中，各高频系数需先进行阈值处理，Ti（i＝1，2，…，n）表示各级的阈值大小。

3 小波实时滤波方案设计

小波域阈值滤波由Donoho于1995年首次提出［11］，由3个步骤组成：信号分解、信号去噪和信号重构。为达到理想的去噪效果，需要选择合适的小波基、分解尺度、阈值函数和阈值。

通常小波阈值降噪都是离线处理，无法满足惯组实时解算的需求。本文采用带滑动数据窗的小波滤波算法，并采用边界值重复的对称周边延拓的方法来处理边界问题，能够对惯性仪表输出信号实时降噪。具体实现方式如图4所示。

设数据窗的宽度为N，先输出与数据窗等宽的数据量x1～xN。当输出信号的长度达到窗口宽度时，开始动态获取N个输入值按顺序组成一维数组，并向右进行对称周期延拓，然后进行Mallat多尺度分解与重构，最终生成N个新数据x′1～x′N。其中，把x′N作为当前时刻T的滤波输出，下一时刻T＋1，采样得到新的原始数据xN＋1，此时先去掉x′1， 并将x′2～x′N依次向左移一个位置， 并将xN＋1补充到x′N空出的位置，组成新的一维数组。然后再对其进行对称周边延拓并进行小波滤波，循环执行以上操作，便可以实现对惯性仪表输出信号的实时降噪。

常用的阈值方法分为硬阈值法和软阈值法，本文采用软阈值法进行降噪处理，软阈值法表示为：

式中，wj，k为第j层小波系数，Tj为第j层小波阈值，小波阈值根据VisuShink阈值选取准则来确定，计算公式为：

式中，σj为各层噪声信号标准差，N为信号长度。在实际应用中，陀螺仪和加速度计噪声信号的标准差是未知的，所以在降噪前需要对噪声水平进行估计。噪声的标准差可以根据各尺度细节小波系数绝对值的中值来估计［12］，即：

另外，在实际应用中，需要根据信号特性以及合适的准则来选取小波基和分解尺度。设计实验（具体方法见第4节）得到惯性仪表在晃动基座下的输出信号，天向陀螺输出信号的频谱图如图5（a）所示。从频谱图中可以看出，信号中混入的噪声存在于全频段，发动机振动的频率主要集中在27Hz附近，在20Hz和53Hz附近有少量分布，走动、晃动的频率主要集中在1.8Hz和4.3Hz附近。不同方向的陀螺频谱图略有不同，但基本吻合。进一步分析各轴加速度计信号的频谱图，分析结果与陀螺频谱图基本一致。信号采样频率为f＝200Hz，采样频率和分解尺度共同决定了对应小波系数频带的范围，根据频谱分析结果，本文选取小波分解尺度为7层， 将频带限制到 0.8Hz（f/2/27）。 一般情况下，选择小波基时希望选择紧支撑、对称、正交性好以及消失矩高的母函数，通过比较几种小波的滤波效果，本文选取dB5小波作为小波基。

4 系统对准实验及分析

为验证预滤波效果，用光纤惯导系统在车载怠速条件下进行试验。试验总共进行了6次，每次采样时间为5min，将实测数据在Matlab中模拟实时降噪过程，利用前文所述的降噪方案对其进行预处理，窗口宽度为64。图5（b）给出了经小波滤波后天向陀螺输出信号频谱图，图6给出了预滤波前后天向陀螺输出信号的时域图。可以看出，除去刚开始小于窗口宽度的输出值，信号中的高频噪声得到有效抑制。

4.1 惯性仪表输出信号统计特性

比较了晃动基座下6组试验数据小波预滤波前后惯性仪表输出信号的统计特性，其中一组数据的比较结果如表1～表4所示。

表1和表3对比了预滤波前后陀螺仪和加速度计的均值，可以看出均值几乎不变；表2和表4对比了预滤波前后陀螺仪和加速度计的标准差，从结果中可以看出，经小波预滤波后光纤陀螺仪的输出噪声降到了滤波前的10%以下，加速度计的输出噪声降到了滤波前的5%以下。

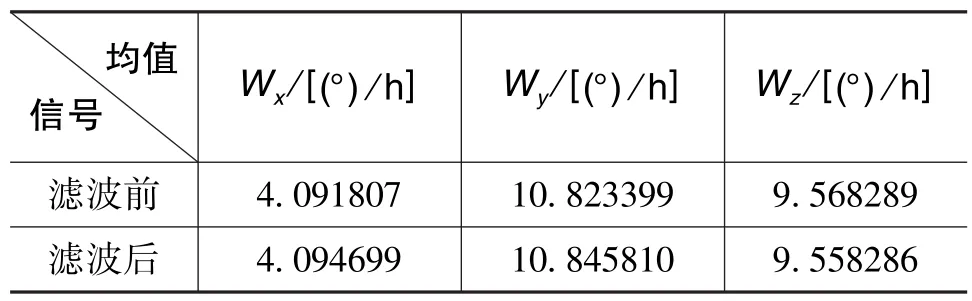
表1 小波预滤波前后陀螺均值Table 1 Mean value of gyro before and after wavelet pre⁃filtering

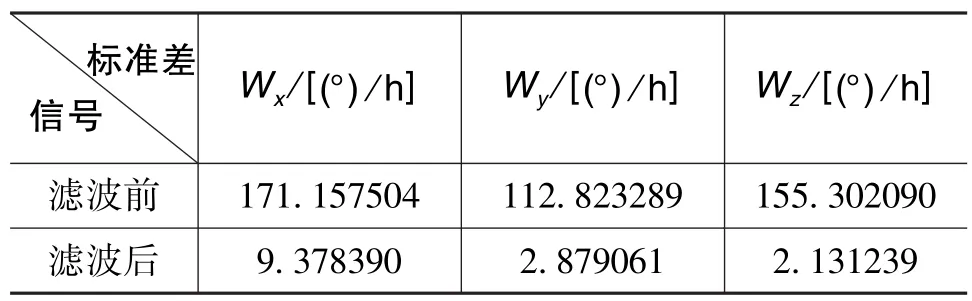
表2 小波预滤波前后陀螺标准差Table 2 Standard deviation of gyro before and after wavelet pre⁃filtering

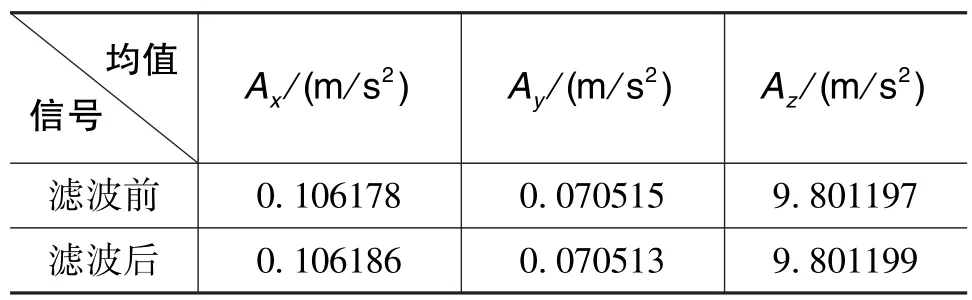
表3 小波预滤波前后加速度计均值Table 3 Mean value of Accelerometer before and after wavelet pre⁃filtering

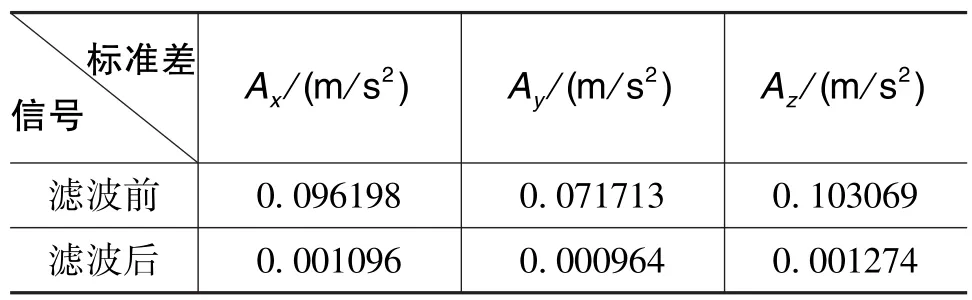
表4 小波预滤波前后加速度计标准差Table 4 Standard deviation of Accelerometer before and after wavelet pre⁃filtering

4.2 对准结果

传统初始对准算法和基于小波预滤波的初始对准算法，Kalman滤波的初始值P、Q、R取值不变，小波预滤波前后对准姿态角随时间的变化曲线如图7所示，表5为预滤波前后6次对准结果和标准差。

从图7可以看出，经过小波预滤波处理后，姿态角的收敛速度明显加快。滤波前精对准时间在100s以上，滤波后航向角在精对准50s即可达到较高精度，且收敛过程平稳性更高。表5给出了预滤波前后6次对准的结果，预滤波前，仅基于惯性系粗对准和Kalman滤波时，航向角的均方差为6.08′；预滤波后，航向角的均方差为2.77′。

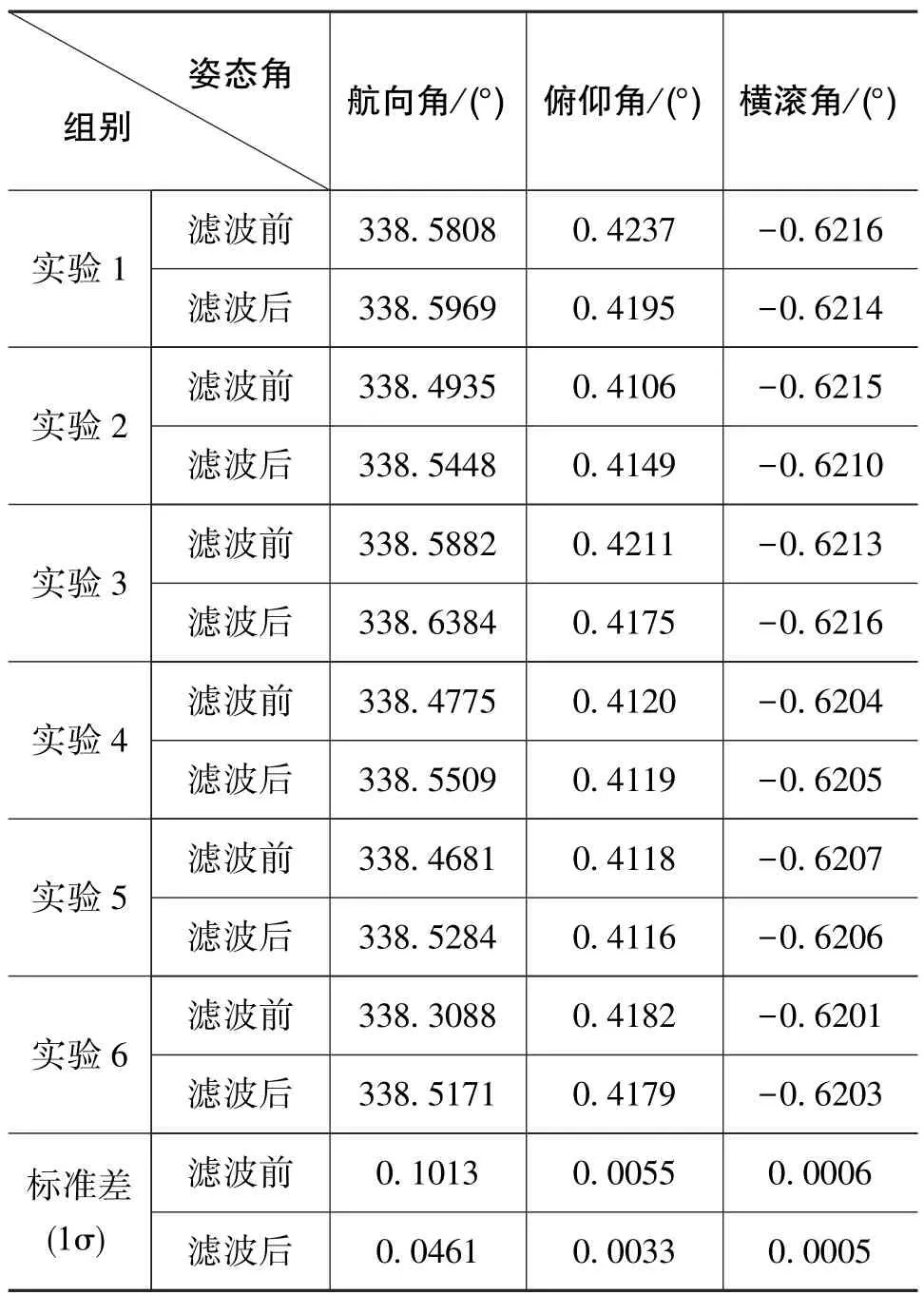
表5 预滤波前后6次对准结果和标准差Table 5 Six alignment results and standard deviation before and after pre⁃filtering

5 结论

晃动基座带来的角运动和线运动的干扰是影响惯导系统初始对准的重要误差源，本文综合考虑对光纤陀螺仪和加速度计的滤波效果和滤波的实时性，针对实测光纤捷联惯导系统的输出信号，设计出一种小波实时预滤波算法，并进行了基于惯性系的粗对准和Kalman滤波精对准的半实物仿真实验。实验结果表明，该方法既能满足实时性的要求，又能有效抑制光纤陀螺和加速度计的高频噪声。滤波前后，陀螺仪和加速度计的均值几乎不变，而陀螺仪的输出噪声降到了滤波前的10%以下，加速度计的输出噪声降到了滤波前的5%以下，能够实现晃动基座下的快速、精确自对准，具有一定的工程应用价值。