基于Reddy简化高阶剪切理论的复合材料对称角铺设矩形板横向弯曲一般解析解

张承宗

（空军军事代表局，北京100071）

0 引言

随着复合材料制造技术与工艺的提高，复合材料结构已经开始作为主承力件在先进运载器结构中使用，如美国研制的轻型攻击直升机RAH－66机身龙骨大梁复合材料铺层最多已达1000层。可以预计，未来航空航天复合材料结构铺层可能更多、更厚。复合材料厚板具有较低的横向剪切刚度，在载荷作用下横向剪切变形比较明显，在很多情况下，采用剪切变形理论计算复合材料结构力学响应是必要的。考虑到复合材料结构还有各向异性等诸多问题［1］，考虑横向剪切效应的复合材料结构板壳力学研究在理论和工程领域日益凸显其重要性。实际工程中大多采用有限元程序进行结构力学计算，然后根据力学强度试验或者用力学解析解校核，再针对不同情况进行分析计算。显然，力学解析解校核有限元法计算精度是一种经济的做法，解析解还可以在力学机理研究中有着独特的作用。尽管复合材料结构数值解法蓬勃发展，解析解研究依然是复合材料力学的重要研究内容。随着力学模型日趋复杂，力学解析解的建立变得困难起来，相应地新的力学解析解法和理论也不断地发展。

对于各向同性和正交铺设、反对称铺设层合板 壳 ， 传统 Levy级 数 方 法［2－3］、 双 重 级 数 方 法［4］在有些情况下依然可用。钟万勰［5］从哈密顿体系角度提出了求解偏微分方程和力学方程的新思路，取得一些解析解，姚伟岸等［6］开启了辛弹性力学思路。胡文锋等［7］采用状态空间法获得了正交异性厚矩形板多种边界条件下的解析解，卿光辉等［8］得到了基于状态方程的矩形层合板多种边界条件下的解析解；张承宗等［9］研究了一种求解直角坐标系下4阶常系数线性偏微分方程定解问题的新方法：复级数展开法 （复数分离变量法），并用于求解各向异性板横向弯曲问题。这种复级数展开法推广用于基于经典理论和一阶剪切理论的复合材料圆形板、矩形板、斜形板等相关力学问 题 ， 取 得 一 些 解 析 解 和 结 果［10－12，15－16］， 黄 炎等［13］、 杨 端 生 等［14，17］应 用 复 级 数 展 开 法 思 想 获得了各向异性矩形板振动、屈曲问题解析解。从目前研究来看，复级数方法 （复数分离变量法）或可以看作数学物理的一个基本方法［18－19］，可以用来求解常系数的线性偏微分方程 （组），而复合材料板壳结构力学控制方程大多属于此类偏微分方程 （组）。对于复合材料结构板壳理论，先后提出了经典理论和一阶剪切理论、高阶剪切理论和Reddy简化高阶剪切理论等。相比一阶剪切理论，Reddy［20－21］简化高阶剪切理论复杂程度提高不多，特别是不需要对剪切刚度进行修正，这种剪切理论有其自身优势，贺丹等［22］应用这种简化高阶剪切理论取得有益的结果。受到先前数学解析手段局限，基于Reddy简化高阶剪切理论的复合材料中厚板壳结构力学问题解析研究相对有限，结合各向异性、剪切变形综合解析研究的工作还没实质进行。本文运用复级数方法，采用Reddy简化高阶剪切理论针对复合材料对称角铺设 （各向异性）矩形层合板横向弯曲进行解析研究，首次获得了基于Reddy简化高阶剪切理论的复合材料对称角铺设 （各向异性）矩形层合板横向弯曲一般解析解，进行了计算验证，并与经典理论、一阶剪切理论解析解进行对比计算。文中给出的解析计算结果，可用于校核有限元等工程计算软件。

1 基本理论

根据文献［20－21］，基于Reddy简化高阶剪切理论的复合材料对称角铺设 （各向异性）层合板在弯曲变形分析时的位移分量为

式中，w（x，y）为挠度，фx（x，y）和фy（x，y）分别为板广义位移参量。

定义下列广义刚度

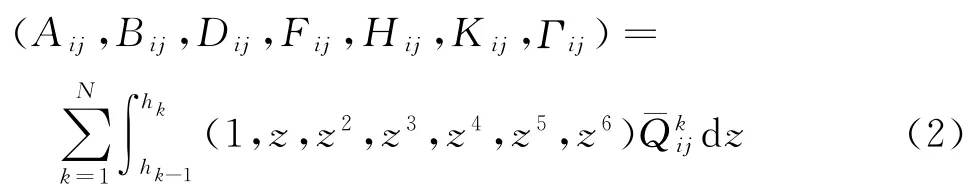
引入以下无量纲量：

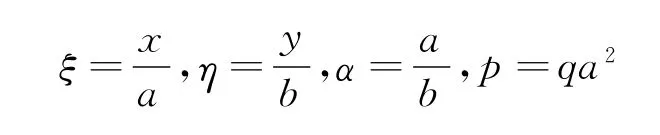
其中a、b、h为矩形板的长、宽、厚，q为横向载荷。

该复合材料对称角铺设 （各向异性）层合板横向弯曲问题的力学平衡方程可写如下形式：

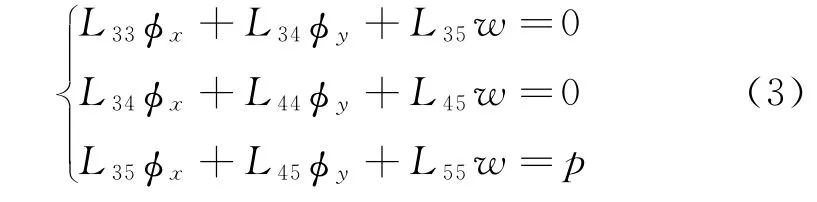
其中

基于Reddy简化高阶剪切理论的各向异性（复合材料对称角铺设）横向弯曲问题求解在数学上可归结为求解偏微分方程组 （3）在横向弯曲矩形板边界条件下边值问题。

2 一般解析解的建立

本文采用位移法［12］求解基于Reddy简化高阶剪切理论的各向异性板 （复合材料对称角铺设）横向弯曲问题。

2．1 通解的推导

设

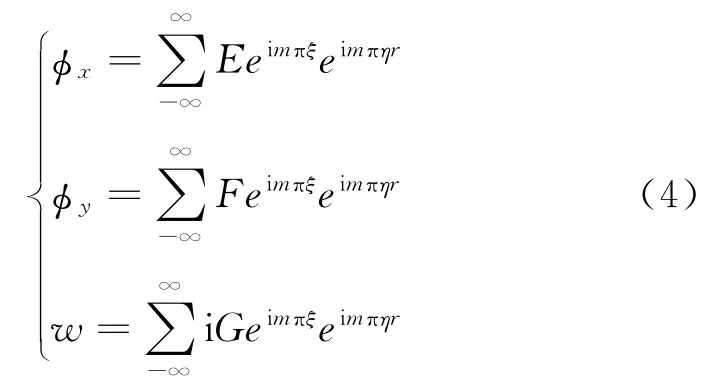
式 （4）中i为虚数单位，m 为整数 （m ≠0），r为特征根。E、F、G为复数常数。

将式 （4）代入式 （3），当m 不为0时，可推得有关r的8次特征代数方程

式 （8）中，S8，…，S0为复数常数，可以采用MATHCAD软件推导获得，形式复杂 （略）。对于各向异性材料矩形板，式 （5）有4对共轭复根ak±bki（k＝1，2，3，4）。

按照［12］类似步骤，可以推得实数形式级数通解фx、фy、w

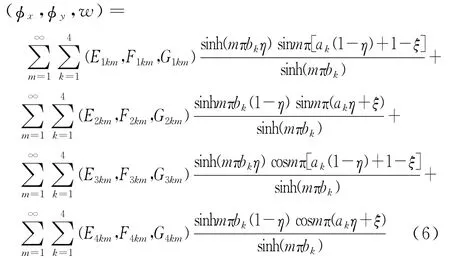
将式 （6）代入式 （3）任两式，从基本解sinh（mπbkη）sinmπ（akη＋ξ）、sinh（mπbkη）cosmπ（akη＋ξ）、cosh（mπbkη）sinmπ（akη＋ξ）和cosh（mπbkη）cosmπ（akη＋ξ）的独立性出发，可得到Ejkm、Fjkm、Gjkm（j，k＝1，2，3，4）之间的关系矩阵

式 （7）中Zmnk、Rmnk（m，n＝1，2，3，4）为实数常数。

当m为0时，设

其中，фxy、фyy，wy为待定实数常数。将式 （8）代入式 （3）可得另一个关于r的4次代数特征方程和4个特征根：±a0，1、±a0，2。根据常微分方程理论，可求得另一组关于η的双曲正弦函数形式和多项式形式补充解。

考虑一般性，又设

式 （9）中i为虚数单位，n为整数（n≠0），s为特征根，O、P、Q为复数常数。

类似地，可得有关s的特征方程 （10）及其4对不等共轭虚根ck±dki （k＝1，2，3，4）和关系矩阵：

其中，式 （10）中T8，…，T0为复数常数，形式略。式 （11）中Tmnk，Smnk（m，n＝1，2，3，4）为实数常数。同样可得对应的实数形式级数通解

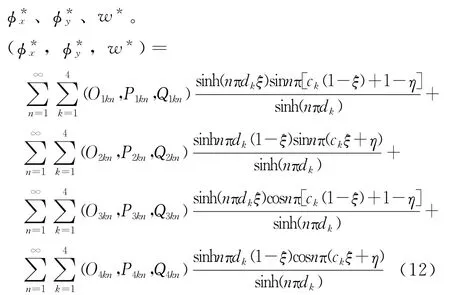
同样，当n为0时，设

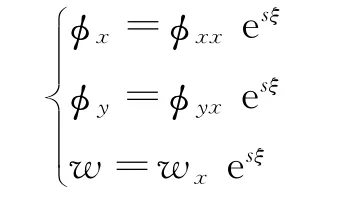
其中，фxx、фyx、wx为待定实数常数。将上式代入式 （3）可得另一个关于s的4次代数特征方程及特征根：±c0，1、±c0，2。 根据常微分方程理论，可求得另一组关于ξ的双曲正弦函数形式和多项式形式补充解。

从线性偏微分方程解的可迭加性出发，在式（6）和式 （12）基础上补充两个坐标方向的梁函数形式解、关于ξ和η的交叉多项式及特解，可得如下一般解析解：

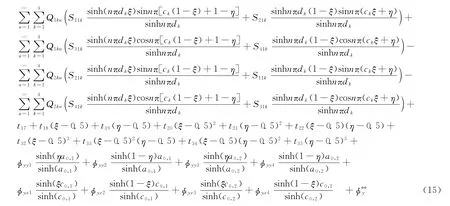
2．2 特解的建立

对于横向弯曲问题，本文引入势函数Φ，引进微分算子Χ0，它是以式 （3）中算子Lij组成得3×3行列式值。依照线性代数理论，基本微分方程 （3）可以写成

其中，方程系数可采用MATHCAD软件推导获得，具体形式略。

令Χkl（k，l＝1，2，3）表示给该行列式的代数余子式。使

对于均布载荷q，本文选取

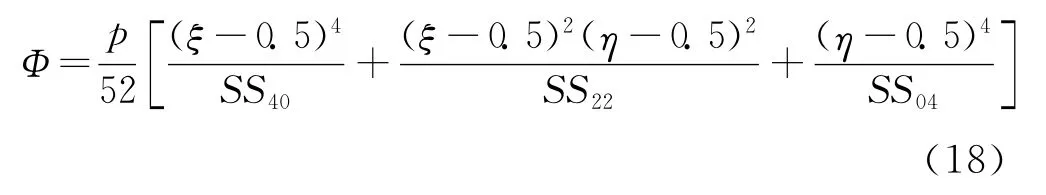
其中，SS40、SS22、SS04分别为算子Χ0中关于的系数。式 （15） 中特解

2．3 求解模式

将式 （13）～式 （15）的多项式部分 （对应

结合式 （16）和式 （18），可以推出式 （13）～于tk（k＝1，2，…，35）的各项）代入式 （3）的三式可得23个独立方程，这样多项式形式补充解只有12个未知数是独立的；将式 （13）～式 （15）中的双曲正弦函数形式解代入式 （3）中任两式，根据双曲正弦 （余弦）函数的独立性，可将фxy1、фxy2、фyy1、фyy2用Wy1、Wy2表示，可将фxy3、фxy4、фyy3、фyy4用 Wy3、Wy4表 示， 将 фxx1、фxx2、фyx1、фyx2用 Wx1、Wx2表示， 将фxx3、фxx4、фyx3、фyx4用Wx3、Wx4表示，这样双曲正弦函数形式解只有8个独立未知数（Wx1、Wx2、Wx3、Wx4、Wy1、Wy2、Wy3、Wy4）。在实际计算中，m、n不可能取无穷大，设m、n最大取M，这样一般解析解式 （13）～式 （15）共有16 M＋20个未知数。对于采用Reddy简化高阶剪切理论的矩形板，每边有4个边界条件，共有16个边界条件。将一般解析解代入16个边界条件中，形成16个方程，将所得每个方程展成M 项正弦级数。根据正弦级数的正交性，可以得到16 M 个线性代数方程。矩形板每个角点处可有位移 （如挠度、转角）或内力 （如弯矩、剪力）等5个角点条件，共有20个角点条件，这样共建立16 M＋20个方程，可以求解16 M＋20个未知数，该横向弯曲问题得解。

3 数值算例验证

下面计算对称角铺设四边固支矩形板在均布载荷q作用下的横向弯曲，以验证解析解。板结构参数为a＝b＝1m，载荷参数为q＝104N／m2，材料力学参数为：E1＝276GPa，E2＝31．05GPa，G12＝G13＝10．35GPa，G23＝12．42GPa，ν12＝ν13＝0．25，ν23＝0．28。

四边固支矩形板 （CCCC）边界条件为：

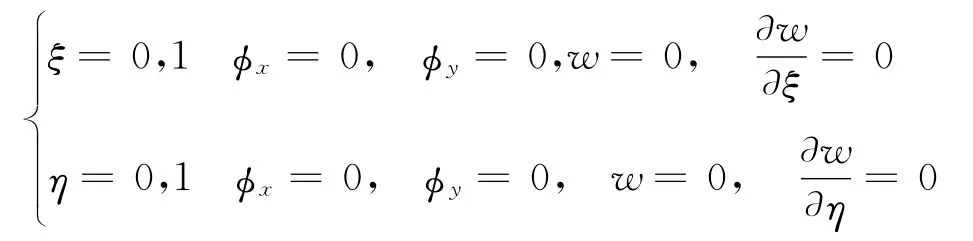
该弯曲问题中挠度中心对称；фx、фy反中心对称，据此可降低计算量。

3．1 稳定性验证

对于级数解来说，其稳定性验证是必需的。为了考查本文解的收敛性和稳定性，针对11层［30°／－30°／30°／－30°／30°／－30°／30°／－30°／30°／－30°／30°］四边固支正方形板 （h＝0．1m），对在均布载荷作用下的横向弯曲进行计算，改变M 比较相应板中心挠度。挠度单位为m，弯矩单位为N·m。

表1 M 对板中心挠度、弯矩计算值影响Tab．1 The effect of Mon the numerical results ofω （0．5，0．5）and Mx （0．5，0．5）

表1表明当M 增大时，解数值保持稳定；计算中发现，对于不同的材料、边界条件及铺层方式 ，所需计算项数可逐渐增大M 试算以确定具体数值。

3．2 边界条件符合程度验证

为检查本文解对边界条件符合情况，针对单层铺设角为30°的正方形板 （h＝0．1m）进行计算 （M＝60）。板挠度w、广义位移фx和фy见表2～表4。

表3 ［30°］CCCC层合板фx分布Tab．3 The distribution ofфx （x，y）over the CCCC laminated plate with［30°］ply

表4 ［30°］TCCCC层合板фy 分布Tab．4 The distribution ofфy （x，y）over the CCCC laminated plate with［30°］ply

从表2～表4可发现本文解对边界条件符合程度较好。

对于复合材料板结构，当其厚度很小时，板横向剪切变形亦很小，应该可按经典理论计算分析板结构，此时按剪切变形理论计算结果应与经典理论结果相当。为此，固定a＝b＝1m，改变h，结合不同a／h， 针对具有CCCC边界条件［45°／－45°／45°］层合方板 计算 中心挠度和弯矩值，并将Reddy简化理论解与经典理论CLT［9］、修正剪切刚度的一阶剪切理论 （first－order deformation theory，FSDT）［12］进 行 对 比 （M 取40）。结果见表5～表6。

表5 ［45°／－45°／45°］CCCC层合板中心挠度Reddy解与CLT、FSDT解比较Tab．5 Comparisons ofω （0．5，0．5）in the CCCC laminated plate with［45°／－45°／45°］ply and different a／h using simplified high order shear deformation theory with those of CLT and firstorder deformation theory

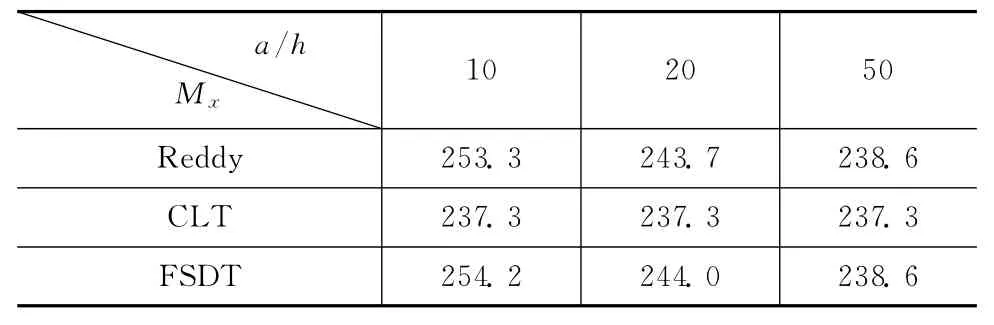
表6 ［45°／－45°／45°］TCCCC层合板中心弯矩Mx （0．5，0．5）Reddy解与CLT、FSDT解比较Tab．6 Comparisons of Mx （0．5，0．5）in the CCCC laminated plate with［45°／－45°／45°］ply and different a／h using simplified high order shear deformation theory with those of CLT and firstorder deformation theory

从表5～表6可看出，当a／h增大到一定值时，Reddy解与CLT、FSDT解挠度值已相差不大；当a／h降低到一定值时，Reddy解与CLT解挠度值、弯矩逐渐出现差距，经典理论给出偏低的挠度值和偏低的弯矩值，偏于危险结论。在目前设定的边界条件、铺设方式、结构尺寸下，Reddy解与FSDT解挠度值、弯矩比较接近，FSDT解挠度值一般要大于Reddy解挠度值，文献［23］给出的算例表明FSDT解挠度值要大于三维状态空间解挠度值，这表明本文Reddy解挠度值和文献［23］结论趋势相符，也从另一个方面验证了本文解的正确性。

4 结论

综合考虑复合材料结构各向异性和横向剪切效应更符合复合材料板壳的实际力学状态，另一方面增加了复合材料结构力学问题解析求解的难度。解析求解经典理论各向异性板弯曲涉及求解一个挠度函数的4阶偏微分程边值问题，求解一阶剪切理论的各向异性板，则涉及求解3个位移函数的6阶偏微分方程组边值问题。Reddy高阶简化理论不需要对剪切刚度进行修正，可望获得更加准确的力学响应结果，但解析求解基于Reddy高阶简化理论的各向异性矩形板弯曲问题要求解3个位移函数的8阶偏微分方程组边值问题，数学求解更加复杂，解析求解一直也没有实现。本文依据复数级数方法首次获得了基于Reddy简化高阶剪切理论的复合材料对称角铺设 （各向异性）矩形层合板横向弯曲一般解析解，数值计算验证了所得解析解的收敛性、稳定性。本文解析解的建立为采用Reddy简化高阶剪切理论解析研究复合材料板结构力学影响打下了基础，后续将据此开展有关计算研究。