能量有限元方法的双星整流罩中频声振环境预示

王怀志，于开平，曾耀祥，王旭，张宗强

（1．哈尔滨工业大学航天学院，哈尔滨150001；2．北京宇航系统工程研究所，北京100076；3．西安航天动力测控技术研究所，西安710025）

0 引言

飞行器在飞行过程中要受到各种复杂载荷作用，对于整流罩结构来说，外部噪声 （尤其是中高频噪声）对结构及内部有效载荷的影响很大，如何对这种中高频噪声作用下的结构进行振动环境预示是一个很重要的研究方向。

对于目前的振动环境预示来说，常用的有基于单元类的有限元 （FEM）和边界元 （BEM）方法，基于能量意义的统计能量方法 （SEA）以及混合类方法。而能量有限元方法 （EFEA）是近些年来出现的一种基于能量的，主要用于中高频振动环境预示的方法，它集合了单元类方法和能量类方法的优点，能够较好解决单元类方法在高频域带来的计算量问题，同时对结构的不确定性问题不敏感，相对于传统的能量类方法又能够考虑能量在结构上的分布。

EFEA属于功率流类方法［1］，Nefske等［2］最早基于波动理论建立了简单梁结构的能量密度控制方程。此后，能量有限元的研究经过较多的发展，目前在工程上已经有一定的应用，Zhang等［3］将能量有限元方法应用于某潜艇结构，Vlahopoulos等［4］对复合材料舱体结构进行了能量有限元分析，并与实验结果进行了比较，获得了较好的结果。在国内，孙丽萍等［5］将能量有限元方法应用于某简化护卫舰的机座结构，徐福慧［6］采用能量有限元方法对某齿轮箱结构的振动特性进行了研究，林毅［7］对某导弹舱体结构进行了研究。EFEA还有其他的一些应用，包括游进等［8］对耦合板结构进行了研究，陈书明等［9］对声腔和板耦合系统进行了研究，并与SEA和实测值进行了比较。

对于卫星整流罩结构，目前主要的研究采用统计能量分析方法，如孙目等［10］采用SEA方法对某整流罩结构进行了噪声环境预示，王昆［11］采用SEA方法研究了整流罩结构的声振特性，宋海洋等［12］采用SEA方法对火箭整流罩的减振降噪问题进行了研究。此外，赵小见等［13］采用有限元方法对整流罩结构在噪声下的腔内噪声分布进行了研究，但是其结果只在低频内有效，朱卫红等［14］采用混合法 （FE－SEA）对整流罩－卫星－仪器舱－适配器的组合体进行了预示，通过与实验数据比较验证了预示方法和结果的有效性。

综上所述，目前能量有限元方法在解决复杂问题，尤其是在航天领域的一些复杂结构的应用极少，且现有的应用都是将复杂结构简化为很简单少数板梁结构耦合系统，难以对更为复杂的结构如卫星整流罩结构进行预示。而传统采用的有限元方法无法解决中高频的预示问题，SEA方法只能给出子结构的平均响应信息，即使是混合方法 （如FE－SEA），对于声腔内部以及部分关注部位的响应也无法给出。

鉴于此，本文基于能量有限元方法，建立了双星整流罩的EFEA模型，并借助于NASTRAN的EFEA模块，对该复杂结构的动力学环境预示，并得到了符合预期的预示结果。

1 板的能量有限元理论

在稳态下，对于图1所示的单元体，其能量流平衡方程［13］为式 （1）。

图1 单元体的能量流Fig．1 The energy flow of the unit element

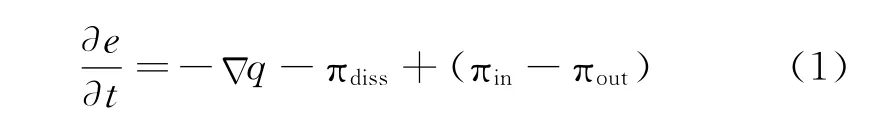
在式 （1）中，e表示结构的能量密度，q表示功率流 （单位时间内流经单位边界尺寸上的能量），πdiss＝ηω〈珋e〉表示结构损耗的能量，πin表示结构的输入能量，πout表示结构传递给其他系统的能量，（πin－πout）表示单元体的净输入能量，对于没有能量交互的单系统来说，净输入能量为πin，后文的公式推导主要对单系统来进行。

根据 Nefske等［2］的假设以及对梁［14］和板［15］的能量流关系的推导可知，能量密度与能量流的关系类似于热传导的关系，即

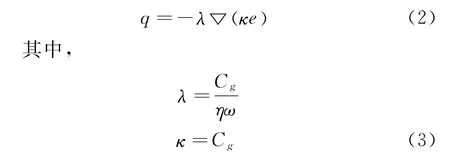
式 （3）中，η为结构的内损耗因子，Cg为结构的群速度，考虑稳态情况时这样可以得到板的能量密度平衡方程。

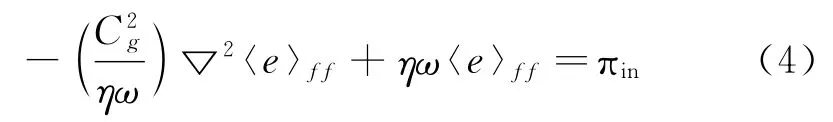
其中，〈e〉ff表示对能量密度进行空间和单个频率周期内做平均，根据Galerkin加权余量方法，可以得到能量有限元方法的方程。

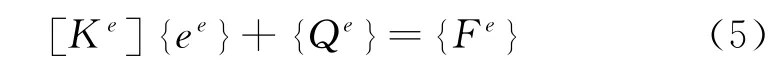
假设权函数为Nii＝1，2，…，m（

），

其中，［JCe］的表达式为［3］：

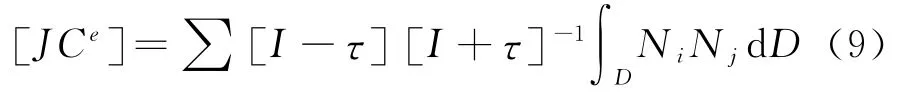
结构和声的能量密度与其均方根速度值满足以下关系：

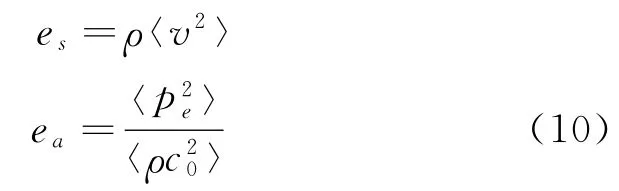
式 （10）中，es表示梁板结构的能量密度，〈v2〉表示对应结构的速度的均方值，ea表示声腔的能量密度，pe表示声压的有效值，〈p2e〉表示声压有效值的均方值，c0表示当前状态下的声速。

根据统计能量分析中关于统计平均的理论［17］，速度与位移和加速度的均方值具有以下关系：

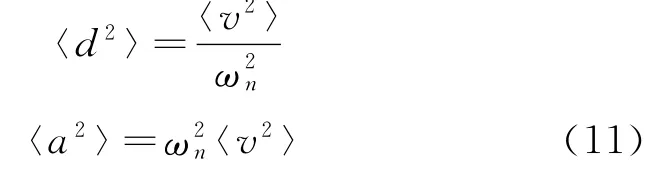
〈d2〉、〈v2〉和〈a2〉分别表示频带内位移、速度和加速度的均方值，ωn表示频带中心频率对应的角频率。根据式 （10）和式 （11）可以通过能量密度得到带宽内位移、速度和加速度的均方值。

对于能量有限元方法的上限频率，可以由式（12）给出［18］：

其中，l为结构的特征长度。

2 NASTRAN中EFEA模块的应用

MSC．NASTRAN的EFEA模块是目前可以使用的商用能量有限元方法模块，主要用来解决中高频域的复杂结构的振动、声振耦合等问题。该模块可以建立杆、梁、板、噪声单元以及相互之间的耦合，可以对复合材料、加筋结构进行建模，可以模拟结构吸声、焊点、接缝以及湍流边界等复杂特性。

利用MSC．NASTRAN进行EFEA分析主要包括5个步骤 （如图2所示）：前处理 （建立有限元模型）、EFEA预处理、能量有限元建模、EFEA分析以及后处理。

图2 MSC．NASTRAN进行EFEA分析流程Fig．2 MSC．NASTRAN EFEA analysis flow chart

建立有限元模型需要借助MSC．PATRAN或者Hypermesh等有限元建模软件，有限元模型建立以后，对于输出的bdf文件采用pre－efea模块进行前处理，可以得到处理后的文本格式的模型文件，在该模型文件的基础上进行EFEA建模，需要对结构的载荷、分析频带、材料、阻尼损耗因子等参数进行建模，并添加出控制等信息［19－20］，已经完成的EFEA模型文件如图3所示。

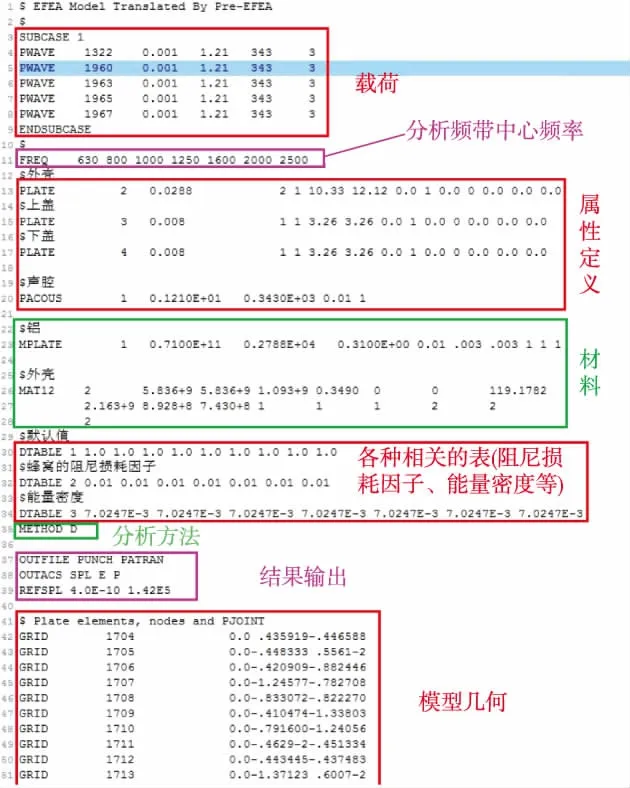
图3 进行EFEA分析的模型文件结构Fig．3 The structure of the EFEA model file

图3中给出了进行能量有限元分析的文本格式模型文件，模型需要定义载荷、分析频带、材料属性、损耗因子以及输出等几个部分，这与VAOne对SEA的建模具有很大的相似性。各种属性采用NASTRAN的卡片［21－22］来指定，卡片参数的定义与SEA中的参数定义保持一致。

分析结果可以输出结构能量密度、均方根速度等，声腔的能量密度、声压的均方根以及声压级，结果文件可以直接输出文本、PUNCH文件、Matlab直接识别的MAT文件以及可以导入PATRAN进行后处理的文件 （输出类型选PATRAN）。

3 在整流罩结构中的应用

本文采用能量有限元方法对某双星整流罩结构进行了振动环境的预示，该结构示意图如图4所示。

图4中标注了双星整流罩的主要结构，各舱段之间的连接段有加强框 （图4中未标注），上星支架、上星过渡支架和上星将整流罩结构分成两段。根据上述简化结构对该双星整流罩进行有限元建模，得到结构的有限元模型如图5所示。

在建模的时候，壳体部分采用三角形单元，内部声腔采用了四面体单元，因为能量有限元模块要求壳体和声腔之间的单元节点耦合起来以方便在对应位置生成实体－壳之间的耦合连接，对于较复杂的结构划分成四面体单元和三角形单元较为容易。

考虑到在实验过程中，整流罩底部固定在基础上，下星支架、下星过渡支架和基础之间也构成一个小的声腔，所以该模型建模时实际上包含3个声腔。根据实际情况，需要对3个声腔进行建模。声腔的声压级是工程上非常关注的事项，也是本文动力学环境预示的一个主要内容。

在整流罩结构中，外部所有的壳体、上下卫星支架以及上下卫星过渡支架为蜂窝夹心结构，对该结构的建模采用三明治夹心理论进行了简化，采用EFEA模块的夹层板单元属性进行建模。尾部倒锥部分为加筋板结构，采用EFEA的加筋板属性进行了相关的建模工作。

该整流罩结构置于外部声场中，通过对结构的能量传输关系进行分析，得到能量流传递路径，如图6所示。

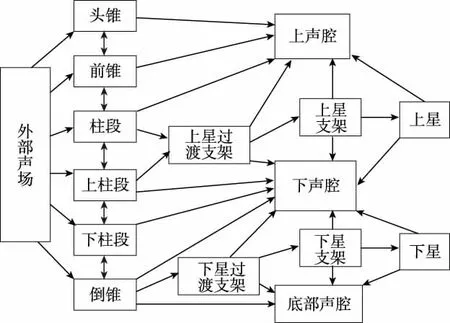
图6 能量流传递路径Fig．6 The schematic diagram of the energy flow between subsystems

在能量传递的过程中，子系统本身还具有能量的损耗，即结构的内损耗因子和耦合损耗因子部分。

然后分析整流罩结构的能量传输路径，从图6可以看出，能量主要通过外部壳体以及上下星支架和过渡支架部分传递到内部声腔，结构部分相互连接之间存在能量的交换，根据图6的能量传递关系，可以建立如图7所示的整流罩统计能量分析模型。

图7 双星整流罩SEA模型Fig．7 The SEA model of the fairing structure

根据该双星整流罩结构，考虑材料属性的差异，将该结构划分为70个统计能量子系统，其中有3个声腔子系统，7个半无限大声场，60个板壳子系统。半无限大声场与双星整流罩外部壳体部分连接，模拟外部壳体与外部声场之间的能量辐射，混响场激励采用VA One中的Diffuse Acoustic Filed进行建模。

4 整流罩结构的EFEA分析

整流罩外壳受到混响场声压激励，其声压级（Sound Pressure Level，SPL）曲线如图8所示。

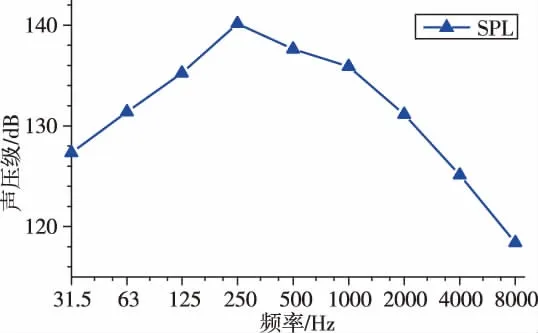
图8 整流罩声场的声压级曲线Fig．8 The SPL curve of the sound field

阻尼损耗因子一般情况下需要通过实验的方式测得，由于条件的限制，本文中的模型不能得到基于实验验证的阻尼损耗因子，文中结构的内损耗因子设置参考了文献 ［21］的公式。而耦合损耗因子则基于NASTRAN的EFEA模块和VA One分别自动计算得到。

对该整流罩结构进行EFEA分析，可以得到上下声腔的声压级响应结果，如图9～图12所示。

本文中的实测数据来源于对整流罩进行混响声场的实验。实验时，整流罩竖直置于混响场中心，底部由橡胶垫支撑，支撑垫的频率低于分析频率的下限。

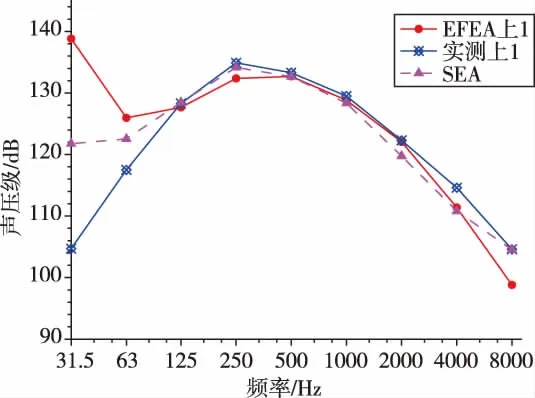
图9 上声腔上端声压级Fig．9 The SPL of the top of the upper cavity

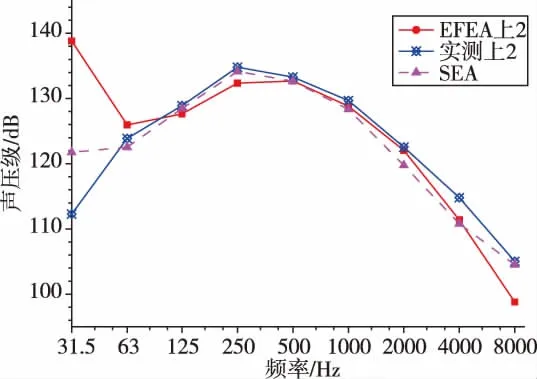
图10 上声腔下端声压级Fig．10 The SPL of the bottom of the upper cavity

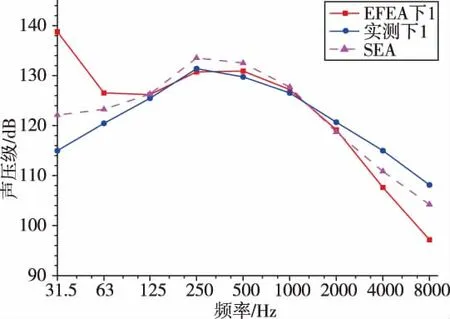
图11 下声腔上端声压级Fig．11 The SPL of the top of the lower cavity

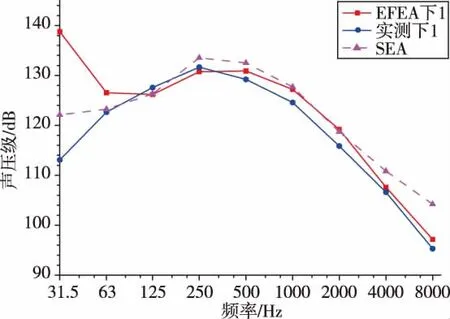
图12 下声腔下端声压级Fig．12 The SPL of the top of the lower cavity

比较可以发现，在频率较低时，采用SEA和EFEA预示结果与实测值相差较大，在125Hz～2000Hz的频段内，EFEA的预示结果与实测值相比误差基本小于3dB，大于2000Hz时误差开始增大。本文模型及其仿真结果得到的EFEA方法更适合中频段的动力学环境预示问题，这与EFEA方法的理论以及之前的理论验证结果是相符的。

与实验值的比较可以发现，在低频段两种方法都出现了较大的误差。这是由于在低频时，子系统的模态叠合数 （Modal Overlap）很小，而能量类方法采用了频带和空间上统计平均，其引入的误差会变得很大；在125Hz～2000Hz范围内，两种方法都得到了基本符合要求的预示结果，其中，能量有限元方法的结果与实测结果更为接近。

整流罩结构部分进行EFEA分析后，得到的1000Hz频段的均方根速度分布云图，如图13所示。

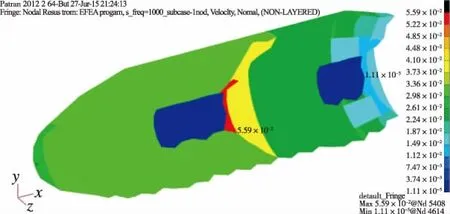
图13 用PATRAN显示的结构的速度均方根分布Fig．13 The RMS distribution of the structure by PATRAN

图13采用了半剖视图，显示了整体结构的均方根速度分布，通过云图可以得到关注结构速度值极值的位置，这是能量有限元方法相对统计能量分析方法的一个优势。

在本结构中，测点主要分布在头锥、前锥、柱段、上星支架、上星过渡支架、上柱段、下柱段、倒锥、下星支架、下星过渡支架等结构的上下部位。仿真值与实测值对比如表1所示。

在表1中，采用20×log10 （P／P实测值）计算得到均方根加速度以dB为单位的相对误差。从表中的数据对比可以发现，采用SEA和EFEA两种方法得到的结果在大部分位置上相比差别不大，与实测值相比，两种方法大部分测量位置的加速度响应基本满足工程要求，但EFEA方法能够得到更加精细的响应分布信息。此外，考虑到能量有限元方法在连接部分能量密度是不连续的，而统计能量分析方法是对子系统进行平均的结果，所以在连接部分实际上也是理论上产生较大误差的位置。综上考虑，采用EFEA对整流罩进行的振动环境预示基本符合预期。

表1 主要结构部分的均方根加速度值比较Tab．1 The RMS of the Acceleration of the main structure

此外，通过对3种尺度模型，采用SEA和EFEA方法进行了计算效率的比较，模型及计算耗时如表2所示。

表2 两种方法计算耗时比较 （单位：s）Tab．2 Computation time costs of SEA and EFEA （unit：s）

从理论上来说，计算的频带数和子系统数目决定了SEA方法的计算耗时，而EFEA方法则与计算频带数与模型的节点数／自由度数相关，EFEA方法的计算耗时大于SEA方法，这与理论预期是相符的。有限元方法的计算耗时取决于模型的自由度数，且有限元方法和EFEA方法进行求解使用的求解器是相同的，理论上来说自由度数相同时，两者的计算耗时应该是相近的，所以本文未单列出有限元的计算耗时。但是对于相同的模型，EFEA方法由于可以划分更为粗略的网格，因而理论上可以很大程度上减少有限元方法的计算量。

5 结论

本文采用EFEA方法，建立了某双星整流罩结构的能量有限元模型，同时建立了该结构的SEA模型，完成了该结构的振动环境的预示，通过对EFEA、SEA方法的预示结果与实验测试结果的比较可知，采用能量有限元方法可以较好地完成复杂工程结构在中间频段内的振动环境预示工作，且相对于SEA方法，EFEA可以得到预示结果的空间分布。在本文中，将EFEA方法运用到较为复杂的实际工程结构，并给出了采用NASTRAN中EFEA模块进行能量有限元建模的方法，可以为后续该方法的研究以及在航天工程中的进一步应用提供一定的借鉴。