基于核密度估计的水上交通事故黑点辨识研究*

2018-10-12王艳锋崔永孝

武汉交通职业学院学报 2018年3期

王艳锋崔永孝吕露

（1.武汉交通职业学院，湖北武汉 430065；2.长江三峡通航管理局，湖北宜昌 443000）

1 引言

我国海事部门多年以来统计了相关水域发生的各种水上交通事故，通过对这些事故数据的分析，可以看出，从空间的角度来讲，水上交通事故的发生，在地理位置上呈现出或离散或集中的状态［1］。通过查阅相关资料和事故调查报告、相关报道等可以看出，相对离散的事故，发生原因大多与人因相关，而相对集中的事故则复杂很多，其产生原因常与事故现场的通航环境有着千丝万缕的联系。

毛喆［2］等人运用DBSCAN算法对长江干线进行黑点段划分，分析辨识出的黑点段及其水上交通事故的特征和原因，与相应区域的实际通航环境相吻合，证明采用此分析研究长江干线的事故分布规律是可行的。杜珊珊［3］等人建立了基于凝聚型层次聚类算法的水上交通事故黑点辨识模型，以2006-2011年长江江苏段张家港辖区的水上交通事故统计数据为例，分析辨识结果，并结合实际通航环境分析黑点产生的原因，提出对策。梁璟［4］等人研究发现研究对象存在着许多问题，主要是数据缺失和信息错误，具体表现为样本母体数量小、事故调查报告信息不全、缺少事故发生详细地点或里程等信息的问题。通过模糊综合评判法和图上作业的结合，将黑点分析方法进行了定性定量的改进，实现黑点的辨识。

一定时间、一定区域内，水上交通系统受各种风险因素的影响，在空间分布上表征明显。分析水上交通事故黑点的空间分布特点，不仅对水上交通事故的致因理论有贡献，还有利于海事部门对水上交通安全的管控和治理工作。

2 核密度估计方法

2.1 核密度估计方法概述

Emanuel Parzen［5］提出具有更高的精度和更连续的变化的核密度估计方法（KDE），可以针对直方图的这一缺点进行优化。核密度估计方法（KDE）认为某样本点s周围一定范围内的样本数量的大小会影响该点s的密度值。

图1 KDE示意图［5］

如图1所示，以点s为圆点，r为半径可以在空间中画出一个圆形，只有包含在这个圆形范围内的样本点才被认为是有贡献的，用dis表示范围内某点i与点s之间的距离，的比值越小，dis越大，则与点s相对距离更远的点对于点s的密度值贡献越小，对贡献的计算就是函数的表达。累计范围内所有样本点的贡献和影响，就得到了点s的核密度值λ(s)。

式中，λ(s)：点s处的核密度值；r：半径（或窗宽）；dis：点i到点s的距离；k ：核函数。

2.2 常用核函数分析

核函数有不同的表现形式，采用不同的核函数，会使样本点对中心点s的影响不同。但总的来说，核密度估计的基本原理决定了核函数是对称的，且在取值范围内积分为1，应用比较广泛的核函数有：

表1 常用核函数介绍

Uniform均匀核函数认为一定窗框内所有的样本点对中心点具有相同的贡献，因此赋予范围内所有的样本点相同的权重值，出现的核密度曲线概化程度较高。Triangle核函数认为范围内样本点对中心点的贡献（权重）随着距离的增大以线性的速度下降，可以呈现出细节变化更明显的核密度曲线。Epanechnikov核函数中，权重随着距离下降的趋势更加缓慢且连续，曲线也更加平滑。Gaussian核函数是单值函数，其像素点权值与距离成正比，图像不易失真；它没有边界，因此可以包含研究范围内所有的样本数据；它的核函数值随距离衰减，中心附近的样本点权重更大；它的傅里叶变换频谱是单瓣的，意味着高频信号无法污染平滑图像；同时Gaussian核函数具有可分离性。综合考虑以上优点，Gaussian核函数的应用非常广泛。

3 水上交通领域应用分析

3.1 距离度量方式的确定

内河航道中存在着许多不同的交叉口，造成了不同通航环境下的交通流分流，即使在不考虑通航环境差异化的前提下，利用根据网络距离度量方式的核密度估计来辨识长江干线的水上交通黑点，仍需要分析研究区域内所有交叉口的特殊衰减情况，通过交通流分流情况的不同，明确其特定的衰减系数。这是一个非常繁琐的过程。

当研究沿海水域的水上交通事故黑点问题时，需要考虑的因素又发生了变化。此时，可航水域覆盖的面积十分广阔，远远大于船舶船身所占面积。对航道的考量也不再使用其线性特征来表示，而认为其是一个“面”，即研究区域变成平面，而不是二维平面上的线性网格。此时度量两个事故点之间距离的方式更宜采用欧式距离度量方法，即两点之间的直线距离。同时不考虑核密度估计值跟随线型的交叉口进行某种程度的衰减，而认为在窗宽范围内，距离中心点相同距离的点的核密度估计值相同。

描述空间中任意两点之间的距离公式有很多。常用以下的几种方式来度量第k个交通事故与第q个交通事故之间的相似性［6］。其中，交通事故k=(xk1，xk2……xkp)，q=(xq1，xq2……xqp)。

欧氏距离（Euclidean distance）

应满足条件：

1）d(k，q)≥0 ，距离非负；

2）d(k，k)=0，对象所在位置为0点；

3）d(k，q)=d(q，k)，函数对称；

4）d(k，q)≤d(k，h)+d(h，q)。

当度量发生在航道中的两起水上交通事故之间的距离时，其环境是具有相似性的［7］。在密集的水网地带中，尽管船舶看似具有一定的可航水域，实际上对船舶操纵而言，航道仍然是线性的而非带状的。再加上现有航道大多为天然航道，自然弯曲或只部分经过人工改造，水网构造十分复杂。由此可以推断出网络距离在水上交通黑点辨识中的应用［8］。

3.2 模糊层次分析法（FAHP）分析事故严重程度

核密度估计函数中并没有考虑到事故严重程度对最终事故黑点辨识的影响。在数量相同的情况下，不同类型、不同严重程度、不同伤亡人数、不同财产损失造成的社会影响和危害程度也不同。因此，引入事故严重程度指数考虑事故严重性影响是非常有必要的，可以使黑点辨识结果更符合客观实际。

交通运输部《水上交通事故统计办法》［9］第六条中明确了如何划分水上交通事故等级，根据此条例，杜珊珊［3］等人、何茂录［7］等人依据事故被划分的事故等级进行梯度赋值（黑度值），即直接为不同等级的事故赋予不同的权重，详见表2。

表2 梯度赋值法

对此，本文在梯度赋值法的基础上，综合专家评分法和模糊层次分析法，确定各项水上交通事故指标的权重，使之计算的黑度值能挖掘和保留更多的事故细节信息，区分事件之间严重性的差别。

模糊层次分析法（FAHP）与层次分析法（AHP）的步骤基本一致。

（1）建立研究问题的层次分析结构

此处讨论用水上交通事故中不同事故指标对于事故结果的影响。层次分析构造如图2所示。

（2）构建判断矩阵

为了比较两元素之间的重要性，构建了由事故指标组成的判断矩阵（(fij)4×4）。其中，判断矩阵元素之间相对重要性的方法为，

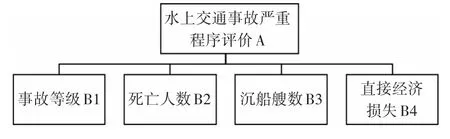
图2 层次分析综合结构图

通过匿名征集航运业内经验丰富的专家意见，采取问卷调查的方式，选取有效的问卷调查结果，得到的可靠判断矩阵如下：

表3 专家打分法构造A-B层判断矩阵(fij)4×4

（3）构造模糊一致矩阵

将上述判断矩阵变换为模糊一致矩阵。在判断矩阵（式2-2）的基础上构建一个新的矩阵M=(mij)n×n，其中，

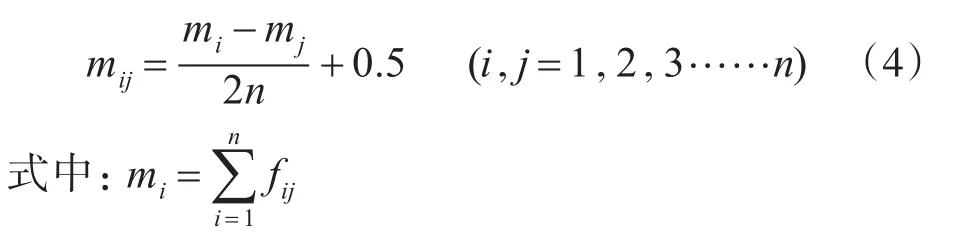
（4）层次排序

采用模糊一致矩阵从上而下，一层一层地计算本层针对上层某指标的重要性程度顺序。最后得到各项指标的权重。

表4 专家打分法构造A-B层模糊一致矩阵(mij)4×4

层次排序的方法有很多，方根法是比较常用的一种，

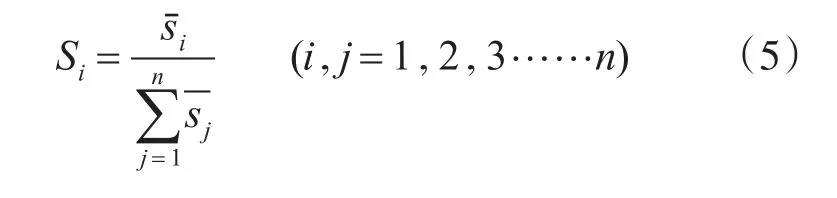
引入方根法，计算出表4的层次排序结果：

w0=S=(0.14583，0.35183，0.25117，0.25117)

即，各事故指标对应的权重如表5所示：

表5 各指标权重计算结果

对水上交通事故严重程度的评价，是一个多变量综合分析的问题。事故具体信息中，事故数量的度量单位是件；事故造成人员伤亡的度量单位是人；事故造成的沉船数量为艘；事故造成的直接经济损失的度量单位是万元，且通常数量级远大于其他指标。不同的单位、数值、数量级给多指标综合分析带来了很大的困难，为了去除影响，尽可能的展现事故的实际信息，需要对指标数据进行归一化处理。

均值法是用每个事故指标的值与该指标的平均值的比值来表示数据去量纲的结果，将数据等比例放大或者缩小到（0，1）的范围中，

用P值表示事故严重程度指数（为叙述和理解方便，简称“黑度值”），则P值的表达式为：

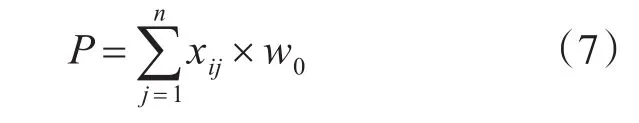
4 核密度估计的事故黑点辨别在深圳航道中的运用

在2003年至2014年间，深圳西部湾发生的水上安全事故一共434起。根据相关部门介绍，这些事故主要集中在该湾区的妈湾航道、蛇口航道等地。由于年代太过久远不具有参考性，本文节选2009-2014年共5年期间的事故数据进行实例分析。

4.1 建立交通事故空间数据库

通常来说，水上交通事故数据来源广泛且数据量巨大，共享化需求程度高，由于数据库存储对象为用于描述事故发生地地理位置及空间环境要素属性的空间数据，这一类数据与传统的文本及数表文件数据有很大差别，故现有关系数据库及文件系统管理模式已无法满足数据处理要求。因此，最理想的水上交通事故黑点辨识系统应具备空间数据库集成结构，使关系数据库能充分容纳空间数据与属性数据，提高空间数据与其他数据的兼容性，最终完全实现关系数据库管理系统在处理大量数据时应具有的快速、高效、准确的能力。

对于水上交通事故来说，其具备的一大特点便是空间属性强，具体来说，包括事故发生位置、分布情况等。随着计算机科学技术的发展，为进一步研究公路交通事故，提高事故风险大小的可读性，地理信息系统（Geographical Information Sys⁃tem，GIS）这一种功能强大的可视化分析软件便应运而生［10］。

对空间数据来说，有三类元素是其必须具备的。对象类与要素类最大的不同便是，前者为非空间实体，无法直接在底图上显示出来，但与地图各种元素关系密切；后者拥有空间实体，具体来说就是点、线、面三大元素类。要素数据集组成元素为一组相同空间参考的要素类，用来存储矢量数据［11］。同时，我们可以利用关系类对有所差异的要素类或对象类之间的联系进行区分与定义。另外，属性的定义域通过属性域来解决。2009-2014年深圳西部港区交通事故的空间数据库原始统计分析［12］，以便获取需要的详细信息，

（1）提取事故调查报告中的事故指标数据，包括事故等级、沉船艘数等；

（2）对事故等级、沉船艘数、事故伤亡人数、事故造成的直接经济损失等进行归一化处理；

（3）利用模糊层次分析法和专家打分法得到的指标权重，计算事故的严重程度指数（黑度值）［13］；

（4）将黑度值、坐标点数据导入ArcGIS中。

4.2 核密度估计算法实现

在计算对应坐标点的水上交通事故严重程度指数后，选取合适的核函数后，确定合适的窗宽，在ArcGIS上定义节点（距离通常取窗宽的1/10），计算所有单元节点的核密度估计值，然后计算所有单元节点核密度估计值，最后对单元节点按核密度估计值分类颜色渲染。

在ArcGIS中，以某起事故点为核中心，计算距离在带宽范围内各个节点距离可以使用要素属性表中的字段计算器（Field Caculator）。

按算法流程，可以利用Visual Basic语言对ArcGIS平台进行二次开发。计算所得核密度值如图所示。从图3中可知，红色实心圆点密集集中在某一区域中，即事故点的节点核密度值较高。虽然图中弱化了各红点之间的水域，但就研究区域而言，透明部分可能极小但并不为零，根据核密度估计的基本原则，这是因为事故对周边区域产生一定程度上的辐射影响，影响程度与距离成反比关系。

图3 交通事故数据点空间分布图

ArcGIS通过区分属性值对其进行分类，分类方法有：自然断点分级法、自定义间距分级法、等间距属性值分级、分位数分级、标准偏差分级法等。考虑到本文研究特点，为了更好的描述单元属性值的分布情况，选择标准偏差分级法作为本文分类方法。

经过对软件的不断调试，本文选择1/2倍标准偏差分级法，对所有单元节点的核密度估计值进行分类，并通过颜色渲染进行区分。中心值为均值，区间大小为1/2个标准差，如图4所示，即为分类显示结果。其中最小值为0，最大值约为26.583，核密度估计平均值为0.202，标准差为1.036。根据结果可得，单元的核密度估计值基本集中在均值左右，呈现对称分布的态势，符合标准偏差分级法的应用要求。

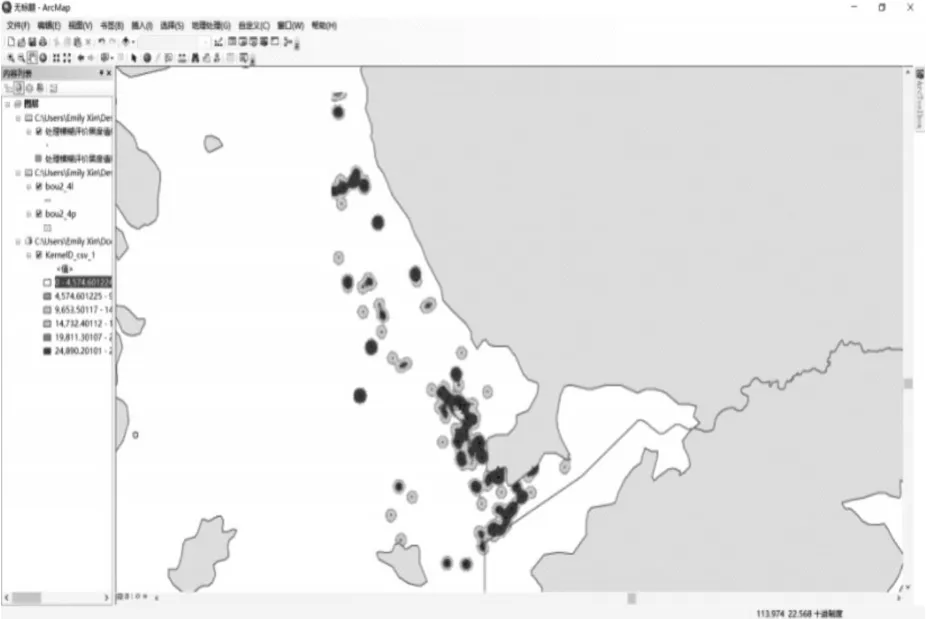
图4 核密度估计结果二维展示图

通过颜色渲染，对每个点的核密度估计值进行可视化表达，渲染颜色与估计值所在区间有关，局部渲染结果颜色深度与核密度值成正比关系，同时也能在一定程度上说明该地事故风险大小。

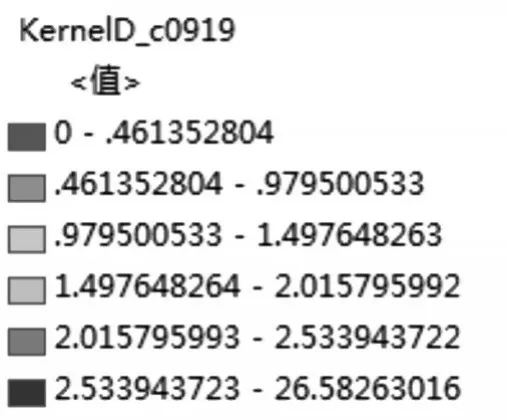
图5 标准偏差分级渲染指标

在ArcGISMAP中使用工具时，将“环境”选项中的范围一栏更改为更大范围或者与全国矢量图相同范围，实现事故数据处理结果和导入的全国矢量地图的衔接。具体效果添加事件点后如图6所示：

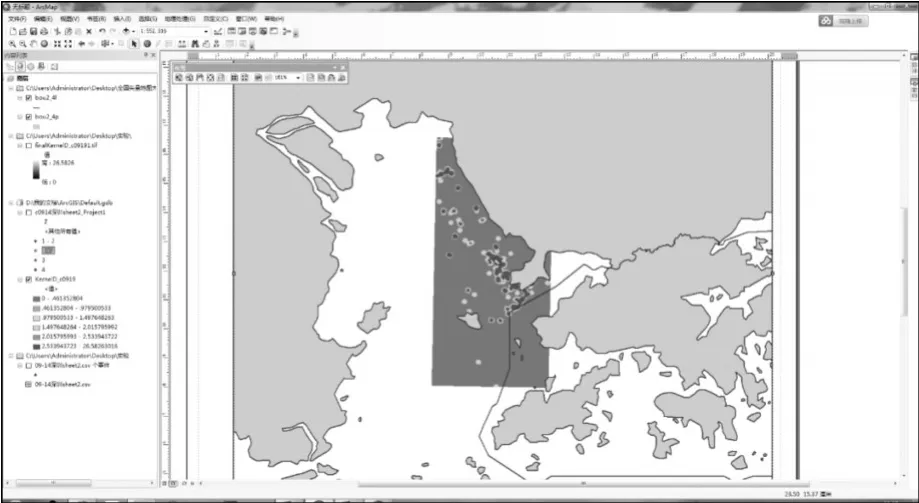
图6 标准偏差分级渲染结果二维展示

基于深圳海事局2009-2014年在辖区内统计记录的水上交通事故数据，结合在ArcGISDesktop软件中完成的核密度估计值算法的实现，得到的核密度估计值分布情况如图所示。从图中可以看出妈湾警戒区、大铲锚地、妈湾码头前沿水域渲染颜色以橘黄与红色为主，这类颜色深度说明，该区域核密度估计值较大，事故风险值较高。所得结果基本符合深圳实际交通安全情况。

核密度估计值的三维立体展示利用ArcMap，计算得到所有单元节点的核密度均值，平台会直接生成。shp格式文件，将其载入ArcScene中，考虑高程差异，设定参数，通过色彩填充来将二维的核密度值显示图像转化为三维图像。这种三维化的处理手段，提高了水上安全事故风险大小的界面可读性。为交通安全专家识别事故状况提供了感官上的帮助，可快速、高效地识别出对应区域的可疑黑点位置及其风险值。

图7 深圳西部港区水域核密度值立体空间展示

4.3 基于核密度估计的水上交通事故黑点辨识

根据图示核密度值的三维图像（如图7所示）可知，核密度值的高低直接与相应区域的事故安全水平对应，即：核密度值越高，该区域越容易发生安全事故，航道安全系数也越低。当此类安全性能较差的航道区域面积达到一定数值时，此航段便可认定为水上交通事故黑点。水上交通事故数越多，核密度值越大，H值表示发生事故次数的临界值。事故发生的原因是多方位的，包括通航环境、船舶自身条件、驾驶员因素等等，均会对水上交通安全造成影响，因此，判断H值的取值是十分复杂的，不同航道、不同时间、不同驾驶人，H值均会有所不同。所以，使用单一的绝对数指标去评价H值是不符合实际情况的，需要取待研究区域中所有的核密度值的相对比例数值大小来表示。

经过调试，本文最终决定按照核密度值由高到低的顺序对单元节点进行排序，排序在前5%的单元节点即为事故黑点。对深圳西部港区2009-2014年期间的163起水上交通事故数据进行以核密度为方法的事故黑点辨识后，最终识别出了6处水上交通事故黑点，辨识结果如图8所示。

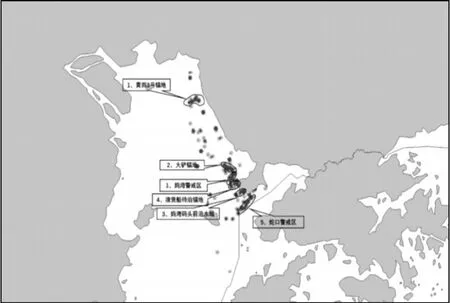
图8 黑点辨识结果

深圳港西部港区位于珠江口东岸，靠近香港特区，背靠珠江三角洲，包括蛇口等多个港区，是典型的潮流河口港。该水域的主流向大致为南北向与珠江河口一致。由于深圳西部港区航道狭窄、航路分叉较多、流态复杂，船舶交通流量很大，尤其VLCC受航行水域航道宽度、实际水深、潮流影响，交叉相遇的经常发生，避让关系复杂，操作难度很大，一旦判断失误，很容易发生险情。

应用本文所讨论的方法辨识黑点得到的结果与深圳西部港区的实际情况十分符合。深圳西部港区重点水域（蛇口警戒区周围），其是深圳港航行环境最复杂、船舶密度最大、水流流向变化最多的水域之一，再加上赤湾航道，该水域对驶相遇、追越、交叉相遇等多种局面均存在，航行情况十分复杂。蛇口航道、铜鼓航道出入口与主航道夹角较大，会受到主航道上接近南北向的涨落潮水横向推压，在端午节前后的龙舟水季节或大潮转急落水时，蛇口航道口门处有流速超过4节的横向急流［14］。

将核密度估计方法通过ArcGIS平台应用于水上交通黑点辨识中，直观的反映出安全性差的事故黑点区域，其发生的交通事故可能性大，是首先需要实施安全改造项目的目标区域之一。与深圳西部港区多年以来的实际通航环境情况作对比，可以发现核密度估计的结果是可信、可靠且有效的。