外接球的四种解法案例
2018-10-12海南省东方市东方中学王怀丹
□ 海南省东方市东方中学 王怀丹
□ 海南省东方市民族中学 张利平
球是空间几何中的重要几何体,也是普通高中数学课程标准实验教科书必修二的重要知识点之一。求一些简单几何体外接球的表面积、体积,以及与外接球有关的简单几何体的体积和距离等计算问题是高考考查的重点、难点和命题的热点,解决这类问题的关键在于确定外接球的球心位置,球心到几何体任一顶点的距离即为外接球的半径。因此,从观察空间几何体,认识整体图形入手,以我们熟悉的正方体、长方体为载体,推广到对正棱柱、棱锥的结构特征的认识和理解,由这些几何体的结构特征抽象出外接球的球心位置,寻找几何体中点、直线、平面之间的关系,把空间问题转化为平面问题,进而求出外接球的半径。
从近几年全国各省的高考试题来看,经常出现与外接球有关的问题,这一类问题在各省高考中得分率较低,大部分学生都感觉不知道如何下手。归根结底在于学生对空间问题的想象能力、推理能力和计算能力都有所欠缺。本文将结合自己在教学过程中的做法,从四道高考题中归纳出有关外接球问题的四种题型,进而推广出与外接球有关问题的四种具体解法,以便学生比较容易地掌握球的性质及与外接球的有关的计算问题。
案例一:求与长方体(正方体)外接球有关的计算问题
例1.(2007年天津卷理科第12题)已知各顶点都在一个球面上的长方体的三条棱长分别为1、2、3,则此球的表面积为__________。
【自主解析】:要求球的表面积,应先确定球心的位置,求出球的半径即可。
【答案】14π
【归纳】长方体(正方体)外接球的球心位置即长方体(正方体)体对角线的中点,长方体(正方体)体对角线长的一半即为外接球的半径,因此,求外接球的半径即可转化为求长方体(正方体)的体对角线长,再运用球的表面积公式或体积公式计算出结果。
正三棱柱、正五棱柱没有体对角线,我们不能像例1那样说“体对角线长的一半即为外接球的半径”,那么,此类型题怎么解决呢?大家知道:正方体是特殊的正四棱柱,还可以这样思考:正四棱柱的中心即为正四棱柱外接球的球心,也就是上下底面中心连线的中点,由球心、底面中心及同底面一顶点连线构成直角三角形,将空间问题转化到平面直角三角形中求解,再运用勾股定理求解出半径。由此可以延伸到题型二。
案例二:求与正棱柱外接球有关的计算问题
例2.(2010年海南卷理科第10题)设正三棱柱的侧棱垂直于底面,所有棱长都为a,正三棱柱的顶点都在一个球面上,求该球的表面积为( )。
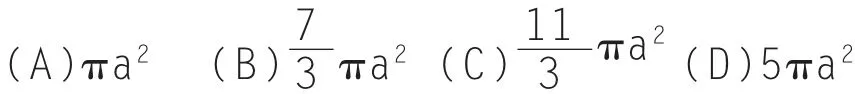
【自主解析】要求球的表面积,应先确定球心的位置,知道球的半径即可。
如图1所示,P为三棱柱底面中心,O为球心,易知:
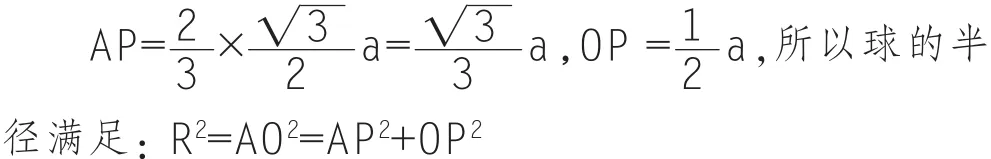
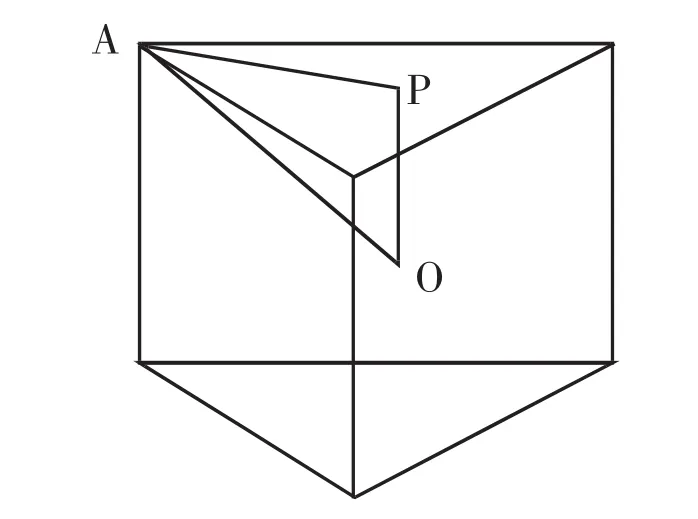
图1

【答案】 B
【归纳】求与正棱柱外接球有关的计算问题,正棱柱的外接球的球心就是上下底面中心连线的中点,连接球心、底面中心及同底面一顶点连线构成直角三角形,将空间问题转化到平面直角三角形中求解,运用勾股定理求解出半径,再由球的表面积公式或体积公式计算出结果。
案例三:求与棱锥外接球有关的计算问题
例3.(2012年海南卷理科第11题)已知球O是三棱锥S-ABC的外接球,等边三角形ABC的边长为1,SC是球O的一条直径,SC=2,则棱锥S-ABC的体积为( )。
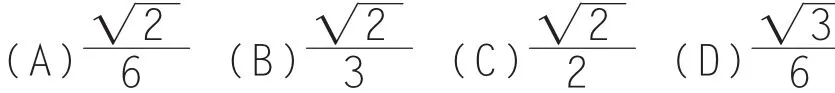
【自主解析】要求三棱锥S-ABC的体积,可以转化为求三棱锥O-ABC的体积。
因为三棱锥S-ABC和三棱锥O-ABC有共同的底面△ABC,球心O为SC的中点,所以三棱锥S-ABC的高为三棱锥O-ABC高的2倍,即VS-ABC=2VO-ABC
如图2所示,在三棱锥O-ABC中,其棱长都是1,取等边三角形ABC的中心为D,点D即为底面△ABC外接圆(即截面圆)的圆心,球心O在点D的正上方,则OD⊥面ABC。

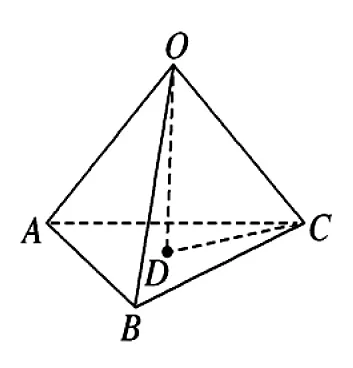
图2
【答案】 A
【归纳】我们可把这种题型的思路应用于求与棱锥外接球有关的计算问题,即先找出棱锥底面外接圆(即截面圆)的圆心,在其“正上方”或“正下方”确定球心O的位置,将空间问题转化到平面直角三角形中求解,再运用勾股定理解出答案。
案例四:构造法
例4.(2012年辽宁卷理科第16题)在正三棱锥 P-ABC 中,点 P、A、B、C都在以 3 为半径的球面上,且三棱锥的侧棱PA、PB、PC两两互相垂直,则球心到截面ABC的距离为__________。
【自主解析】因为正三棱锥的侧棱PA,PB,PC两两相互垂直,所以以PA,PB,PC为棱构造成正方体(如图3所示),体对角线PD的中点即为正三棱锥P-ABC的外接球球心O,球的半径PD=

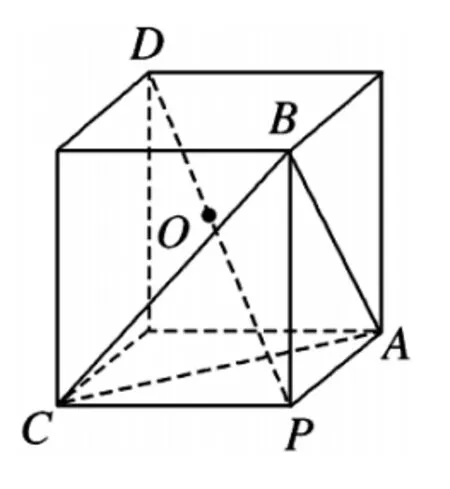
图3
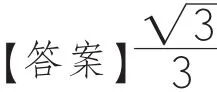
本题考查学生对空间问题的想象能力和计算能力,我们可以将该问题“补全图形”到正方体中解决。此题若用一般的解答方法,同题型三,应先确定球心的位置,求出球的半径即可;而作为填空(选择)题,可以用更为简便的解答方法,此题应注意到“三条侧棱两两互相垂直”,可以联想到过正方体(长方体)的一个顶点相邻的三条侧棱,AB、BC和AC可以联想到过正方体(长方体)的同一顶点三个侧面的对角线,很容易想到构造成一个正方体(长方体),运用题型一马上就能得出答案。
【归纳】若三条侧棱两两相互垂直,或一侧棱垂直于底面且底面为正方形或长方形,则像这样的几何体可构造出正方体或长方体,运用归纳一,那么,所要求的问题就比较容易解决了。
总之,对解决一些简单几何体外接球有关的计算问题的求法,能根据已知条件做出图形,由图形想象出直观形象,通过对几何体的具体结构特征的认识和理解,从而寻找几何体中点、直线、平面之间的关系,确定球心的位置,把空间问题转化为平面问题,进而求出空间几何体外接球的半径。空间几何中蕴含着丰富的思想方法,如补形法、构造法和转化思想等,在解题过程中常常具有规律性,只要不断地总结,就能不断地提高。
