模拟降雨条件下黄土区SCS模型的参数率定

2018-10-12邓景成穆兴民赵广举孙文义

水土保持研究 2018年5期

邓景成，高鹏，2，穆兴民，2，赵广举，2，孙文义，2，田鹏，3

(1.西北农林科技大学黄土高原土壤侵蚀与旱地农业国家重点实验室，陕西杨凌 712100； 2.中国科学院水利部水土保持保持研究所，陕西杨凌 712100； 3.西北农林科技大学资环学院，陕西杨凌 712100))

水资源短缺、水土流失等问题因其关系人类生存发展备受社会关注，而暴雨形成的超渗产流是黄土区水土流失的主要动力来源，因此，开展径流模拟的相关研究，是进行土壤侵蚀预报和水土流失防治的重要基础。SCS模型[1]是美国农业部水土保持局研制的用于计算给定降雨条件下一定区域地表径流的经验模型，因其结构简单，仅需一个反映地理和气候因子—初损率λ和一个反映土壤型、土地利用/覆被状况以及前期土壤湿度的参数—径流曲线数CN[2-3]，被广泛应用于许多国家的流域水文模型[4-5]。SCS模型中初损雨量与流域最大入渗量的比值定义为初损率，取值范围为0.095～0.38，通常取标准值0.2[2,6]。近年来许多研究表明不同地区初损率取标准值时模型模拟精度不能满足实际应用。Shi等[7]运用事件分析法对中国三峡库区王家沟小流域初损率进行了率定修正，发现流域初损率变化在0.01～0.015 4，选用0.05为初损率模拟效果最佳。Woodward等[8]通过分析美国23个州307个小流域28 301次降雨事件观测数据发现，不同流域以及同一流域不同降雨事件初损率取值均不同，且小于标准值。不同区域，初损率λ取值会有所差异，甚至是同一地区不同坡度等级也有差异[9]。因此，许多学者在应用SCS模型时都对初损率λ进行了修正[4,9-13]。

径流曲线数CN值由美国土壤保持局提供的CN查值表得到，由于黄土区土壤水文条件、土地利用方式等与美国地区的差异，在运用查值表时有效性受到影响[14]。CN值是SCS模型中一个重要的参数，对径流计算结果影响很大。Boughton[15]的流域试验研究表明CN值变化±10%就会引起径流量计算变化+55%和-45%，因此CN取值对于准确计算区域地表径流量有重要意义。关于黄土区SCS模型参数的率定进行了许多研究，张钰娴等[9]通过分析黄土区62场实测降雨资料对初损率λ进行了定量分析，结果表明，标准值0.2仅适用于黄土丘陵缓坡地，随坡度增大λ相应减小。周淑梅等[10]的研究也表明黄土区桥子西沟小流域初损率为0.1时模拟效果更好。尽管针对黄土区SCS模型的修正已有许多研究，但关于不同土地利用类型在运用SCS模型时的研究较少。本文通过杨青川流域进行的22场人工模拟降雨资料，分别对草地和裸地在运用SCS模型模拟径流深进行了初损率λ和径流曲线数CN的率定。

1 基本原理

SCS-CN模型是基于水分平衡方程

p=Ia+F+Q

(1)

两个基本假设：一是假设流域内实际径流量(Q)与可能最大径流量的比值等于实际入渗量(F)和流域最大入渗量(S)：

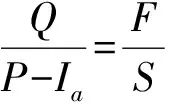
(2)

二是假设初损量(Ia)与流域最大入渗量(S)成比例：

即Ia=λS

(3)

(1)，(2)，(3) 解得：

(4)

式中：P表示流域内总降水量(mm)；Ia表示初损雨量(mm)；Q表示流域内实际径流量F表示流域实际入渗量(mm)；S表示流域最大入渗量(mm)；λ为初损系数，是一个区域参数，其数值主要取决于地理和气候因子，取值范围为0.095≤λ≤0.38；λ值的大小是影响模型产流模拟的重要因子，标准值取0.2。流域最大入渗量S通过以下公式计算：

(5)

CN值是一个反映土地利用、土壤类型、水文条件和前期土壤湿度的综合性指标，范围在0～100。SCS模型根据土壤最小下渗率和土壤质地，将流域水文土壤类型划分为A，B，C，D共4类，入渗能力依次降低。在一定的水文类型，覆盖类型和管理方式下，水文条件好，土壤一般产流能力低，通常根据样方的植被密度和地表残余物覆盖度来估计。前期土壤湿度由降雨前5 d累计降雨量确定即前期降水指数API(Antecedent Precipitation Index)，分为AMCⅠ(干旱)、AMCⅡ(正常)和AMCⅢ(湿润)3种状态，分别对应CN1，CN2，CN3。用户可根据研究区的土壤类型、土地利用和土壤湿度状况由查值表获取CN值。基于美国的植被状况、土壤类型、产流机制与我国的差异，在应用SCS-CN模型时要根据研究地的实际情况对CN值进行修正。

2 材料与方法

2.1 研究区概况

研究区位于距陕西省延安市吴起县城南20 km左右的杨青川流域，坐标为东经107°52′47″，北纬37°2′49″，杨青川流域属半干旱温带大陆性季风气候，地貌属黄土高原丘陵沟壑区。流域内成土母质为黄土，土壤以黄绵土为主，土壤颗粒以细砂粒和粉粒为主(80%左右)，土壤容重为1.23 g/cm3，总孔隙度55%～60%，最小入渗率5.0 mm/h,属于B类土壤。试验共设草地、裸地两种样地，草覆盖度大约为55%。试验小区详细立地条件见表1。试验采用两侧对喷式降雨装置模拟人工降雨。喷头高度大约为6 m。通过更换喷头出水孔的孔径来调整降雨强度。降雨装置受风的影响较大，因此选择在清晨5：00—6：00进行试验，以减小风对试验结果的影响。试验时间安排在2015年8月19日至9月26日，属于植被生长期。降雨前用烘干法测定的土壤前期含水量结果为：0—50 cm平均含水量为20.45±0.13%；0—100 cm平均含水量为17.18±0.14%，综合小区的前期降雨影响，确定土壤前期湿度等级为AMCⅢ级。试验在草地和裸地4个小区间轮流进行，尽量避免试验过程中对草地的人为扰动，裸地小区采取翻晒、整平处理。小区沿对角线布设3个翻斗式自计雨量筒，记录每次试验的降雨量。降雨时，记录产流开始时间，定时用塑料桶采集径流泥沙样，时间间隔为1 min。

表1 模拟降雨径流小区布设情况

2.2 标准SCS模型径流模拟

取标准初损率λ=0.2，则初损雨量Ia=0.2S。前期对试验地含水量测定确定属于AMCⅢ等级，Huang等[13]的研究表明在黄土高原地区应用SCS模型时应对CN值进行坡度修正，根据公式(6)和(7)，结合土地利用方式和土壤类型等级选用CN2进行坡度修正。依据表2查算得试验小区草地和裸地的CN2值分别为65，82。运用公式(6)对CN2进行坡度修正得到CN2′，再利用公式(7)计算出前期湿度AMCⅢ条件下的径流曲线数CN3′。最后用公式(4)和(5) 计算出初损率为标准值0.2时得到的模拟径流深。

(6)

(7)

式中：CN2；CN3为AMCⅡ；AMCⅢ条件下的径流曲线数；CN2′、CN3′为坡度修正后的径流曲线数；α为坡度百分比(%)。

表2 不同湿度等级下不同土壤类型和土地利用类型CN值[16]

2.3 参数敏感性分析

参数率定的目的是进行敏感性参数的率定。所以,参数率定前必须对模型参数进行敏感性分析。初损率λ和径流曲线数CN是SCS模型中的两个重要参数。本文选2个坡度下的草地各一场实测降雨资料,通过固定模型其中一个参数,改变另一个参数的方法,对参数λ和CN进行敏感性分析，并通过弹性系数比较两个参数敏感性强弱，定义为径流变化率与某一参数变化率的比值。弹性系数绝对值越大表明参数敏感性越强。

(8)

式中：εi表示参数的弹性系数；i表示参数初损率和径流曲线数；ΔQ表示模拟径流变化率；Δi表示参数变化率。

3 结果与分析

3.1 λ取标准值时模拟径流深与实测径流深比较

根据SCS标准模型，取λ=0.2，模拟计算草地的12场降雨和裸地的10场的径流深，结果见图1。从图中可以看出，草地和裸地模拟计算得到的径流深均小于实测径流深，两者的决定系数R2分别达到了0.98，0.97，表明根据SCS模型模拟的径流深就相关性和变化趋势而言，效果较好。计算均方根误差RMSE和相对误差RE，草地分别为2.21，23.9%，裸地为5.41，17.51%，表明模拟值相较于实测值有相似的变化趋势，但误差量较大。图2反映了模拟径流深与实测径流深的比值图，由图可看出比值偏离1∶1线较大，离散程度较高，且均位于直线下方，表明模拟径流深相比实测径流深偏小。模拟值均偏小说明，根据模型计算过程中，初损雨量取值较大，即Ia=λS中的λ取值偏大，导致模拟的径流深偏小。因此标准的SCS模型不能准确预测黄土区的坡面产流过程。针对模型的相关参数进行适当修正优化尤为重要。

3.2 参数敏感性分析

对参数λ进行敏感性分析时，λ取值范围为0.095～0.38，取λ=0.10，0.13，0.16，0.19，0.22，0.25，0.28，0.31，0.34，0.37计算模拟径流深；对参数CN进行敏感性分析时，固定参数λ(标准值0.2)，CN值以1为步长，取CN=60，61，62，…，70计算模拟径流深。图3显示了在不同坡度条件下，模拟径流深随参数λ和CN的变化关系，初损率λ增大0.03，模拟径流深相应减少11%～41%;CN值增大1，模拟径流深增大5%～11%，计算不同坡度下弹性系数得ελ=-5.2，-4.8，εCN=2.73，3.41，比较弹性系数绝对值发现径流深对初损率λ的反应比较敏感，对CN值敏感性次之，但也表现出较强的敏感性。因此，模型中的两个参数都是敏感性参数，需要进行适当的修正率定。

图1草地和裸地模拟径流深与实测径流深比较

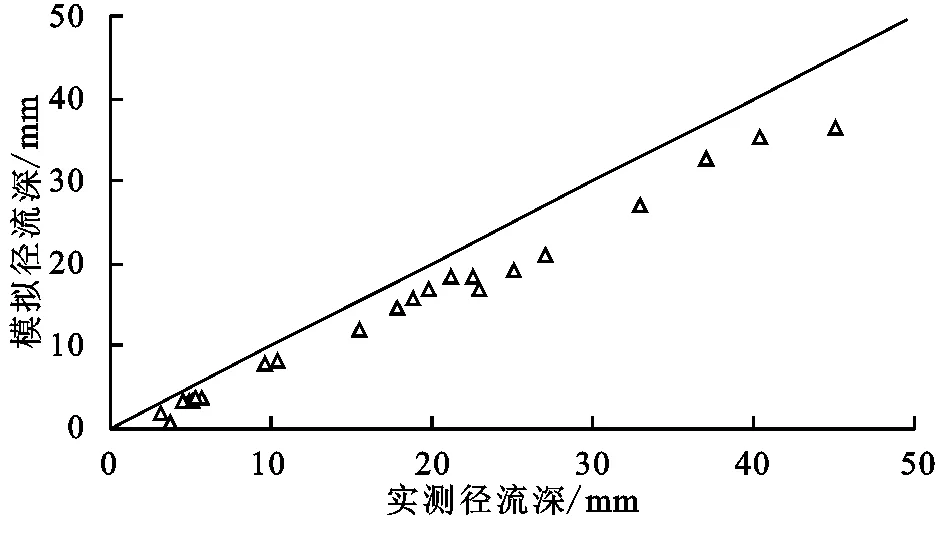
图2初损率取标准值时模拟径流深与实测径流深比较

3.3 初损率λ的优化率定

对初损率λ率定时，参数CN值按标准SCS模型取值，即草地和裸地分别为65，82，然后对λ进行优化。λ取值范围为0.095～0.38，以0.01为步长，依次代入公式(4)计算径流量模拟值，以均方根误差RMSE、相对误差RE和纳什系数NSE作为评价指标。表3列了λ取部分值时计算的各评价指标，从表中可以看出对草地而言，当λ取0.15时，RMSE，RE最小，相比于取标准值0.2，RMSE由2.21减小为0.87，RE由23.9%减小为7.16%，纳什系数NSE也由83.5%提高为97.42%；裸地则是在0.05时，RMSE，RE最小，为1.98，5.49%，NSE最大为94.51%，经过优化修正得到草地初损率取0.13，裸地取0.03时效果最好。将经过修正后的λ代入公式(4)计算地表径流，与实测径流深作比较(图4)，草地其均方根误差RMSE减小为0.68，相对误差RE减小为5.69%,纳什系数增大为98.45%；裸地其均方根误差RMSE减小为1.69，相对误差RE减小为4.68%，纳什系数NSE增大为95.99%。优化λ后模拟的模拟精度显著提高，这表明了在黄土丘陵沟壑区应用标准SCS模型进行径流估算时，由于土壤性质、土地利用类型和气候条件等的差异，必须对初损率λ进行区域适用性评价，以得到适宜于研究区域的λ值。

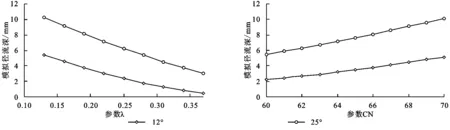
图3参数敏感性分析

3.4 径流曲线数CN的优化率定

CN值也是影响模型模拟径流深的敏感性参数。为了进一步提高模型的精度，在草地和裸地λ分别取0.13，0.03的基础上，以1为步长对径流曲线数CN值进行优化，同样以RMSE，RE和NSE作为评价指标，得到草地和裸地CN取值为65，83。草地经过RMSE，RE和NSE判定发现原值65在计算模拟径流深时效果最好，裸地则取83模拟效果更好，均方根误差RMSE由1.69减小为1.50，相对误差RE减小为4.31，纳什系数NSE更高为96.83%。裸地优化CN值后模拟径流深与实测径流深比较见图5。从图6可以看出，与参数率定前比较，标定后的模拟值更靠近1∶1线，其离散程度显著降低。表明标定后的模型更适合预测本地区的降雨资料。

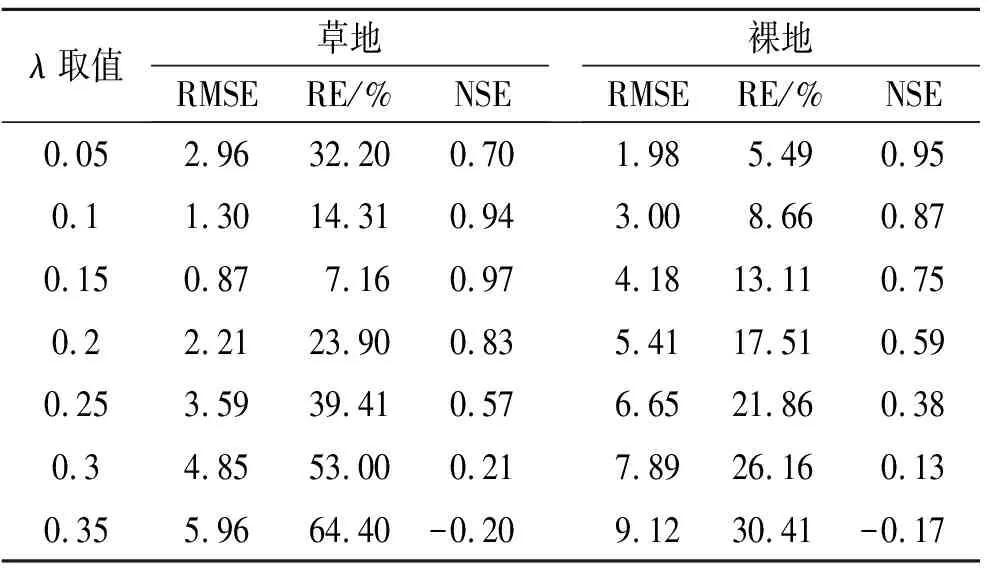
表3 参数λ取不同值时草地和裸地各评价指标

图4优化λ后的草地和裸地模拟径流深与实测径流深比较

图5CN值修正后裸地实测径流深与模拟径流深比较

图6λ与CN修正之后模拟径流深与实测径流深

4 结论与讨论

4.1 讨论

关于SCS模型在不同地区适用性问题已有许多学者进行了大量研究[4,9,10,12]。但一般都通过分析实测降雨资料进行研究[9,14]，考虑到野外收集降雨径流资料的困难与误差性，本文则通过人工模拟降雨试验，严格控制试验参数，相对增加了所测数据的准确性以及试验结果的可靠性。同时本次研究对SCS模型的两个控制参数初损率和径流曲线数都进行了敏感性分析以及参数率定，使得模型模拟结果与实测值拟合程度更高，进一步增加了模型在试验样地的适用性。由于试验经费以及试验操作的复杂性，使得样地只能局限于研究流域的部分可操作区域，对于流域其他土地利用类型的应用无法确定，因此大尺度模型的改进与应用尚须进一步研究。