萤火虫优化和随机森林的WSN异常数据检测*
2018-10-12许欧阳李光辉
许欧阳,李光辉,2,3+
1.江南大学 物联网工程学院,江苏 无锡 214122
2.江苏省无线传感网高技术研究重点实验室,南京 210003
3.物联网技术应用教育部工程技术研究中心,江苏 无锡 214122
1 引言
无线传感器网络(wireless sensor network,WSN)的构成单元是大量低成本、微型的传感器节点,可以感知网络部署区域内的各种数据信息,进行数据样本的采集、处理以及传输,特别适宜于无人值守或恶劣环境的监测。WSN目前在许多领域都有所应用,如工业控制、智慧农业、医疗监测、基础设施健康检测以及环境监测等。然而,节点自身的软硬件故障、电量耗尽或者部署环境遭遇突发事件(如强降雨、森林火灾或者危险品泄漏)等因素常常导致节点采集的数据明显地偏离正常数据形态。这类数据称为离群数据或异常数据。及时准确地检测出传感器数据流中的异常数据,不论是对于外部事件的实时监测还是无线传感器网络本身健康状态的监测都具有十分重要的意义。
近年来国内外对于WSN异常数据检测方法的研究已有诸多成果[1-4]。WSN异常数据检测方法大致可以分为5类:基于统计的方法、基于最近邻的方法、基于聚类的方法、基于分类的方法以及基于频谱分析的方法[5]。姜旭宝等人[6]提出了一种基于变宽直方图的数据异常检测算法,将动态感知数据以数据融合的方式聚合成为变宽的直方图并执行检测过程,该方法可以避免不必要的数据传输耗费。实验表明该方法在拥有较好检测性能的同时降低了通信开销。文献[7]提出批处理式的1/4超球面支持向量机异常检测算法,超球面支持向量机训练速度快,支持向量少。该检测方式需要每一个子节点将采集的数据通信传给父节点,然后集中在父节点执行异常检测算法,节点间要进行大量数据的传输,资源耗费较大。于是Rajasegarar等人[8]通过分布式的超球面支持向量机对传感数据进行检测,在每个子节点和父节点上分别执行局部异常检测,然后子节点仅需将它们的局部半径传给父节点,父节点计算得到全局半径,接下来在子节点上用全局半径执行异常检测,大大降低了花费在节点通信的资源,检测效率因而得到提高。以上3种方法都在资源耗费方面做了工作,但在检测精度方面以及模型自适应方面还有待提高。Zhang等人在文献[9]中利用超球面支持向量机(sup-port vector machine,SVM)在WSN中执行在线异常检测,提出了自适应离群检测技术(adaptive outlier detection,AOD),并实现了在短时间内对所收集到的数据的状况进行判断,不同于文献[7]中的批处理技术,其体现了实时的特点,但对模型的构建未考虑集成思想,后续更新会使得未来的模型适应度不够强。Hill等人在文献[10]中提出了在流数据中用多层感知器作为预测器得到下一时刻测量值的预测值,并以预测值和模型残差等参数计算预测区间(prediction interval,PI),通过比较实际值与PI的关系进行异常检测。该方法在异常数据相对较少的情况下性能理想,一旦连续出现较多异常值,模型的精度会受影响。
Zhou等人[11]提出了“部分或许优于整体”的选择性集成(selective ensemble,SEN)思想并将其用在了神经网络上,只在集成模型中选取部分精度高,差异度大的基分类器,得到至少不亚于原始模型的性能;丁智国等人[12]基于SEN使用生物地理学优化算法(biogeography-based optimization,BBO)实现了对集成的剪枝,用较少的个体分类器获得和原始集成相同,甚至更好的泛化性能,同时降低系统的存储和计算开销。该方法是SEN的应用,但在基分类器的选取以及选择性集成优化算法方面有待改进。
随机森林(random forest,RF)模型训练时采用随机采样,有泛化能力强,模型方差小等优点。因此,本文结合RF与SEN思想,提出了一种基于MBGSO优化RF的WSN异常检测算法,该算法在BGSO中引入变异机制,使得它较BGSO有着更好的寻优能力,该算法可应用于特征选择算法以及集成分类器的规模缩减中,ARF(adaptive updating random forest)则在目标分类检测领域应用较多,且在检测过程添加了模型更新机制,可随时间的推移执行模型自适应更新,比原始RF模型更加适应当前数据。因此,检测效率和准确性均有提高。将以上两者相结合,由于优化算法对集成规模大小的缩减,使得检测算法应用在WSN数据异常检测中所耗费的时间更少。
2 预备知识
2.1 决策树与随机森林
决策树(decision tree)是一种简单并广泛使用的分类器,RF中以CART(classification and regression tree)作为基分类器,并结合了Bagging思想[13]和随机特征子空间,集成所有子分类器,Breiman在文献[14]将RF表示为{ }h(X,θk),k=1,2,…,k,算法如图1所示,k为决策树数目,θk为具有独立同分布的随机向量,该随机向量即体现了bootstrap训练样本选取和划分属性的随机选取这两个随机因素。
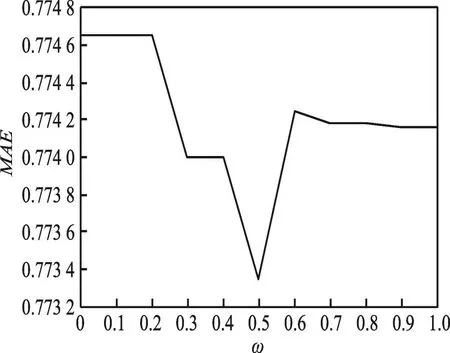
Fig.1 Scheme of RF algorithm图1 RF算法示意图
定义随机森林的边界函数mr如式(1),两项分别为分类正确的概率和分类为非正确类概率的最大值,鉴于检测时分为两类,因此后一项是对立类。Breiman通过大数定律给出了随机森林误差收敛定理,如式(2),结合决策树平均强度s以及决策树间平均相关度ρˉ,得出泛化误差上界大小PE*≤ρˉ(1-s2)/s2。误差上界的存在使RF具有良好的防过拟合能力,也是本文选取RF进行选择性集成的原因之一。本文后续优化工作所需的s和ρˉ可由袋外数据估算,具体计算过程参见文献[14]。
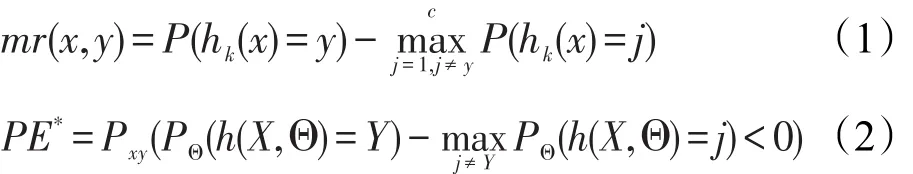
2.2 选择性集成学习
集成学习整体模型的泛化性能依赖于子分类器的多样性和分类强度,对于选择性集成,即通过提取一个比原始规模更小的子集成,以取得至少不低于甚至高于原始集成的性能。文中异常数据检测的过程实际是对未知样本标签的分类,确定它是正常或异常是二元分类问题,标签Label={ }-1,+1中的正负值分别表示正类样本和负类样本。以下简要介绍选择性集成思想[11]。
假定测试样本集的大小为m,每个子分类器对未知样本进行分类,并采用多数投票方式得到该样本的集成分类结果。集成整体误差如式(3)所示,其中eoj∈{-1,+1},j∈{1,2,…,m}。coj=sign(sj)表示集成模型对第j个测试样本的检测结果,其中sj与sign(x)分别为投票结果和指示函数。
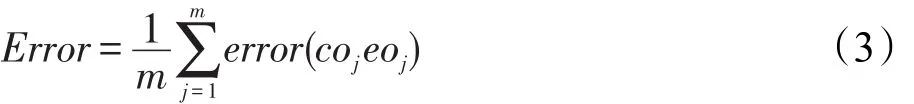
在此假设第k个子分类器不参加最终的投票表决,则为选择性集成,第j个测试样本的检测输出以及误差分别表示如式(4)和式(5)所示,可知Error′≤Error成立,详细证明过程可参看文献[11]。
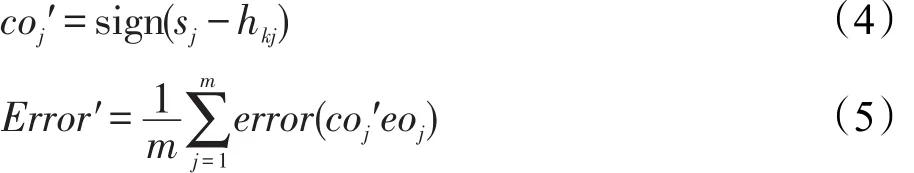
2.3 人工萤火虫优化算法
文献[15]通过模拟自然界中萤火虫发光行为提出了人工萤火虫优化算法(glowworm swarm optimization,GSO),搜索空间中的每个萤火虫表示所优化问题的一个可行解,每只萤火虫都拥有自身的感知半径通过式(6)转换为荧光素值,个体亮度与所处位置的目标函数值相关,亮度越大,目标函数值越优。并于迭代中通过式(7)选取个体移动目标,更新决策半径。不断迭代使得某些萤火虫发光越强,吸引力变得越大,最终绝大部分的个体萤火虫都聚集到最亮的个体周围,进而寻找到最优解,具体公式如下:
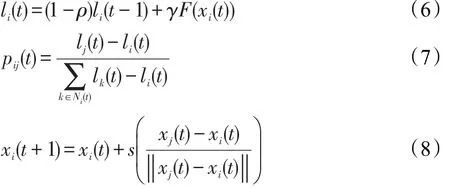
3 MBGSO选择性集成ARF的异常检测算法
本文将MBGSO与RF两者相结合,提出了一种新的WSN异常数据检测算法。由前文中RF模型的泛化误差PE可知,要提高集成模型的性能,必须提升个体分类器的分类强度并同时增强分类器之间的多样性。MBGSO算法适应度函数fitness(CE)的设定借鉴文献[16],为防止最终得到的子集成规模太小,对RF算法的收敛性造成影响,加入原始集成大小N预防过剪枝。如式(9)所示:
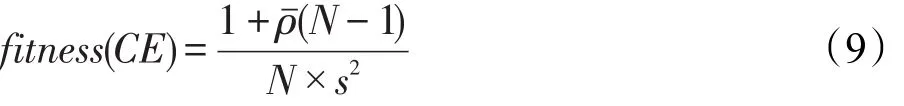
3.1 基于MBGSO算法优化RF集成模型
要对RF进行选择性集成,举个例子,假设一个RF模型有100棵决策树,要对该集成进行优化,实际是关于这100个个体的组合优化问题,属于离散性问题。然而,原始GSO针对的是连续型问题,且在寻优时收敛速度慢,易陷于局部最优。因此对于组合优化问题,文献[17]对传统GSO进行了改进,提出离散型萤火虫算法(discrete GSO,DGSO);Li等人[18]提出二进制萤火虫算法(binary glowworm swarm optimization,BGSO),不再使用GSO中的位置更新公式,借鉴高斯分布的思想构建高斯变异概率映射函数,将萤火虫个体位置映射为位变化的概率。BGSO在对集成模型进行优化时,会出现效果不够理想,过早收敛等问题,因此,本文在BGSO[18]基础上引入变异思想进一步提升了优化能力。
算法中对个体使用0、1编码,第i只萤火虫可以表示为xi=(xi1,xi2,…,xid),d为编码长度,在此即为所需优化的RF原始集成规模,个体初始位置xit(t)随机选取。
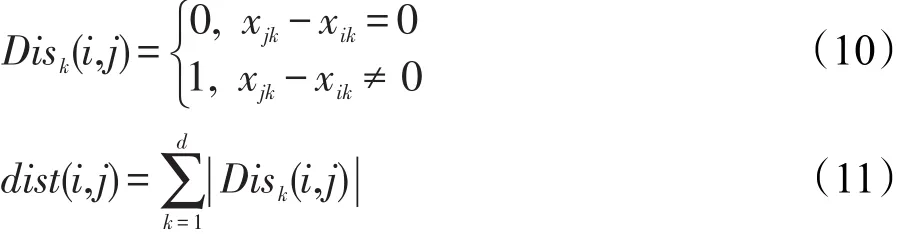
传统GSO中的距离采用欧氏距离,鉴于该问题的离散性质,对于某棵决策树是否被选取,只能是0或1,因此使用式(10)和式(11)计算两个萤火虫在第k维上的距离,并用汉明距离表示萤火虫i与j之间的距离。萤火虫i第k维上的位移sik定义如式(12)所示,lf为学习因子,rd为[0,1]内随机数。
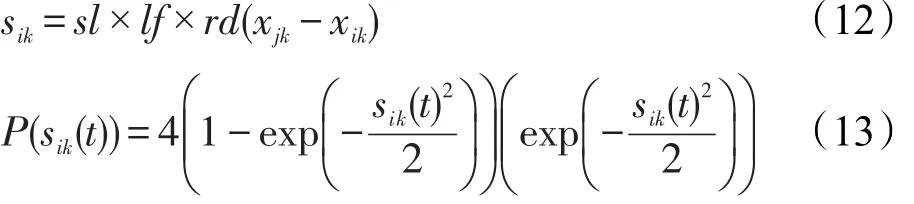
在进行目标函数值与荧光素值的转换和邻域移动目标选择时方式不变,在位置更新时使用式(13)替换原有方式。构建概率映射函数并修改萤火虫位置更新公式分别如式(14)和式(15)所示,此二式对应着sik(t)<0或sik(t)≥0时的新的位置更新方式。
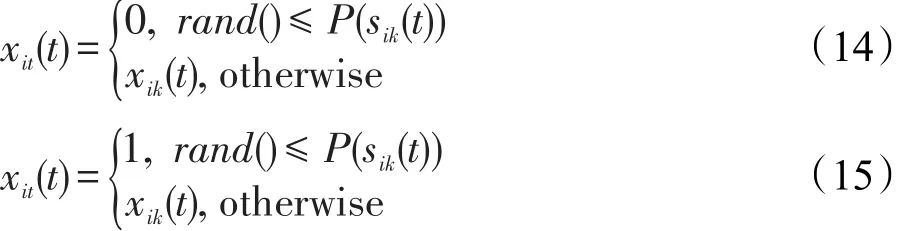
本文在算法迭代过程中引入个体变异,设置一个变异概率阈值θ,若rand>θ,则对当前个体进行以下操作:随机生成一个取值区间为(0,1)的d维向量r,变异公式参数p1、p2同属于0到1之间,通过式(16)更新个体中每一维的取值,即对比r中每一维的取值与p1和p2的大小关系,来决定当前维的值是否变化、转移或是取反,最终完成对个体位置的变异;反之,若rand<θ,则跳过这个步骤继续进行迭代。
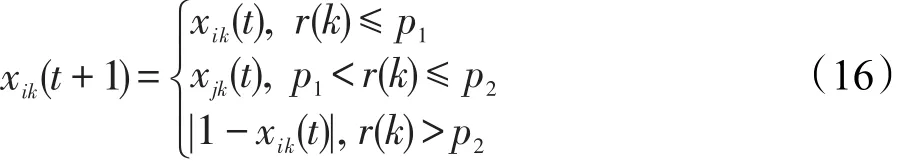
MBGSO算法优化选择RF子集成的伪代码如下所示。
算法1MBGSO(X,N,t,theta,ds,p1,p2,rf,itermax)
输入:数据集X;萤火虫数目N;当前迭代次数t;变异概率theta;决策半径ds;变异公式参数p1、p2;训练所得检测模型rf;最大迭代次数itermax。
1.初始化算法各参数;
2.以式(6)作为算法目标函数;
3.当t 4.对除第i个萤火虫本身外的所有个体,求它们到i萤火虫的汉明距离distance; 5.选取distance 6.通过传统GSO算法中的轮盘赌方法计算i的移动方向; 7.ds的更新依然以原先方式进行,以概率映射函数(式(13)至式(15))对个体的位置进行更新; 8.若rand()>theta,通过p1、p2使用式(16)对部分个体进行变异操作; 9.记录当前迭代最优值vcurrent以及最优子集成组合rf-se; 输出:迭代完成时的最优值以及rf-se。 首先执行RF算法训练选取的WSN数据集得到检测模型,并使用本文所提MBGSO算法优化RF原始集成模型,对原始集成进行选择性剪枝获得最优子集成RF_SE,此时的子集成即可代替原始模型对后续的待测样本执行异常检测工作。 MBGSO-ARF检测算法在MBGSO-RF基础上增加了自适应更新的过程,在此设定数据块大小size_block为1000,对WSN测试数据集以size_block为单位大小进行读取,每当子集成RF_SE检测完size_block待测样本后,使用如下方式变更Buffer和validate内的数据并对当前集成模型进行更新。 设定Buffer和validate的大小分别用于存储模型更新样本以及选择性剔出集成中的某些子分类器。Buffer是通过泊松分布随机数在待测样本集合中随机取样得到,而validate则为数据块中大小为size_val的小样本集。并使用validate小样本集对当前集成中的子分类器进行验证以得到检测精度tpr和多样性div,通过这两个参数结合式(17)得到Fit,此处的α为两参数的权值,在0到1之间,在此取0.4。 Cavalcanti等人[19]选择了不合度量、Q统计量以及kappa值等多样性度量进行加权组合得到新的标准,由于模型中的决策树的多样性差异并不会太大而且更新须及时,因此本文在此只使用了不合度量(disagreement measure)计算div=(b+c)/m,它的值域在0到1之间,多样性随着该值的增大而增大,参见表1,其中b表示被hi分类为正类同时被hj分为负类的样本个数,其余依此类推,m则为总和。 Table 1 Classifier prediction result contingency table表1 分类器预测结果列联表 降序排列后留下Fit值高的一部分决策树,余下的将被剔除,并使用Buffer重训练新决策树用于补全集成模型。基于MBGSO-ARF模型自适应更新的WSN异常数据检测算法的伪代码如下所示。 算法2MBGSO-ARF(X,s,T,Buffer,data-vali,fe) 输入:数据集X;测试数据块大小s;测试样本集T;用于存储重训练决策树的样本Buffer;用于评估每棵树的小样本集data-vali;X中样本属性数fe。 1.初始化算法各参数; 2.使用RF算法训练模型rf; 3.通过MBGSO算法对rf进行优化得到剪枝后的集成模型rf-se; Whilei 4.当i 5.使用rf-se对第i块测试样本集进行检测,基于当前块更新用于存储重训练决策树的样本Buffer和小样本集data-vali; 6.对Buffer基于泊松分布随机数采样得到当前更新样本集Buffer-rebuild; 7.使用data-vali对每棵决策树的召回率以及多样性进行评估得到tpr和div; 8.以文中所选比例剔除排在最后的部分决策树,通过Buffer-rebuild重训练相应数目的决策树补全集成模型forest-new赋予rf-se; 输出:最终检测结果漏报数以及误报数。 为了评价本文所提出的异常数据检测算法的性能,使用Intel Berkeley实验室数据集和带标记的传感器网络数据集(LWSNDR)[20]完成了对比实验。实验所用PC机配置为64位Windows 7操作系统,Intel®CoreTMi7-4790 CPU,主频3.6 GHz,内存16 GB,仿真编程语言为Matlab R2014a。在相同实验环境下,分别实现了传统RF算法、MBGSO-RF算法、ARF算法以及MBGSO-ARF算法。然后,比较各自实验结果。 伯克利实验室数据集(IBRL)采集自部署于Intel Berkeley实验室中的无线传感器网络,其中包含有54个MICA2传感器节点,每个节点的数据采样周期为30 s,节点数据采集周期从2004年2月28日至2004年4月5日,节点所采集的数据包括温度、湿度、光照强度以及节点电压4个属性。本文实验中选取了9号、11号和25号传感器节点所采集的数据(表2分别记为IBRL-9、IBRL-11以及IBRL-25)。分析数据样本文件中的异常值时间戳,发现异常均为随机插入的其他不同时间段的数据样本。实验之前,首先通过时间戳将异常值标记了出来,训练数据中的标记用于作为训练标签,而测试数据中的标签则用于评价算法的性能。 另外,本文还使用LWSNDR中分别置于室内和室外的两个节点数据集(表2中记为LWSNDR-1和LWSNDR-4),属性分别对应温度和湿度,其中的异常值是人为加热水壶产生的,该数据集异常值较少。具体所取数据集如表2所示。 Table 2 Datasets of experiments表2 实验数据集 机器学习分类问题中常用的评价指标就是精度。而异常检测和分类问题的区别在于类别分布的不平衡性,异常数据和正常数据比例不相当,因此精度不适合作为异常检测的评价指标,并引出如下的评价指标。 异常检测分为两类样本:正常以及异常,研究者将训练集中占少数且拥有高识别重要性的异常样本作为正类,其余的正常样本作为负类。因此可将所检测样本根据其实际所属类别以及检测结果组成如表3所示混淆矩阵,其中有真正例(true positive,TP)、假正例(false positive,FP)、真反例(true negative,TN)、假反例(false negative,FN)。 Table 3 Confusion matrix of detection results表3 检测结果混淆矩阵 为了评价WSN异常数据检测方法的性能,本文采用召回率TPR(true positive rate)和误报率FPR(false positive rate)两个评价指标。前者也被称作查全率,是被正确检测出来的异常个数与实际为异常的样本个数的比值;后者是被算法误判为异常的正常数据样本数目与正常数据样本总数之比。由于本文算法使用了选择性集成的思想,因此增加一个评价指标:集成规模压缩比ECR(ensemble compression ratio),即最终集成规模大小ES_selective与原始集成规模大小ES_ori的比值,公式如下: 本文参数中的决策树数目的设定是根据数据实验分析得到的,GSO部分参数采用的是默认设定值,其他参数则是经过不断修改并对比实验结果采用的较优值。RF中的参数不多,包括决策树的数目m以及构造决策树时节点分裂所选属性个数fe,若数据集属性个数为d,取fe为sqrt(d)。自适应更新部分选取的size_val大小定为300,并设置每次更新剔出重训练的分类器数目为m/10,在此即为20。而GSO算法中,基本参数取值参照原文献[15]设置方法,设荧光素值挥发系数ρ为0.4,取荧光素增强系数γ为0.6,荧光素浓度Lo取5,感知半径变化率β取作0.08,种群大小Pop、移动步长Sl、最大迭代次数It_max、邻域阈值Nt、感知半径Rs以及决策半径Rd的具体取值如表4所示。 Table 4 Basic parameters in GSO表4 GSO的基本参数 萤火虫种群数目pop在此设置为和RF中决策树数目一样,3.1节中的学习因子C和最大位移Max_M则按原算法[18]设定,MBGSO算法使用的额外参数如表5所示,其中有局部变异概率阈值θ以及MBGSO中变异思想中的两个转换概率阈值P1、P2,本文使用了试凑法进行设置。 Table 5 Additional parameters in MBGSO表5 MBGSO的额外参数 本文在选取m时,分别设置为100、150以及200,并将算法用于25号节点数据进行了对比,结果如表6所示,其中Fp和Fn分别表示误报数和漏报数,可以看出m为200时,算法性能收敛基本最优,因此本文m取200。 Table 6 Algorithm performance for different values of m表6 算法在不同的m取值时的性能比较 本文在对RF进行选择性集成时对BGSO引入了变异思路,为了验证该机制对算法的有效性,依然使用了上文所选取的3个节点的数据集对MBGSO和BGSO进行了实验对比,以上2种优化算法平均耗时分别为5.43 s和4.52 s。图2和图3分别为决策树棵数设置为200和100时的对比图,从中可以看出,尽管MBGSO的迭代次数比BGSO略多几次,但前者的寻优能力要比后者更强,且收敛性更好。 Fig.3 Convergence diagram of optimization(m=100)图3 m为100时算法的寻优收敛图 因此,在后续实验里采用MBGSO算法对随机森林进行选择性集成。优化结果的对比图如图2、图3所示。 为验证本文所提算法性能,在上文所述的3个数据集上进行了实验对比,所取决策树棵树m为200,所有实验结果都是在运行30次后选取的平均值。如表7所示,带标记数据集上,由于异常不多且易于检测,检测结果基本一致,召回率均达到90%以上,不是很高的原因是测试样本中的异常数目不多。从表8可以看出,原始RF在几个数据集上的检测效果还比较理想,在检测9号和11号节点数据时的误报数目分别为1.76和0.53,该结果和选择性集成后的MBGSORF算法结果相同,但在漏报数目上高于MBGSORF,而在25号节点数据的检测效果上,原始RF算法不论是在漏报数目还是误报数目上都比MBGSO-RF算法多,说明经过选择性集成后的RF算法在检测性能方面都要优于原始RF。 接下来分成两组对比:一组是引入自适应更新模型后的ARF对比原始RF模型,另一组是未引入自适应更新的MBGSO-RF和MBGSO-ARF算法的对比,由该两组数据对比可以发现,在加入了模型更新机制后算法降低了误报数目:第1组中分别由1.76降至1.26、0.53降至0.26以及3.00降至1.80;第2组中分别由1.76降至1.20、0.53降至0.20以及3.00降至1.63。 Table 7 Detection results on dataset LWSNDR表7 LWSNDR数据集检测结果对比 Table 8 Detection results on dataset IBRL表8 伯克利实验室数据集检测结果对比 但更新机制的引入对于漏报数目的改善不是很大,由于更新模型时用于重训练决策树的样本中异常数不多,使得在新的数据环境下只是更加具备了对于正常数据样本的感知,用于重训练的样本中的异常数据的多样性不足以提供模型识别出更多的异常值。综合看平均值MBGSO-ARF算法的误报数目以及漏报数目都要少于其他3种异常检测算法,TPR均值达到99.09%。 各种算法在不同数据集上使用的模型集成大小比较如表9所示,本文MBGSO-RF算法和MBGSOARF算法在检测各数据集时所用模型集成平均大小为154.3,未优化时的模型集成大小为200,ECR为0.7718,算法实现了部分子分类器达到甚至高于原始RF性能的目的。模型集成大小降低了,因此使用MBGSO优化过的算法在检测时间上要低于优化之前的算法。 Table 9 Ensemble size of different algorithm models表9 不同算法模型集成大小 而MBGSO-RF的平均检测时间由原始RF的0.38 s降至0.33 s,MBGSO-ARF则由ARF所耗费的4.2 s降至3.23 s,具体对比如图4和图5所示。 为寻找优化收敛时间与检测结果好坏间有无关联,本文实验采用3个节点的数据,分别选取决策树个数为100、150、200进行了20次实验,以MBGSORF算法的检测结果寻找关联,时间以及误报漏报数都是3个节点数据在3种不同集成规模下的均值,具体如图6所示。 由图6可以看出,检测结果较优时优化算法的收敛时间通常较高,反之亦然,进一步表明该算法的有效性。其中2个纵轴分别表示优化所耗时间和误报漏报数目。 Fig.4 Detection time of RF and MBGSO-RF on each node图4 RF和MBGSO-RF各节点检测时间对比 Fig.6 Relationship between optimal time and Fp/Fn图6 优化时间与误报漏报数间的关系 为了凸显本文MBGSO算法相对于其他优化算法的优势,选择了使用二进制粒子群(binary particle swarm optimization,BPSO)算法对RF进行选择性集成实验,分别在伯克利数据集9号、11号和25号节点上使用MBGSO和BPSO算法对RF进行优化。对比实验中BPSO的种群大小与MBGSO设定一致,常数因子以及惯性权重分别取1.5以及0.7。对比结果如表10所示,可以看出通过MBGSO优化的子集成在检测效果上要优于后者,结果也证明了算法的有效性。MBGSO-ARF在进行WSN数据异常检测时,主要约束条件在于需要包含部分异常样本的传感器历史数据以及算法部分参数的调优,鉴于历史数据以及异常样本的获取都是可以达到的,算法参数的选取可以通过仿真实验调优。如此可见,本文算法在实际检测中是可行的。 Table 10 Detection results of 2 optimization algorithms on 3 datasets表10 两种优化算法于3种数据集的检测结果 设萤火虫种群大小为p,RF中决策树棵数为m,每次迭代选取的决策树棵数为d,数据个数为N,算法迭代次数为iter_max。首先初始化种群的时间复杂度为O(p);每次迭代在计算所选组合的适应度函数值时的时间复杂度为O(p×d);每次迭代计算萤火虫个体荧光素更新以及之间距离的时间复杂度分别为O(p)和O(p2×m);个体位置和决策域半径更新过程的时间复杂度分别为O(p×m)和O(p);每次迭代进行变异过程的时间复杂度为O(p×m)。因此MBGSO算法时间复杂度为O(iter_max×p2×m)。 假设有n个训练样本,T个测试数据,特征数fe,单位数据块大小为s_block,Buffer大小s_buf,小样本验证集大小为s_val,CART算法时间复杂度为O(fe×n(lgn)),RF在构建时选取特征mtry小于fe且不剪枝,因此RF时间复杂度为O(m×mtry×n(lgn))。而计算当前决策树Fit值的时间复杂度为O(m×s_Val),重训练时间复杂度为O((m/10×mtry×s_buf×lg(s_buf)))。因此复杂度为O(T/s_block(m/10×mtry×s_buf×lg(s_buf))+m×mtry×n(lgn))。从实验结果可以看出,优化后的模型集成大小降低了近30%,MBGSO-ARF所耗时间由ARF的4.2 s降至3.23 s,若优化后集成大小为L,优化后检测复杂度为O(L(fe×T×lgT))对应了后者3.23 s,而原始检测复杂度为O(m(fe×T×lgT))则对应了前者4.2 s,这部分时间的节约即对应了使用子集成检测与原始集成检测时间的差值。 本文算法使用MBGSO优化随机森林,选择了最优子集成并引入模型更新机制,在提高检测算法的召回率,并降低误报率的前提下,缩小了所使用的模型集成大小,节省了检测所耗时间,提高了异常检测的效率。 本文结合RF和选择性集成思路提出了一种无线传感器网络异常数据检测算法(MBGSO-ARF)。该方法在二进制萤火虫算法的基础上加入了变异思路,避免了算法出现过早收敛的情况,使其在对RF选择性集成时获得更优的解,并以子集成模型结合自适应更新模块对待测样本进行异常检测,克服了使用单一的RF训练模型执行检测的缺点,实时地对部分子分类器进行重新训练并加入集成模型中,使得模型一定程度上能更适应当前数据。实验结果表明MBGSO-ARF算法的效率和异常数据检测的准确性都有了提高。由于MBGSO-ARF算法采用固定的模型更新方式,今后考虑在模型更新的约束条件等方面进行改进,以进一步提高算法的性能。3.2 WSN数据异常检测与模型自适应更新
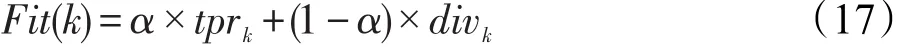
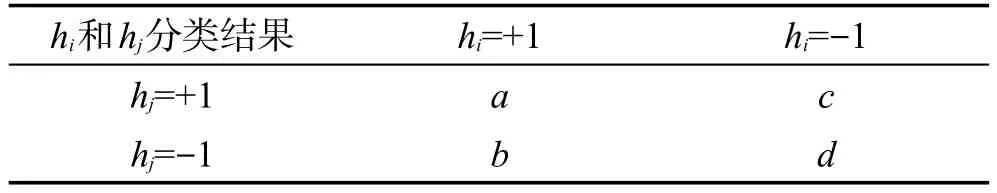
4 仿真实验
4.1 数据集介绍
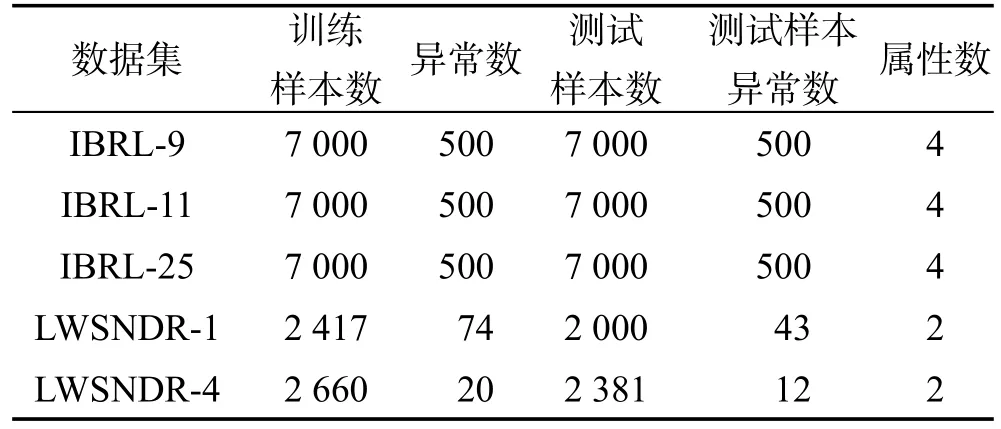
4.2 算法性能评价指标


4.3 实验参数设置


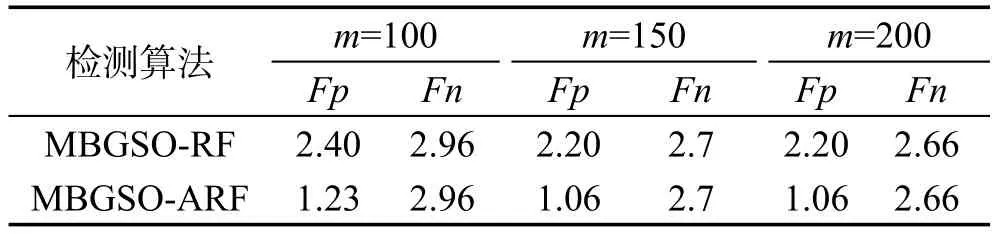
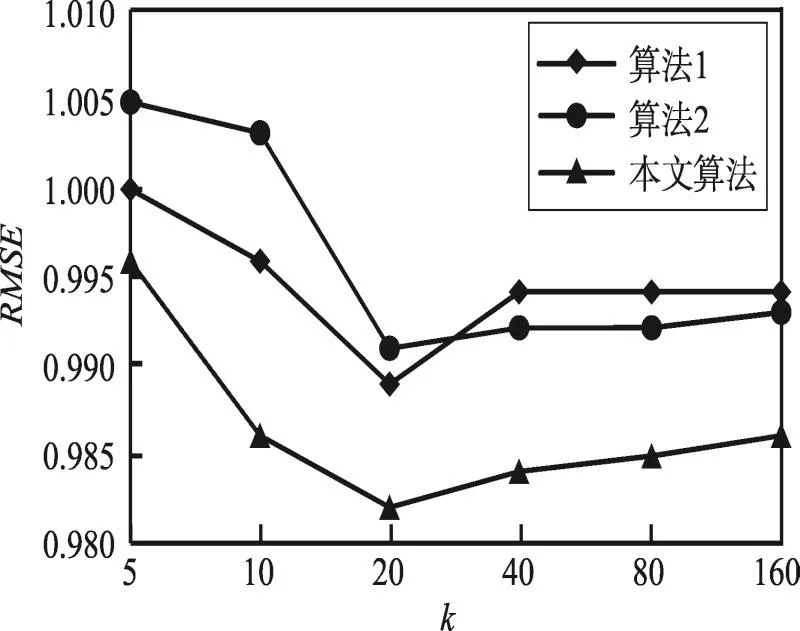
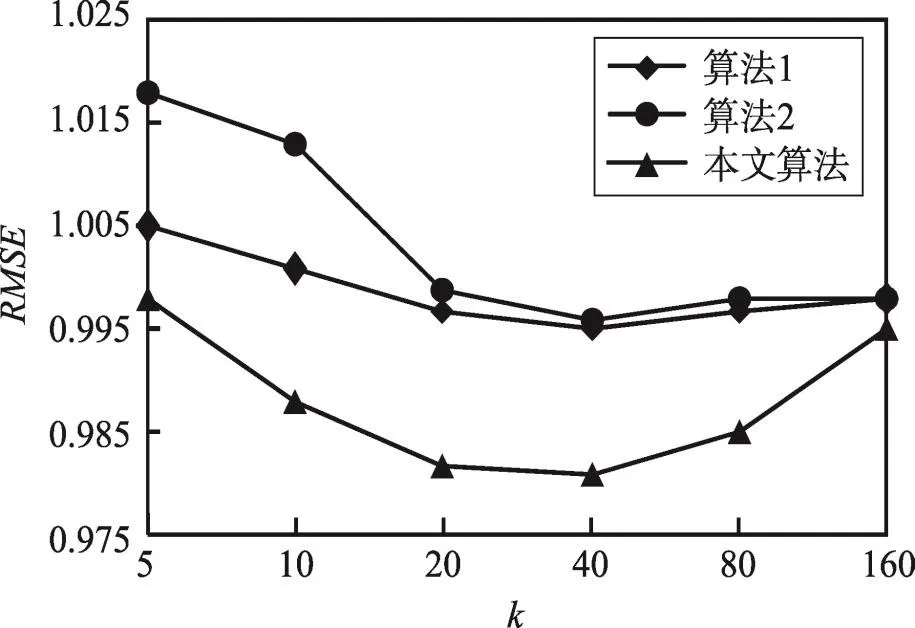
4.4 MBGSO与原始BGSO优化结果对比
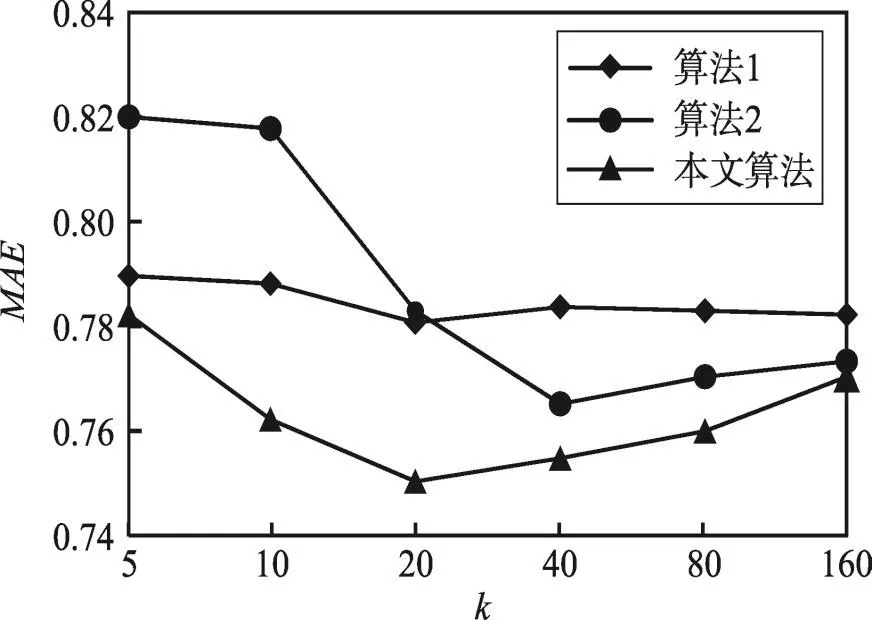
4.5 异常检测算法对比实验


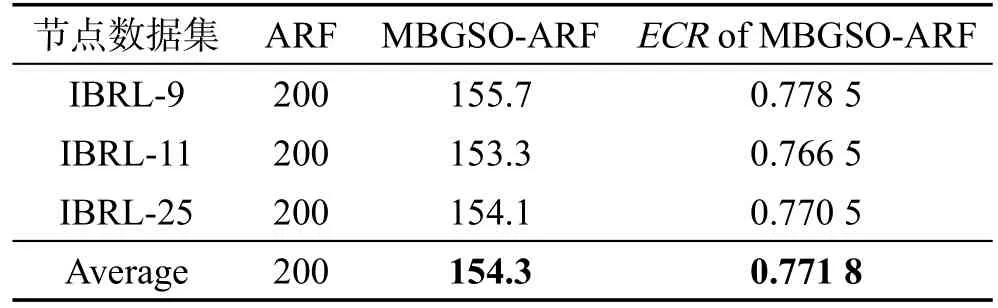
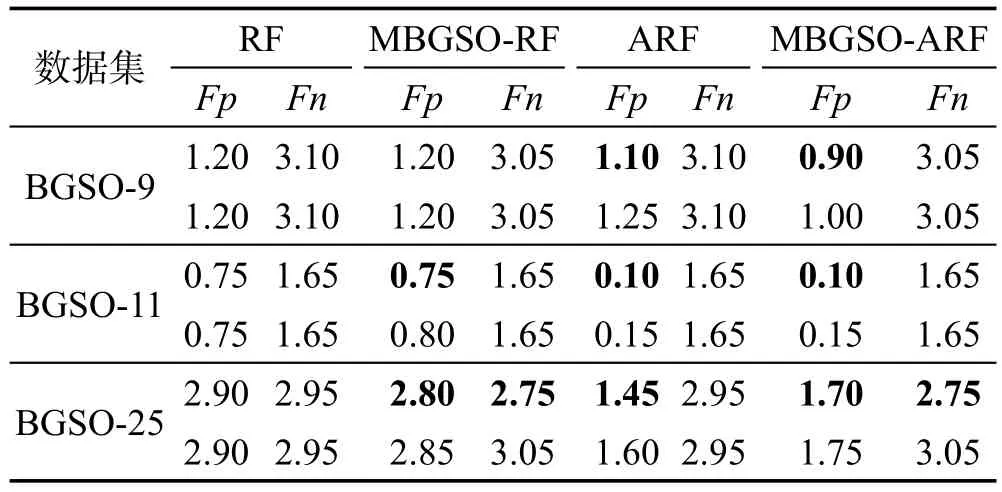
4.6 算法复杂度分析
5 结束语
