并发加权μ-演算的若干性质*
2018-10-12余寒
余 寒
南京航空航天大学 计算机科学与技术学院,南京 211106
1 引言
在模型检测领域,时间自动机[1]、加权自动机[2]和加权时间自动机[3]用于建模和分析数量层面的系统性质。进程代数用来模拟模块化的性质,但它无法表达基本布尔操作符,达不到系统规范[4]要求。像空间逻辑[5-6]、分离逻辑[7-8]、概率逻辑[9]这类模块化逻辑对于处理并发非确定性系统很有效,但在反映系统数量层面的各种性质上还有欠缺。
为了集中处理这些问题,Larsen等人提出了并发加权逻辑[10](concurrent weighted logic,CWL),这种多模态的逻辑中包含了反映给定状态的资源总量和限制转移过程的模态词,以及能够应对组合性系统的二元模态词,它可以表达标记加权转移系统(label weighted transition system,LWS)的质化、量化和模块化的性质。基于此,本文将不动点算子加入CWL,扩充后得到并发加权μ-演算(concurrentweightedμ-calculus,CWC),并给出了轮替树自动机[11-12]与CWC间的内在联系,借此证明了CWC的可判定性、小模型性。
本文组织结构如下:第2章介绍相关术语以及LWS;第3章提出CWC并给出其在LWS上的语义解释;第4章引入轮替树自动机,并阐述了轮替树自动机与CWC公式间的内在联系;第5章根据第4章的研究得出CWC的相关性质;第6章总结全文。
2 预备知识
本文采用如下一些记号:ℝ表示实数集合;ℚ表示有理数集合;采用集合论方式定义自然数,令n为任意自然数,则n={0,1,…,n-1},ω表示自然数集合;Q={p,q,r…}表示命题变元的集合;M×S表示集合M和集合S的笛卡尔积;|S|表示集合S的基数;|ϕ|表示公式ϕ的子公式集合的大小。
集合M上的有限序列是函数n→M,其中n为一个自然数;集合M上的无限序列是函数ω→M;一个序列π是有限序列或者无限序列,其长度记作|π|。树是一个二元组 (V,E),V是节点的集合,E是V×V的子集。树中任意节点v∈V的后继节点的集合记作Scc(v),如果树中某节点v∈V满足Scc(v)=∅,则该节点称为死点。
树T=(V,E)上的一条路径是V上的一个序列π,该序列满足如下条件:对于任意的i+1< |π|,(π(i),π(i+1))∈E。树T的一个分支是从根节点开始的最大的路径,则一个分支是始于根节点终于某死点的有限路径或者是始于根节点的无限路径。T↓v表示以v为根节点T的子树。
定义1[10,13](标记加权转移系统)LWS是一个五元组W=(M,Σ,θ,l,ρ),其中:
(1)M是一个非空的状态集。
(2)Σ是一个非空动作集。
(3)θ:M×(Σ×ℝ)→2M是一个状态转移函数。
(4)l:M→ℝ是一个满足下列条件的函数:如果m′∈θ(m,a,x),则l(m′)=l(m)+x。一般称函数状态l为标记函数。
(5)ρ:Q→2M是一个解释函数。对于p∈Q,N⊆M,解释函数ρ[p↦N]满足下列条件:如果p′=p,则ρ[p↦N](p′)=N;如 果p′≠p,则ρ[p↦N](p′)=ρ(p′)。
对于任意LWSW=(M,Σ,θ,l,ρ),p∈Q,N⊆M,W[p↦N]表示这样的标记加权转移系统:W[p↦N]=(M,Σ,θ,l,ρ[p↦N])。而定点标记加权转移系统是一个二元组(W,m),其中W是LWS,m是W中的一个状态,称作定点标记加权转移系统的标识状态。对于一个定点标记加权转移系统(W,m),W↓m表示限制在状态m上的W 的子模型。令W1和W2为任意 LWS,W1⊎ W2表示 W1和 W2做不相交的并所得模型。
定义2[10,14](加权互模拟)给定一个LWSW=(M,Σ,θ,l,ρ),一个加权互模拟是一个等价关系R⊆M×M,使得对于任意(m,m′)∈R,如下条件成立:
(1)l(m)=l(m′);
(4)对于任意q∈Q,m∈ρ(q)当且仅当m′∈ρ(q)。
如果存在一个加权互模拟关系R使得(m,m′)∈R,则称m和m′是互模拟的,记作m∼m′。可以将此定义扩展为不同LWSs间的加权互模拟:若Wi=(Mi,Σi,θi,li,ρi),mi∈Mi,i=0,1且m0和m1互模拟,则 (W0,m0)∼(W1,m1)。
定义3[10](LWS乘积)给定一个同步函数[15]∗:Σ×Σ→Σ以及两个 LWSWi=(Mi,Σi,θi,li,ρi),i=0,1 。 W=(M,Σ,θ,l,ρ)是 W0和 W1的乘积,记作 W=W0⊗W1,其中:
(1)M=M0×M1。
(2)Σ=Σ0∗Σ1={a0∗a1|a0∈Σ0,a1∈Σ1}。
(3)l:M→ℝ是满足下列条件的函数:如果(m0,m1)∈M,则l((m0,m1))=l0(m0)+l1(m1)。
(4)θ:M×(Σ×ℝ)→2M是满足下列条件的函数:如果 (m0,m1)∈M,a∈Σ,并且x∈ ℝ,则θ(m,a,x)={(m0′,
(5)ρ:Q→2M是满足下列条件的函数:如果q∈Q,则ρ(q)={(m0,m1)∈M|m0∈ρ0(q),m1∈ρ1(q)}。
易证W0⊗W1是LWS。
例1图1中展 示的是 LWSW1和 W2和其乘积W0⊗W1。假设a*c,a*d,b*c在同步函数中已有合法定义(b*d不合法)。状态(m0,n0)的实数标记是m0和n0的实数标记之和。m0经动作a转移到m2,n0经动作c转移到n1,而a*c是转移过程的同步,故(m0,n0)到(m2,n1)的转移带动作标记a*c,并且带实数标记2,此实数标记是两个子转移过程的代价之和。p在m0,m1上成立,q在m0,n0上成立,r在m2,n0上成立,则在W0⊗W1中,q在(m0,n0)上成立。
Fig.1 LWSs and their products图1 LWS和其乘积
3 并发加权 μ-演算
CWC能够反映LWS的特点,并包含了不动点算子,相较CWL具有更强的表达能力。
定义4(基本公式)CWC的公式由以下BNF范式定义:
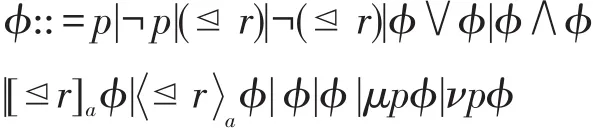
其中r∈ℚ,a∈Σ,p∈Q,⊴∈{≤,≥}。在形如μpϕ、νpϕ这样的公式中,要求变元p在ϕ中正出现(也即,¬p不出现)。
Fμ指以μ开头的不动点公式集合,Fν则是以ν开头的不动点公式集合。Fη是不动点公式集合,由Fμ和Fν组成。在CWC公式中,不动点操作符优先级高于组合模态词“|”,组合模态词优先级高于一元模态词 [⊴r]a,⊴ra。当一个CWC公式ϕ中的每个命题变元p最多只被限制一次并且每个p在其限制量词的辖域内,则ϕ是范式形式。对于一个出现在范式形式CWC公式ϕ中的受限变元p,ϕ的唯一的子公式ηpφ(η∈{μ,ν})记作ϕp。显然,每个CWC公式可以通过在必要时重命名受限变元形成等价的范式形式。下文中的CWC公式均指其范式形式。
将CWC公式在LWS上进行解释,对于给定LWS W=(M,Σ,θ,l,ρ)和CWC公式ϕ,集合 ||ϕ||W⊆M按归纳方式定义,见图2。

Fig.2 LWS semantics of CWC图2 CWC的LWS语义解释
例2对于公式ϕ=μq(p|(≥ 2)∨[≤ 5]aq),在LWS W 中,||ϕ||W表示这样的状态的集合,从该状态出发,在有限步内(可能是0步),可以到达一个使得公式p|(≥2)成立的状态。
能够满足公式ϕ的定点标记加权转移系统集合,记作||ϕ||,则:
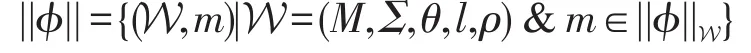
对于每一个CWC上的模态操作符及不动点操作符,其在||ϕ||上的相关操作见图3。
首先对于连接符,易知,对于任意CWC公式φ、ψ:
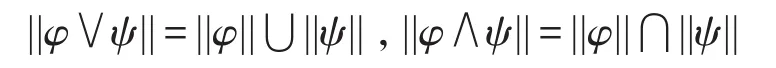
另外,据图3易知,对于任意CWC公式φ、ψ:
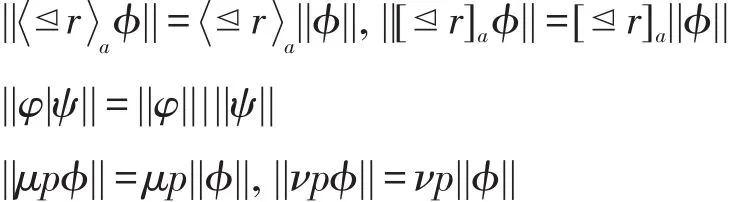
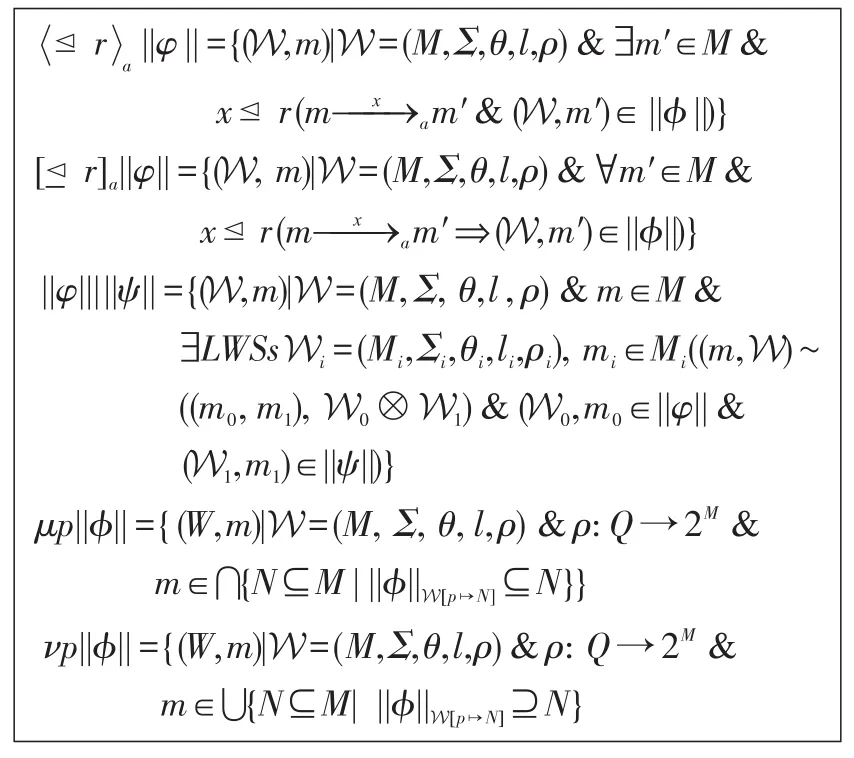
Fig.3 Some operations on||ϕ||图3 ||ϕ||上相关操作
4 轮替树自动机与CWC的联系
定义5[12](轮替树自动机)轮替树自动机是一个四元组 A=(S,s0,δ,Ω),其中:
(1)S是一个有限的状态集合。
(2)s0∈S是一个初始状态。
(3)Ω:S→ω是一个优先级函数,为每个状态指派一个自然数优先级标记。
(4)δ:S→TC是转移函数,将每个状态映射到集合TC上,集合TC是满足下列条件的最小的集合:0,1 ∈TC;如果r∈ ℚ ,则r∈ ℚ,(⊴r),¬(⊴r)∈TC;如果q∈Q,则q,¬q∈TC;如果s∈S,则s,⊴ras,[⊴r]as∈TC;如果s,s′∈S,则s∧s′,s∧s′,s|s′∈TC。
轮替树自动机的计算行为用执行(run)[12]的概念来解释。令 A=(S,s0,δ,Ω)为一个轮替树自动机,(W,m0)是个定点标记加权转移系统,其中W=(M,Σ,θ,l,ρ)。 A在(W,m0)上的一次执行是树R=(V,E,λ),其中(V,E)是定义树的二元组,而λ:V→M×S是一个双标记函数。该树的根节点标记为(m0,s0),并且每个带有双标记(m,s)的节点v满足下列条件:
(1)δ(s)≠ 0 。
(2)如果δ(s)=q,则m∈ρ(q);如果δ(s)≠q,则m∉ρ(q)。
(3)如果δ(s)=(⊴r),则l(m)⊴r;如果δ(s)= ¬(⊴r),则l(m)⋬r。
(4)如果δ(s)=s′,则存在v′∈Scc(v),使得λ(v′)=(m,s′)。
(5)如果δ(s)= ⊴ras,则存在v′∈Scc(v),m′∈M并且使得λ(v′)=(m′,s′)。
(6)如果δ(s)=[⊴r]as,则对于所有x⊴r,存在v′∈Scc(v),使得λ(v′)=(m′,s′)。
(7)如 果δ(s)=s′∨s″,则 存 在v′∈Scc(v) 使 得λ(v′)=(m,s′)或者λ(v″)=(m,s″)。
(8)如果δ(s)=s′∧s″,则存在v′,v″∈Scc(v)使得λ(v′)=(m,s′)并且λ(v″)=(m,s″)。
(9)如果δ(s)=s′|s″,则存在v′,v″∈Scc(v)和m′,m″∈M使得λ(v′)=(m′,s′)并且λ(v″)=(m″,s″)。
当一次执行R的每一个无限分支上的状态优先级标记满足由Ω确定的奇偶接收条件,这个执行R能够被接收。确切地说,对于每一个R的无限分支π,将优先级函数Ω应用到每个节点上,对于所得到的自然数序列,当其中无限次出现的最大自然数是偶数,这个分支能够被接收。如果R的每个无限分支是可接收的,则R是可接收的。
当一个定点标记加权转移系统上存在一个关于A可接收的执行,则这个系统是能够被A接收的。能够被A接收的语言,记作||A||,它包含了所有能够被A接收的定点标记加权转移系统。
接下来为每个CWC公式构建一个轮替树自动机用以接收此公式定义的定点标记加权转移系统。这种从CWC到轮替树自动机的翻译过程容易创建,关键是其正确性的证明。
令ϕ为一个CWC公式,轮替树自动机A(ϕ)=(S,s0,δ,Ω),其中:
(1)S是个包含ϕ的所有子公式φ(记作φ)的集合。
(2)s0=ϕ是初始状态。
(3)δ是转移函数,具体定义见图4。
(4)Ω是优先级函数,定义方式同文献[16]。

Fig.4 Definition of transform functionδ图4 转移函数δ定义
例3对于例2公式ϕ=μq(p|(≥ 2)∨[≤ 5]aq),构建其轮替树自动机 A(ϕ),初始状态为μq(p|(≥2)∨[≤5]aq),转移函数如下:
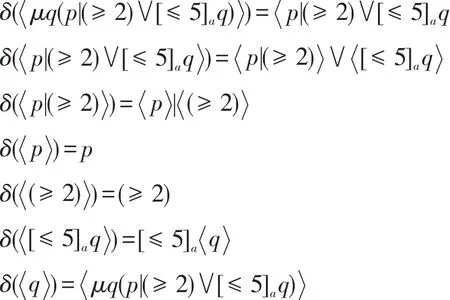
按照文献[16]中优先级定义方式,除了状态μq(r∨ [≤ 3]aq|(≤ 5)的优先级为1,其余状态优先级均为0。
下面证明几个定理,用以说明CWC的操作符和连接词是如何用自动机来建模的。
定理1[12]令A和A′为两个轮替树自动机,则:
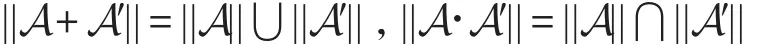
定理2[12]令A为一个轮替树自动机,则:
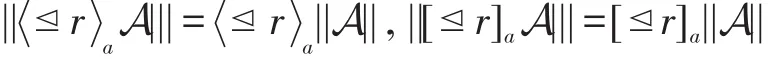
定理3[12]令p为命题变元,A是轮替树自动机,则:
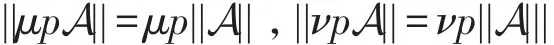
定理1~3中涉及的自动机 A+A′,A∙A′和 ⊴raA(φ),[⊴r]aA(φ)以及μpA,νpA的定义见文献[12]。
定义6令A和A′为两个轮替树自动机,s0为某个新的状态,则A|A′定义为:
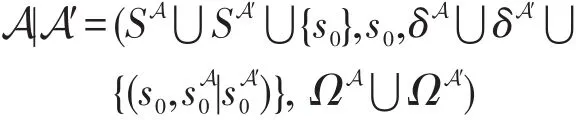
令φ和ψ为CWC公式,则容易看出A(φ|ψ)=A(φ)|A(ψ)。
基于定义6,可以得到定理4。
定理4令A和A′为两个轮替树自动机,则:
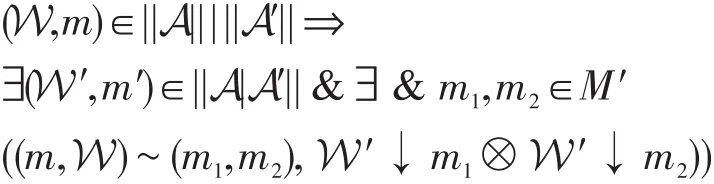
其中,M′是W′的状态集,另一方面:

其中,M是W的状态集。
证明对于任意两个自动机A和A′,令A=(SA,首先证明本定理第一部分,假设 (W,m)∈ ||A|||||A′||,则存在 LWSs Wi=(Mi,Σi,θi,li,ρi),mi∈Mi,i=1,2使得 (W,m)∼ (W1⊗ W2,(m1,m2))并且以下条件成立:(W1,m1)∈||A||,(W2,m2)∈||A′||。令R1为A在(W1,m1)上的一次可接收执行,R2为A′在(W2,m2)上的一次可接收执行。考虑这样的树,它的根节点标记为(m,s0)(s0为某个新状态)且恰有两个后继v1和v2,以v1为根节点的子树与R1相同,以v2为根节点的子树与R2相同,则这棵树是 A|A′在(W⊎W1⊎W2,m)上的可接收执行。此时,(W⊎W1⊎W2,m)∈ ||A|A′||。
接着证明本定理第二部分。假设(W,m)∈||A|A′||,则A|A′在(W,m)上存在一个可接收执行R,且R的根节点有且仅有两个后继节点v1和v2,标记分别为。显然,R↓v1和R↓v2分别是A和 A′在定点标记加权转移系统(W↓m1,m1),(W↓m2,m2)上的可接收执行。那么(W↓m1,m1)∈||A||且 (W↓m2,m2)∈ A′。令 (W′,m′)=(W↓m1⊗ W↓m2,(m1,m2)),则有 (W′,m′)∈ ||A|||||A′||。 □
当 |A||||A′||与 ||A|||||A′||间具有定理 4 所述关系,则||A|A′||≅ ||A|||||A′||,称二者互模拟等价。
这一章主要的定理是正确性的证明,即满足ϕ的定点标记加权转移系统与自动机 A(ϕ)能接收的语言是互模拟等价的。
定理5令ϕ为任意CWC公式,则当ϕ中包含模态词 |时,||ϕ||≅ ||A(ϕ)||,否则 ||ϕ||=||A(ϕ)||。
证明按照公式ϕ的复杂度归纳证明。当ϕ为p,¬p,(⊴r),¬(⊴r)时,显然 ||ϕ||=||A(ϕ)||成立。否则分情况讨论,若ϕ的最外层连接词是析取和合取,定理1说明此情况成立;若最外层操作符是一元模态词[⊴r]a和 ⊴ra,定理2说明此情况成立;若最外层操作符是不动点操作符,定理3说明此情况成立;若最外层操作符是二元模态词|,定理4说明此情况成立。□
5 相关结论
5.1 可判定性
有了上一章的等价性,关于CWC的可满足性判定可归结到自动机的非空问题上。
定理6[12,16]轮替树自动机的非空问题在指数时间内可判定。
根据定理5和定理6可直接得出定理7。
定理7CWC的可满足性问题在指数时间内可判定。
5.2 小模型性
CWC的小模型性也可以利用上一章的等价性来证明。
定理8[17]如果一个轮替树自动机A=(S,s0,δ,Ω)所接收的语言非空,那么它可以接收一个状态集不超过2Ο(|S|4lg|S|)的定点标记加权转移系统。
定理9一个CWC公式ϕ能够被某些定点标记加权转移系统满足,则存在一个状态集不超过2Ο(|ϕ|4lg|ϕ|)的定点标记加权转移系统满足它。
证明根据定理5和定理8可知,对于一个CWC公式ϕ,如果 A(ϕ)=(S,s0,δ,Ω)所接收的语言非空,那么它可以接收一个状态集不超过2Ο(|S|4lg|S|)的定点标记加权转移系统,由A(ϕ)的构造过程可知,该定点标记加权转移系统的状态集不超过 2Ο(|ϕ|4lg|ϕ|)。根据定理 5可知,若公式ϕ中不包含组合模态词 |,则存在一个状态集不超过 2Ο(|ϕ|4lg|ϕ|)的定点标记加权转移系统满足它。否则,根据定理4,令L(ϕ)表示公式ϕ的长度,可得到结论,存在一个状态集不超过 (2Ο(|ϕ|4lg|ϕ|))L(ϕ)(i.e.2Ο(|ϕ|4lg|ϕ|))的定点标记加权转移系统满足ϕ。 □
6 结束语
本文在CWL的基础上,提出了CWC,给出了它在LWS上的语义,并阐述了轮替树自动机与CWC之间内在的联系。这种联系在探讨CWC的可满足性及小模型性等问题上起到重要作用。而如何使用轮替树自动机探索CWC的公理系统,验证其可靠性和完备性还有待进一步研究。
