融入项目相关性的加权Slope One算法研究*
2018-10-12徐红艳王嵘冰
冯 勇,徐红艳,王嵘冰,郭 浩
辽宁大学 信息学院,沈阳 110036
1 引言
信息技术和网络互连的快速发展,带来信息量的激增,人们正步入信息过载的时代[1]。目前,个性化推荐技术被业界认为是解决信息过载问题的首选方案,它根据使用者的历史交互数据开展数据的分析与挖掘,将用户可能感兴趣而又未获取的产品、信息等推荐给用户[2]。近年来,个性化推荐技术已经被广泛应用在电影、视频、论文、驾驶路线和位置等与信息相关的服务领域。
目前,众多的个性化推荐方法中,协同过滤推荐是应用较为成功的推荐方法,分为基于用户的协同过滤推荐和基于项目的协同过滤推荐[3]。Slope One算法作为应用广泛的基于项目的协同过滤推荐算法,是由Lemire等人于2005年提出的。该算法易于实现,推荐准确度较高[4]。但该算法在实现时,将所有项目平等对待,未对项目的相关性加以考量,并且在数据集稀疏时推荐效果不佳。文献[4]中同时也提到了加权Slope One算法,该算法将同时被评分的两个项目的用户数量作为加权值,但是同样缺乏对项目相关性的考量,推荐效果不甚理想。针对Slope One算法的不足,众多学者从不同视角进行了改进,如:Xiao等人将Slope One算法与基于内容的推荐算法相结合,但此算法在数据稀疏时的推荐效果不理想[5]。Wang等人提出将机器学习的相关算法应用于Slope One算法参数的学习计算中,再预测推荐[6]。孙丽梅等人提出了基于动态k近邻的Slope One算法,采用用户相似度的k近邻方法筛选用户评分数据,提高了推荐准确性[7]。但是,上述方法均没有从项目类型上入手,减少无关项目对预测结果的不良影响。因此,本文在传统Slope One算法中加入了项目类型相关性计算及项目筛选策略,提出了一种融入项目相关性的加权Slope One算法,使算法的推荐效率和推荐准确率均得到了一定程度的改善。最后经实验对比分析,本文所提算法切实可行,与当前应用较广的Slope One算法相比具有更优的推荐效率和准确率。
2 相关工作
2.1 Slope One算法介绍及不足分析
Slope One算法本质上是基于项目的协同过滤推荐算法,该算法认为在项目和项目之间、评分和用户自身之间存在着一种线性关系。Slope One算法是采用公式f(x)=x+b来预测评分的。b代表着项目间的平均评分偏差,x表示评分值。
假设S={

计算出评分差估计值b后,采用如上所提的线性关系,根据目标用户给出的项目X的评分和b来对项目Y的预测评分进行估算。
Slope One算法对预测评分计算的一般流程如下:
(1)生成用户集合U:在用户-项目评分矩阵中,将所有对目标项目做过评分的用户筛选出来形成用户集合U。
(2)生成项目集合P:首先找出已被目标用户给出评分的项目,若该项目也同时被其他用户给出评分,则该项目将被加入到算法计算所需的项目集合P中。
(3)预测项目评分[8]:筛选出U、P之后,就可以提取Slope One算法需要的评分数据,即U与P交叉处的评分数据。多项目条件下,用户u预测项目j的评分表示为P(u)j,计算公式如式(2)、式(3)所示:
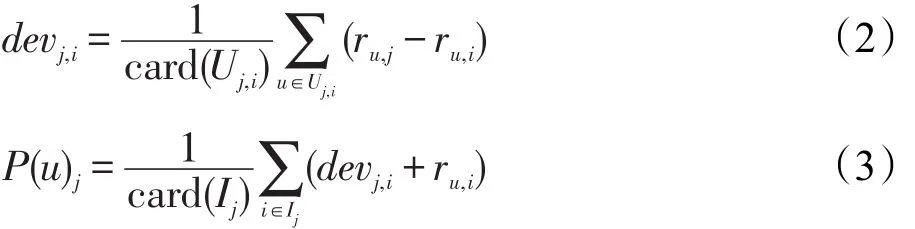
其中,devj,i表示项目j相对项目i的评分偏差;Uj,i表示项目i和项目j有共同评分的用户集合;ru,i和ru,j分别表示用户u对项目i、j的评分;Ij表示与目标项目j同时被评分的项目集合;card()表示相应集合中包含元素的数量。
Slope One同其他推荐算法一样,在预测完项目评分之后采用Top-N方式生成推荐列表。
通过对Slope One算法计算方式的分析,可总结出该算法有如下两点不足:
(1)该算法仅仅考虑了当前用户的评分项目与目标项目之间的平均评分偏差,再求加权平均值计算得出。由于没有考虑项目间的相关性,因此算法在对预测评分进行计算过程中,极有可能将与目标项目在性质上完全不相关的项目纳入项目集合中,计算结果就会有较大的偏差。
(2)文献[9-10]研究的结果表明,该算法在数据集较为稠密时,预测精度较高,但当数据集相对稀疏时,该算法在推荐效果上的优势并不明显。
基于上述两种不足导致该算法推荐的结果准确度不理想,本文算法将围绕以上两方面的不足开展研究与改进工作。
2.2 项目相似度计算方法介绍及不足分析
目前对项目相似度的研究大多集中在项目评分上的相似度或项目的评价信息作为切入点来计算相似度,而没有从项目类型等项目本质信息来衡量。目前常用的项目相似度计算方法及不足分析如下:
(1)根据购买次数计算
两个不同项目被同一用户购买的次数越多,它们就越相似[11]。项目j和项目i之间的相似度计算如式(4)所示:

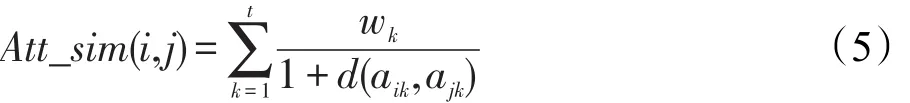
这种方法在计算属性相似度的时候,计算过程非常繁琐。
(3)多层次计算
此方法首先基于共同用户集计算第1级相似度,然后逐步融入其他维度因素[13],计算过程如下:
基于共同用户集的第1级相似度计算。设项目i、j的用户集分别为Usr(i)、Usr(j),则使用式(6)计算项目i、项目j的相似度:
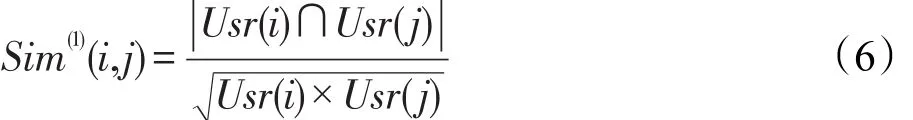
其中,Ti表示项目i总共被购买的次数;Tj表示项目j总共被购买的次数;Ti∪Tj表示项目i和项目j被同一用户购买的次数。这种方法带有一定的偶然性,不适合用在预测评分的系统中。
(2)根据项目属性
在该计算方法中,项目之间的相似度使用项目属性相似度来衡量[12]。项目有很多属性,因此每个项目可以表示为一个t维向量,每个维度对应当前项目的一个属性特征。aig表示项目i的第g个属性,利用相关公式确定每个属性在最终推荐中所占不同的权重wk,然后加权得到两个项目属性的相似度。那么项目i和项目j之间的相似度可以表示为式(5):
融入活跃度的第2级相似度计算。用户u的活跃度通过其评分项目数量RNum(u)来表示,则第2级相似度计算如式(7):
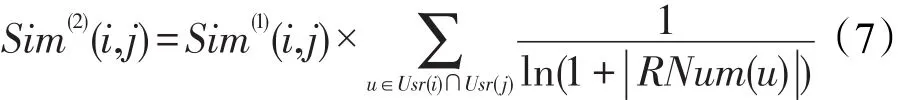
融入时效的第3级相似度计算。设用户u对项目i和项目j的评分时间分别为Timeui和Timeuj,则第3级相似度计算如式(8):
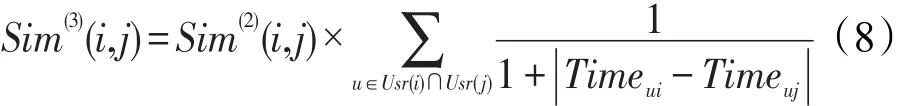
以上给出的多级相似度计算虽然能够从不同角度分析项目之间的相似性,但是算法的实现过程中需要进行大量的计算,并且算法效率较传统算法并没有较大提高,其时间复杂度为O(mlgm),m为全部项目数。
3 融入项目相关性的加权Slope One算法
针对Slope One算法中存在的不足,本文提出了项目相关性的计算方法,从项目类型上入手,减少无关项目对预测结果的影响。结合Slope One算法计算平均评分差值的特点,对用户-项目矩阵进行筛选操作,目的是得到一个局部数据稠密的用户-项目矩阵,并且项目间评分差值较为稳定。最后将项目类型相关性计算和项目筛选策略融合到推荐算法中,形成融入项目类型相关性的加权Slope One算法。
3.1 项目相关性的计算
该步骤是进行数据预处理的过程,根据项目数据集的相关数据计算出项目之间的相关性,得到一个类型相关性的表格,然后就可以根据计算结果和目标项目的类型进行筛选。这样既可以过滤掉无关项目的干扰,又可以减少用户-项目矩阵的局部相似度。
3.1.1 项目相关性的定义
本文提出的计算方法是利用项目已有的相关数据来计算项目之间的相关性。项目类型a和b之间的相关性表示为g_corr(a,b),计算如式(9)所示:
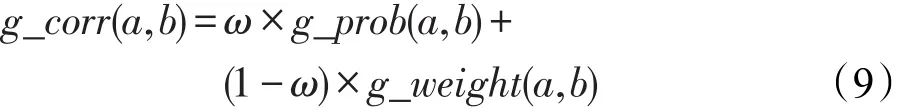
在式(9)中,项目类型之间的相关性g_corr(a,b)是由g_prob(a,b)和g_weight(a,b)来计算。项目类型共同出现的概率矩阵表示为g_prob(a,b),这个概率矩阵是不对称的。项目类型评分相似度矩阵表示为g_weight(a,b),是由皮尔逊相关系数计算的一个对称矩阵。ω表示两者权重,由反复实验得到最优取值。
3.1.2 项目类型共同出现概率的计算
在推荐系统的项目数据中,每个项目都至少有一个所属类型,有些项目甚至有4到5个所属类型。比如电影数据中,《海豚湾》的所属类型为纪录片,而《拯救大兵瑞恩》属于剧情片、动作片、历史片和战争片。
在兴趣相似度中,如果两个用户共同感兴趣的物品越多,则说明这两个用户的相似度越高。借鉴该思想,如果两个类型同时被一个项目所属的情况数量很多,那么可以认为这两个类型是有一定关系的,即相关度高。本文就是根据这种思想来衡量两个项目类型是否具有关系。在本文提出的计算方法里,项目类型共同出现的概率用条件概率来计算,计算公式如式(10):
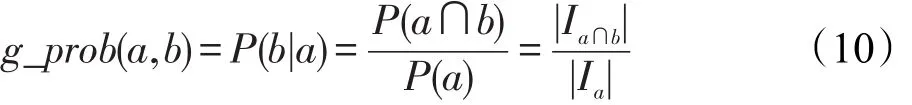
式(10)中Ia表示项目类型属于类型a,Ia∩b表示项目类型既属于类型a又属于类型b。例如:A影片属于类型 1、2、3,B 影片属于类型 3、4、5,则g_prob(a,b)=1/3。
3.1.3 项目类型评分相似度计算
类型权重公式如式(11)所示,这是一个皮尔逊相关系数的变形,用来计算属于类型a和类型b项目评分之间的评分相关性。
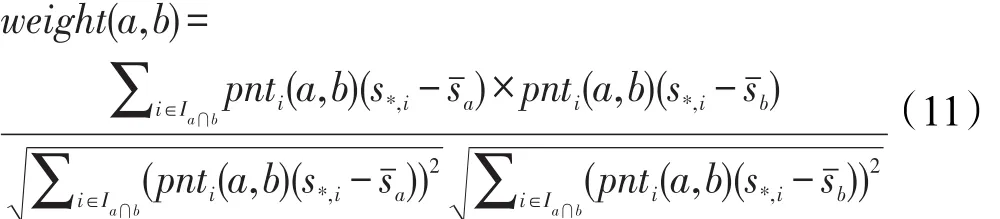
其中,pnti(a,b)表示项目i的点数;s*,i表示项目i的平均得分;sˉa和sˉb表示类型为a和类型为b的项目的平均分。
正如前面所说,一个项目可以对应很多类型。一个项目对应的类型越少,对应类型间的相关性越高。因此,pnti是根据一个项目所属类型的总数不同来给定的。计算公式如式(12)所示。

其中,类型权重等式有两个目标类型,pnti计算公式中的分子是2,Gi表示项目i所属类型的集合,|Gi|是项目i所属的类型的总数。
3.2 项目的筛选策略
本文以用户-项目矩阵中的评分数据为基础,利用项目固有的类型信息,提出以下项目类型筛选策略用以挖掘出用户最喜欢和最不喜欢的项目作为算法预测评分过程中参与计算的项目。
项目的类型集合G={g1,g2,…,gn}。当Rui=5时,认为用户u喜欢项目i。此时,项目i对应的项目类型gc被标记为用户u的喜欢项目类型。某个用户可能多次对同一个喜欢的项目类型进行标记,对标记次数进行累加,形成用户喜欢的项目矩阵。同理,当Ruj=1时,认为用户u不喜欢项目j。此时,项目j对应的项目类型gd被标记为用户u的不喜欢项目类型。对标记次数进行累加,形成用户不喜欢的项目矩阵。
表1中列出了用户u1至u5对项目i1至i7的评分矩阵。将其分开表示成两个矩阵,一个为保留用户评分为5的,一个为保留用户评分为1的,同时将其他评分值重置为0,操作结果如表2和表3所示。
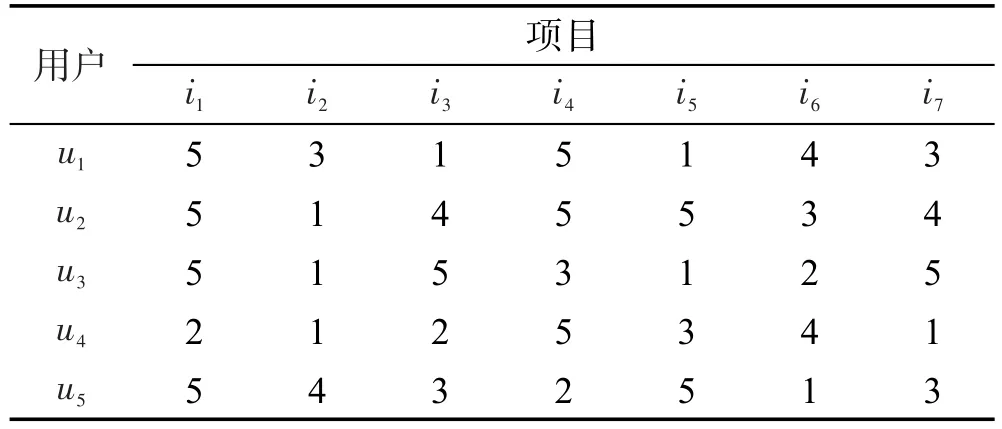
Table 1 User-item scoring matrix表1 用户-项目评分矩阵
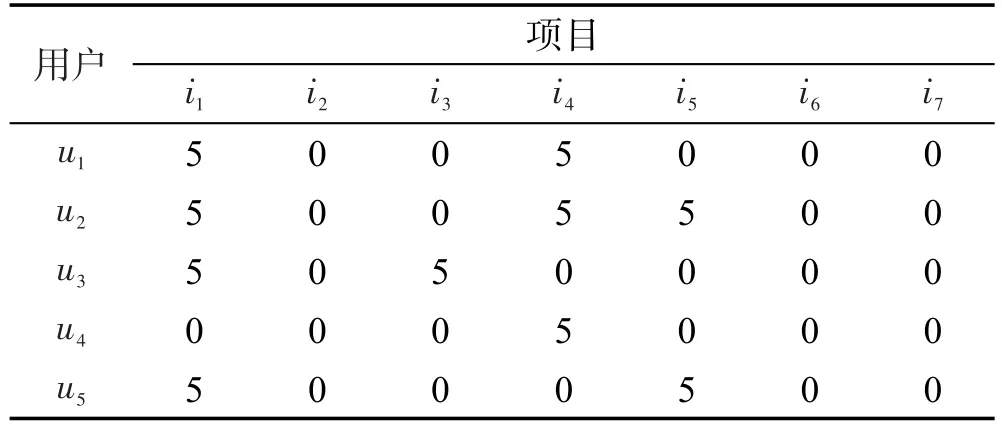
Table 2 User favorite item matrix表2 用户喜欢的项目矩阵
项目-类型矩阵如表4所示,项目i属于类型g就记为1,否则记为0。
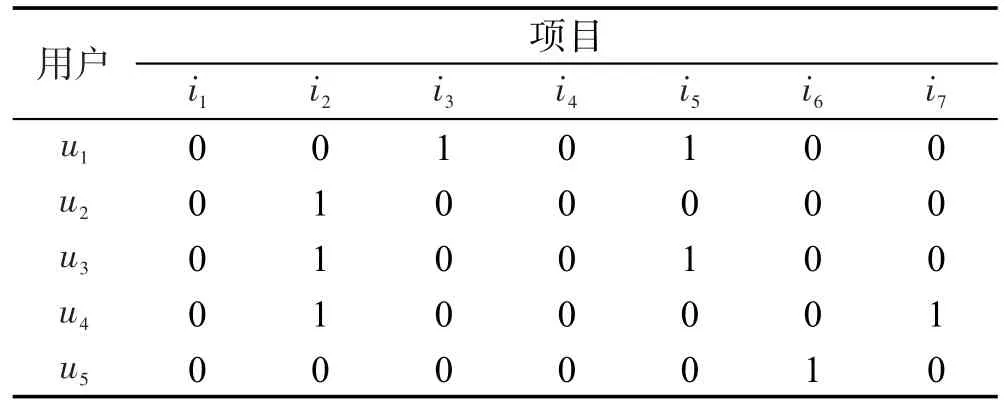
Table 3 User dislike item matrix表3 用户不喜欢的项目矩阵
表2和表3分别根据表4中的项目类型对应累加后形成的结果如表5和表6所示。
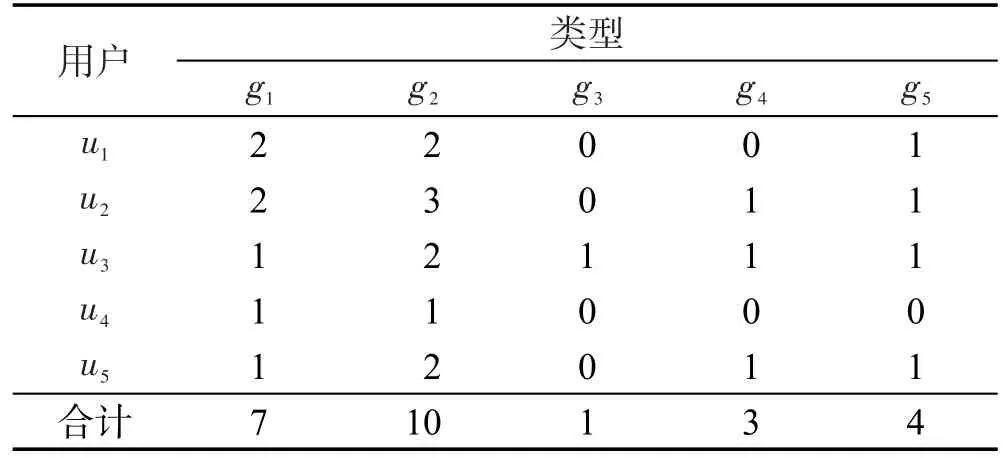
Table 5 Summary of user favorite item type表5 用户喜欢项目类型汇总
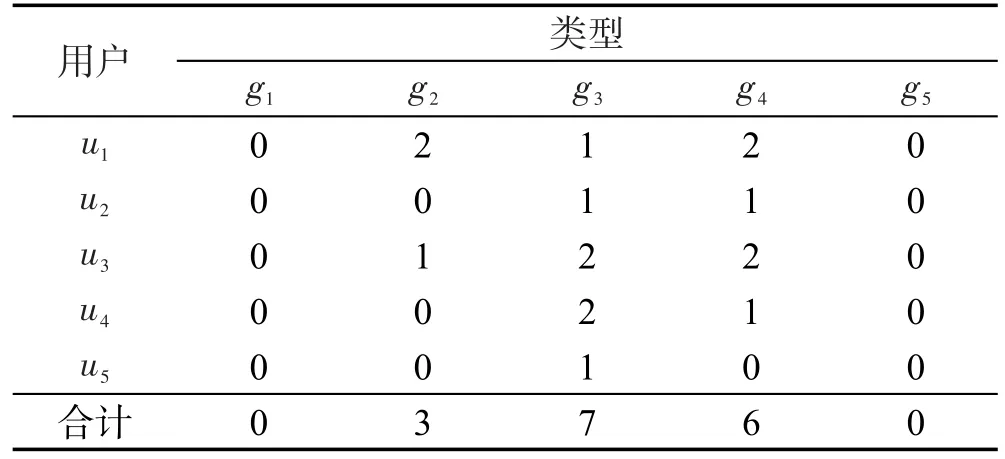
Table 6 Summary of user dislike item type表6 用户不喜欢项目类型汇总
从表5和表6中可知用户最喜欢的项目类型为g2,最不喜欢的项目类型为g3。那么这两个已筛选出来的类型所对应的项目纳入到最后预测评分的用户-项目矩阵中。
3.3 算法描述
根据上述思想,算法流程描述如下:
输入:用户-项目评分矩阵Rm×n,项目-类型矩阵Gn×s,目标用户u,待评分项目i。
输出:目标用户u对待评分项目i的预测评分。
步骤1利用矩阵Rm×n,使用常用的相似度计算方法计算出用户相似度LEsim(xu,xv),选取Top-K形成目标用户u的近邻用户集合Su,并根据Su形成相似用户-项目矩阵R1k×n。
步骤2利用矩阵Gn×s和Rm×n,根据本文所提出的项目类型相关性计算公式(9)计算出待评分项目i的类型与其他类型的相关程度,选取Top-K形成集合G1={g1,g2,…,gk}。
步骤3利用矩阵R1k×n,挖掘出目标用户u最喜欢的和最不喜欢的项目类型,组成集合G2={g1i,gdis}。
步骤4在矩阵R1k×n,剔除不属于G1∪G2的项目,形成局部数据比较密集的矩阵R2k×c。
步骤5利用矩阵R2k×c,根据加权Slope One算法计算出目标用户u对目标项目i的预测评分,产生Top-N推荐。
改进算法通过步骤1至步骤4的操作将大小为m×n原始用户-项目评分矩阵进行预处理,在预处理过程中根据项目类型相关性的计算选择Top-K个相关类型,并按照项目筛选策略形成局部数据比较密集的用户-项目评分矩阵R2k×c,k≪m且c≪n。这样可以在Slope One算法复杂度保持不变的情况下,通过大幅度降低输入数据规模的方法来提高算法的执行效率。虽然数据预处理部分会使整个算法的时间复杂度略有增加,但该部分可采用离线的方式处理,因而不会影响Slope One算法的实时性。
4 实验分析
4.1 实验数据集与评价标准
本文实验环境配置如下:OS Win 7,CPU i5-4460、3.20 GHz,内存2 GB或以上,硬盘空间50 GB以上。本文算法采用Java语言实现,使用了Apache Mahout开源框架下提供的原生Slope One算法,在此之前用本文算法对数据集进行了过滤筛选处理。
本文使用数据集MovieLens(http://files.grouplens.org/datasets/movielens/)中的部分数据来评估本文所提出的推荐算法的性能。选取的数据集包括用户数量为943、项目(电影)数为1682、用户-项目评分矩阵中包含100000条记录,其中每个注册用户要求至少完成20部电影的评分,给出的评分采用5个等级,即范围为{1,2,3,4,5},评分数值越大,则表示该用户对该项目越喜欢。该用户-项目评分矩阵的稀疏度为0.93695。
实验的评价指标:平均绝对误差(mean absolute error,MAE)和均方根误差(root mean squared error,RMSE)[14-15]。根据它们的值来验证本文所提算法预测结果的优势。
MAE计算如式(13)所示:

若将用户u表示为Uu,项目i表示为Ii,则在式(13)中,rui表示Uu对Ii的评分真实值,preui表示Uu对Ii评分的预测值。|T|表示测试集T中元素的个数。对于计算结果,MAE值越小,说明预测评分与实际评分越接近,预测结果就越准确。
RMSE计算如式(14)所示:
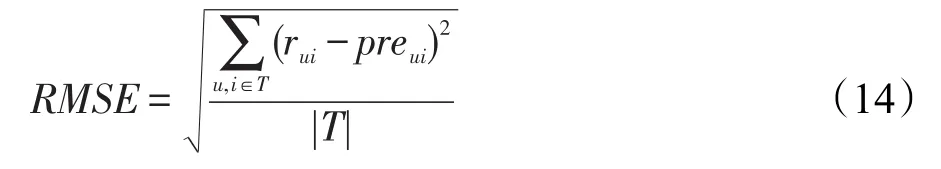
同理,RMSE值越小,表明算法预测值与评分真实值越接近,预测效果越好。
4.2 参数ω的最优值确定
参数ω表示式(9)中g_prob(a,b)和g_weight(a,b)所占权重的比例。使用基于项目的协同过滤算法进行实验,选取相似项目类型的数量为3,选取ω为不同值进行多次实验,得到使算法效果达到最好的参数值。比重参数ω对MAE值和RMSE值的影响如图1和图2所示。
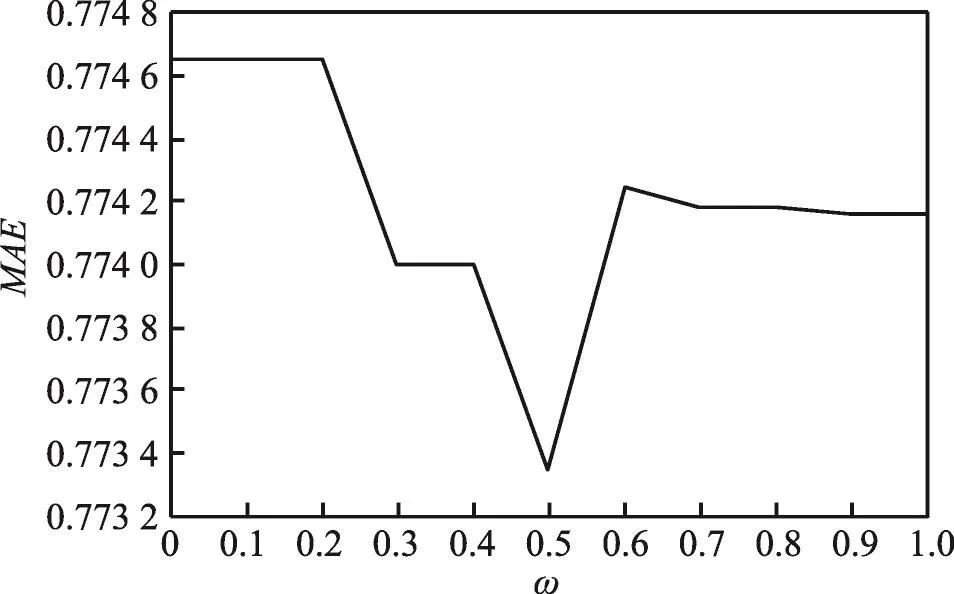
Fig.1 Effect of parameterωon MAE图1 参数ω对MAE值的影响
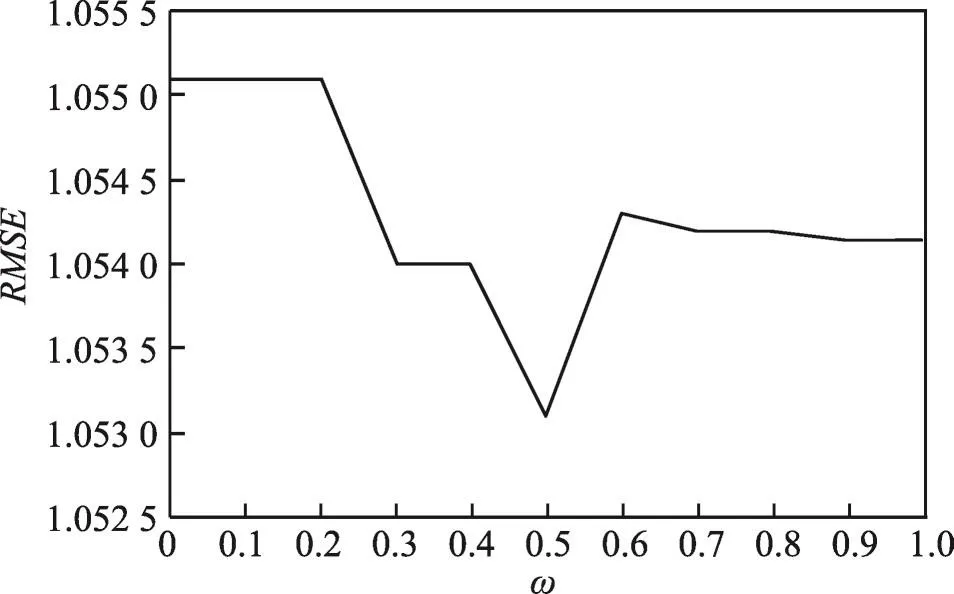
Fig.2 Effect of parameterωon RMSE图2 参数ω对RMSE值的影响
如图1、图2所示,经过多次实验,得出ω=0.5时式(9)的实验效果最好,因此本文实验中取ω为0.5。根据此实验结果,可以预先计算出系统中项目类型的相关性,表7计算出了MovieLens数据集中部分项目类型的相关性。
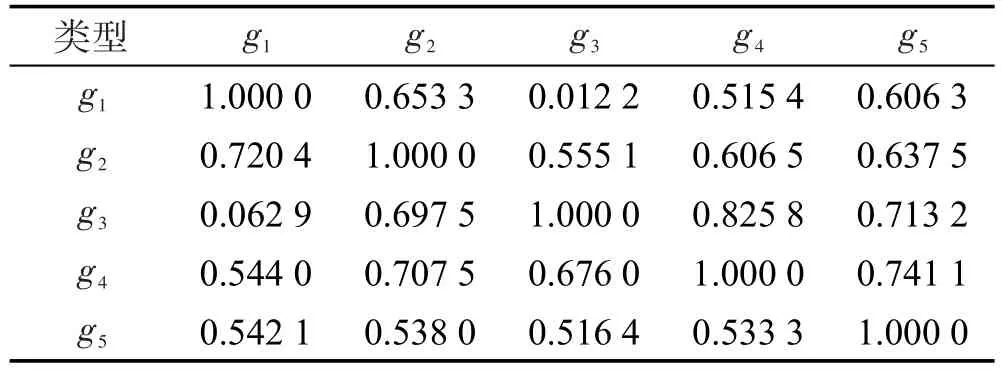
Table 7 Item relevance of MovieLens data set(part)表7 MovieLens数据集部分项目类型相关性
4.3 算法准确度对比实验
为了验证本文所提出算法具有较高的准确度,设置如下对比实验:在MovieLens数据集中,分别使用融合用户相似度和项目相似度的加权Slope One算法(简称算法1)[16]和基于用户多属性和兴趣的加权Slope One算法(简称算法2)[17]进行实验,根据实验运行的结果来计算MAE和RMSE的值。在实验过程中,选取当前目标用户的近邻用户集大小分别为5,10,20,…,160,进行多次实验,以排除偶然因素。3种推荐算法预测准确度的比较如图3和图4所示。
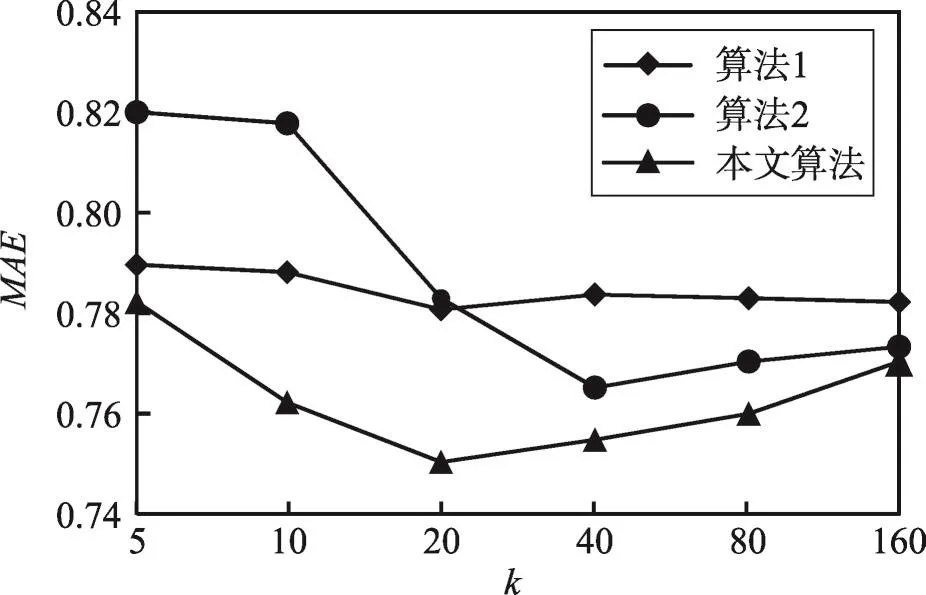
Fig.3 MAE contrast of 3 recommended algorithms图3 3种推荐算法运行结果MAE值对比
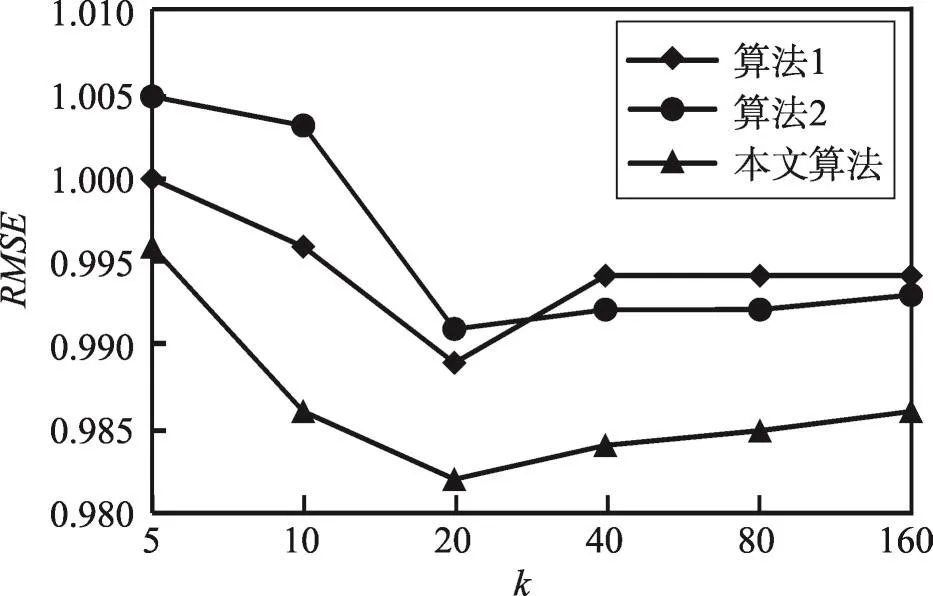
Fig.4 RMSE contrast of 3 recommended algorithms图4 3种推荐算法运行结果RMSE值对比
从图3、图4可以看出,本文算法在整体表现上优于算法1和算法2。本文算法MAE和RMSE值呈现先下降后上升趋势的原因:随着近邻用户集由5增至20的过程中,与目标用户相似的用户越来越多,因此预测准确度会提高,随着近邻用户集继续增加,并不是很相似的用户也被纳入其中,这就必然会导致预测准确度下降。
4.4 稀疏数据集中的性能对比实验
为了检验在不同稀疏程度的数据集下本文算法的预测性能,设置实验数据:在原始的MovieLens数据集(其稀疏度为0.93695)中删除部分数据,使其稀疏度达到0.99。将3种算法应用到该稀疏数据集中,预测准确度的比较如图5、图6所示。
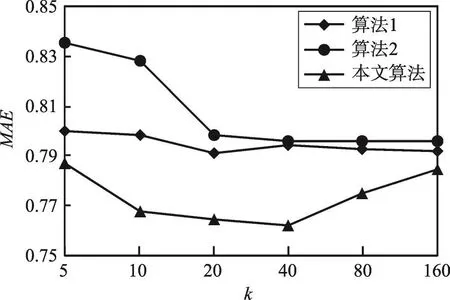
Fig.5 MAE contrast of 3 recommended algorithms(sparse data set)图5 3种算法在稀疏数据集上MAE值对比
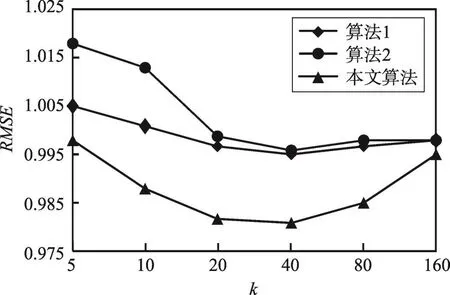
Fig.6 RMSE contrast of 3 recommended algorithms(sparse data set)图6 3种算法在稀疏数据集上RMSE值对比
根据图5、图6可以看出,在不同稀疏程度的数据集上,实验结果所呈现的整体趋势是一致的,每个算法在稀疏度较小的数据集上所得的MAE和RMSE值都要小,并且在稀疏程度较大的数据集上两种对比算法所呈现的差距变大,这说明本文算法在数据稀疏的情况下表现依旧良好。
5 结束语
本文针对加权Slope One算法中没有考虑项目相关性的不足,提出了在加权Slope One算法中融合项目类型相关性及项目筛选策略,给出了项目类型相关性的计算方法以及适应Slope One算法特点的项目筛选方案,排除了无关项目对推荐的干扰,并对算法的处理流程进行了改进。最后通过实验验证了本文算法在预测准确度、处理稀疏数据集等方面均有优势。随着网络互连的飞速发展,推荐算法中使用的用户数和项目数将呈指数增长,从而导致算法运行速度较慢,且过度耗费内存资源。未来可以考虑将一些优化性能较高的机器学习方法与本文改进的推荐算法相融合,在提高算法预测准确度的同时改善算法的时空效率。
