室内移动机器人人机交互的语义实现*
2018-10-12王恒升
王恒升,任 晋
1.中南大学 机电工程学院,长沙 410083
2.中南大学 高性能复杂制造国家重点实验室,长沙 410083
1 引言
对移动机器人进行远程控制是很多场合的不二选择。例如月球或火星探测车,用于灾害或危险场合的探测、作业或救援机器人等。对机器人进行远程操作的研究与实践很早就出现了,例如在美国三厘岛核电站发生核事故后,就使用了一台远程操作的机器人,操作人员在无核区,通过铅化玻璃,操作处于有核区的一台机器进行核事故处理[1]。
文献[2]提出一种通过自然语言进行远程人机交互的方案,即操作人员通过自然语言发出指令,机器人在远程执行指令要求的动作。这种自然的、类似人与人之间的交互方式不(或者很少)需要对操作人员进行专门训练。用于救灾机器人的交互时,方便领域专家直接对机器人发出紧急作业指令;用于服务机器人的交互时,更容易为普通用户所接受。
正如人与人之间进行语言交流时,人们对交流中所用的语言术语有着基本的共识,这是相互理解的基础。与机器人进行自然语言交互时,也需要对语义进行定义。目前语义网的研究对概念的语义定义采用本体(Ontology)的方式[3-8],即定义概念的类结构及相互关系,实现知识的表达与知识的检索获取。本文的研究目标是对机器人基于自然语言进行导航控制,要控制的机器人处于建筑物内部。因此导航用语中有大量的建筑物内部的地名词,例如“走到601房门口”,“在A座4楼电梯口往左拐”等,这里的“601房”、“A座”、“4楼电梯”等均是与某建筑相关联的地名词。本文借用本体的方法建立建筑物内部的地名词的概念体系,在此基础上建立建筑物的语义地图。
本文所说的语义地图,其实质是基于本体的对建筑物内部地名词的描述,更进一步说,是对建筑物空间知识的一种表达,或者说是关于建筑物内部空间的数据库。本文采用Prolog语言[9-11],将地名词描述为Horn Clause事实,其中包括名字信息、空间坐标信息等。从这些事实库中可以得到建筑物内部空间的拓扑连接关系(即拓扑地图)供机器人进行路径规划等,也能画出建筑内部空间简要的平面图供操作者参考。这样定义的地名词与人对这些名词的理解是一致的,也就是具有相同的“语义”;同时能够方便获得所需要的“地图”,本文称为语义地图。
语义地图是一种基于语义表达环境地理信息的一种方法,属于知识表达的范畴,在机器人人工智能领域有广泛的研究及应用预期。Zender等人[12]首先提出并实现了层级式的空间表达模型,应用于典型的室内办公环境,在尺度地图、导航地图、拓扑地图的基础上,通过激光、相机的传感信息来识别物体,借助自然语言处理,抽取出概念地图,以基于描述逻辑的本体语言的形式储存。Crespo等人[13]提出了一种语义关系模型,机器人通过人机对话系统完成室内环境下的高层导航任务,语义概念的相似性适应于不同环境。Tenorth等人[14]提出了一种处理知识的服务框架KnowRob,使用prolog语言,将模糊的任务描述与任务操作所需详细信息联系起来;其合作者Beetz等人[15]在此基础上,开发出一套功能更为完善的知识处理服务平台Open-EASE,可实时获取机器人的操作片段,并可以询问到机器人所观察和推理的信息,例如完成任务的方式、原因以及相关行为引发的后果。Drouilly等[16]和Landsiedel等[17]对室外更为复杂的语义地图进行了探索,描述了街道地图。本文的关注点在于室内环境的语义地图构建,主要目的是为移动机器人能够应用于室内环境、与人通过自然语言的方式进行交互。出发点是将建筑物环境信息作为先验知识和推理的基础,服务于人机交互;进一步基于传感器数据对室内空间和物体进行辨识,补充语义地图的动态信息,不在本文范围。
本文后面的内容安排如下:第2章以某实际大楼为例,介绍语义地图的构建;第3章利用“事实-规则-推理”的逻辑编程方法,在语义地图事实库的基础上,实现机器人自定位的逻辑程序设计;第4章通过逻辑编程实现机器人的自定位算法。
2 构建语义地图
2.1 建筑物简介
以中南大学机电工程学院大楼为例构建语义地图。该大楼是一个集办公、教学和实验于一体的综合建筑,以下简称CMEE,图1为其第四层平面图。CMEE包含4栋建筑,图1由左到右分别为A、B、C和D栋。这4栋建筑每层均由桥式走廊连通。A栋为办公区,共有6层。其他3栋为实验和教学区,共有5层,图2示出各楼栋楼层的高度(虚线框代表楼栋,粗实线代表楼栋各层的连接通道)。CMEE相对较为复杂,在楼层、建筑群、连接通道、室内功能空间等方面具有多样性和代表性,涉及语义丰富,对医院、商场、写字楼等类型的建筑均可有相似的语义表达,因此具有一定的代表性和可移植性。
2.2 建立本体
首先考虑描述建筑物空间的最小单元(基元),选择区域和节点两类最小单元。
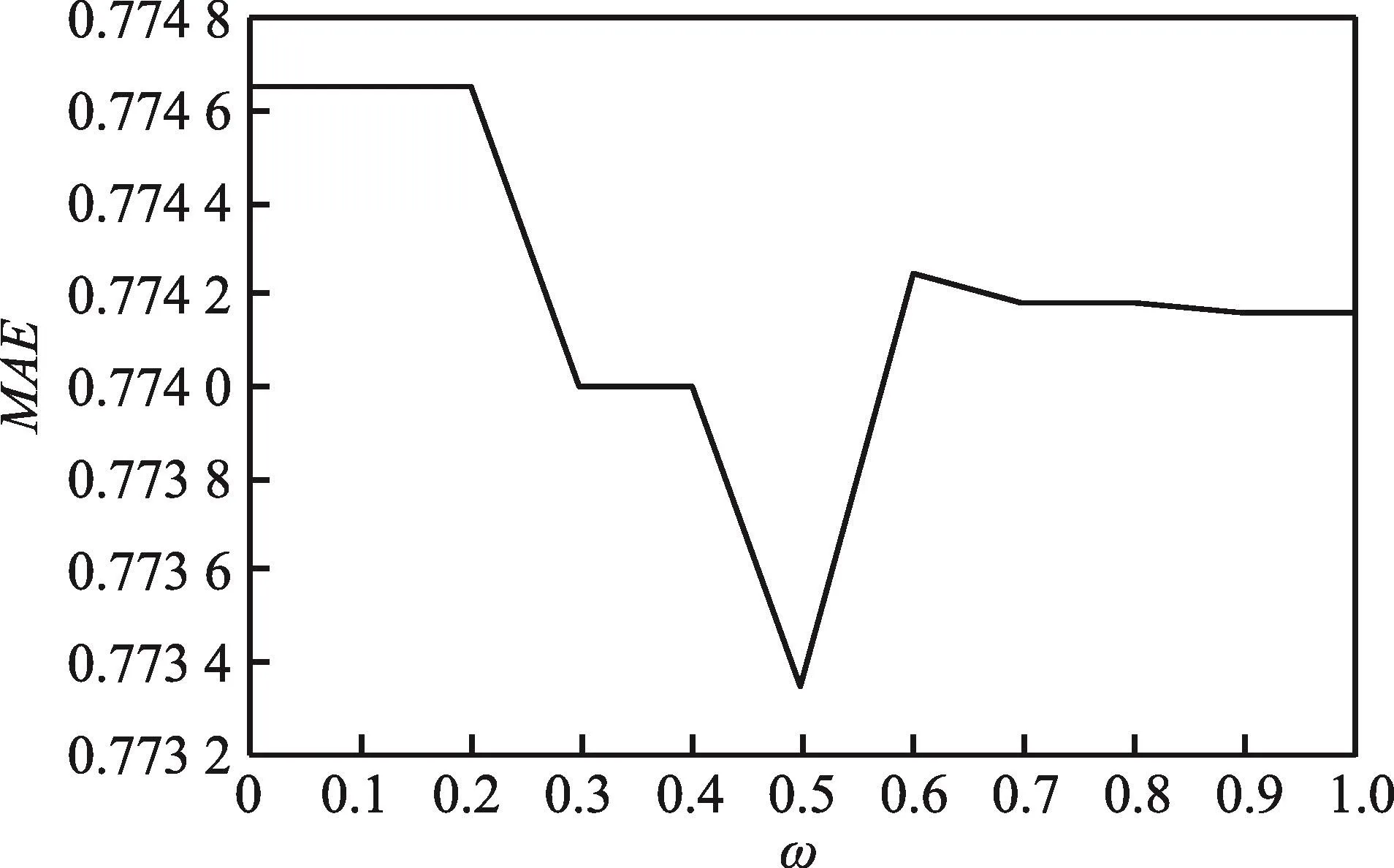
Fig.1 Fourth floor of CMEE图1 CMEE第四层平面示意图
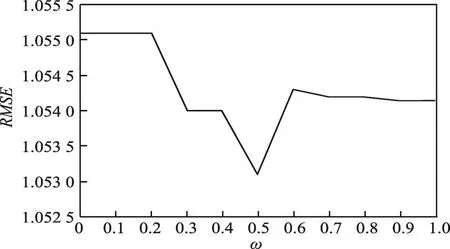
Fig.2 Diagram of floors height of CMEE图2 CMEE高度方向示意图
区域是指由墙壁分割开的空间,包括房间(使用空间)和交通空间[18]。交通空间分为水平交通空间和垂直交通空间。水平交通空间又分为楼道(楼栋内部通道)、桥式通道(连接楼栋与楼栋的通道)和台阶(连接室内局部高差)。垂直交通空间又分为楼梯间和电梯间。
节点指的是区域之间的连接点,例如房间的门就是房间区域与楼道区域的连接点,再如一个十字路口的交叉点也是一个节点(即两个或多个楼道的连接点,有时存在一个实际的防火门)。将节点定义为一个实体是方便建立区域之间的连接关系。
CMEE的概念本体如图3所示,从不同的视角进行分类,最终落实到最小的单元实体,即区域和节点。最小的单元实体可按不同的角度归属不同的类。例如一个房间a513,根据用途可归到办公室类,根据所处的楼层可归到5楼,根据所在的楼栋可归到A栋。
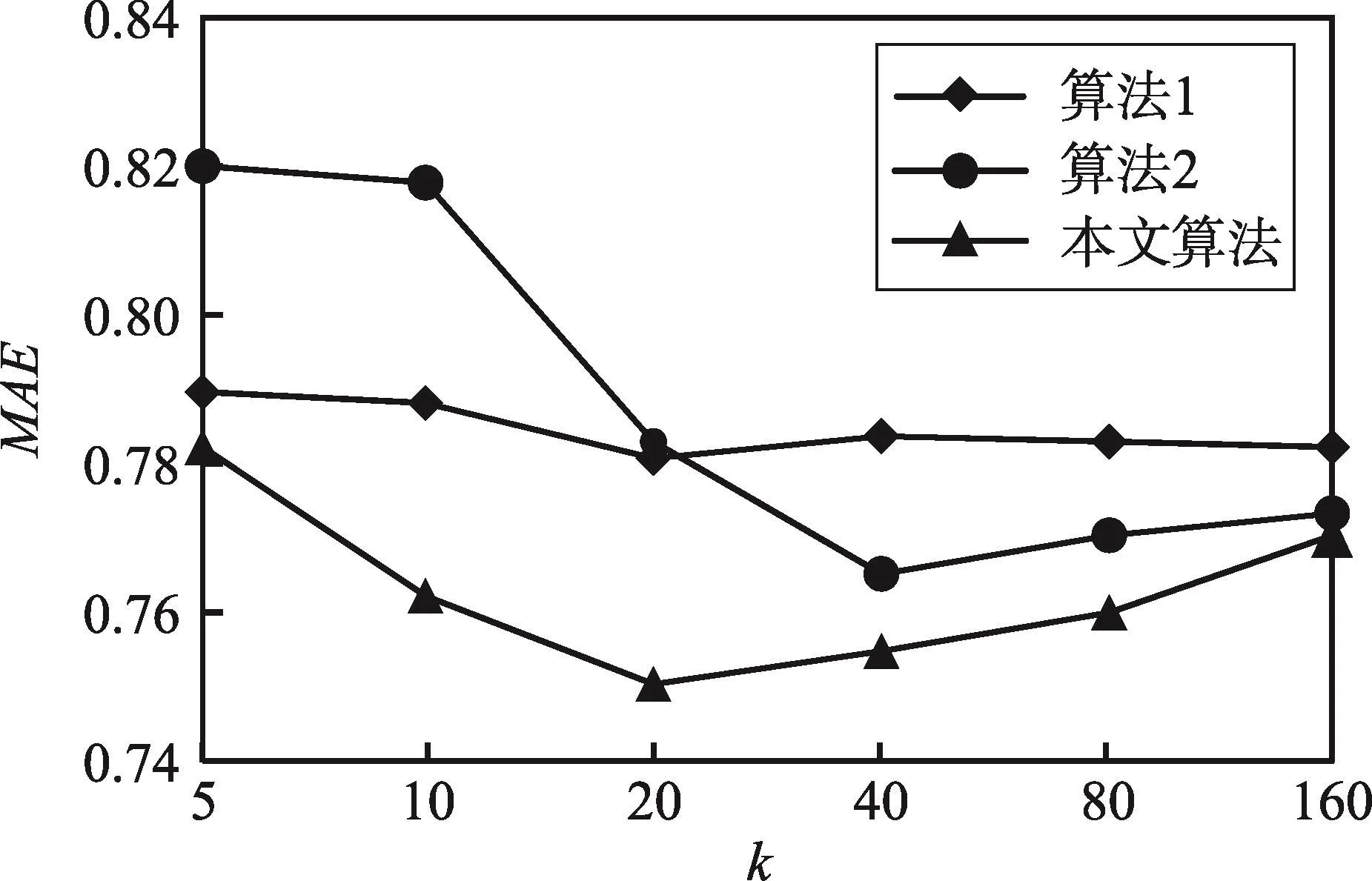
Fig.3 Ontology of CMEE图3 CMEE的概念本体
对最小单元实体按照日常用语习惯进行命名。例如房间编号“a601”,可以清楚看出该房间是位于A座6楼的01号房间。模仿房间命名格式,可以对具体的每一个楼道和台阶个体进行编号,如“a6c1”代表A座6楼,后面的字母c代表其区域类型为楼道(corridor),最后的数字1是该楼道的具体编号;对节点的命名也一样,如“a601d1”,代表a601房间的第一个门口(其中d代表门);再如“a6p02”,代表a座6楼的第二个交叉路口(其中p表示楼道连接的虚拟节点)。需要注意的是,建筑物内还存在若干区域无法用上述规则准确命名,如桥式走廊和楼梯间等,分别连接着相邻的楼栋与楼层。类似前文用单个字母的表达形式无法充分表明其真实的连接关系,因此引入双字符以准确命名。如区域“p4cd6”,其中,第一位字母p代表区域类型为桥式走廊(passage),第二位数字4代表位于4层,第三、四位代表连接C栋和D栋,第五位数字是该区域的具体编号。类似地,“s45a1”代表位于A栋、连接4层和5层的1号楼梯间(stairwell)区域;“e5a1”代表位于A栋5层的1号电梯(elevator)。其中,当楼梯间(或电梯)与各层区域连接的节点位于桥式走廊上,即处于楼栋与楼栋之间时,借助不同编号定义的桥式走廊,如图1所示的①~⑥,采用单个字母p(区别于a、b、c、d),配合对应桥式走廊的唯一编号准确定义。
2.3 语义地图描述
选用Prolog语言[9-11]进行语义地图的描述。Prolog是一种基于一阶谓词逻辑的描述型逻辑编程语言,是最早出现的逻辑编程语言之一,1972年在法国马赛由Colmerauer和Philippe Roussel共同开发,最早用于自然语言处理;迄今Prolog仍是应用最广的逻辑编程语言,有免费的和商用的多个版本,广泛应用于机器证明、专家系统等需要知识表达与逻辑推理的场合。随着新技术和新思想的出现,在Prolog的基础上扩充了许多功能,如约束逻辑编程(constrained logic programming,CLP)、面向对象逻辑编程(objectoriented logic programming,OOLP)、回答集编程(answer setprogramming,ASP)等,扩展了对语义网支持的Prolog形成了RDF、OWL描述语言。各种版本及扩展的逻辑编程语言,其基本描述方式和语法表达都是基于Prolog的。为阅读方便,本文的示例均以Prolog的语法给出,并在免费平台SWI-Prolog上调试通过。
用Prolog对CMEE的每个单元实体进行定义,就构成了语义地图的事实(facts)数据库,这样可以实现定义的完备性并避免重复定义。每一个单元实体事实包含两项基本内容:名字和坐标。根据Prolog的规范,小写字母开头的表示常量,描述事实的语句中所有量均为常量;大写字母开头的表示变量,在实现推理的谓词设计中,所有量均为需要绑定的变量。本文涉及Prolog程序的叙述均沿用这个惯例。本文的所有程序均在SWI-Prolog中调试通过。
例如一个区域实体a603的定义为:
area(a603,[coor(122660,110342,19600),coor(121859,112391,19600),coor(126610,114247,19600),coor(127920,110893,19600),coor(123169,109038,19600),coor(123024,109411,19600)])
其中第一项为区域的名称,后面的一个列表就是该区域的多边形顶点坐标序列。
再如节点实体a603d1的定义为:node(a603d1,coor(122842,109876,19600))。
其中定义式中的coor(122842,109876,19600)表示一个点的三维坐标,Prolog可以很方便实现这种自定义数据类型。
3 语义地图应用
有了基本的语义地图数据库,可以在Prolog的框架下设计各种谓词,实现不同的推理需求。
3.1 生成拓扑地图
拓扑地图从高一层次上反映了区域之间的连接关系,是实现最短路径规划的基础。生成拓扑地图的基础是建立区域和节点之间的连接关系。通过下面的谓词connect/4进行推理,可找到直接相连接的两个区域Area1和Area2。

谓词中的参数Node是连通两个区域的节点,Dis为两个区域之间的距离。这个推理描述的逻辑为:“如果节点Node既在区域Area1内,又在区域Area2内,且Area1和Area2不同,那么这两个区域通过该节点直接相连”。Prolog是一种描述性语言,其谓词设计的基本思想是按约束满足问题(constraint satisfaction problem,CSP)的思路将问题描述出来。例如上面的谓词connect(Area1,Area2,Node,Dis)就是寻找同时满足in_area(Node,Area1)(即Node在区域Area1中)、in_area(Node,Area2)(即Node在区域Area2中)和not(Area1==Area2)(即这两个区域不同)3个条件的变量Area1、Area2和Node;最后一个条件area_distance()不需要搜索,只是完成一个计算过程,即计算通过节点Node相连的两个区域Area1和Area2之间的距离。问题的求解是由Prolog来完成的。设计者的主要任务只是描述问题而不是像其他程序设计语言那样给出具体的求解过程。
有了上面的谓词后,可借助谓词save_fact/0,由CMEE的基本事实库生成一个扩展事实库directly_link.pl。

事实库directly_link.pl描述了CMEE的所有区域之间的直接相连的关系,实际上就是生成一个拓扑地图数据库。
3.2 扩充的概念语义
有了这些定义的基本单元实体后,可以通过基本规则来定义扩充的概念语义,如楼栋(building)、楼层(floor)等。这些语义是日常口语中常用到的。下面给出通过区域名称和当前位置坐标来判别楼栋和楼层的推理过程。
3.2.1 根据区域名称推理
若机器人观察到区域门牌号,或是从人机交互中获得空间区域的名称信息,则可以根据这些地名词和地名词的命名规则,推理出相应的楼层楼栋信息。
一个名为Name的实体属于“某栋”(Building)的基本规则可写为:

第一个字母
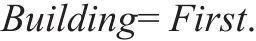
一个名为Name的实体属于“某层”(Floor)的基本规则可写为:
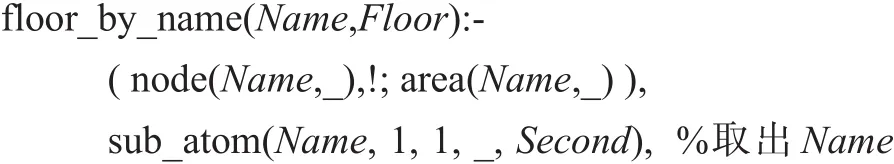
中的第二个字母
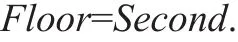
3.2.2 根据当前坐标推理
机器人也可根据自身实时位置坐标,推理出相应的楼层楼栋信息。下面的谓词building_by_coor/2实现这一功能。
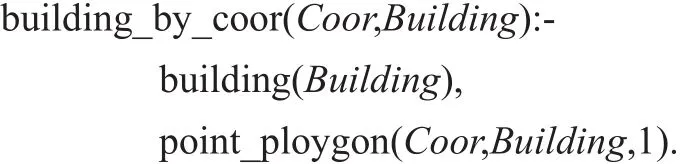
这里还用到了楼栋定义的事实,如A栋区域进行定义如下:
building(a).%区域a是楼栋
area(a,[coor(125300,117600,_),oor(97900,117600,_),coor(97900,45798,_),coor(107365,47528,_),coor(131465,53167,_),coor(148876,57241,_),coor(140363,79037,_),coor(141760,79583,_),coor(135211,96349,_),coor(133814,95804,_)]).%A栋的区域坐标信息
判断位置点与多边形关系的谓词point_ploygon/3是这里的核心,关于这个谓词的实现在后面第4章有详述。
通过下面的谓词floor_by_coor/2可以根据坐标推理出所在的楼层。

该谓词可判断当前位置处于A栋的各个楼层,其数据与图2中楼层高度是统一的。其他楼栋的楼层谓词也类似,这里省略以免冗长。
3.3 搜索最短路径
路径规划是移动机器人完成室内导航的基本任务之一。下面的谓词path/8可找出区域Area1到区域Area2的可行路径序列。

not(member(Area3,Pathlist1)),%保证新找到的区域不在已经过的区域序列中Dis3 isDis1+Dis2,
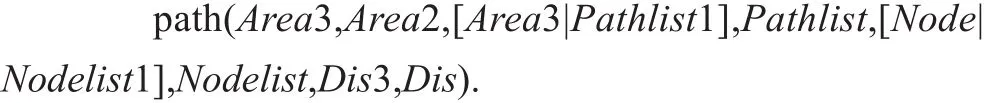
要找到连接起点Area1到终点Area2的一条路径,就先找到一个与起点Area1直接相连的区域Area3;将原始路径问题改为找到“起点是Area3,终点是Area2”的路径序列,如此用递归的方法最终可以解决原始问题。递归求解必须给出终止条件,如下。

当path/8中的两个区域直接相连,不再需要找到一个中间区域时,递归结束,得到满足条件的路径序列。
path/8中还用到其他约束条件,如not(member(Area3,Pathlist1))表示“中间区域Area3不在已经过的区域序列Pathlist1中”,确保“不走回头路”。该谓词同时还列出经过的节点序列和路径的路程长度。
谓词find_route/5从所有路径中找出路程长度最小的路径序列,由约束条件min(Dislist,Dis)来描述。若未找到答案,则返回空序列。

3.4 举例
为了方便说明,截取图1中CMEE第四层的局部区域,如图4所示。用2.3节的方法建立语义地图,用3.1节的方法生成形如“connect(c410,c4c3,c405d2,7276).”(表示房间c410和楼道c4c3通过节点c405d2相连,距离权值为7276 mm)的拓扑连接数据库(即拓扑地图)。为方便表达,将拓扑关系画在图5中。
Fig.4 Partial area of the fourth floor of CMEE图4 CMEE的第四层局部区域
Fig.5 Topological graph of Fig.4图5 图4所示区域的拓扑关系
在与机器人进行交互时,如需要从楼道c4c3到目的地c410,进行路径规划,可以发出询问“find_route(b4c2,c410,Pathlist,Nodelist,Dis).”。 由 3.3 节 的谓词find_route/5可以得到从楼道b4c2到房间c410的最短路径:区域序列为Pathlist=[b4c2,p4bc1,c4c3,c410],途径节点序列为Nodelist=[b4p01,c4p01,c405d2],总的距离和为Dis=66408 mm。最短路径在图5中用粗实线表示,可以看出,该最短路径是正确的。
4 点与多边形的位置关系
3.2 节中使用了一个谓词point_ploygon/3,用来判断点与多边形的位置关系。这个谓词在机器人的自定位中很有用。本章详细说明这一谓词的实现。
4.1 解决思路
点和多边形的位置关系是计算机图形学领域的基本问题[19-21]。常用的3种判断方法是:夹角和检验法、叉积判断法和射线法。其中,夹角和检验法需要进行大量复杂三角运算;叉积判断法只能判断凸多边形,不具备普适性,改进后计算量也不容忽视;射线法是从待判断点引一条射线,通过其与多边形交点数的奇偶性进行判断,是最常用的一种方法。
文献[22]基于射线法的基本原理,提出一种建立多边形顶点坐标数据库,然后利用数据库的SQL语言进行搜索。设计合适的搜索条件,可以得到点与多边形位置的判断结果。方法简便,运算效率高。本节的方法受这一思路的启发,将多边形表示为Prolog数据事实,然后利用Prolog的搜索及推理机制,实现点与多边形位置关系的判断。在具体实现上本节将待判断的点当作坐标原点,计算待判断多边形顶点的相对坐标;将点与多边形的位置关系转化为直角坐标系的正横轴与一系列边线段的相交关系。算法处理逻辑清晰,算法应用适合任何形式的多边形。
4.2 算法描述
将多边形平移到待判断点为原点的坐标系内,考虑任意边与正x轴的相交关系,遍历所有边,计算总的相交次数,可以得到点与多边形的关系:若交点总数为奇数,则被测点在多边形内;偶数,则在多边形外;在多边形上的情况需单独判断。如图6给出了所有可能的点与线段的相对关系。
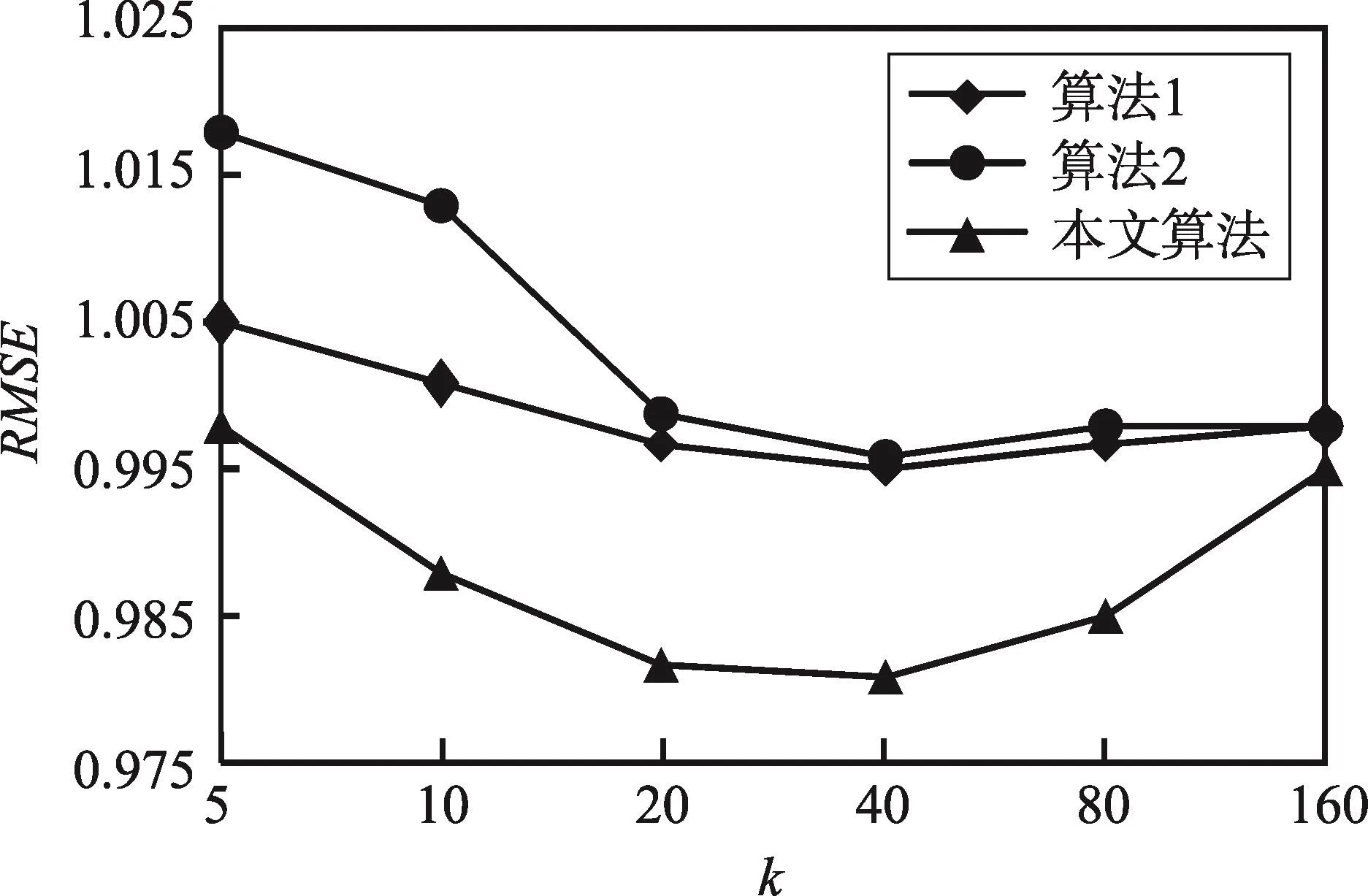
Fig.6 Positional relationship between point and lines图6 点与线段的位置关系
(1)图(a)表示线段在任一单独的象限内,与正x轴无交点。图(b)表示线段跨越1-2、2-3、3-4象限,无交点。图(c)表示线段跨越1-4象限,有交点。这3种情况比较容易判断,图中的ΔQ为线段端点所处象限的差的绝对值,根据这个值就可以对应这3种情况,进而确定交点情况。有一种特殊情况如图(d),将正y轴归于第一象限,负y轴归于第四象限,此时ΔQ=3与图(c)一样,但此时被测点处于线段上;为了区分这两种情况,增加“两端点横坐标均为0”的条件。
(2)图(e)和图(f)为 ΔQ=2的情况,即线段两端点位于相对象限。此时可能有一个交点,或者无交点,或者在线段上。具体情况可依据线段与x轴的交点来区分,交点坐标为:
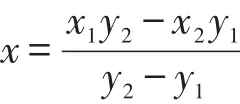
x>0时,线段与x正半轴有一个交点;x<0时,线段与x正半轴无交点;x=0时,被测点处于线段上。
(3)图(g)到图(i)涉及到被测线段有端点在x轴的情况。为了处理这种情况,特别将x轴负半轴上的点集定义为第八象限,将x轴正半轴上的点集定义为第十六象限。若ΔQ=8,则两端点分别位于x轴的正负半轴,如图(g)所示,点在线段上;若ΔQ=4,5,6,7,则一端点位于x轴负半轴上,如图(i)所示,线段与x正半轴无交点;若ΔQ=12,13,14,15,则一端点位于x轴正半轴上,如图(h)所示,线段与x正半轴有交点。参照文献[16]中给出的方法,根据走向给各交点赋不同的权值,比较两端点的纵坐标:
若y2>y1,走向向上,交点个数取值+0.5;
若y2 若y2=y1,走向水平,交点个数取值0。 表1总结了图6的所有情况,分为4类,其中0类和1类正好对应“0个交点”和“1个交点”的情况。其中符号0(1)表示类型0的第一种情况,2(3)表示类型2的第三种情况,以此类推。 Table 1 Classification of positional relationship between point and lines表1 点与线段位置关系分类情况 根据以上分析,判断待测点与多边形位置关系的算法描述如下: (1)将待测点设为原点,对多边形各顶点相对待判断点进行坐标平移变换。 (2)若存在一多边形顶点与原点重合,则待测点位于多边形上,跳至(9)。 (3)检测多边形一边线段与原点的关系,给出关系类型(如表1)。 (4)若其类型为2,则待测点位于多边形上,跳至(9)。 (5)若其类型为0、1、3,则原点与线段的交点数分别为0、1、0.5(或-0.5)。 (6)检查是否遍历完所有边。若无,则跳至(3)检测下一条边;若已遍历完成,则继续下一步。 (7)将点与遍历过的各边线段的交点数目求和。 (8)检测结果:若交点和为奇数,则点在多边形内;若为偶数,点在多边形外。 (9)结束。 以上算法可以用任何编程语言来实现,下面给出Prolog的程序实现,该程序充分利用Prolog的特点,结构清晰,运行效率高。设计谓词point_polygon/3,如下: point_polygon(Coor,Area,InOrOut):-%Coor为待测点,Area为多边形区域,InOrOut标志判断结果 area(Area,[Head1|Tail]), %匹配出多边形区域对应的顶点坐标序列 append([Head1|Tail],[Head1],List),%将坐标序列首项添加至序列尾部 coor_transform(Coor,List,NewList),%以待测点为原点,对坐标序列进行坐标变换 (member(coor(0,0,_),NewList),%判定点是否为多边形顶点 InOrOut=-1;%若是,给InOrOut赋值-1 intersection_number(NewList,0,N), %逐项判断原点与各新线段的位置关系及交点数,累加得出交点总数 round_mod(N,InOrOut)).%取整后判断交点数的奇偶性,输出InOrOut 上述算法预先将判断点和多变形顶点重合的情况剥离;原坐标点序列相对于待测点进行相对坐标转换后,得到新的坐标点序列和原点的相对位置关系,将线段端点的象限差作为分类依据进行判别。 为便于对比验证,采用文献[22]中的范例,并稍加改动,将全部可能产生特殊交点的情况考虑进去,以test命名测试区域,该区域事实为: area(test,[coor(240,22,_),coor(222,100,_),coor(347,31,_),coor(366,170,_),coor(302,226,_),coor(383,226,_),coor(337,352,_),coor(289,289,_),coor(185,289,_),coor(96,325,_),coor(182,170,_),coor(146,170,_),coor(80,200,_)]) 其中,谓词area的第二个参数即为区域test的有序坐标点序列,其二维平面图像如图7所示。坐标点序列亦可参照表2。 Fig.7 Example of polygon area图7 多边形实例 Table 2 Vertex coordinates of polygon in Fig.7表2 图7的多边形端点坐标 取10个有代表性的点进行验证(图7中用圆圈包围的数字),其中点①~⑤为文献[22]中的范例点,方便对比验证,⑥~⑩为随机抽取的任意点。待测点①~⑩的二维坐标分别为(216,64),(113,100),(200,170),(231,226),(158,289),(337,352),(103,260),(164.8,201),(247,135),(190,43)。程序运行结果:点①、③~⑤、⑨在多边形内部,点②、⑦、⑩在多外形外部,点⑥、⑧在多边形边上,符合实际情况。 针对前面第3章建立的语义地图,对移动机器人的定位算法和程序进行了真机实验。CMEE的语义地图数据库由各楼栋和楼层中的所有区域事实和节点事实构成,形如2.3节所述。全部的区域事实共665条,节点事实共924条。 在获取机器人实时的三维坐标后,借助3.2.2节所述谓词building_by_coor/2可推理出其所在楼层,机器人的自定位问题便由三维转化为二维平面问题。 例如,区域a420的事实为: area(a420,[coor(135475,45840,12800),coor(135621,46212,12800),coor(130870,48068,12800),coor(129560,44714,12800),coor(134311,42859,12800),coor(135111,44908,12800)]). 选取机器人所处3个位置:(1)节点a420d1(a420的1号门);(2)a421d1(a421的1号门);(3)a420内部任意一点node420n1。这3个位置的坐标: node(a420d1,coor(135293,45374,12800)) node(a421d1,coor(136603,48727,12800)) node(node420n1,coor(132794,45259,12800)) 算法point_polygon/3的运算结果与实际相符,即点a420d1、a421d1和node420n1与区域的位置关系分别为在多边形边上(InOrOut=-1)、在多边形外(InOr-Out=0)和在多边形内(InOrOut=1)。 机器人在建筑物内自定位时,需要判断机器人所在点的区域位置。依据前述建立的语义地图及扩展的语义数据库,引入层次渐进的搜索思路,先判断所在楼栋,再判断所在楼层,大大缩小了搜索范围。下面的谓词self_localization/2实现这一功能。 self_localization(Coor,Area):-%由坐标信息得到所在区域 building_by_coor(Coor,Building),%找到所在楼栋 floor_by_coor(Coor,Floor),%找到所在楼层 building_by_name(Area,Building),%匹配特定楼栋的区域 floor_by_name(Area,Floor),%匹配特定楼层区域 point_polygon(Coor,Area,1).%匹配所在的区域 移动机器人的智能在很大程度上取决于机器人对人类环境的理解,实现这一点的基础是机器人能够理解人类对其所处环境的名词概念,其实质就是建立有关环境的知识库。本文的工作以人用自然语言的方式,以对处于室内的远程机器人的导航控制为背景,要求机器人能够理解自然语言指令中的术语。以中南大学机电工程学院大楼为例,基于本体论建立了其室内地名词概念本体,用Prolog逻辑编程语言将该概念本体表述为其室内环境的知识库事实。Prolog逻辑推理功能的实现就是设计逻辑谓词,逻辑谓词的设计过程就是将其表述为约束满足问题(CSP)的过程。本文设计的Prolog谓词成功地用于建立语义地图、机器人自定位、路径规划等机器人导航所需的基本任务。所有的程序均在SWI-Prolog环境下调试通过,程序运行结果符合预期。这里给出的是研究救灾机器人人机交互的一部分,其他相关的工作包括自然语言理解、自然语言对话系统、机器人人机交互软件平台等,各方面的研究还在继续。本文作为机器人基于本体概念体系的逻辑推理实例,如自定位,是基于逻辑实现的,即在假设传感数据准确的条件下实现的,未涉及基于实体机器人的传感数据采集等内容。在机器人真机的现场实验方面,文中的程序及算法均运行正常,但由于机器人的里程计等传感数据及其处理在实际应用中还存在不少问题,作为机器人系统的整体导航效果还不够理想,这也是学术界正在研究的一个热点问题。
4.3 算法的Prolog实现
4.4 实例验证
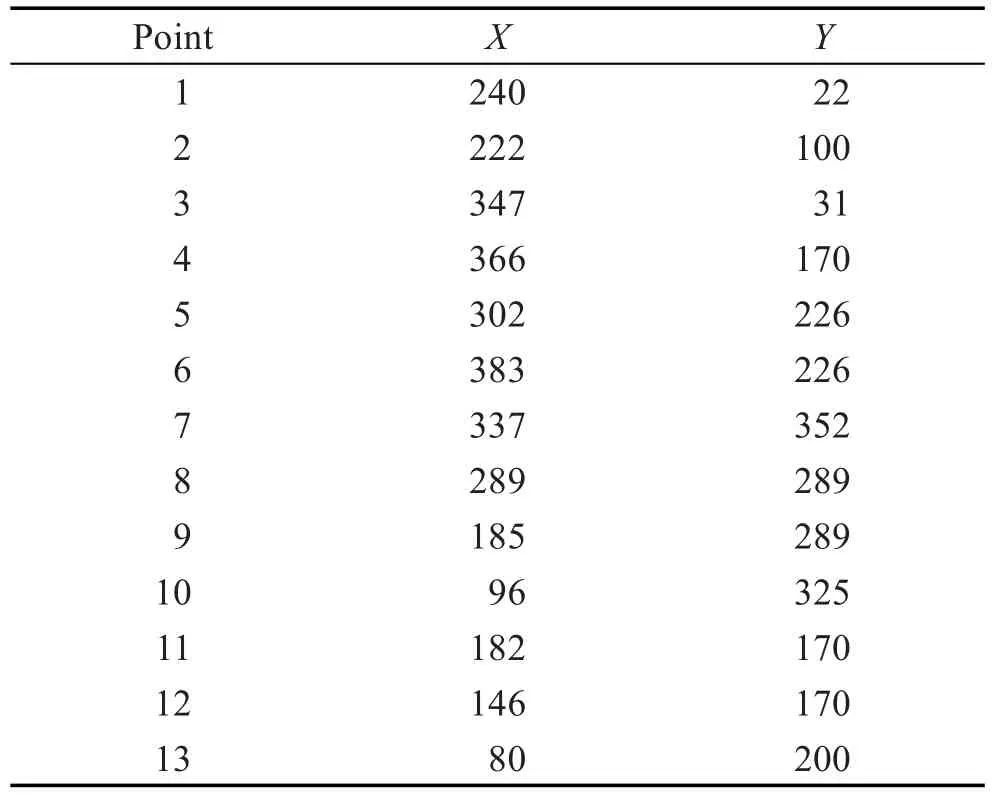
4.5 层次渐进的自定位算法
5 结论
