内埋弹舱典型结构振动响应分析与试验验证

沈重，王虎寅，赵斌，陈忠明

（沈阳飞机设计研究所，沈阳 110035）

高隐身飞机均采用内埋式弹舱结构，因此在超音速及跨音速下打开武器舱门时，不稳定气流进入弹舱内，在舱内前后产生膨胀波和压缩波，这种膨胀波和压缩波诱导结构产生强烈振动[1-2]。在该环境下，结构极易产生疲劳破坏，影响飞机飞行安全。

内埋弹舱振动、噪声特性研究始于针对空腔的流动激励研究。早期，针对空腔振动、噪声研究只限于风洞试验方法。1964年，Rossiter[3]首先对亚、跨声速条件下的空腔流动机理进行了大量的试验研究。通过显示技术，Rossiter发现了空腔周围的脱落涡和压力波，并推导出用于估算空腔流动自持振荡频率的半经验公式。后续众多学者[4-6]对空腔噪声进行了详细的研究，完善了空腔流动理论。

通过Rossiter半经验公式可知，弹舱后部结构，特别是后壁板所处的环境最为恶劣，因此，文中针对内埋弹舱后壁板典型结构形式进行了振动响应分析，并与振动试验进行了对比。结果表明，内埋弹舱采用的加筋结构形式合理，有限元计算结果能够满足动强度在工程上的计算精度要求。

1 试验

内埋弹舱的典型结构如图 1所示，采用加筋板结构形式，长约377 mm，宽约400 mm，高约25 mm，结构材料为抗疲劳性能较的 7050铝合金。利用MSC.PATRAN对该结构进行有限元建模，壁板及筋条采用 shell单元模拟，共有 8389个 shell单元，8507个节点，边界采用固支模拟，有限元模型如图2所示。

2 动力学分析

2.1 模态分析

利用 MSC.NASTRAN SOL103模块对该结构进行模态分析，可得前三阶固有频率为493、652、784 Hz，第一阶振型如图3所示。

2.2 随机响应分析

随机振动响应分析是由系统输入的统计特性计算系统输出的统计特性，研究的基本问题是由输入的自相关函数或功率谱密度函数来确定系统输出的自相关函数或功率谱密度函数，从而确定系统响应的方差和均方差。结构动力学方程为[7]：

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵。若初始速度和位移为0，则系统响应只由随机激励引起，求杜哈梅（Duhamel）积分得到时域响应，也可用积分变换得到频域响应：

式中：h(t)为脉冲响应函数；H(ω)为频率响应函数，与h(t)为一对傅里叶变换对。

计算所用的振动载荷谱如图4所示，得到各位置的加速度响应及应力响应结果，用于指导后续试验中传感器布置及结果对比。

3 试验验证

3.1 测点布置

根据随机响应计算结构，确定了振动试验时的加速度及应变的测点位置，如图5、图6所示，共两件试验件。

3.2 扫频结果对比分析

对两件试验件进行正弦扫频试验，1号试验件第一阶峰值频率约为509 Hz，2号试验件第一阶峰值频率约为495 Hz。根据模态分析结果可知，有限元计算的第一阶频率与试验扫频结果较为接近，因此，有限元模型及边界条件模拟较为准确。

3.3 加速度测试结果对比分析

对两件试验件按振动谱进行随机振动试验，振动控制谱精度满足国军标要求，试验结果与有限元计算结果见表 1。可以看出，1号点、3号点的有限元计算得到的加速度响应与试验结果较为接近，2号点与试验结果相差较大，误差为23.2%，基本满足工程计算结果要求。

3.4 应变测试结果对比分析

应力测试结果与计算结果对比见表 2。从表 2可以看出，应力计算结果与试验测试结果存在一定误差。主要是由于有限元模型建模过程中进行了简化，去除了倒角等细节信息，此外各阶的模态阻尼无法在有限元模型中准确地模拟导致计算误差。在各应变测试点中，3号测点的计算结果与试验测试结果误差最大，为-39.1%，其他测点二者误差大多在20%以下。两件试验件平均误差基本在 20%以下，表明有限元计算结果能够满足动强度在工程上的计算精度要求。

表1 加速度测试结果与计算分析结果对比表

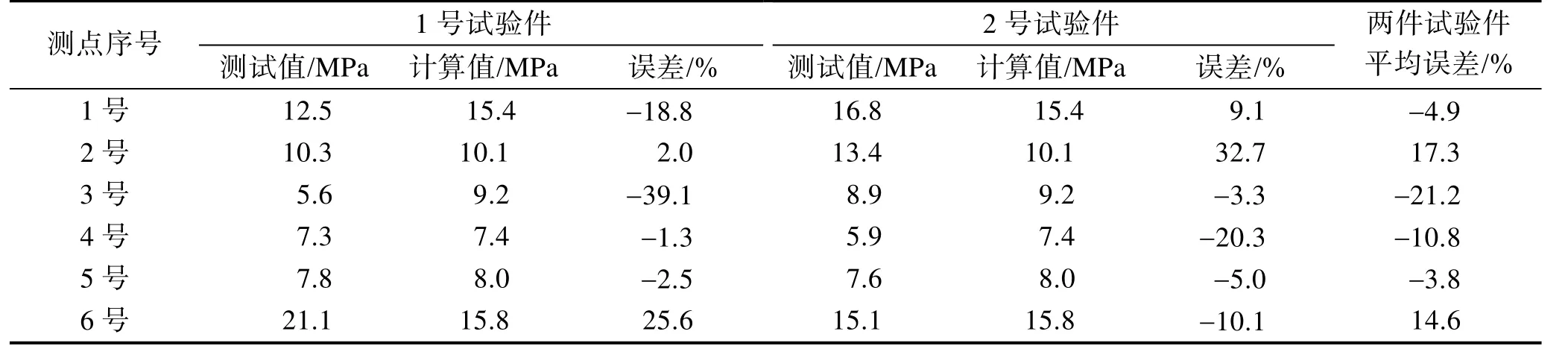
表2 应力测试结果与计算分析结果对比表

4 结论

文中通过对内埋弹舱典型结构进行振动试验及有限元分析，可以得到以下结论：

1）内埋弹舱典型结构试验件在本次试验规定的振动载荷和试验条件下完成了试验，试验件未发现工程目视可检裂纹等破坏现象，达到了规定的抗振能力，表明内埋弹舱选择该种加筋结构形式合理，满足动强度设计要求。

2）通过对有限元计算结果与测试结果对比可知，有限元计算结果能够满足动强度在工程上的计算精度要求。